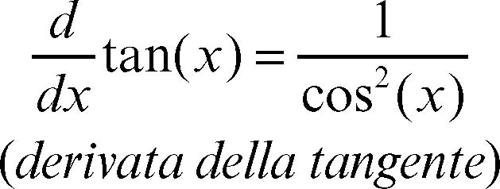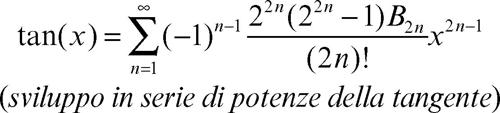tangente trigonometrica
tangente trigonometrica
tangente trigonometrica di un angolo acuto α di un triangolo rettangolo, è il rapporto, indicato con il simbolo tan(α) o anche tg(α), tra il cateto opposto e il cateto adiacente ad α: essa coincide quindi con il rapporto tra il seno e il coseno dell’angolo stesso. Tale definizione può essere estesa ad angoli arbitrari, considerando la retta tangente alla circonferenza goniometrica nel punto A(1, 0), e da ciò deriva il suo nome (→ funzione goniometrica). Si definisce così una funzione di variabile reale, la funzione tangente:
Nel piano cartesiano, il coefficiente angolare m di una retta di equazione y = mx + q è la tangente trigonometrica dell’angolo che la retta forma con l’asse delle ascisse.
La funzione tangente è una funzione dispari, periodica (di periodo π) e illimitata, con asintoti verticali in ogni punto x = (2k + 1)π/2, con k intero; negli altri punti essa è continua, derivabile infinite volte e la sua derivata è
La funzione tangente è analitica nell’intervallo (−π/2, π/2), cioè coincide con il suo sviluppo in serie di potenze; in tale intervallo vale pertanto:
dove Bk indica il k-esimo numero di → Bernoulli.
Valgono le seguenti formule:
(formula di addizione)
(formula di sottrazione)
(formula di duplicazione)
(formula di bisezione)
(formula parametrica)
TANGENTE TRIGONOMETRICA