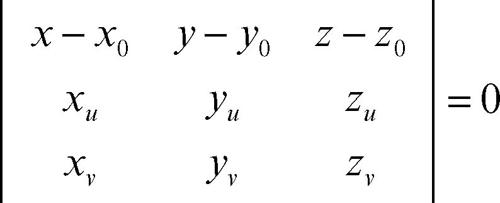tangente

Enciclopedia della Matematica (2013)

tangente


tangente termine usato in matematica con significati diversi.

☐ In geometria, la tangente a una curva è una retta che interseca la curva in un punto in cui vengono a coincidere almeno due intersezioni. La tangente t a una curva γ, in un suo punto P, è la posizione limite che assume una retta secante r passante per P e per un altro punto Q della curva, al tendere di Q a P. Nel caso particolare della circonferenza, la sua tangente in un punto P è perpendicolare al suo raggio avente un estremo in P. Se la curva è piana e rappresentata in un riferimento cartesiano Oxy, con lo stesso termine tangente è a volte indicato il segmento che ha per estremi il punto di tangenza e il punto in cui la retta tangente in esso interseca l’asse delle ascisse, mentre la proiezione sull’asse delle ascisse di tale segmento è detta sottotangente. Nel caso tridimensionale, le tangenti a una superficie in un suo punto P sono le rette tangenti a una qualsiasi curva della superficie stessa passante per P; esse formano il cono tangente alla superficie in P, che è un piano tangente alla superficie nel caso in cui le tangenti siano complanari (→ superficie).

☐ Dal punto di vista dell’analisi matematica, la tangente a una curva nel piano (o nello spazio) è una retta che ha un contatto del primo ordine con la curva stessa (→ contatto tra due curve), cioè che ha in comune con essa un punto e la sua derivata (rispettivamente, il suo vettore derivato). Nel caso di curva piana, se questa è esprimibile con un’equazione del tipo y = ƒ(x), essendo ƒ una funzione derivabile, la tangente a essa in un suo punto P0(x0, y0) è la retta per P0 avente coefficiente angolare uguale alla derivata della funzione in quel punto. La sua equazione è (y − y0) − ƒ′ (x0)(x − x0) = 0, essendo ƒ′ (x0) la derivata di ƒ calcolata in x0. Corrisponde, quindi, al polinomio di → Taylor di primo grado avente centro nel punto dato x0. Se la curva è scritta nella forma implicita ƒ(x, y) = 0, la tangente ha equazione ƒx(x0, y0)(x − x0) + ƒy(x0, y0)(y − y0) = 0.

In un punto di una curva avente molteplicità s passano, contate con la loro molteplicità, esattamente s tangenti aventi con la curva un contatto di ordine maggiore di s.

Analoghe considerazioni valgono per una curva sghemba. Se la curva è data nella forma parametrica x = x(t), y = y(t), z = z(t), la tangente in corrispondenza del punto t0 ha equazioni parametriche x(τ) = x0 + x′ (t0)τ, y(τ) = y0 + y′ (t0)τ, z(τ) = z0 + z′ (t0)τ. Nell’ordinario spazio tridimensionale la tangente a una superficie S in un suo punto P0(x0, y0, z0) è qualsiasi retta tangente a una linea regolare passante per P0. Se la superficie è regolare (per esempio di classe C 1), tutte le tangenti giacciono nello stesso piano, detto piano tangente. Esso ha le seguenti equazioni:

• se S è scritta nella forma cartesiana z = ƒ(x, y), il piano ha equazione

formula

• se S è scritta nella forma implicita ƒ(x, y, z) = 0, il piano è dato da

formula

• se S è nella forma parametrica x = x(u, v), y = y(u, v), z = z(u, v), il piano ha equazione

formula

le derivate parziali essendo naturalmente calcolate nel punto di tangenza.

Tra le tangenti a una superficie in un punto (semplice ordinario) ne esistono due (reali, distinte o coincidenti, oppure immaginarie) aventi con essa un contatto almeno del secondo ordine nel punto stesso; tali rette sono dette tangenti asintotiche. Nella involuzione in cui si corrispondono due tangenti che separano armonicamente le tangenti asintotiche (→ rapporto armonico) esistono due rette coniugate ortogonali, dette tangenti principali (bisettrici degli angoli formati dalle tangenti asintotiche); le tangenti principali sono infinite se l’involuzione è circolare (il punto è un → ombelico della superficie).

☐ Per altri significati, si veda → tangente iperbolica, → tangente trigonometrica.

P : fig_lettT_00170_001.jpg>

Vedi anche
applicazione Matematica Il concetto di a. è una generalizzazione del concetto classico di funzione (➔ corrispondenza). Si parla di a. di un insieme P in un insieme Q, quando tra i due si stabilisce una corrispondenza del tipo seguente: a ogni elemento di P corrisponde un ben determinato elemento di Q, mentre un elemento ... parabola neiloide In matematica, parabola di equazione y2=px3 (con p costante). approssimazione In matematica, si chiamano metodi, o procedimenti di a. o, semplicemente, a., procedure alle quali si ricorre per rappresentare enti matematici (numeri, misure, funzioni ecc.) in modo non esatto, ma sufficientemente accurato per gli scopi perseguiti, in genere mediante enti più semplici. Così, per es., ... cinematica Parte della meccanica, talvolta detta anche geometria del movimento, in cui si analizzano i movimenti indipendentemente dalle cause che li provocano e mantengono. A seconda che il corpo in movimento si rappresenti come punto materiale, come sistema rigido, come sistema deformabile ecc., si ha una c. ...
Tag
Altri risultati per tangente
  • tangente
    Enciclopedia on line
    In geometria, si dice di ente (retta, linea, superficie ecc.) che abbia un particolare rapporto spaziale con altro ente della stessa natura, definito caso per caso e che riguarda comunque l’intersezione dei due enti considerati (che si dicono anche tra loro t.). In particolare, retta t. a una curva ...
Vocabolario
madre di tutte le tangenti
madre di tutte le tangenti loc. s.le f. La tangente più cospicua, quella che ha permesso di scoprire un sistema di corruzione diffusa. ◆ La «madre di tutte le tangenti» sarebbe stata versata a vari intermediari d’affari e a ditte fantasma...
tangènte¹
tangente1 tangènte1 agg. e s. f. [dal lat. tangens -entis, part. pres. di tangĕre «toccare»]. – 1. agg. In geometria, di ente (retta, linea, piano, superficie, ecc.) che abbia un particolare comportamento con altro ente, definito caso per...