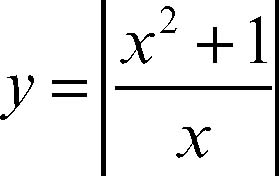tangenza all'infinito

tangenza all'infinito

tangenza all’infinito espressione intuitiva che equivale ad affermare l’esistenza di un asintoto. Per indicare che il grafico di una funzione y = ƒ(x) ha la retta r come asintoto (orizzontale, verticale, obliquo) si può anche dire che r è tangente all’infinito a tale grafico. Per esempio, il grafico della funzione y = 1/x ha come asintoto orizzontale l’asse delle ascisse perché

e quindi l’asse delle ascisse è tangente all’infinito al suo grafico. Il grafico di una funzione può avere anche più di un asintoto. Per esempio, il grafico della funzione precedente è anche tangente all’infinito all’asse delle ordinate, e quindi presenta un asintoto verticale, in quanto è

Il grafico di una funzione può presentare un asintoto obliquo destro, cioè per x → +∞ e un asintoto obliquo sinistro (per x → −∞) come nel caso della funzione

oppure un asintoto orizzontale destro e uno sinistro, come nel caso della funzione y = arctan(x). Tuttavia, proprio per la sua univocità, non può presentare più di un asintoto obliquo destro (sinistro) o di un asintoto orizzontale destro (sinistro). Non esiste invece un limite superiore per il numero di asintoti verticali che il suo grafico può avere: si veda per esempio la funzione y = tan(x), il cui grafico ha infatti infiniti asintoti verticali.