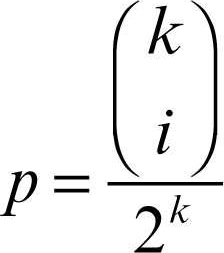Galton, tavola di
Galton, tavola di
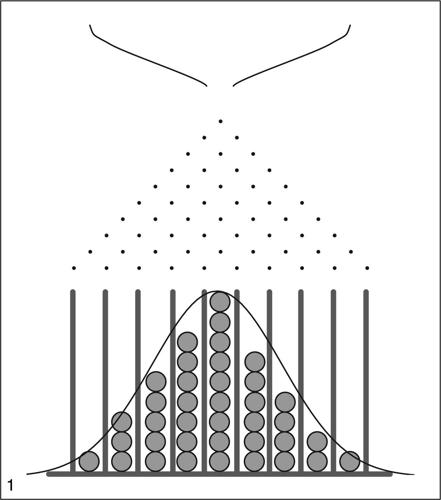
Galton, tavola di in probabilità e statistica, strumento didattico per mostrare come si forma una distribuzione binomiale. La macchina, ideata da F. Galton, è una scatola rettangolare alla cui base sono fissati dei chiodi disposti a triangolo, contenente delle palline nella parte superiore. Mettendo la scatola in posizione verticale le palline scendono oltrepassando casualmente ogni chiodo incontrato o a destra o a sinistra (e se la scatola è ben fatta ogni volta con probabilità 1/2). Le palline si depositano così sul fondo della scatola disponendosi secondo un andamento che approssima la curva normale. La tavola di Galton, oltre a mostrare come si produce un’approssimazione discreta della curva normale, ne spiega la genesi e chiarisce il motivo per cui la si incontra così frequentemente: la distribuzione è infatti il risultato di tanti piccoli errori in eccesso o in difetto rispetto al percorso principale. Senza errori (senza cioè le deviazioni provocate dai chiodi) le palline si accumulerebbero tutte nella colonna centrale. Se si indicano con 0, ..., n le successive file dei chiodi e se si numerano da 0 a k i chiodi della fila k, allora la probabilità p che una pallina incontri il chiodo i della fila k è
Per la particolare disposizione dei chiodi, essa è anche chiamata quinconce, dal latino quincunx, termine che indica cinque once e, più in generale, la configurazione di cinque oggetti distribuiti come sulla faccia di un dado.
