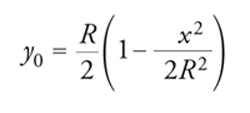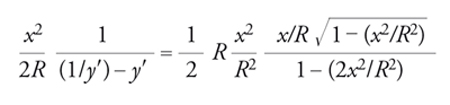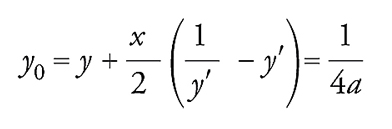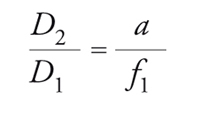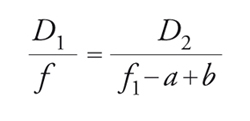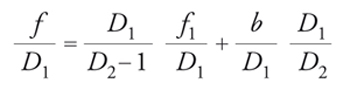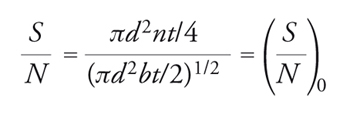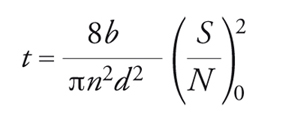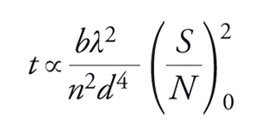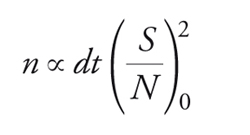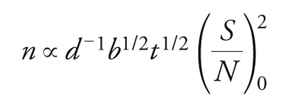Telescopi

Telescopi

I primi telescopi furono impiegati per finalità scientifiche sul finire del primo decennio del Seicento; gli sviluppi successivi mirarono a ottenere una maggiore luminosità, mediante la costruzione di lenti più grandi, e una migliore scala angolare, con l'aumento della lunghezza focale. Il principale problema ottico sorgeva dagli effetti cromatici, a causa della variazione dell'indice di rifrazione del materiale delle lenti in funzione della lunghezza d'onda. Inoltre, al crescere delle dimensioni delle lenti, cominciarono a manifestarsi notevoli problemi di flessione meccanica causata dalla gravità, che limitarono a 1 m il diametro massimo dei telescopi a rifrazione (o diottrici). Questi due problemi sono risolti dai telescopi a riflessione (o catottrici): in essi non vi sono effetti cromatici e, mediante supporti appropriati sul retro dello specchio, le flessioni possono essere in gran parte eliminate. Comunque, un prezzo va pagato: le superfici riflettenti tendono ad avere maggiori perdite di luce rispetto alle lenti e, dal momento che quasi sempre vi è uno specchio secondario sul cammino del raggio di luce incidente, gli effetti di diffrazione peggiorano l'immagine finale.

I telescopi astronomici devono essere in grado di seguire i corpi celesti che, in conseguenza della rotazione terrestre, descrivono circonferenze attorno ai poli. A tale scopo è stata realizzata la montatura equatoriale, nella quale il telescopio ruota attorno a un asse puntato verso il polo. La struttura asimmetrica che ne risulta è squilibrata e nei grandi telescopi comporta seri problemi di flessione. Una struttura più semplice è la montatura altazimutale, nella quale il telescopio ruota intorno a un asse orizzontale e a uno verticale. Quando il telescopio viene puntato in direzioni differenti, anche lo specchio subisce una deformazione causata dalle forze gravitazionali. In passato tale problema era risolto con specchi abbastanza rigidi che, se sostenuti da sistemi di leve meccaniche, non si deformavano troppo. L'avvento di strutture e sostegni controllati dal calcolatore ha reso possibile l'uso di specchi molto più sottili.

Diversi fattori ambientali possono pregiudicare il buon funzionamento di un telescopio. L'indice di rifrazione dell'aria dipende dalla temperatura e quindi, se lo specchio è più caldo dell'ambiente circostante, la convezione che ne deriva comporta un deterioramento della qualità dell'immagine prodotta. Vanno inoltre considerati gli effetti dell'atmosfera terrestre, in particolare quello della turbolenza. Anche nei siti migliori, gli effetti atmosferici limitano gravemente la qualità dell'immagine, tanto che un'immagine puntiforme (una stella) appare come una macchia diffusa con un diametro, a metà potenza, di mezzo secondo d'arco o anche più. Per correggere le immagini di oggetti astronomici alterate dagli effetti atmosferici, attualmente si stanno sviluppando varie tecniche che utilizzano stelle di riferimento naturali o artificiali.

Tipi di telescopi

Telescopi a primo fuoco

fig. 2

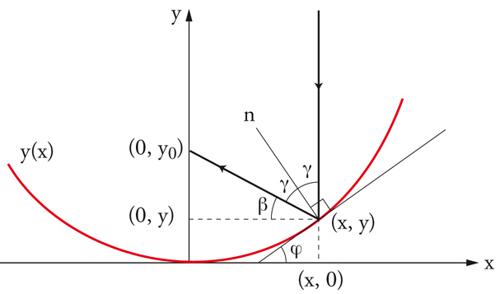
Si consideri (fig. 2) una superficie concava riflettente definita dall'equazione y=y(x), con simmetria azimutale attorno all'asse y e passante per l'origine, e un raggio luminoso parallelo all'asse y, incidente sulla superficie nel punto (x,y). Detto γ l'angolo di incidenza, uguale a quello di riflessione, e φ l'angolo che la tangente nel punto (x,y) alla curva y(x) forma con l'asse delle ascisse, si ha: β=90°−2γ, γ=φ, φ=arctany′ (con y′=dy/dx) e quindi β=90°−2 arctany′. Il raggio riflesso interseca l'asse delle ordinate nel punto y₀=y+xtanβ; dalla trigonometria si ottiene tanβ=cot2φ=[(1/y′)−y′]/2 e quindi y₀=y+x[(1/y′)−y′]/2. Supponiamo ora che la superficie riflettente sia sferica, abbia raggio di curvatura R e sia definita da (y−R)²+x²=R². Dall'equazione per y₀, si ottiene

[1] formula y₀ = R − __√ R² − x² − __ __________ =

√________

2 2 R² − x²

___________

1 1−√ 1− (x²/R²)

= __ R (1− ____________)

___________

2 √ 1− (x²/R²)

che, se il diametro dello specchio è piccolo rispetto al raggio di curvatura R, diventa

[2] formula.

Pertanto, mentre al primo ordine in x/R tutti i raggi passano per un fuoco comune posto in y₀=R/2, gli effetti del secondo ordine fanno sì che i raggi riflessi a distanze differenti dall'asse y convergano in punti differenti.

Se si suppone ora di collocare una lastra fotografica in y₀=R/2, allora i raggi che subiscono una riflessione sulla superficie a distanza x dall'asse, che convergono in un punto più vicino all'origine per un tratto x²/4R, appariranno in fotografia su una circonferenza il cui raggio vale r=(x²/4R)cotβ, cioè

[3] formula

e, all'ordine più basso in x/R, r=(x/R)³×R/2. Per esempio, con uno specchio di 4 m di diametro e raggio di curvatura di 20 m, otteniamo, per i raggi più esterni, x=2 m, x/R=0,1 e r=10 mm. Una lastra fotografica ha tipicamente una risoluzione di 20 μm e quindi, usando uno specchio del genere, si ha una grossa perdita di risoluzione nell'immagine. Se i raggi incidenti non sono paralleli all'asse di simmetria, l'algebra diviene più complicata, ma si può vedere facilmente che, se essi formano con l'asse un angolo ζ piccolo, l'immagine risulta spostata dall'asse di una distanza Rsenζ/2. Nell'esempio precedente, i raggi sulla lastra fotografica sono sparpagliati, come se giungessero ‒ perfettamente focalizzati ‒ con inclinazioni comprese entro un angolo ζ. La risoluzione angolare, se confrontata con il limite di diffrazione di uno specchio di 4 m di diametro, è molto bassa e occorre perciò trovare una forma migliore per lo specchio.

La soluzione ottimale è rappresentata dallo specchio parabolico. Prendendo una superficie rappresentata dall'equazione y=ax², si trova:

[4] formula.

Tutti i raggi paralleli all'asse passano per un fuoco comune e lo specchio parabolico non è affetto da aberrazione sferica. Si supponga di porre nuovamente la lastra fotografica nel fuoco: nell'approssimazione dell'ottica geometrica, l'immagine sarà puntiforme; l'approssimazione deriva dall'avere trascurato che la luce, a causa della sua natura ondulatoria, subisce diffrazione. In ogni caso, per uno specchio di 4 m di diametro, il disco di diffrazione risulta molto piccolo, circa 0,02″ per la luce blu. Mentre per raggi paralleli all'asse lo specchio parabolico dà immagini perfette, altrettanto non si può dire per i raggi fuori asse. Esistono tre aberrazioni importanti: la coma, l'astigmatismo e la curvatura di campo. La coma dà luogo a immagini sfumate, vagamente simili a comete, con il diametro che aumenta linearmente con la distanza dall'asse. L'astigmatismo produce immagini che appaiono come linee ortogonali a diverse distanze focali, con in mezzo un'immagine circolare anziché puntiforme, il cui diametro aumenta in ragione del quadrato della distanza dall'asse. Per di più, queste immagini circolari sono poste su una superficie curva, il che comporta un ulteriore peggioramento dell'immagine se viene usato un rivelatore piano (come quelli a stato solido, per es., un CCD, Charge coupled device).

La grandezza delle aberrazioni dipende dall'apertura relativa (rapporto fra il diametro dello specchio e la sua lunghezza focale). Uno specchio parabolico, con apertura relativa pari a 1/10, a 1° dall'asse ha una coma di 6,8″ e un astigmatismo di 6,3″, mentre nel caso di apertura pari a 1/3 questi valori arrivano rispettivamente a 75″ e 20″. Quindi, se si richiede una qualità di immagine di 0,2″, corrispondente alle migliori condizioni atmosferiche, il raggio accettabile del campo fuori asse è di meno di 10″. Quando si desidera un campo più grande, si rende necessario un correttore, formato da una o più lenti. Per ottenere campi con diametro dell'ordine del grado si ricorre a diversi correttori a tre lenti, la cui utilizzazione introduce effetti cromatici che costringono, in genere, a usare correttori diversi per la luce blu e la luce rossa.

fig. 3 in alto a sinistra

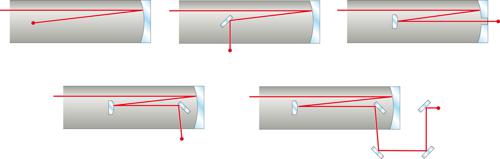
Un altro inconveniente dello specchio parabolico singolo è che gli strumenti per analizzare la luce dell'immagine (apparecchi fotografici, spettrografi, ecc.) devono essere posti sul fascio di luce incidente (fig. 3 in alto a sinistra) ed è difficile evitare che la presenza di questo ingombrante equipaggiamento peggiori ulteriormente la qualità dell'immagine. Una soluzione parziale del problema si è ottenuta con il telescopio newtoniano (fig. 3 in alto al centro), nel quale uno specchio piano posto a una certa distanza dal fuoco deflette lateralmente la luce, permettendo in tal modo di analizzarla fuori dal fascio incidente. Questa soluzione è ormai soltanto di interesse storico, dal momento che la posizione focale lontana dallo specchio principale risulta non equilibrata dal punto di vista meccanico.

Telescopi Cassegrain

Mentre è possibile disporre un apparecchio fotografico o addirittura un CCD (con tutta l'elettronica e il sistema di raffreddamento associati) nel primo fuoco, senza perturbare troppo il fascio incidente, è difficile collocarvi gli spettrografi, più ingombranti. Un sistema Cassegrain a due specchi, la cui prima descrizione risale al 1672, con il fuoco dietro lo specchio primario fornisce una soluzione più soddisfacente (fig. 3 in alto a destra). Nel caso di una montatura altazimutale, questo sistema può essere trasformato in un sistema Nasmyth (fig. 3 in basso a sinistra), nel quale uno specchio piano terziario, posto all'intersezione dell'asse ottico con un asse orizzontale del telescopio, devia lateralmente il raggio luminoso, che esce ed è focalizzato in una posizione nella quale è possibile installare, in ambiente controllato termicamente e senza contribuire alla flessione del tubo del telescopio, un equipaggiamento pesante. La riflessione sul terzo specchio provoca, naturalmente, ulteriore perdita di luce.

L'uso di due specchi rende più complessa la progettazione ottica, perché si deve tener conto delle riflessioni da due superfici, la cui forma può essere scelta secondo diverse combinazioni, ognuna delle quali presenta vantaggi e svantaggi. La maggiore flessibilità di questo sistema consente di ottenere un'immagine fuori asse migliore di quella conseguibile con un paraboloide. Un requisito generale è che lo specchio secondario sia piccolo rispetto al primario, per evitare un eccessivo oscuramento di quest'ultimo. Nell'infrarosso, tale requisito è ancora più importante, dato che bisogna anche ridurre l'emissione dal secondario, che pertanto deve essere posto vicino al fuoco del primario, dove la sezione del raggio riflesso ha un diametro più piccolo. In un telescopio Cassegrain il fuoco del sistema combinato deve stare ben dietro il primario, dove può essere montato l'equipaggiamento pesante; questo risultato si ottiene dando una forma convessa allo specchio secondario e, naturalmente, realizzando un foro centrale nel primario. Nella configurazione Nasmyth, il fuoco deve trovarsi molto esterno rispetto all'asse orizzontale. Dal momento che la maggior parte del peso è costituita dal primario e dalla sua 'cella' di supporto, l'asse orizzontale deve essere vicino al primario; le caratteristiche ottiche di questo sistema non risultano molto diverse da quello Cassegrain.

Si supponga che il primario abbia un diametro D₁ e una lunghezza focale f₁, e che il secondario, di diametro D₂, sia posto a una distanza a davanti al fuoco del primario. Se si considera solamente un fascio incidente parallelo all'asse, allora, affinché il secondario raccolga tutta la luce riflessa dal primario, dev'essere:

[5] formula.

Il fuoco combinato F sia posto a una distanza b dietro la superficie anteriore del primario e sia f la lunghezza focale effettiva del sistema; allora si ha anche:

[6] formula.

Dalle due espressioni si ottiene:

[7] formula.

Quindi, se si vuole che D₂ sia notevolmente più piccolo di D₁, la lunghezza focale effettiva diventa grande. In pratica, lo specchio ha un certo spessore e dietro di esso c'è la cella con l'equipaggiamento per montare gli strumenti; b sarà quindi in generale dell'ordine di D₁/2. In passato, si cercava solitamente di realizzare un sistema con apertura relativa pari a 1/8 e, dato che il primario aveva un'apertura relativa pari a 1/3 (valori più bassi erano difficili da ottenere), si aveva D₁/D₂≈3. In realtà, per includere anche il campo fuori asse il secondario dovrebbe essere un po' più grande. La configurazione utilizzata praticamente da tutti i più grandi telescopi moderni è il sistema Ritchey-Chrétien, nel quale il primario e il secondario sono due iperboloidi accoppiati. Nelle immagini risultanti sono eliminate sia l'aberrazione cromatica sia quella sferica; l'astigmatismo e la curvatura di campo permangono, ma quando sono quantitativamente poco rilevanti si ottiene ancora un campo sufficiente. Se si desidera usare qualche volta anche il primo fuoco, compare l'aberrazione sferica e si rende necessario un correttore del primo fuoco costituito da lenti.

Telescopi Coudé

Nei telescopi a montatura equatoriale non è pratico, dal punto di vista meccanico, collocare pesanti spettrografi ad altissima risoluzione nel fuoco Cassegrain; ciò non soltanto perché il tubo potrebbe deformarsi, e quindi compromettere l'allineamento del secondario, ma anche perché la costruzione dello spettrografo stesso risulterebbe quanto mai complicata, dato che lo strumento dovrebbe operare con diverse orientazioni rispetto al campo gravitazionale e in condizioni di temperatura variabili. A questi inconvenienti ovvia il sistema Coudé a gomito che, utilizzando un certo numero di specchi piani (generalmente uno o tre), porta la luce dall'asse polare del telescopio in una posizione focale fissa. Con la montatura altazimutale, il fuoco Nasmyth soddisfa la maggior parte delle esigenze spettrografiche. Per di più, se si rende necessario portare la luce a uno spettrografo fisso, si possono anche impiegare le fibre ottiche. Comunque, nelle applicazioni interferometriche è sempre meglio portare la luce in una data posizione fissa attraverso un cammino ottico controllato con estrema precisione. A tal fine sono necessarie diverse ulteriori riflessioni a partire dal fuoco Nasmyth (fig. 3 in basso a destra). Le perdite di luce risultanti sono accettabili solamente se si impiegano rivestimenti degli specchi ad alto potere riflettente, che limitano moltissimo il campo delle lunghezze d'onda osservabili.

Aspetti tecnici e ambientali

Materiali per specchi

Gli specchi ‒ cui si richiedono una buona resistenza meccanica, un'alta lucidabilità e, possibilmente, un basso coefficiente di espansione termica ‒ possono essere di metallo, di vetro o di ceramica. Perché un materiale sia lucidabile, deve essere sufficientemente duro e uniforme: metalli come l'alluminio sono troppo teneri. Per tutta la prima metà del XX sec., il materiale preferito è stato quasi sempre il vetro; esso però, pur essendo notevolmente lucidabile, ha un coefficiente di espansione termica relativamente elevato, che quando varia la temperatura dello specchio porta a variazioni della lunghezza focale e anche a deformazioni più gravi. Si sono quindi realizzati numerosi materiali vetrosi o ceramici, come la silice fusa, l'ULE, il Cervit e lo Zerodur, l'ultimo dei quali possiede un coefficiente di espansione termica cento volte inferiore a quello del vetro (10⁻⁷ °C⁻¹). Poichè questi materiali sono costosi, si sono cercate soluzioni più economiche. Una consiste nel costruire uno specchio di cui sia possibile controllare la temperatura, così da poter ritornare all'uso del vetro, sfruttando il fatto che l'isotermicità garantisce la conservazione della corretta forma; del resto, il controllo termico dello specchio è auspicabile comunque, per prevenire i fenomeni di convezione al di sopra di esso. Un'altra soluzione prevede l'uso del metallo; anche in questo caso i problemi dovuti all'espansione termica possono essere evitati con il controllo della temperatura, più semplice che non nel caso del vetro grazie all'elevata conducibilità termica. I primi tentativi di realizzare uno specchio di alluminio con un rivestimento di nichel che ne consentisse la lucidatura fallirono, perché al trascorrere del tempo gli specchi si deformavano. Più recentemente sono stati realizzati, a titolo sperimentale, specchi di acciaio, che sotto questo aspetto si sono rivelati migliori. Nelle applicazioni spaziali sono stati usati in qualche caso, per via del peso ridotto, specchi di berillio, che però risultano di dimensioni piuttosto piccole. Si è pure costruito uno specchio ruotante a mercurio liquido, che non ha bisogno di lucidatura e a cui le forze centrifughe conferiscono la forma richiesta; sfortunatamente, tale specchio può osservare solamente oggetti posti in prossimità dello zenit. La conclusione che si può trarre dal lavoro svolto finora è che i materiali migliori rimangono vetro e ceramica. Dal momento che il costo dei materiali, anche di quelli più dispendiosi come lo Zerodur, incide per meno del 10÷20% sul costo totale di costruzione, è chiaro che la qualità dello specchio rimane il fattore più importante.

Rivestimenti

Le superfici di vetro o di ceramica lucidate hanno bassi poteri riflettenti; devono quindi essere rivestite con uno strato di materiale riflettente, abbastanza sottile da non alterare la forma dello specchio. Di solito si utilizza uno strato di alluminio, il cui potere riflettente è, appena depositato sotto vuoto, dell'ordine dell'85%; l'ossidazione e la corrosione tuttavia riducono tale valore, per cui bisogna depositare un nuovo strato ogni due anni circa. Da qui la necessità di costruire, negli osservatori più remoti, una grande camera a vuoto per il deposito del rivestimento. In un telescopio Cassegrain a due specchi si ha una perdita della luce incidente, la quale è riflessa con un grado di imperfezione che è già del 28%, e arriva al 39% nel fuoco Nasmyth; tali perdite aumentano con l'invecchiamento dell'alluminio. è importante quindi trovare rivestimenti migliori per durata e prestazioni.

Il potere riflettente dei materiali è funzione della lunghezza d'onda della luce incidente. Mentre l'alluminio sembra essere il materiale più indicato per tutta la regione delle lunghezze d'onda superiori a 300 nm (al di sotto della quale l'atmosfera è opaca), altri materiali sono migliori in regioni più limitate dello spettro. Inizialmente si usava l'argento, che ha potere riflettente più elevato, salvo che nell'ultravioletto, ma ha il difetto di essere facilmente danneggiabile dagli agenti atmosferici inquinanti presenti anche soltanto in tracce. L'oro è decisamente migliore sotto questo aspetto ed è stato usato spesso nei telescopi che operano nell'infrarosso. La realizzazione di un materiale di rivestimento più duraturo e con alto potere riflettente su tutto l'arco delle lunghezze d'onda sarebbe un grande passo avanti nell'ottica dei telescopi. Per sistemi ottici destinati a scopi particolari sono stati creati rivestimenti a strati multipli, che hanno, in regioni limitate dello spettro, poteri riflettenti superiori al 99%. Peraltro, il delicato processo che la loro realizzazione richiede ne ha ristretto il campo di applicazione a specchi relativamente piccoli (con diametro minore di 1 m). Questi rivestimenti, mentre risultano assai utili negli strumenti complessi, non sembrano particolarmente vantaggiosi nei grandi telescopi utilizzati a scopi molteplici, eccezion fatta per gli specchi impiegati nell'interferometria, per la combinazione del fascio.

Ottica attiva

fig. 5

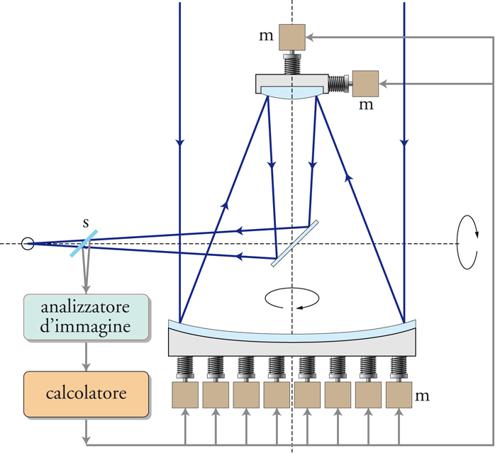
Uno specchio pesante, anche se rigido e spesso, subisce, quando il telescopio si muove, gravi deformazioni dovute alla gravità. È quindi posto in una cella, dove è sostenuto da un appropriato sistema di leve che compensa la variazione degli effetti gravitazionali; se lo specchio è sufficientemente spesso, basta un sistema piuttosto semplice. Nei grandi telescopi il peso di uno specchio di notevole spessore diviene eccessivo e si rendono perciò necessarie soluzioni alternative, tra cui spicca l'ottica attiva. Se uno specchio subisce una deformazione, anche l'immagine di una stella risulta di conseguenza deformata. Con un analizzatore di immagini si può accertare la natura della deformazione e la si può rimuovere, esercitando forze appropriate sullo specchio, ristabilendo la qualità dell'immagine (fig. 5).

L'analizzatore di immagini può essere basato, per esempio, su uno schermo di Hartmann, cioè uno schermo provvisto di una serie regolare di fori, posto sul raggio parallelo o più vicino al piano focale. Quando si colloca una lastra fotografica a una certa distanza dal piano focale, si visualizza un insieme di macchie. Se lo specchio è distorto da deformazioni macroscopiche, anche il reticolo delle macchie risulta deformato; sostituendo la lastra fotografica con un rivelatore a stato solido (CCD), il cui segnale d'uscita è direttamente connesso al calcolatore, si ottengono le posizioni del reticolo in tempo reale.

I supporti dello specchio sono leve e martinetti azionati da motori, che esercitano su di esso forze. Dopo aver calcolato il rapporto tra l'intensità di queste forze e le deformazioni dello specchio, diviene agevole convertire, mediante un elaboratore, i dati così ottenuti in comandi per i motori, in modo che questi applichino le forze necessarie ad annullare la deformazione; per controllare uno specchio di 8 m di diametro sono richieste diverse centinaia di leve. Allo stesso modo si può controllare la posizione dello specchio secondario in un sistema Cassegrain. Dal momento che non sempre si può disporre di una stella di riferimento sufficientemente brillante vicino all'oggetto da osservare, in pratica le misurazioni di ottica attiva sono effettuate saltuariamente; tra una misurazione e l'altra le leve sono manovrate basandosi sull'estrapolazione dei dati ricavati nell'esperienza precedente. L'ottica attiva comporta anche norme meno gravose per la lucidatura degli specchi e, quindi, permette di ridurre i costi e di correggere gli errori. Uno specchio di elevato spessore deve essere lucidato con molta precisione per evitare deformazioni dell'immagine, mentre i difetti di forma di uno specchio sottile soggetto a controllo attivo si possono parzialmente correggere. I difetti su piccola scala, naturalmente, non possono essere corretti: con un sistema di leve si può intervenire soltanto su difetti almeno dell'ordine della distanza tra le leve stesse.

Specchi di grandi dimensioni

Il più grande specchio di elevato spessore mai costruito è quello del telescopio di 6 m di Zelenčuk, in Russia, del peso di 42 t. A parte il costo, il suo principale difetto è la grande inerzia termica, che fa sì che, quando la temperatura ambiente diminuisce, esso resti più caldo dell'aria sovrastante e si inneschino moti convettivi che compromettono la qualità dell'immagine. I più grandi telescopi in costruzione sono realizzati con altri criteri.

Grandi specchi sottili. - In questo caso, lo specchio è sottile (per es., 18 cm per un diametro di 8,2 m negli specchi del VLT dell'ESO), è munito di supporto attivo e ha una superficie liscia e uniforme; il suo difetto principale è la fragilità. È difficile realizzare specchi del genere con diametri superiori agli 8 m, sia perché sono necessari forni, sistemi di lucidatura e camere di deposizione sotto vuoto grandi in proporzione, sia perché il trasporto pone problemi di difficile soluzione.

Specchi più spessi, ma in gran parte cavi. - Lo specchio è composto da uno strato superficiale relativamente sottile, sostenuto da una struttura a nervature per massimizzare la resistenza meccanica mantenendo un peso ridotto. Anche in questo caso è difficile realizzare diametri superiori agli 8 m.

Specchi segmentati. - Singoli elementi di 2÷3 m sono combinati in modo da ottenere un'unica superficie ottica. Gli elementi possono essere relativamente spessi rispetto al loro diametro e sono sostenuti da supporti azionati da motori, controllati da un sistema ottico attivo. Gli elementi devono essere lucidati come paraboloidi fuori asse, con identica lunghezza focale, evitando qualsiasi irregolarità agli spigoli, che avrebbe esiti catastrofici. La questione critica è, naturalmente, la connessione dei vari elementi, dal momento che la presenza di vuoti creerebbe problemi di diffrazione. Il successo del telescopio Keck da 10 m, situato alle Hawaii, mostra che le varie difficoltà possono essere superate. Il vantaggio principale consiste nelle dimensioni ridotte dei singoli elementi, che non necessitano di grandi impianti per la realizzazione o l'alluminatura.

Telescopi a specchi multipli. - Vari specchi circolari sono posti su un'unica montatura e la loro luce è combinata mediante un'ottica adeguata.

Telescopi a schiera. - È stato abbandonato il principio della montatura in comune e i telescopi operano singolarmente. La luce può essere combinata mediante specchi, oppure le immagini ottenute dai rivelatori dei singoli telescopi possono essere composte elettronicamente.

Il vantaggio dei telescopi a specchi multipli e di quelli a schiera consiste nel fatto che la lunghezza focale degli specchi primari è inferiore a quella di un unico specchio monolitico che abbia la stessa superficie e il medesimo rapporto focale (dove per rapporto focale si intende il rapporto tra la lunghezza focale e il diametro), con la conseguenza che il telescopio è più corto e subisce una flessione meno accentuata, e risulta otticamente più semplice adattarvi alcuni spettrografi. Lo svantaggio più rilevante consiste nella necessità di aumentare il numero degli specchi, e ciò può portare a notevoli perdite di luce, a meno di non utilizzare rivestimenti ad alto potere riflettente, che comunque riducono il campo delle lunghezze d'onda osservabili. In alternativa si possono connettere i telescopi mediante fibre ottiche, una soluzione praticabile quando si osservano uno o pochi oggetti stellari, ma meno adatta al trasferimento di immagini. In un sistema di telescopi a schiera, alcuni elementi (motori, montature, cuscinetti) devono essere costruiti separatamente per ciascun telescopio, mentre un telescopio multispeculare prevede una sola unità, benché più grande. Il vantaggio di un sistema a schiera sta nel fatto che esso fornisce informazioni interferometriche più esaurienti.

Meccanica dei telescopi e cupole

Le flessioni meccaniche ‒ che in passato creavano gravi problemi nelle montature equatoriali ‒ sono state molto ridotte con l'introduzione della montatura altazimutale e dei moderni metodi di progettazione (calcolo degli elementi finiti, ecc.), mentre le flessioni residue possono essere compensate con metodi di ottica attiva. Nonostante questi progressi, risulta ancora consigliabile che la struttura del telescopio sia la più compatta possibile, per ridurre la necessità di costruire grandi cupole dai costi elevati e dalla grande inerzia termica. La lunghezza del tubo di un telescopio Cassegrain è determinata dalla lunghezza focale dello specchio primario, perciò conviene rendere il rapporto focale il più piccolo possibile. In passato si sono adottati valori intorno a 3; oggi si tende a realizzare valori inferiori. I rapporti focali molto bassi presentano due inconvenienti: la lucidatura dello specchio è più difficile e la regolazione del relativo sistema ottico più delicata. Un tubo lungo comporta una grande cupola; il notevole volume di aria presente in essi è difficile da controllare termicamente e le correnti di convezione compromettono la qualità dell'immagine. È quindi consigliabile un tubo corto. Con la montatura altazimutale è possibile circondare il telescopio con una struttura che ruota in modo a esso solidale e che contiene un volume di aria molto minore rispetto a una cupola sferica.

Siti

I telescopi possono ben funzionare soltanto se collocati in luoghi adatti, che minimizzino la degradazione della qualità dell'immagine per cause ambientali. Per i telescopi ottici, il requisito più ovvio è la scarsa nuvolosità. I telescopi, originariamente, erano costruiti in zone dove si hanno notti serene solamente nel 50% dei casi o meno. In seguito furono scelti posti più adatti, con notti serene nel 70% ed, eccezionalmente, nell'85% dei casi (come nell'estremo nord del Cile). Il secondo requisito è un'atmosfera stabile, in cui siano ridotte al minimo le turbolenze, che sono due tipi: quelle dell'alta atmosfera, associate alla circolazione atmosferica globale, e gli effetti locali, connessi con le caratteristiche topogeografiche. I venti forti sono sfavorevoli e devono essere evitati anche per i loro effetti meccanici. È molto probabile che si abbia una forte turbolenza nell'alta atmosfera ai tropici, dove prevale una notevole convezione ascensionale, e alle latitudini in cui è presente la corrente veloce di alta quota. Nel mezzo vi è una regione più favorevole, in cui si riscontra un lento movimento discendente nell'atmosfera e dove le perturbazioni sono più rare; allo stesso tempo, questa regione ha un ridotto contenuto di vapore, a causa del tiraggio verso il basso, e questo fattore è particolarmente importante a lunghezze d'onda infrarosse e submillimetriche. Le aree continentali con bassa nuvolosità si riscaldano durante il giorno e si raffreddano di notte, dando luogo a moti convettivi, mentre l'aria è più stabile sopra gli oceani. Le collocazioni migliori risultano essere quindi sulle isole o in prossimità delle coste. Le basse temperature oceaniche riducono l'evaporazione e la convezione, e le correnti fredde lungo le coste occidentali dei continenti creano condizioni particolarmente favorevoli.

L'altitudine riveste un ruolo di grande importanza. A 3000 m l'atmosfera soprastante è ridotta quasi del 25% e la trasparenza atmosferica, soprattutto ai raggi ultravioletti e infrarossi, è sensibilmente migliore. Il criterio generale è quindi chiaro: i telescopi dovrebbero essere collocati in alta montagna, vicino a un oceano freddo, a latitudini relativamente basse. I migliori siti conosciuti sono la sommità del Mauna Kea (4200 m) nelle Hawaii, il nord del Cile (con montagne di 2000÷3000 m molto vicine alla costa) e i luoghi più alti delle isole Canarie, dove però l'umidità non è altrettanto bassa. Anche la California e la Namibia sono posti relativamente favorevoli. L'Australia occidentale beneficia di una corrente oceanica fredda, ma non ha montagne alte. Un altro luogo probabilmente molto adatto è l'Antartide. La costa antartica è un'area battuta da forti bufere, ma al centro del continente l'aria è molto calma, limpida e secca, e vi sono rilievi alti fino a 4500 m.

Ottica adattativa

Anche al di sopra dei siti migliori si verificano turbolenze atmosferiche che producono fluttuazioni nell'immagine, con frequenze di 1÷100 Hz. Per correggere questi effetti, si potrebbe pensare di applicare i principî dell'ottica attiva, ma la grande massa dello specchio primario rende difficili correzioni su scale temporali inferiori a 1÷10 secondi. Si potrebbe ovviare a questo inconveniente inserendo sul cammino della luce uno specchio piano più piccolo, sottile e flessibile: la sua deformazione consentirebbe infatti di eliminare gli effetti atmosferici dall'immagine della stella, ottenuta utilizzando un analizzatore di immagini secondo uno schema analogo a quello mostrato nella fig. 5. In questo caso il problema principale consiste nella scarsa correlazione tra gli effetti atmosferici nelle diverse direzioni. Il campo isoplanatico (ossia esente da aberrazione di coma) sul quale la correlazione è buona risulta essere di soli 10÷20 secondi d'arco di diametro a lunghezze d'onda ottiche, mentre la situazione migliora nell'infrarosso, in conseguenza del fatto che tale diametro varia proporzionalmente a λ^6/5.

Se si vuole raffinare l'immagine di un oggetto, è necessario trovare, all'interno del campo isoplanatico, una stella di riferimento sufficientemente luminosa, per determinare le opportune correzioni; nella maggioranza dei casi, tuttavia, una tale stella non risulta disponibile. In alternativa si potrebbe creare nell'alta atmosfera, con l'aiuto di un laser, una stella artificiale da utilizzare come sorgente di riferimento. Un potente fascio laser di luce gialla subisce una diffusione risonante da parte degli atomi di sodio, presenti nella mesosfera a circa 100 km d'altitudine: se il fascio è sufficientemente collimato, si riesce a creare una sorgente di luce di tipo stellare. Dal momento che gli strati più alti dell'atmosfera, che causano la degradazione dell'immagine, si trovano a circa 10 km di quota, il cammino fino alla 'stella laser' attraversa tutti i relativi strati. Nel caso di stelle piuttosto luminose, si potrebbe anche usare il nucleo dell'immagine stellare come sorgente di riferimento.

Prestazioni dei telescopi terrestri e spaziali

Si supponga di avere un telescopio con diametro d, potere riflettente ideale e dotato di un rivelatore privo di rumore e dal rendimento perfetto, che sia posto dietro un filtro perfettamente trasmittente con una larghezza di banda di 1 Å, e di osservare per un tempo t una stella che fornisce un flusso di luce di n fotoni/(cm² s Å). Il numero dei fotoni ricevuti sarà πd²nt/4 e il rumore (l'incertezza dovuta alle fluttuazioni statistiche) sarà (πd²nt/4)^1/2. Stabiliamo che il rapporto segnale/rumore, S/N, debba avere il valore (S/N)₀: sarà allora S/N=(πd²nt/4)^1/2=(S/N)₀ e, pertanto, il tempo necessario all'osservazione è t=(4/πnd²)(S/N)²₀. Si supponga ora che la stella sia osservata insieme a uno sfondo di b fotoni/(cm² s Å): si osservano prima la stella e lo sfondo insieme, quindi, escludendo la stella, si misura il contributo dello sfondo e poi si sottraggono le due misure per ricavare il flusso proveniente dalla sola stella. Si consideri il caso n≪b; il rumore sarà circa (πd²bt/4)^1/2 in ciascuna delle misure e il rumore sulla differenza varrà √2×(πd²bt/4)^1/2. Si ha così:

[8] formula.

e il tempo necessario all'osservazione diviene:

[9] formula.

Il tempo di osservazione varia con l'inverso del quadrato del flusso di luce proveniente dalla stella e ridurre lo sfondo di un certo fattore ha il medesimo effetto che aumentare dello stesso fattore l'area del telescopio. Per i telescopi terrestri lo sfondo è dovuto alla somma della luce zodiacale, di quella delle stelle deboli non risolte, della luce diffusa dalla polvere interstellare e di quella generata nell'atmosfera terrestre. La quantità della luce di sfondo dipende dall'ampiezza dell'angolo solido sotto cui si osserva la luce della stella. Sulla Terra, per i grandi telescopi l'angolo solido è determinato dalla turbolenza atmosferica e, nelle posizioni migliori, ha un'ampiezza fissa, tipicamente dell'ordine di un secondo d'arco al quadrato. Nello spazio, se l'ottica è a diffrazione limitata, tale angolo diviene molto più piccolo, cioè dell'ordine di (λ/d)² radianti. In questo caso si trova:

[10] formula.

Per il telescopio spaziale Hubble, da 2,4 m a 5000 Å, il fattore λ/d vale 0,04 secondi d'arco e quindi b è minore per oltre un fattore cento rispetto al caso di un grande telescopio terrestre; per tale ragione Hubble risulta più adatto all'osservazione di stelle molto deboli.

Un altro modo di considerare questi risultati è chiedersi quale sia la sorgente di luce più debole che può essere osservata in un determinato tempo e con un dato (S/N)₀. Quando lo sfondo è trascurabile, si ha:

[11] formula.

mentre quando prevale lo sfondo si ha:

[12] formula.

In quest'ultimo caso, aumentando l'area di raccolta del telescopio o il tempo di osservazione, si ottiene un miglioramento del flusso limite soltanto in ragione della radice quadrata di queste quantità. Si è supposto di avere un potere riflettente perfetto, una larghezza di banda di 1 Å e un contatore di fotoni perfetto. Se invece il potere riflettente risulta r, la larghezza di banda w e l'efficienza di conteggio dei fotoni η, si dovrà moltiplicare d² e b ovunque per rwη. Quando prevale lo sfondo, anche un piccolo telescopio spaziale a diffrazione limitata fornisce prestazioni migliori rispetto a un telescopio terrestre da 10 m. Comunque, quando dev'essere raggiunta una grande risoluzione spettroscopica (corrispondente a piccolissimi valori di w), il flusso minimo osservabile in un tempo ragionevole è tale che lo sfondo è trascurabile anche sulla Terra e un grande telescopio terrestre risulta migliore. Lo stesso accade per grandi oggetti uniformi quando l'angolo solido sia lo stesso per i telescopi spaziali e per quelli terrestri.

Bibliografia

Bahcall, Spitzer 1982: Bahcall, John N. - Spitzer, Lyman jr, The space telescope, "Scientific American", 247, 1982, 1, pp. 40-51.

Beckers 1993: Beckers, Jacques M., Adaptive optics for astronomy, "Annual review of astronomy and astrophysics", 31, 1993, pp. 13-62.

Kuiper, Middlehurst 1960: Kuiper, Gerard P. - Middlehurst, Barbara M., Telescopes, Chicago, University of Chicago Press, 1960.

Léna 1996: Léna, Pierre, Astrophysique: méthodes physiques de l'observation, 2. ed., Paris, InterEditions-CNRS, 1996.

Ulrich 1988: ESO conference on very large telescopes and their instrumentation, edited by Marie-Helene Ulrich, München, Garching, 1988, 2 v.

Wilson 1996: Wilson, Raymond N., Reflecting telescope optics, Berlin, Springer, 1996.