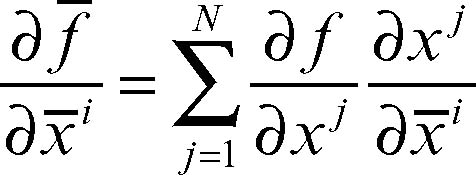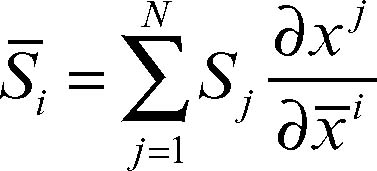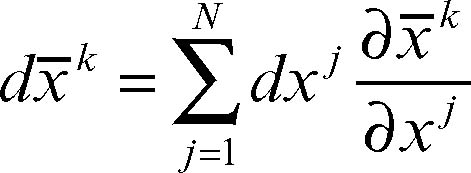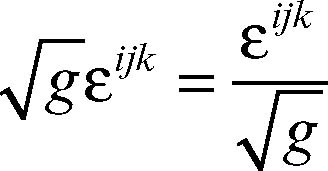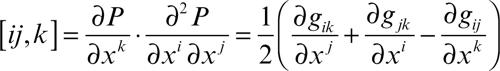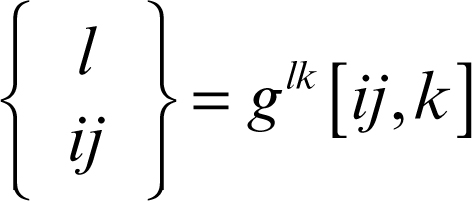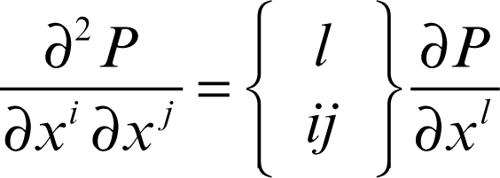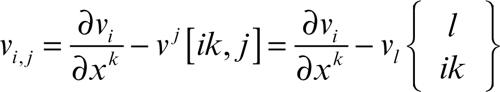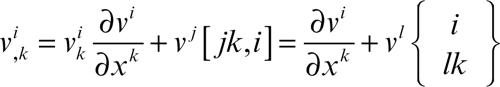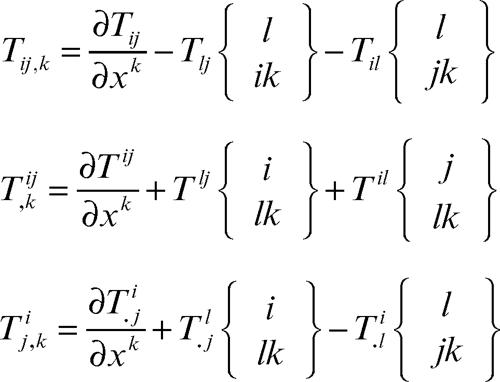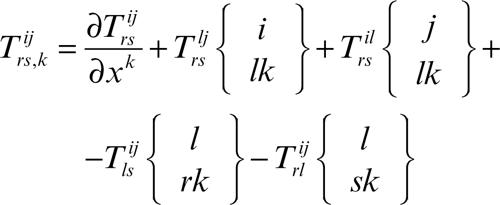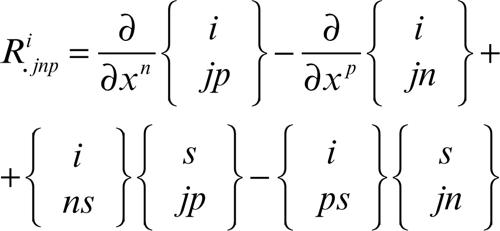tensore
tensore
tensore ente matematico formulato nell’ambito della → geometria differenziale e oggi studiato come un capitolo dell’→ algebra lineare. Il nome tensore nasce dalla teoria dell’elasticità, in quanto lo stato di tensione di un corpo elastico è descritto appunto da un tensore, detto tensore degli sforzi. La nozione di tensore generalizza quella di → vettore in più sensi. Da un lato, perché un tensore può avere un numero arbitrario di indici, dall’altro perché il suo formalismo è indicato per trattare cambiamenti qualsiasi di coordinate ed è quindi adatto allo studio di campi non solo in spazi euclidei ma in generiche varietà differenziabili. Le convenzioni del calcolo tensoriale si rivelano assai efficaci per esprimere le equazioni della fisica matematica in forma molto compatta e versatile. Esse si basano su due fondamenti notazionali: la distinzione tra sistemi covarianti, controvarianti (e invarianti), e la convenzione di saturazione degli indici.
Si consideri lo spazio RN descritto dalle coordinate (x 1, x 2 …, xN), e sia (x̄ 1, x̄ 2, …, x̄N) un secondo sistema di coordinate. Per esempio, si può pensare a una rotazione degli assi, ma anche al passaggio da coordinate cartesiane a sferiche o cilindriche. Le nuove coordinate x̄ i saranno dunque funzioni delle vecchie:
Per convenzione, se un indice i è libero, si intende che assume tutti i valori compresi tra 1 e N, e si omette la scrittura 1 ≤ i ≤ N che appare pleonastica. Pertanto la scrittura precedente è da intendersi non come una equazione ma come un sistema di N equazioni in N variabili: le coordinate del nuovo sistema in funzione di quelle del vecchio. Si supponga che il cambiamento di variabili sia biunivoco e di classe C 1, il che è garantito se lo jacobiano
è diverso da zero. Nel nuovo sistema una funzione ƒ(x 1, x 2, …, xN) si trasformerà in ƒ̄ (x̄ 1, x̄ 2, …, x̄N). I valori della funzione, naturalmente, non mutano, ma mutano quelli delle sue derivate parziali, risultando, per la regola di derivazione delle funzioni composte
Questo tipo di dipendenza è detto covariante. In generale, un sistema (di scalari o di vettori) a un indice Sj è detto covariante se le sue componenti mutano secondo la legge
Covariante, per esempio, è anche il sistema di vettori bj dato dalle derivate
che individua le direzioni delle linee coordinate e costituisce una base locale per RN. In particolare, se le x j sono coordinate cartesiane ortogonali (monometriche), questi vettori non sono altro che i versori ij, degli assi, espressi in forma covariante. Viceversa, i differenziali delle variabili dxk mutano con la legge
e si parla allora di sistema controvariante. Per convenzione gli indici in basso (pedici) indicano un sistema covariante, quelli in alto (apici) un sistema controvariante, eccettuate le coordinate x j o x̄k in cui l’indice è sempre in alto pur non formando un sistema controvariante. Quando invece un cambiamento di variabili non muta il valore delle componenti, il sistema si dice invariante e l’indice si mette sotto la lettera che lo rappresenta:
Per comprendere la distinzione tra i due tipi di sistemi, covariante e controvariante, si ricordi che un vettore v (invariante) si può descrivere in due modi in un sistema di riferimento. In un primo modo, si esprime v come combinazione lineare degli N vettori
scrivendo
I coefficienti v j si dicono componenti controvarianti di v. Si può però assegnare v calcolando i prodotti scalari di v per i vettori bj e ottenendone le componenti covarianti
Se in un cambiamento di variabili i vettori bj crescono, mantenendo la stessa direzione, anche i prodotti scalari vj crescono, mentre i coefficienti v j diminuiscono. Questo giustifica il nome di componenti covarianti e controvarianti dato ai due tipi di rappresentazione.
Solo nel caso di basi formate da versori ortogonali le due espressioni coincidono; in caso contrario si possono trasformare l’una nell’altra mediante il cosiddetto tensore fondamentale gij (si veda oltre).
Un’ulteriore convenzione (attribuita a Einstein) è quella di non scrivere il simbolo di sommatoria: ogniqualvolta un indice compare due volte, si intende che viene eseguita la somma, con quell’indice che varia da 1 a N. Si dice che quell’indice è saturato; esso è una variabile muta e può essere sostituito con qualsiasi altra lettera, purché diversa da quelle (libere) che già compaiono nell’espressione. Perciò le ultime due precedenti sommatorie si scrivono semplicemente come
o
(ma anche come
cambiando il nome dell’indice libero, che è comunque quantificato universalmente: ∀r, 1 ≤ r ≤ N) e
Quanto detto per sistemi a un indice si estende a sistemi a due o più indici. Perciò un sistema Tik è covariante se soddisfa le regole di trasformazione
controvariante se soddisfa
e di tipo misto se vale la regola di trasformazione
In questo caso il puntino indica che a pedice le lettere k e h occupano la seconda posizione: dunque il sistema è controvariante nel primo indice e covariante nel secondo, distinguendosi così da un sistema misto Th.j.
Un particolare tensore misto è il tensore delta di Kronecker, δki, le cui componenti valgono 1 per i = k, 0 per i ≠ k (→ Kronecker, simbolo di).
In definitiva, un tensore di ordine n è un ente a n indici, che dipende dal sistema di coordinate e si trasforma, al variare di tale sistema, secondo le regole indicate per le componenti covarianti o controvarianti. Un tensore di ordine n avrà dunque 2n forme, a seconda che ciascun indice si comporti in modo covariante o controvariante.
Algebra dei tensori
Nell’insieme dei tensori è possibile definire le seguenti operazioni:
• addizione: si esegue, elemento per elemento, tra tensori della stessa natura (numero di componenti, e tutte dello stesso tipo). Perciò si può definire Aij + Bij, ma non Aij + Bij;
• trasposizione di un tensore: si ottiene scambiando due indici dello stesso tipo. Per esempio, un trasposto di Tikj è Tijk, ma anche Tkij, mentre in Tjik si possono trasporre gli indici i e k ma non j. Un tensore uguale al suo trasposto si dice simmetrico rispetto a quella coppia di indici; un tensore covariante (o controvariante) è detto simmetrico senza ulteriori indicazioni se lo è rispetto a qualsiasi coppia di indici. Analogamente, un tensore che muta segno scambiando due indici (dello stesso tipo) si dice emisimmetrico rispetto a quegli indici, ed è emisimmetrico se è covariante o controvariante e il cambiamento di segno avviene per tutte le coppie di indici. Se ne deduce che un tensore emisimmetrico di ordine dispari è necessariamente nullo;
• prodotto esterno: dati due tensori, per esempio Aij e Bkrs, è possibile moltiplicarli elemento per elemento, ottenendo il tensore Ckijrs = AijBkrs;
• prodotto interno: si ottiene da due tensori saturando un indice covariante con uno controvariante: AijB jk = Cik;
• è infine possibile saturare un indice con un altro nello stesso tensore, purché misto, ottenendo un tensore di ordine n − 2 detto tensore contratto del tensore dato. Per esempio, l’espressione vj = Aiij fornisce un vettore covariante contraendo un tensore di ordine 3.
L’algebra dei tensori permette di sviluppare un calcolo all’interno del loro insieme (→ calcolo tensoriale).
Tra i tensori assume particolare importanza il cosiddetto tensore metrico o fondamentale gij, definito dalla relazione che lega l’elemento di lunghezza ds di una linea agli incrementi dxi delle coordinate. Precisamente, si pone ds2 = gijdxidxj. Se lo spazio è euclideo e riferito a un sistema cartesiano (monometrico) risulta gij = δij, ma in generale ciò non è vero. Infatti, preso uno spostamento
il quadrato del suo modulo è dato da
da cui si deduce che le componenti covarianti del tensore fondamentale sono i prodotti scalari dei vettori derivati:
che sono le componenti covarianti dei vettori covarianti
e formano dunque un tensore doppio covariante. La natura tensoriale di gij si può anche dedurre dal fatto che i differenziali dxi sono controvarianti e ds2 è un invariante.
Il tensore fondamentale è simmetrico e se si suppone che la forma quadratica associata sia definita positiva, l’espressione di ds2 è positiva e rappresenta effettivamente una distanza in RN (o su una varietà N-dimensionale, che viene detta, in questo caso, varietà riemanniana). Nel caso della relatività, la forma è invece indefinita e si ha una cosiddetta varietà pseudoriemanniana.
Le componenti con i ≠ j si annullano se e solo se i corrispondenti vettori sono ortogonali. Il tensore fondamentale permette il passaggio dalle componenti controvarianti a quelle covarianti di un vettore v mediante le formule vi = gijv. Il passaggio inverso viene fatto attraverso il tensore fondamentale controvariante gij, che è semplicemente l’inverso (matriciale) di gij, formato dunque dai complementi algebrici di gij divisi per il determinante g = det(gij). Lo stesso vale per tensori di ogni ordine: per esempio Trk = grjTkj = grjgkpTjp. Si noti che le versioni covariante δik e controvariante δik del tensore delta di Kronecker non assumono solo i valori 0 e 1, ma per esempio δik = gij δ jk = gik.
Gli usuali prodotti, scalare, vettoriale e misto, di vettori in R3 possono essere espressi in notazione tensoriale.
Il prodotto scalare di due vettori u e v si esprime componendone le componenti covarianti e controvarianti:
Il prodotto vettoriale in R3 si esprime mediante la composizione dei due vettori con il cosiddetto tensore di Levi-Civita, o di permutazione, εijk definito da
Si ha infatti che u × v è descritto (in modo covariante) da εijku jvk. Il doppio prodotto misto u × v ⋅ w = w ⋅ u × v si ottiene a questo punto semplicemente come εijku jvkw i. Il prodotto
non è un tensore, ma le sue componenti valgono 0 se due indici sono uguali, 1 se gli indici hanno permutazione pari (123, 231, 312), −1 se hanno permutazione dispari (132, 321, 213).
Derivazione covariante
Anche se le derivate
formano un sistema covariante di vettori e quindi si rappresentano come un tensore (il tensore fondamentale), le loro derivate
non formano un tensore triplo, perché non si trasformano con le leggi che caratterizzano la natura tensoriale di un sistema doppio di vettori. Ne consegue che derivando, per esempio, le componenti covarianti
di un vettore v, si ha
e il secondo addendo non è un tensore.
Per ottenere una derivata che abbia carattere tensoriale, si introducono i simboli di Christoffel (simmetrici rispetto ai due indici accoppiati, qui i e j):
• di prima specie
• di seconda specie
da cui
Anche questi simboli non sono tensori, ma si mostra che l’espressione
è un tensore, detto derivato covariante di νi. Analogamente, se si deriva un vettore v dato in forma controvariante, si ottengono le formule
Le notazioni non sono sempre univoche; talvolta sono usate la barra / al posto della virgola, per separare gli indici che indicano le componenti da quelli di derivazione, e le parentesi graffe al posto delle quadre nei simboli di prima specie. Si noti che i simboli di Christoffel si annullano in coordinate cartesiane ortogonali, ma non in coordinate ortogonali qualsiasi, come per esempio le coordinate sferiche.
Per la derivata covariante di un tensore doppio si ottengono le seguenti tre formule:
Generalizzando si avrà, per esempio:
Le derivate covarianti del tensore fondamentale sono nulle. Valgono ancora, per le derivate covarianti, le regole per la derivazione di una somma e di un prodotto, esterno o interno. Per esempio:
La divergenza Ai di un vettore controvariante si ottiene contraendo con la derivata covariante o in qualsiasi forma equivalente: A,ii = Aj,ig ij = A.j,igij.
Per un tensore di ordine n, ci sono a priori n divergenze distinte: per esempio per n = 2, si hanno le formule D′ k = T,iki e D″ k = T,iik; esse coincidono per tensori simmetrici.
Per quanto riguarda il rotore, si può dare una definizione per N qualsiasi; nel caso N = 3 il rotore ha la forma controvariante Ri = εijkAk,j, in cui ε è il tensore di Levi-Civita.
Con le derivate seconde, sorge un nuovo problema: in generale, infatti, le derivate seconde covarianti di un tensore, pur essendo tensori, non commutano. Entrano infatti in gioco non solo i simboli di Christoffel, ma anche le loro derivate. Si trova allora, nel caso di un vettore, la formula di commutazione
nella quale compare il cosiddetto tensore di Riemann (o di Riemann-Christoffel), definito da
Dato che i simboli di Christoffel si esprimono tramite le derivate del tensore fondamentale, il tensore di Riemann-Christoffel dipende solo da questo e dalle sue derivate fino al secondo ordine. Esso è emisimmetrico rispetto agli ultimi due indici. Lo stesso naturalmente avviene per la forma covariante di tale tensore, Rijnp = gikRkjnp, che risulta emisimmetrico anche rispetto alla prima coppia di indici. Valgono inoltre la simmetria Rijnp = Rnpij e la relazione Rijnp + Rinpj + Ripjn = 0. Se ne deduce che il numero delle componenti distinte del tensore di Riemann-Christoffel è N 2(N 2 − 1)/12.
Contraendo il tensore di Riemann si ottiene il tensore di Ricci (pure indicato con la lettera R, ma ben distinguibile perché di ordine 2 anziché 4), definito da Rjn = Rkjnk. Esso risulta simmetrico. Questi tensori sono utilizzati per definire le proprietà geometriche intrinseche di una → varietà, in particolare le sue curvature, le linee geodetiche e la nozione in essa di parallelismo.