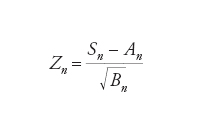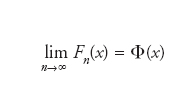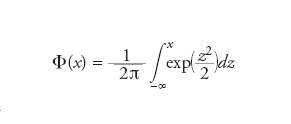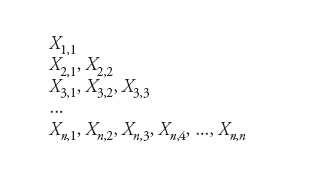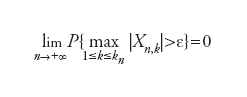teorema del limite centrale

teorema del limite centrale

Nome collettivo per una serie di teoremi limite in teoria della probabilità che stabiliscono condizioni sotto le quali somme o altre funzioni di un grande numero di variabili casuali indipendenti hanno distribuzione di probabilità vicina alla distribuzione normale o gaussiana. La versione classica del teorema del limite centrale tratta il caso della somma S_n=X₁+...+X_n di una successione X₁,...,X_n,... di variabili casuali indipendenti, ciascuna con valore atteso EX_k=a_k e varianze DX_k=[E(X_k-EX_k)²]^1/2=b_k finite. Definiamo ora A_n=ES_n=a₁+...+a_n e B_n=DS_n=b₁+...+b_n (questa seconda uguaglianza è valida in quanto le variabili X_k sono assunte indipendenti) e consideriamo le variabili

Esse sono dette somme normalizzate, in quanto hanno valore atteso nullo e varianza pari a 1. Indicando con F_n(x)=P{Z_n〈x} le rispettive distribuzioni di probabilità, il teorema del limite centrale afferma che, per ogni x∈ℝ,

dove

è appunto la funzione di distribuzione normale standard corrispondente alla densità normale con valore atteso nullo e varianza unitaria. Le condizioni precedenti possono essere sensibilmente indebolite, ma il loro significato è sempre di imporre che le variabili casuali considerate (o loro opportune funzioni) siano trascurabili rispetto alla loro somma. Tale circostanza è chiarita considerando uno schema triangolare di variabili casuali

con X_n,k=(X_k−a_k)/√B_n e 1≤k≤n. Le variabili casuali in ciascuna riga sono allora indipendenti e Z_n=X_n,1+...+X_n,n. Le usuali condizioni per la valità del teorema del limite centrale implicano che X_n,k è asintoticamente trascurabile al crescere di n. Viceversa, dato uno schema triangolare e supponendo che le somme Z_n abbiano una densità limite di probabilità per n che tende a infinito (ma esistono condizioni necessarie e sufficienti perché questo avvenga) è possibile dimostrare che essa è normale se e solo se per ogni ε>0

ovvero se il termine massimo in Z_n diventa trascurabile rispetto alla somma stessa.

→ Leggi di scala