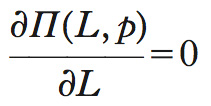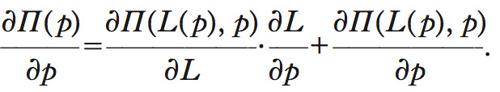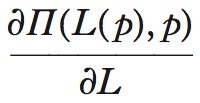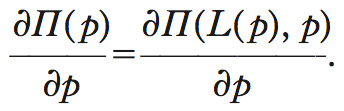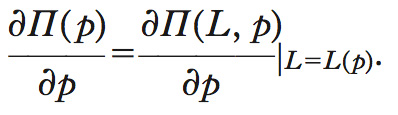inviluppo, teorema dell’
inviluppo, teorema dell¿
inviluppo, teorema dell’ Teorema concernente il problema, che nella teoria economica si pone con frequenza, di determinare l’impatto su una scelta massimizzante derivante dalla variazione di un parametro, da cui tale scelta dipende. Sia, per es., Π(L, p) il profitto di un’impresa espresso in funzione della quantità impiegata del fattore produttivo lavoro L e del prezzo p del prodotto. Il profitto dipende dal prezzo dell’output sia direttamente sia indirettamente attraverso la scelta ottimale della quantità di lavoro: ragionevolmente, quanto maggiore è il prezzo, tanto maggiore la quantità di lavoro che l’azienda sarà indotta a utilizzare. Sia allora L(p) la quantità di lavoro che massimizza il profitto dato il prezzo p, ossia la soluzione della condizione del primo ordine per un massimo:
e Π(p)=Π(L(p), p) il corrispondente valore del profitto. La funzione Π(p) prende il nome di funzione valore. Il teorema dell’i.
Poiché L(p) è la quantità di lavoro che massimizza il profitto, la derivata formula
è, per quanto detto, uguale a 0; si ottiene quindi formula
Questo risultato, noto appunto come teorema dell’i., mostra che l’effetto sulla funzione valore di una variazione del prezzo, più in generale di un parametro, si riduce al solo effetto diretto, essendo nullo l’effetto indiretto sulla scelta massimizzante del fattore lavoro. Ciò consente di affermare che la derivata parziale della funzione valore rispetto al parametro p è uguale alla derivata parziale della stessa quando tale derivata è valutata in corrispondenza della scelta ottimale: formula