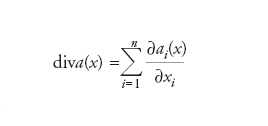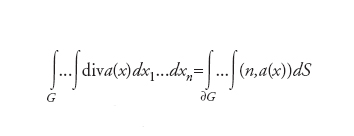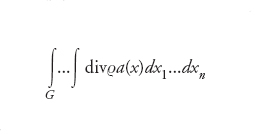teorema della divergenza

teorema della divergenza

Una formula nel calcolo di integrali multipli di funzioni di più variabili che stabilisce un legame tra un integrale (di volume) su un dominio n-dimensionale e un integrale (di superficie) sul suo bordo (n-1)-dimensionale. Sia a(x) un campo vettoriale di componenti a_i(x) (i=1,...,n) in un punto x=(x₁,...,x_n) di ℝⁿ tale che le a_i(x) stesse e le derivate parziali ∂a_i(x)/∂x_i siano integrabili secondo Lebesgue su un dominio G (per es., continue se G è chiuso e limitato) il cui bordo ∂G sia l’unione di un numero finito di superfici regolari (n−1)-dimensionali orientate utilizzando il versore (vettore di lunghezza unitaria) normale n. Ricordiamo che il campo scalare definito dalla

è detto divergenza di a(x). Notiamo che, indicando con il simbolo ∇=(∂/∂x₁,...,∂/∂x_n) l’operatore gradiente e con ( , ) l’usuale prodotto scalare in ℝⁿ, si può scrivere diva(x)=(∇,a(x)). Il teorema della divergenza prende allora la forma

dove l’integrale a secondo membro è esteso al bordo ∂G e dS indica l’elemento infinitesimo di (iper)superficie. Esso è detto flusso del campo attraverso la (iper)superficie ∂G. Se il campo vettoriale è il campo di velocità del flusso stazionario (cioè indipendente dal tempo) di un fluido incompressibile con densità ϱ, allora diva(x) coincide con l’intensità di una sorgente se diva(x)>0 (o di un pozzo se diva(x)〈0) nel punto x e l’integrale

con la quantità totale di fluido che esce dalla sorgente (o precipita nel pozzo) nell’unità di tempo. Il teorema della divergenza afferma allora che, poiché il fluido è incompressibile, una pari quantità di esso dovrà uscire (entrare) attraverso il bordo della regione G.

→ Equazioni differenziali: problemi non lineari