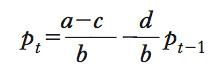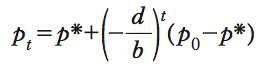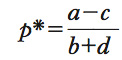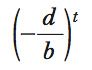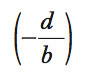ragnatela, teorema della
ragnatela, teorema della
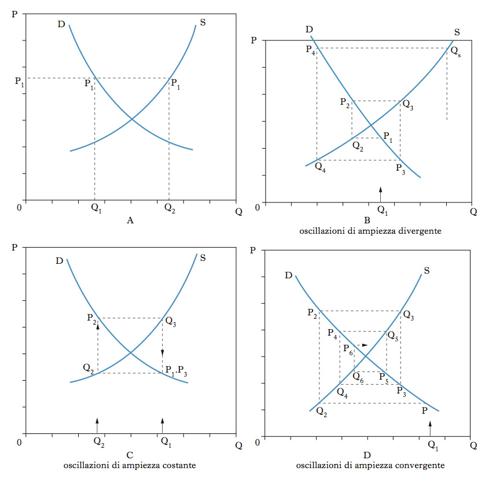
Modello sviluppato dall’economista N. Kaldor (➔) per spiegare le oscillazioni del prezzo di mercato nel tempo. Il teorema della r. identifica sotto quali condizioni il prezzo converge all’equilibrio di mercato in presenza di aspettative statiche. Il mercato è descritto da una funzione della domanda qDt=a−bpt; da una funzione di offerta qSt=c+dptA; dalla condizione di equilibrio qDt=qSt, dove qDt e qSt sono le quantità domande e offerte nel periodo t; pt e ptA il prezzo corrente nel periodo t e quello atteso dai produttori nel medesimo periodo; a, b, c e d sono parametri tutti positivi. Il modello, che è chiaramente incompleto, poiché manca una spiegazione della formazione del prezzo atteso, assume aspettative statiche: ptA=pt−1, e cioè il prezzo atteso nel periodo t coincide con il prezzo di equilibrio del periodo precedente. Con questa ipotesi, la quantità offerta in ogni periodo è rigidamente fissata. Ne consegue che, se nel periodo precedente il prezzo è stato alto, in quello corrente la quantità offerta è elevata e viene assorbita dalla domanda solo a un prezzo basso. Più in particolare (figura A), se il prezzo atteso è p1, la quantità prodotta è q2, che può essere assorbita dalla domanda solo a un prezzo più basso; ma, allora, nel periodo ancora successivo la quantità prodotta sarà bassa e il prezzo alto, con un’oscillazione continua dello stesso. In termini generali, risolvendo il modello di mercato per il prezzo di equilibrio, si ottiene:
Questa è un’equazione alle differenze finite del primo ordine (➔ differenze finite), la cui soluzione generale è
dove
è la soluzione stazionaria – determinata dalla condizione pt=pt−1 di invarianza del prezzo nel tempo – e p0 il prezzo iniziale diverso da p*. Questa soluzione descrive l’andamento del prezzo nel corso del tempo, dato lo scostamento iniziale dalla soluzione stazionaria. Poiché il termine
assume alternativamente valori positivi e negativi, la soluzione presenta andamento oscillatorio: il prezzo di equilibrio si discosta in eccesso e in difetto del valore stazionario. Si ottengono così oscillazioni di ampiezza divergente, costante o convergente, rispettivamente se
è minore, uguale o maggiore di −1, le cui rappresentazioni grafiche (figure. B, C e D) mostrano il sentiero percorso dal prezzo nelle successive posizioni di equilibrio del mercato. I casi, in particolare, di oscillazioni divergenti e convergenti danno ragione del termine ‘ragnatela’, coniato da Kaldor per descrivere la dinamica del prezzo. Studi successivi hanno attenuato il rischio di soluzioni divergenti, sostituendo alle aspettative statiche ipotesi meno rigide quali, per es., quelle di aspettative adattive e razionali (➔ aspettativa).
