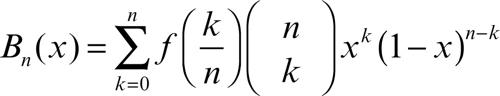Weierstrass, teorema di approssimazione polinomiale di

Weierstrass, teorema di approssimazione polinomiale di

Weierstrass, teorema di approssimazione polinomiale di in analisi, stabilisce che una funzione ƒ continua in un intervallo [a, b] può essere approssimata uniformemente mediante polinomi. Astrattamente: il sottospazio dei polinomi è denso in C⁰([a, b]). Una successione approssimante la funzione ƒ(x) in [0, 1] è data dai polinomi di → Bernštein,

Volendo, i polinomi possono essere sempre pensati a coefficienti razionali. Il teorema si estende a funzioni continue su un dominio chiuso e limitato di Rⁿ e mostra quindi che i polinomi sono sufficienti ad approssimare uniformemente le funzioni continue.