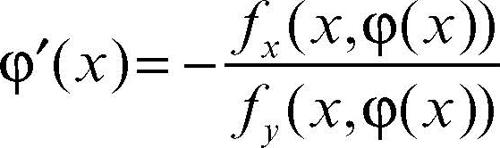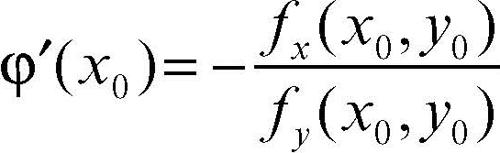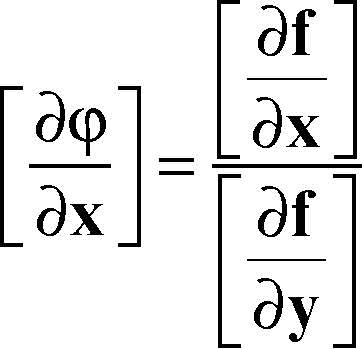Dini, teorema di
Dini, teorema di
Dini, teorema di in analisi, stabilisce che se una funzione reale di due variabili ƒ(x, y) è continua con la sua derivata parziale ƒy in un aperto A di R2, se P0(x0, y0) ∈ A e se la funzione si annulla in P0 mentre la sua derivata parziale ƒy è diversa da 0 in tale punto, cioè ƒ(x0, y0) = 0 e ƒy(x0, y0) ≠ 0, allora l’equazione ƒ(x, y) = 0 è univocamente risolubile rispetto a y in un intorno di P0 e la funzione implicita φ(x) da essa definita è continua in U. Se inoltre anche la derivata parziale ƒx è continua, φ(x) è derivabile e risulta
In particolare, essendo φ(x0) = y0, è esplicitamente calcolabile la derivata
Se poi ƒ ∈ Cn(A), anche φ ∈ Cn(U) e le derivate successive si possono calcolare applicando ripetutamente la formula di derivazione delle funzioni composte all’identità ƒ(x, φ(x)) ≡ 0. Il teorema si generalizza a funzioni di più variabili, anche vettoriali, e quindi a sistemi (si hanno anche generalizzazioni in spazi di Banach). Il sistema f(x, y) ≡ 0, con x ∈ Rm, y ∈ Rn e f: Rn+m → Rn di classe C1 è univocamente risolubile rispetto a y in un intorno di una sua radice se il determinante jacobiano parziale det(Jy) = ∂f/∂y non si annulla nella radice; la matrice jacobiana del vettore φ(x) definito dall’identità f(x, φ(x)) ≡ 0 è data da