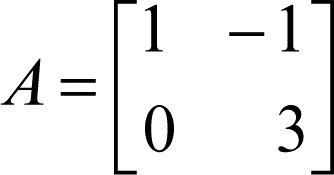Hamilton-Cayley, teorema di
Hamilton-Cayley, teorema di
Hamilton-Cayley, teorema di in algebra lineare, stabilisce che se ƒ è un endomorfismo di uno spazio vettoriale Vn su un campo K e p(x) è il polinomio caratteristico associato alla matrice che lo definisce, allora p(ƒ) = 0. In modo analogo, se A è una matrice quadrata di ordine n con elementi in un campo K e p(x) il polinomio caratteristico a essa associato, risulta p(A) = 0. La seconda proposizione risulta vera anche per matrici quadrate con elementi in un anello commutativo. Data per esempio la matrice
il cui polinomio caratteristico è p(x) = x 2 − 4x + 3, in virtù del teorema si ha A2 − 4A + 3I2 = 0; in altri termini, ogni matrice annulla il proprio polinomio caratteristico. Dal teorema discende il seguente corollario: il polinomio minimo di un endomorfismo ƒ di uno spazio vettoriale Vn divide il suo polinomio caratteristico.