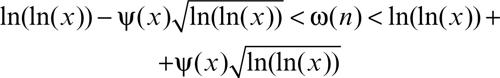Hardy, teorema di
Hardy, teorema di
Hardy, teorema di denominazione con cui si indicano diversi risultati ottenuti da G.H. Hardy nei primi anni del Novecento. Uno dei principali, dimostrato da Hardy nel 1914, riguarda la funzione zeta di → Riemann e stabilisce che tale funzione ammette un’infinità di zeri la cui parte reale è uguale a 1/2. Il teorema è parte dell’ipotesi di → Riemann, uno dei → problemi del millennio, tuttora (2013) indimostrata, secondo cui tutti gli zeri della funzione hanno parte reale uguale a 1/2. Il teorema può anche essere formulato affermando che sulla retta critica si trova un’infinità di zeri non banali della funzione di Riemann, dove per retta critica si intende la retta che nel piano complesso unisce tutti i punti che rappresentano numeri s con parte reale uguale a 1/2; in simboli Re(s) = 1/2. Altro risultato importante riportato come teorema di Hardy o come teorema di Hardy-Ramanujan riguarda anch’esso la distribuzione dei numeri primi e stabilisce che se ω(n) è il numero di fattori primi distinti di n e se ψ(x) tende uniformemente a infinito per x tendente a infinito, allora valgono le seguenti disuguaglianze
per quasi tutti i numeri n < x, dove l’espressione «quasi tutti» significa che la frequenza di naturali n nell’intervallo 1 ≤ n ≤ x per i quali
tende a 0 per x tendente a infinito.