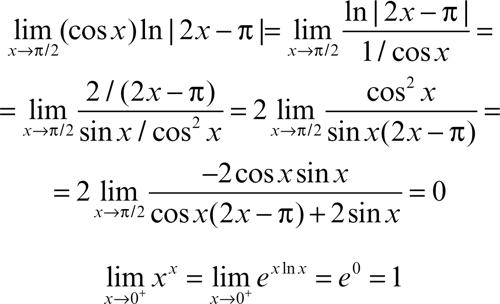L'Hopital (de), teorema di
L'Hopital (de), teorema di
L’Hôpital (de), teorema di o regola di de L’Hôpital, procedimento utile per il calcolo di limiti di forma indeterminata dei tipi 0/0 e ∞/∞. Il teorema stabilisce che se per x → x0 il quoziente di due funzioni, ƒ(x)/g(x), assume la forma indeterminata 0/0 o ∞/∞ e il quoziente delle rispettive derivate, ƒ′ (x)/g′ (x), ammette limite l, allora anche il quoziente ƒ(x)/g(x) ammette limite l per x → x0. Per esempio:
La condizione non è necessaria: per esempio, il rapporto (x + cosx)/x tende a 1 per x → ∞, ma il rapporto delle derivate non ammette limite.
Le altre forme indeterminate si possono ricondurre a una delle due sopraindicate con le trasformazioni indicate simbolicamente da 0 = 1/∞ o ∞ = 1/0 per la forma 0 ⋅ ∞ e da ƒ g = eglnƒ per le forme 1∞, 00 e ∞0. Il caso ∞ − ∞ si riduce a ∞ ⋅ 0 (o a una espressione non indeterminata) se si può raccogliere un fattore comune ai due termini. Per esempio:
La regola è molto comoda per forme indeterminate piuttosto semplici, mentre nei casi più complessi, nei quali i due infinitesimi (o infiniti) sono di ordine elevato, è preferibile utilizzare le scale di infiniti e infinitesimi utilizzando la nozione di equivalenza asintotica.