Lagrange, teorema di (per una derivata)
Lagrange, teorema di (per una derivata)
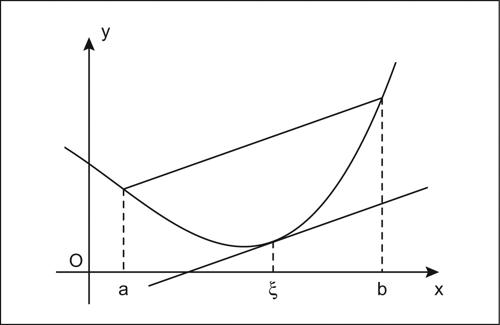
Lagrange, teorema di (per una derivata) stabilisce che, se ƒ(x) è una funzione continua in un intervallo [a, b] e derivabile nell’intervallo aperto (a, b), esiste almeno un punto ξ ∈ (a, b) in cui
Geometricamente, nell’arco descritto da ƒ(x) in [a, b] esiste almeno un punto in cui la tangente è parallela alla corda che ne congiunge gli estremi. Sue conseguenze immediate sono:
• se ƒ(x) ha derivata nulla in tutto (a, b), essa è costante;
• due primitive di una stessa funzione differiscono per una costante.
Se ƒ(b) = ƒ(a) questo teorema si riduce a quello di → Rolle, dal quale viceversa si può dedurre considerando la funzione
Il teorema si generalizza a derivate di ordine superiore (→ Lagrange, resto di).
Con riferimento all’intervallo [x, x + h], il teorema si scrive nella forma ƒ(x + h) = ƒ(x) + h ƒ′′(x + θh), con 0 < θ < h, e permette di stimare quanto ƒ(x + h) si discosta dal valore noto in un punto x. L’errore commesso sostituendo ƒ(x) a ƒ(x + h) infatti non supera in modulo Mh, essendo M il massimo modulo della derivata in [x, x + h]. Per esempio, se ƒ(x) = √(x), il valore di √(123) differisce da √(121) = 11 per non più di
Infatti √(123) = 11,0905365…
Il punto ξ ∈ (121, 123) in cui vale l’uguaglianza
è dato da
Analogamente al caso del teorema per un integrale definito, questo teorema è anche detto teorema della media o teorema del valore medio. Il teorema puo essere considerato come un caso particolare del teorema di Cauchy (per questo alcuni autori lo riportano come secondo teorema del valor medio). Inoltre è anche noto come teorema di Cavalieri-Lagrange in quanto fu esposto in forma geometrica da B. Cavalieri.