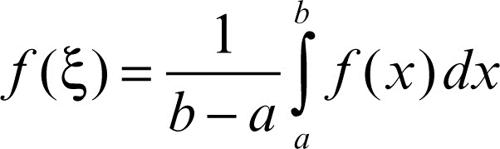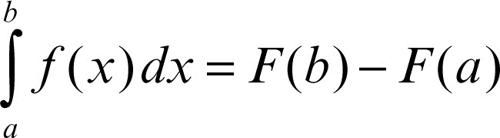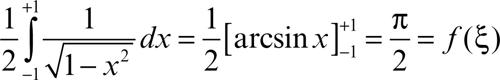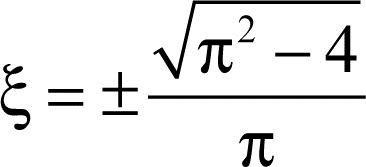Lagrange, teorema di (per un integrale definito)
Lagrange, teorema di (per un integrale definito)
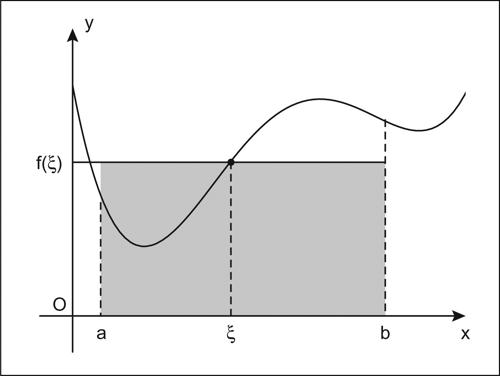
Lagrange, teorema di (per un integrale definito) in analisi, stabilisce che per una funzione ƒ(x) continua in un intervallo [a, b], esiste (almeno) un punto ξ ∈ (a, b) in cui tale funzione ƒ assume il suo valor medio in [a, b]:
Questo teorema, detto anche teorema della media integrale o teorema del valore medio integrale, equivale al corrispondente risultato per la derivata, in virtù del fatto che
con F primitiva di ƒ(x). Il teorema si estende anche agli integrali impropri, purché le discontinuità siano solo agli estremi dell’intervallo (a, b). Per esempio, la funzione
è integrabile in [−1, 1], e risulta
per
Invece la funzione integrabile ƒ(x) = x−1/3 ha integrale nullo in [−1, 1] perché la funzione è dispari (e quindi le due aree con segno, sottese negli intervalli [−1, 0) e (0, +1], sono uguali in valore assoluto, ma si annullano perché di segno opposto), ma non si annulla mai.