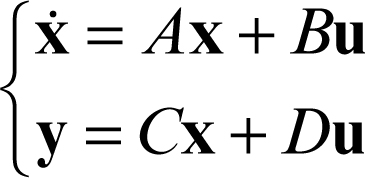Ljapunov, teorema di

Ljapunov, teorema di

Ljapunov, teorema di in analisi, asserisce che la stabilità di un sistema dinamico a tempo continuo, lineare a tempo invariante, espresso dal sistema di equazioni

è collegata agli autovalori λ_k della matrice quadrata A (con k = 1, …, n, dove n è l’ordine del sistema). Più precisamente: a) se Re(λ_k) ≤ 0 per k = 1, …, n, il sistema è stabile; b) se Re(λ_k) < 0 per k = 1, …, n, il sistema è asintoticamente stabile; c) se Re(λ_k) > 0 per almeno un valore di k, il sistema è instabile (→ sistema dinamico).

□ In statistica, è a volte riportato con tale denominazione il teorema del → limite centrale.