Menelao, teorema di
Enciclopedia della Matematica (2013)
Menelao, teorema di
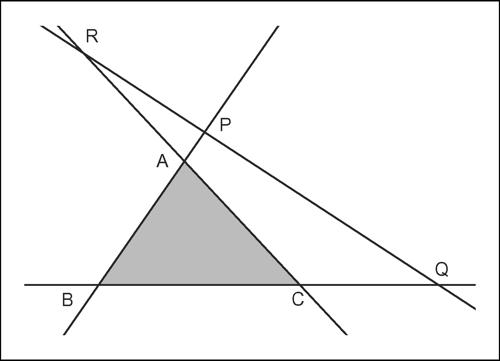
Menelao, teorema di stabilisce che i punti P, Q e R, appartenenti rispettivamente ai lati AB, BC e CA di un triangolo ABC o ai loro prolungamenti, sono allineati se e solo se risulta verificata la seguente condizione:
Nel teorema si tiene conto del fatto che le misure di due segmenti paralleli sono considerate di segno concorde se il verso che porta dal primo estremo al secondo è lo stesso per entrambi i segmenti, di segno discorde in caso contrario. Il teorema di Menelao è in relazione duale con il teorema di → Ceva. Mentre il primo fornisce un criterio per la collinearità di tre punti, il secondo dà un criterio per la concorrenza di tre rette in un punto.