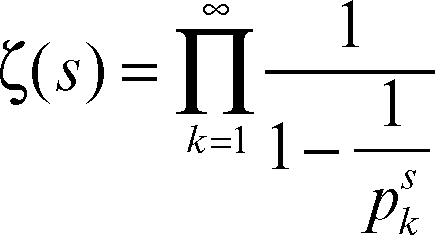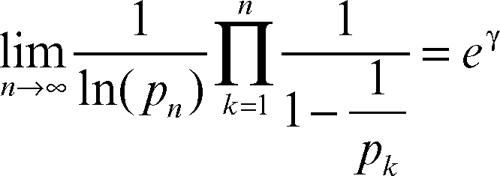Mertens, teorema di

Mertens, teorema di

Mertens, teorema di denominazione con cui si indica un particolare risultato ottenuto da F. Mertens relativo alla funzione zeta di → Riemann ζ(s). Per l’espressione di tale funzione come prodotto di → Eulero

dove p_k è il k-esimo numero primo, si ha ζ(1) = ∞. Tuttavia, se si considera il prodotto finito fino a k = n, lo si moltiplica per 1/ln(p_n) e si fa tendere n a infinito, si ottiene la seguente relazione (nota, appunto come teorema di Mertens):

dove γ è la costante di Eulero-Mascheroni (→ Eulero, costante di). Approssimato a meno di 10⁻⁶, tale valore è 1,781072.