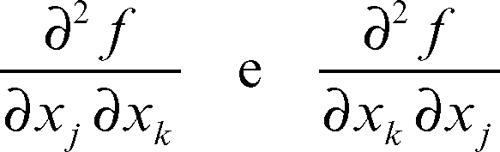Schwarz, teorema di
Enciclopedia della Matematica (2013)
Schwarz, teorema di
Schwarz, teorema di (per le derivate parziali) in analisi, stabilisce che se una funzione di più variabili ƒ(x1, x2, …, xn) ha le derivate seconde miste
continue, esse sono uguali. Ne segue che la matrice hessiana di una funzione di classe C 2 è simmetrica (→ funzione di classe Cn). Per la validità della tesi è sufficiente supporre che una delle due derivate sia continua e l’altra esista.