Steiner, teorema di

Steiner, teorema di

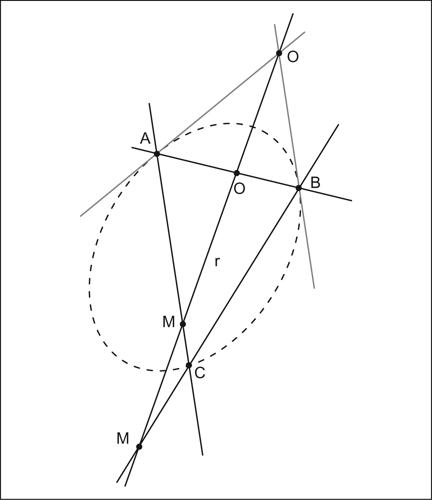
Steiner, teorema di in geometria proiettiva, teorema che riguarda la generazione proiettiva delle coniche non degeneri. Afferma che ogni conica del piano può essere ottenuta come luogo dei punti in cui si intersecano due rette corrispondenti di due fasci proiettivi. Se i fasci sono prospettivi o sovrapposti, la conica è degenere.

Sotto la denominazione di teorema di Steiner sono annoverati anche altri teoremi, tra i quali quello che risolve il problema della costruzione di una rete minimale a partire da tre punti. Tale teorema stabilisce che il punto P del piano che rende minima la somma AP + BP + CP delle sue distanze da tre punti non allineati A, B, C dello stesso piano è il punto che vede sotto un angolo di 120° ciascuno dei tre lati del triangolo ABC, a condizione che nessuno dei suoi angoli sia maggiore o uguale a 120°. Se tale condizione non si verifica il punto P richiesto coincide con il vertice dell’angolo ottuso.