Euclide, teoremi di

Euclide, teoremi di

Euclide, teoremi di nella geometria del piano sono così detti due teoremi che costituiscono, insieme al teorema di Pitagora, i teoremi fondamentali relativi ai triangoli rettangoli.

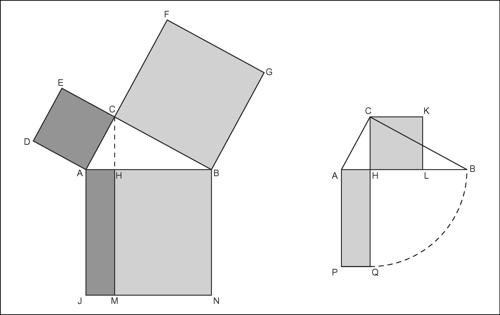
Il primo teorema di Euclide stabilisce che, in un qualsiasi triangolo rettangolo, il quadrato costruito su uno dei cateti è equivalente (nel senso di equiesteso) al rettangolo che ha per lati l’ipotenusa e la proiezione su di essa del cateto considerato. Con riferimento alla figura, esso stabilisce che

Poiché AB = AJ = BN le due relazioni precedenti possono anche essere scritte in queste forme equivalenti:

che evidenziano il fatto che in un qualsiasi triangolo rettangolo un cateto è medio proporzionale fra l’ipotenusa e la sua proiezione sull’ipotenusa.

Il secondo teorema di Euclide stabilisce che, in un qualsiasi triangolo rettangolo, il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per dimensioni le proiezioni dei cateti sull’ipotenusa. Con riferimento alla figura, esso stabilisce che

o, con scrittura equivalente, che

scrittura che evidenzia il fatto che in un qualsiasi triangolo rettangolo l’altezza relativa all’ipotenusa è media proporzionale fra le proiezioni dei due cateti sull’ipotenusa.

I teoremi di Euclide permettono quindi di costruire un quadrato equivalente a un rettangolo. Poiché si può facilmente dimostrare che dato un qualunque poligono si può costruire un rettangolo a esso equivalente, i due teoremi permettono di definire l’area di un qualunque poligono come l’area del quadrato a esso equivalente e di assumere quindi il quadrato come la figura di riferimento per l’unità di misura delle superfici.