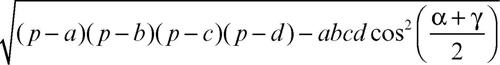Eulero, teoremi di

Eulero, teoremi di

Eulero, teoremi di (per un quadrilatero) nella vasta produzione di Eulero ci sono due teoremi, a lui attribuiti, che riguardano le proprietà di un quadrilatero. Uno di essi stabilisce che la somma dei quadrati dei lati di un quadrilatero equivale alla somma dei quadrati delle diagonali aumentata di quattro volte il quadrato del segmento congiungente i punti medi delle diagonali.

Un altro teorema riguarda l’area di un quadrilatero qualunque e stabilisce che l’area di un quadrilatero convesso di lati a, b, c, d è uguale a

dove p è il semiperimetro del quadrilatero e α e γ sono le ampiezze di due suoi angoli opposti. Nel caso in cui il quadrilatero sia inscrivibile in una circonferenza si ha (α + γ)/2 = π/2 e quindi il coseno è nullo. Si ricava pertanto che l’area di un quadrilatero inscrivibile in una circonferenza è

formula già nota al matematico indiano del sec. vii Brahmagupta. Se il quadrilatero si riduce a un triangolo e quindi uno dei lati, per esempio d, ha misura nulla, si ritrova come caso particolare la formula di Erone per l’area dei triangoli (→ Erone formula di).