Pappo, teoremi di

Pappo, teoremi di

Pappo, teoremi di denominazione relativa a vari teoremi di geometria, tra i quali i due che seguono sono i più significativi.

Teorema armonico di Pappo

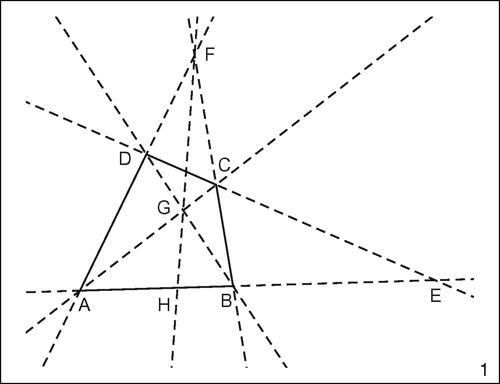
Il teorema stabilisce che in un quadrilatero completo (quadrangolo completo) di vertici A, B, C, D, in cui G è il punto d’intersezione delle sue diagonali, ciascun lato è diviso armonicamente dalle rette passanti per G e condotte dai punti E e F in cui si intersecano i prolungamenti dei lati. Per esempio, con riferimento alla figura, i punti A e B, H ed E costituiscono una quaterna armonica, cioè risulta uguale a −1 il birapporto (A, B, H, E).

Teorema di Pappo sugli esagoni

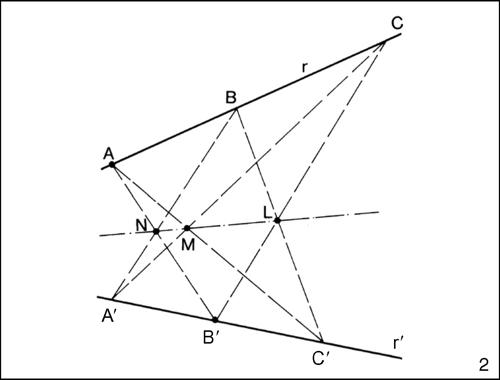
Il teorema (caso particolare del teorema di → Pascal) stabilisce che se A, B, C sono tre punti su un retta r e A′, B′, C′ sono tre punti su una retta r′, indicati con L l’intersezione delle rette BC′ e B′C, con M le intersezioni delle rette AC′ e A′C, con N le intersezioni delle rette AB′ e A′B, i punti L, M, N sono allineati. La configurazione che risulta è anche detta esagramma mistico. Tale teorema, detto anche teorema di Pappo-Pascal, è un teorema autoduale (→ dualità).