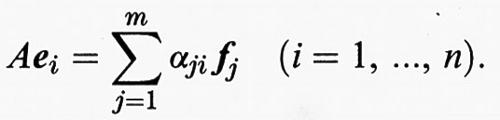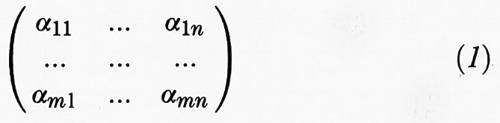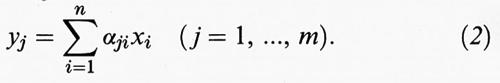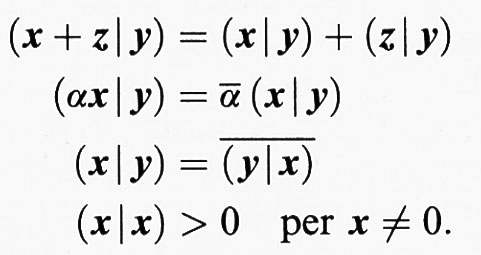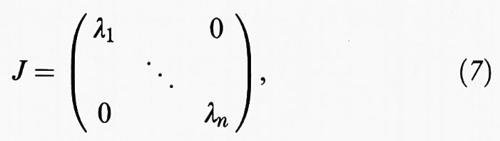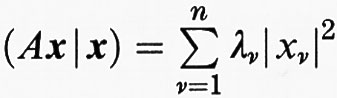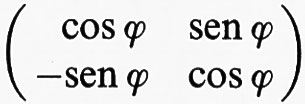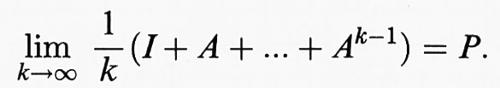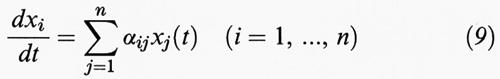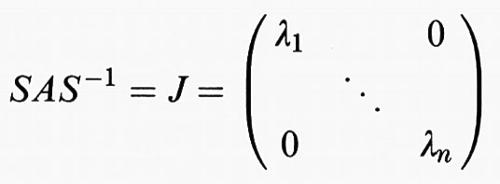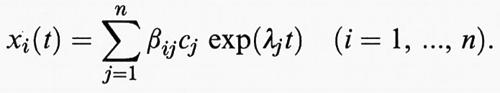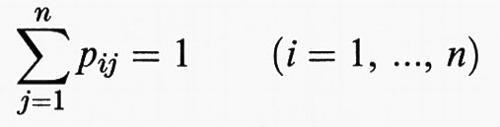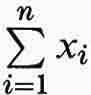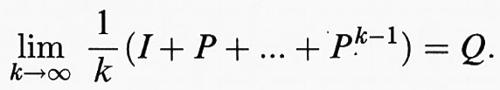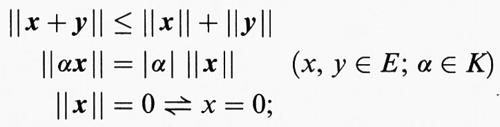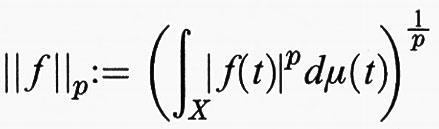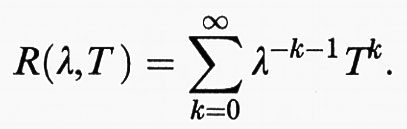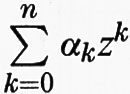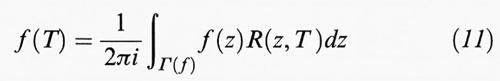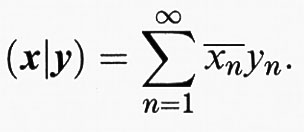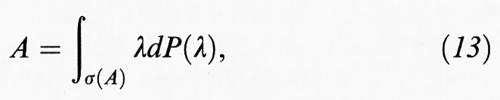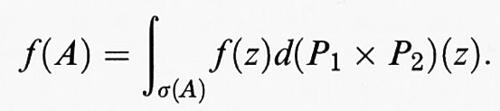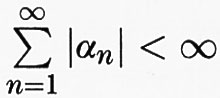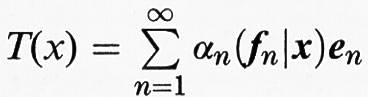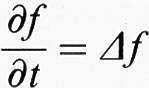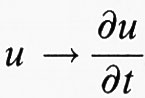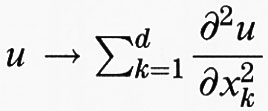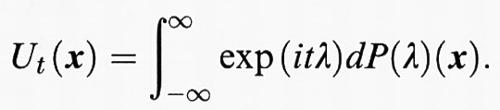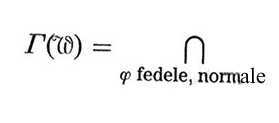Operatori, teoria degli
Operatori, teoria degli
Sommario: 1. Introduzione. 2. Operatori lineari fra spazi di dimensione finita. a) Generalità. b) Operatori hermitiani, normali e unitari. c) Operatori lineari positivi. d) Esempi di applicazioni. 3. Operatori su spazi di Banach. a) Operatori lineari limitati. b) Spettro e calcolo funzionale. c) Operatori compatti. d) Operatori hermitiani, normali e unitari. e) Operatori positivi su reticoli di Banach. 4. Operatori illimitati. a) Introduzione. b) spettro. c) Operatori speciali. d) Semigruppi a un parametro e il problema astratto di Cauchy. 5. Algebre di operatori. a) Introduzione. b) W*-algebre; c) prospettive. □ Bibliografia.
1. Introduzione
La teoria degli operatori lineari - o, in breve, teoria degli operatori - abbraccia uno dei campi più vasti dell'analisi moderna. Essa si è sviluppata in maniera ininterrotta durante tutto il XX secolo, soprattutto per quel che riguarda gli operatori sugli spazi di Hilbert; tuttavia, le conoscenze fondamentali, relativamente agli spazi di dimensione finita e in particolare alla teoria delle matrici quadrate, risalgono al XIX secolo, e a questi importanti casi speciali verrà dedicata la prima parte del presente articolo. Verrà quindi presa in esame la teoria degli operatori, limitati e illimitati, su spazi di Banach, che sono risultati fondamentali per l'intera analisi moderna; infine forniremo alcuni cenni riguardo alla teoria delle algebre di operatori. (Per una più estesa trattazione di argomenti correlati, v. analisi, vol. I; v. equazioni funzionali, vol. II).
2. Operatori lineari fra spazi di dimensione finita
a) Generalità
Siano dati due spazi vettoriali (detti anche: spazi lineari) E, F sul corpo scalare K; in seguito sarà sempre supposto K = R o K = C (corpo numerico reale o complesso, rispettivamente). Una ‛base' (più precisamente: base di Hamel) di uno spazio lineare è un sistema massimo B di elementi dello spazio linearmente indipendenti; ogni spazio vettoriale possiede almeno una base (secondo il lemma di Zorn) la cui cardinalità è univocamente determinata e si dice ‛dimensione' dello spazio vettoriale. Se questa è un numero naturale n ∈ N, lo spazio vettoriale si dice ‛di dimensione finita'. Un'applicazione A : E → F si dice ‛lineare', ovvero si parla di ‛operatore lineare' (in seguito, brevemente, operatore), qualora sia verificata la condizione: A (αx + βy) = αAx + βAy (x, y ∈ E; α, β ∈ K).
Siano ora E, F di dimensione finita rispettivamente n e m, e B1 = {e1, ..., en} e B2 = {f1, ..., fm} rispettivamente basi di E e di F. L'operatore A, evidentemente, è completamente definito quando se ne conosce l'effetto sul generico elemento ei della base B1 ∈ E:
I coefficienti αji risultano univocamente determinati e formano una matrice rettangolare di numeri di K:
che spesso (conoscendo B1 e B2) viene identificata con l'operatore A. Se (x1, ..., xn) sono le componenti di x ∈ E relative a B1 e (y1, ..., ym) quelle di y = Ax relative a B2, l'effetto di A sarà completamente descritto dall'equazione
In linea di principio si può impiegare per la descrizione di A : E → F una qualsivoglia base di E e rispettivamente di F; specialmente nel caso in cui E = F, si può spesso, attraverso la giusta scelta della base, porre in evidenza particolari proprietà di A. Sia ora E = F (di conseguenza m = n) e K = C. Allora esiste sempre una base B che si può pensare di dividere in k (1 ≤ k ≤ n) blocchi Bκ = eκ1, ..., eκnκ e relativamente alla quale la matrice (1) prenderà la forma seguente:
in cui ogni Jκ (κ = 1, ..., k) è della forma semplice seguente,
Siano ora fissati κ (1 ≤ κ ≤ k) e il vettore zκ, il quale relativamente al blocco Bκ possiede le componenti (1, 0, ..., 0) e relativamente a tutti i rimanenti blocchi Bλ (λ ≠ κ) ha componenti nulle; dalla (2) e dalla (4) segue che vale Azκ = ακzκ con zκ ≠ 0. Un numero λ ∈ K, per il quale l'equazione λz = Az è risolubile con z ≠ 0, si dice un ‛autovalore' di A e la (3) è la ‛forma normale di Jordan' di A. Dalla (4) risulta inoltre che i numeri ακ (κ = 1, ..., k) sono tutti autovalori di A; sicuramente non c'è bisogno che siano tutti diversi (basti pensare all'applicazione identica - operatore unità - I : E → E). Quindi, nel caso in cui K = C ogni operatore A : E → E (n ≥ q 1) ha almeno un autovalore.
Si riferisca A, secondo la (1), a una qualsivoglia base B di E; il determinante det (λI - A) =: p(λ) è allora un polinomio in λ (indipendente da B) ed è detto ‛polinomio caratteristico' di A. Come si può desumere dalla (3), gli autovalori di A sono proprio le radici (generalmente complesse) di questo polinomio. Quindi vale il seguente teorema di Cayley-Hamilton: ogni operatore A annulla il suo polinomio caratteristico, vale cioè p (A) = 0 (si scrive p (A) poiché si sostituisce in p (λ) a λν la potenza Aν, che viene calcolata tramite la moltiplicazione fra matrici o fra operatori). Si noti che p (λ) non è necessariamente il polinomio di grado più piccolo che annulla A; quest'ultimo (con il coefficiente di ordine massimo uguale a 1) è univocamente determinato, è chiamato ‛polinomio minimo' m (λ) di A ed è un divisore di p (λ). Un semplice esempio: la matrice
,
interpretata come operatore su 2 con base B = {(1, 0), (0, 1)}, è già nella forma normale di Jordan; ha un unico autovalore 1 con autovettore (1, 0). Per essa si ha p (λ) = m (λ) = (λ - 1)2. Per la matrice identica I =
si ha invece p (λ) = (λ - 1)2, m (λ) = λ - 1.
La totalità degli autovalori di A si dice spettro σ (A) di A. Per dim E = n ≥ 1, K = C, σ (A) consiste di almeno uno e al massimo di n numeri α ∈ C. Per K = R può essere che risulti σ (A) = ∅, come mostra l'esempio (x, y) → (y, x). Infine indichiamo con ρ (A) = Cσ (A) l'‛insieme risolvente' di A; infatti per λ ∈ ρ (A), esiste l'inversa (λ - A)-1, cioè è sempre e univocamente risolubile l'equazione λx - Ax = y. Sia ora A : Cn → Cn un qualsivoglia operatore con spettro σ (A): chiameremo r (A) = max {∣λ∣: λ ∈ σ (A)} ‛raggio spettrale' di A e la circonferenza {z ∈ C: ∣z∣ = r (A)} ‛circonferenza spettrale'. Per λ ∈ ρ (A), (λ - A)-1 non può essere ulteriormente esplicitato; però, per ∣λ∣ > r (A), vale lo sviluppo in serie
Formula
per il ‛risolvente' (la cosiddetta ‛serie di Neumann'). Allorché gli operatori su Cn vengono identificati da matrici, queste possono essere viste come elementi di Cn2; anche in questo caso il limite è il consueto valore limite sullo spazio Cn2.
b) Operatori hermitiani, normali e unitari
La forma più semplice della forma normale di Jordan (3) di un operatore A : E → E (E di dimensione finita) si ha quando i blocchi di Jordan Bκ (κ = 1, ..., k) hanno tutti lunghezza 1; in tal caso risulta k = n ed esiste una base di E che è costituita solo di autovettori. Condizione necessaria e sufficiente perché ciò accada è che il polinomio minimo m (λ) sia costituito solo da fattori lineari; il suo grado è allora il numero dei differenti autovalori di A. Tuttavia, nelle applicazioni, soprattutto in fisica e in particolare in meccanica, si arriva a tali operatori per un'altra via, cioè attraverso i concetti di prodotto interno e di metrica euclidea. Per prodotto interno (prodotto scalare) di E si intende un'applicazione (x, y) → (x ∣ y) di E × E in K, per cui valgono le condizioni:
Queste devono valere per tutti gli x, y, z ∈ E e α ∈ K; per K = C, con ᾱ si intende il numero complesso coniugato di α. Vengono definite su E una norma, ponendo ∥x∥ = (x ∣ x)1/2, e una metrica, con d (x, y) = ∥x - y∥, che viene chiamata ‛metrica euclidea'. Uno spazio di dimensione n dotato di questa metrica (e norma) si dice per K = R ‛spazio euclideo', per K = C ‛spazio unitario' di dimensione n (∈ N).
Sia ora nel seguito E unitario, dim E = n. Due sottoinsiemi M, N di E si dicono ‛ortogonali' nel caso in cui (x ∣ y) = 0 per ogni x ∈ M, y ∈ N. In particolare, diremo anche che gli elementi x ∈ M, y ∈ N sono ortogonali. Un ‛sistema ortogonale' è un sottoinsieme Q, per il quale si ha che per x ∈ Q, y ∈ Q e x ≠ y, posto x ≠ 0, y ≠ 0, è (x ∣ y) = 0; si parla di ‛sistema ortonormale' quando in più vale x ∈ Q → ∥x∥ = 1. Sia ora A : E → E un operatore (lineare); con l'identità
(Ax∣y) = (x∣A*y) (x, y ∈ E) (6)
si definisce un altro operatore A*, che si indicherà come ‛aggiunto di A' (o come aggiunto ad A).
Per quanto riguarda l'applicazione A → A* valgono le seguenti regole: (A + B)* = A* + B*, (AB)* = B* A*, A** = A e (αA)* = ᾱA*. In particolare, nel caso in cui A = A* l'operatore viene detto ‛autoaggiunto' o ‛hermitiano'. Sia B una base ortonormale di E e A = (αij) (v. 1) la matrice corrispondente ad A, allora l'operatore autoaggiunto A = A* è espresso attraverso αij = ᾱji (i, j = 1, ..., n); in particolare una matrice simmetrica reale (αij = αji) definisce sempre un operatore hermitiano se è riferita a una base ortonormale di E.
Dalla (6) segue facilmente che gli autovalori di un operatore hermitiano sono sempre reali; ma vale il seguente più ampio teorema di trasformazione ad assi principali di un operatore hermitiano, che mette in evidenza il significato degli operatori hermitiani (e in particolare di quelli reali e simmetrici): per ogni operatore hermitiano A : E → E esiste una base ortonormale B di E, che è composta solo da autovettori; gli autovalori di A sono tutti reali. Questo significa che la forma normale di Jordan (3) di A assume la forma
quindi è una matrice diagonale reale; gli autovalori λν (ν = 1, ..., n) non sono necessariamente diversi (operatore identità!). La cosiddetta ‛forma quadratica' x → (Ax ∣ x) ha, riferita alla base B, la forma canonica
(sostanzialmente univoca solo nel caso di λν diversi). Sia ora B = y1, ..., yn una tale base e Pν l'operatore definito da Pνyν = yν e Pνyμ = 0 (μ ≠ ν) per μ, ν = 1, ..., n. Allora dalla (7) segue che:
Ogni Pν è un operatore che soddisfa le equazioni P2 = P e P = P* e viene detto ‛proiezione ortogonale' poiché E = P(E) + P-1(0) fornisce una decomposizione ortogonale di E. Le proiezioni ortogonali sono operatori hermitiani molto particolari, in quanto, come mostra la (8), costituiscono gli elementi che permettono di costruire tutti gli operatori hermitiani. Si osserva ancora che per μ ≠ ν vale sempre PμPν = 0.
Per un qualunque operatore A si definiscono gli operatori hermitiani B, C scrivendo B = (1/2) (A+A*), C = (1/2i) (A-A*) e pertanto segue immediatamente (i2 = -1) che A = B + iC. Questa idea è utile, però, solo quando B e C commutano (cioè quando è BC = CB). Ciò è evidente quando vale AA* = A*A; gli operatori di questo tipo si dicono ‛normali' e costituiscono una generalizzazione degli operatori hermitiani con molte proprietà simili: per un operatore normale valgono tutte le asserzioni del teorema degli assi principali, con la sola eccezione che gli autovalori λν (ν = 1, ..., n) non sono necessariamente reali. In particolare valgono anche le equazioni (7) e (8). Una classe speciale, molto importante, di operatori normali è costituita dagli operatori ‛unitari', che sono caratterizzati dall'equazione UU* = I. Poiché, a causa della dimensione finita di E, è anche U*U = I, segue che U* = U-1. Come mostra immediatamente la (7), un operatore normale A è unitario quando risulta per tutti gli autovalori ∣λν∣ = 1. Con l'aiuto del prodotto interno si può riconoscere che per un operatore unitario vale sempre (x ∣ x) = (U*Ux ∣ x) = (Ux ∣ Ux) per ogni x∈ E; segue anche che ∥x∥ = ∥Ux∥. Gli operatori unitari sono dunque esattamente le isometrie lineari dello spazio unitario E, con la metrica d (x, y) = ∥x - y∥. Da ciò segue che per ogni due basi ortonormali di E è univocamente determinato un operatore unitario che associa a ogni elemento di una base l'elemento corrispondente dell'altra; viceversa, ogni operatore unitario copia una qualsivoglia base ortonormale di E in un'altra dello stesso tipo. Un esempio semplice è dato da
per ϕ ∈ R, che descrive la rotazione dello spazio euclideo R2 di ϕ gradi in senso positivo.
c) Operatori lineari positivi
Sia E un qualsivoglia spazio vettoriale su R o su C e sia dim E = n ∈ N allora, attraverso la scelta di elementi x ∈ E di una qualsivoglia (ma da ora in poi fissata) base di E, si può porre un isomorfismo con lo spazio Rn o Cn; noi perciò in seguito ci limiteremo a Rn e rispettivamente a Cn. Per gli elementi x = (x1, ..., xn) si definisce un ordinamento (parziale) ponendo: x ≤ y ⇋ xν ≤ yν (ν = 1, ..., n), naturalmente se xν ∈ R, yν ∈ R per ogni ν = 1, ..., n. Per i vettori reali x, y la disequazione x ≤ y ha lo stesso significato di y - x ≥ 0. Un operatore A di Cn, che trasforma Rn in se stesso e perciò possiede una matrice reale A = (αij), si dice ‛positivo' e si scrive A ≥ 0, quando per x ≥ 0 segue sempre Ax ≥ 0. Pertanto A ≥ 0 è equivalente a αij ≥ 0 (ij = 1, ..., n). Sulla classe di questi operatori, benché abbia minor rilievo rispetto a quella degli operatori normali (v. cap. 2, § b), è stata tuttavia elaborata un'interessante teoria, della quale vogliamo dare una breve idea. Facciamo notare che nella teoria degli operatori hermitiani viene qualche volta indicato come positivo un operatore quando per tutti i suoi autovalori λν (ν = 1, ..., n) vale λν ≥ 0: ciò sta in rapporto solo molto alla lontana con la positività qui considerata.
In base alla (5) si può supporre che λ → R(λ, A) sia una funzione analitica (olomorfa) nell'insieme risolvente Cρ(A); le sue singolarità, che costituiscono lo spettro di A, formano, nel caso in cui dim E = n ∈ N, un insieme finito di poli. L'ordine di questi poli non è altro che la molteplicità delle corrispondenti radici del polinomio minimo. Si ha il seguente teorema (Frobenius): per ogni operatore positivo A su Cn, il raggio spettrale r(A) è un autovalore con un autovettore x ≥ 0; nel caso in cui r(A) > 0, r(A) è il polo di R(λ, A) di ordine massimo sul cerchio spettrale; inoltre, se r(A)ε, (∣ε∣ = 1) è un autovalore di A, lo è anche ogni numero r(A)εk (k intero). Nel caso in cui r = r(A) > 0 ci si può ricondurre, attraverso la considerazione di r-1A, su r = 1; allora dal suddetto teorema segue che la parte dello spettro (detto spettro periferico) che è sul cerchio spettrale ∣λ∣ = 1 è costituita dall'unione di gruppi di radici dell'unità. Per il raggio spettrale r(A) vale la seguente facile valutazione: s ≤ r(A) ≤ t, dove s è la più piccola e t la più grande delle somme delle righe di A; analogamente per la somma delle colonne.
Un operatore A si dice ‛ergodico in media' se esiste il limite
Qui P è un operatore ‛idempotente', cioè tale che P2 = P, il quale sarà indicato anche come proiezione di E su P (E) (con nucleo (I - P)E). Per l'ergodicità in media vale inoltre il seguente teorema: sia A ≥ 0 e r (A) = 1; allora le seguenti affermazioni sono equivalenti: a) λ = 1 è un polo semplice del risolvente; b) la sequenza (Ak)k ∈ N delle potenze di A è limitata su Cn2; c) A è ergodico in media. Per gli operatori ergodici in media, P è sempre una proiezione sullo spazio dei vettori fissi di A, che soddisfa AP = PA = P. Per A ≥ 0 si ha inoltre che 0 ≠ P = limk→∞ Ak, precisamente quando r (A) = 1 e λ = 1 è l'unico autovalore sul cerchio spettrale.
d) Esempi di applicazioni
Per illustrare l'applicabilità della sopra citata teoria, vogliamo considerare due esempi semplici che riguardano la teoria delle equazioni differenziali ordinarie e la teoria della probabilità.
Esempio 1. - Sia dato un sistema di d'Alembert, cioè un sistema lineare e omogeneo,
con matrice A di elementi αij costanti. Supponiamo che il polinomio minimo di A possieda solo fattori lineari; questo caso si ha in particolare se A è hermitiana (per esempio reale e simmetrica) o più in generale normale. Sia inoltre S un operatore lineare di Cn, che trasforma la base canonica nella base corrispondente alla forma di Jordan; allora la matrice
è diagonale, e i λν (ν = 1, ..., n) sono gli autovalori (su R o su C) di A. Si scriva la (9) nella forma x• = Ax e si ponga z = Sx, allora segue da (d/dt) (Sx) = x• = z• = (SAS-1)Sx = Jz, che il sistema (9) prende la forma z• = Jz o z•i = λizi essendo zi le componenti di z. Questa ha la semplice soluzione zi = ci exp (λit), (i = l, ..., n), dove le ci indicano delle costanti scelte arbitrariamente. Poiché x = S-1z, quando venga posto S-1 = (βij), la soluzione generale della (9) è della forma
Ogni scelta del ‛vettore costante' (c1, ..., cn) dà luogo a una soluzione x = (xi) della (9). Scegliendo n vettori (c1, ..., cn) linearmente indipendenti e considerando la relativa e adeguata soluzione x (t) della (9), ogni soluzione può essere ottenuta come combinazione lineare di queste.
Esempio 2. - Consideriamo un sistema aleatorio (ad esempio una pallina sul piatto di una roulette) che può trovarsi in n (∈ N) diverse condizioni. Per un esperimento ripetibile, sia pij (i, j = 1, ..., n) la probabilità che con questo esperimento il sistema passi dalla condizione i alla condizione j.
Poiché è pij ≥ 0 e
l'annessa matrice P = (pi j) (operatore su Cn) si dice ‛stocastica'. Le sue potenze Pk = (p(ikj)) sono parimenti stocastiche; i loro elementi descrivono la probabilità di transizione da i → j dopo k realizzazioni dell'esperimento. I vettori positivi x = (xi) (xi ≥ 0, i = 1, ..., n) con
xi = 1 si interpretano come distribuzioni (di probabilità). Le matrici stocastiche sono sempre ergodiche in media (v. cap. 2, § a):
La matrice Q è ancora stocastica; per una data distribuzione iniziale x0, Pk x0 (k → ∞) tende ‛in media' verso z = Qx0; z è un vettore fisso di P, cioè una distribuzione che non cambia con la ripetizione dell'esperimento con probabilità 1. Questo segue subito dall'ultimo teorema del cap. 2, § c. Vogliamo infine menzionare un caso speciale. Se pij > 0 per tutti gli i, j = 1, ..., n, è facile provare che P possiede sul cerchio spettrale ∣λ∣ = 1 solo l'autovalore 1. L'ultima osservazione riportata nel cap. 2, § c, dice che Pk x0 converge verso y0 (k → ∞); y0 è una distribuzione univocamente determinata (indipendente dalla distribuzione iniziale x0, e lo spazio degli autovettori di P relativo a λ = r (P) = 1 è monodimensionale.
3. Operatori su spazi di Banach
a) Operatori lineari limitati
Sia (come nel cap. 2, § a) E uno spazio vettoriale su K = R o K = C. Si dice che E è ‛normato' quando è data una funzione x → ∣x∣ di E su R che soddisfi gli assiomi
se lo spazio E è completo nella metrica d (x, y) = ∥x - y∥ (cioè ogni serie di Cauchy converge), E si dice uno ‛spazio di Banach'. Ad esempio, C (L) - lo spazio di tutte le funzioni continue su L compatto a valori su K con norma ∥f∥ = sup {∣ (f (t)∣ : t ∈ L)} - è uno spazio normato; e se (X, Σ, μ) è uno spazio di misura, lo spazio lineare di tutte le (ovvero, classi di equivalenza di) funzioni X → K p-integrabili (1 ≤ p 〈 + ∞), con la norma
diventa uno spazio di Banach, che sarà indicato con Lp (μ).
Un sottoinsieme B ⊂ E si dice ‛limitato', nel caso in cui è sup {∥x∥: x ∈ B} 〈 + ∞. Siano E, F normati e T: E → F un operatore (lineare) che porta i sottoinsiemi limitati di E in sottoinsiemi limitati di F di modo che ∥T∥ - : = sup {∥Tx∥ : ∥x∥ ≤ 1} definirà una norma sullo spazio L (E, F) di tutti gli operatori limitati (‛norma dell'operatore'); oltre a F, anche L (E, F) è uno spazio di Banach. Per F = K (valore assoluto come norma) si pone L (E, F) = E′, e E′ viene chiamato lo ‛spazio duale' di E. Nel seguito ci occuperemo in prevalenza del caso E = F, K = C. Lo spazio degli operatori L (E) = L (E, E), se si indica con ST la composizione (moltiplicazione degli operatori), soddisfa anche le relazioni ∥ST∥ ≤ ∥S∥ ∥T∥, ∥I∥ = 1, dove I : E → E indica l'applicazione identità (operatore unità). Notiamo inoltre che se E, F sono di dimensione finita, ogni operatore T : E → F è limitato e L (E, F) è sempre uno spazio di Banach.
b) Spettro e calcolo funzionale
Sia ora E ≠ {0} uno spazio di Banach complesso (K = C) e T ∈ L (E); per λ ∈ C si scriverà λ - T = λI - T. Come ‛spettro' σ (T) di T si indica l'insieme di tutti i λ ∈ C per i quali λ - T non possiede l'inversa in L (E); ρ (T) = Cσ (T) si dice ‛insieme risolvente' di T. Vale la seguente proposizione fondamentale: lo spettro σ (T) è un sottoinsieme compatto, non vuoto, di C; per ∣λ∣ > lim ∥Tn∥1/n vale sempre λ ∈ ρ (T). Il limite di tale teorema esiste sempre e sarà indicato come ‛raggio spettrale' r (T) di T (si confronti con quanto detto nel cap. 2: per dim E 〈 + ∞, r (T) è uguale al massimo dell'insieme degli autovalori di T). Per ∣λ∣ > r(T) il ‛risolvente' R (λ, T) = (λ - T)-1 sarà dato dalla (serie di Neumann):
Il risolvente λ → R (λ, T) è una funzione localmente olomorfa su ρ (T) a valori in L (E) (nell'ipotesi che sia σ (T) ≠ ∅).
Poiché L (E) è un'algebra (complessa), è possibile, come nel caso di dimensione finita, per ogni polinomio complesso p(z) =
definire l'operatore
Inoltre è facile riconoscere che l'applicazione p → p (T) è un omomorfismo dell'algebra polinomiale nell'algebra L (E). Diversamente dal caso di dimensione finita, esiste qui un T che annulla il polinomio soltanto quando lo spettro σ (T) è finito e consiste solo di poli del risolvente. L'omomorfismo dato dalla (10) si può estendere su una classe essenzialmente più grande di funzioni. Consideriamo (al solito T ∈ L (E), E ≠ {0}) la classe F (T) di tutte le funzioni localmente olomorfe su σ (T), f : D ( f ) → C; due tali funzioni f, g saranno considerate come equivalenti quando c'è un insieme aperto contenuto in D (f) ⋂ D (g) e che contiene σ (T), nel quale f e g coincidono. L'‛algebra quoziente' (dopo questa relazione di equivalenza) è ancora indicata con F (T). Un teorema dovuto a Gel′fand afferma che l'applicazione p → p (T) data dalla (10) sarà estesa con la formula
a un omomorfismo F (T) → L (E). Per la precisione, si considerano in F (T) funzioni (non necessariamente continue), il cui campo di definizione D (f) comprende un insieme aperto U (f) con frontiera Γ ( f ); Γ ( f ) deve in questo caso essere costituita da un numero finito di curve di Jordan rettificabili, orientate in senso positivo al modo usuale. Inoltre, ogni punto di σ (T) deve giacere esattamente all'interno di una di queste curve.
Vogliamo mostrare con un esempio che l'omomorfismo (10) giunge sicuramente fuori dell'algebra polinomiale, nel caso in cui σ (T) non sia connesso. Siano σ, σ′ sottoinsiemi chiusi e complementari di σ (T), entrambi non vuoti. Sia inoltre f una funzione localmente olomorfa su σ (T) = σ ⋃ σ′ con f (z) = 0 (z ∈ σ′), f (z) = 1 (z ∈ σ) e Γ ( f ) = C1 ⋃ C2. Poiché f2 = f, f (T) = P è una proiezione, la scomposizione E = P (E) + (I-P)E riduce T e risulta σ (T ∣PE) = σ, σ (T∣(I-P)E) = σ′. In particolare: se λ0 è un punto isolato di σ (T), σ = {λ0}, lo spettro di T∣PE è costituito dall'unico punto λ0.
Sia E uno spazio di Banach, E′ il suo spazio duale; allora, relativamente alla forma bilineare 〈 ϕ, x> = ϕ (x) (x ∈ E, ϕ ∈ E′) la coppia E, E′ è detta ‛sistema duale (canonico)'. Come nel caso di dimensione finita, con l'identità 〈 ϕ, Tx> = 〈T′ ϕ, x> viene definito un operatore T ′ ∈ L (E′), che viene indicato come operatore ‛trasposto'. Per questo operatore T′ vale: σ (T′) = σ (T) (ne consegue r (T′) = r (T)), così come ρ (T′) = ρ (T) e F (T′) = F (T). La formula dell'omomorfismo (11) vale analogamente con R (λ, T′) = R (λ, T)′ per tutti i λ ∈ ρ (T).
c) Operatori compatti
Al contrario di quanto si otteneva nel cap. 2, un operatore limitato su uno spazio di Banach di infinite dimensioni in generale non possiede alcun autovalore. Si consideri, ad esempio, lo spazio E = C [0, 1] e l'operatore T dato dalla Tf (t) = ∫0t f (s)ds. Nelle loro proprietà spettrali gli operatori compatti sono però molto simili alle matrici finite del cap. 2; qui si dice che T ∈ L (E) è ‛compatto' quando, per ogni B ⊂ E limitato, l'immagine T (B) è relativamente compatta. Menzioniamo, in primo luogo, la seguente importante proposizione: sia T ∈ L (E) compatto. Lo spettro σ (T) è finito o numerabile; in quest'ultimo caso si ha solo 0 come punto di accumulazione. Ogni 0 ≠ λ ∈ σ (T) è un autovalore e lo spazio di tutti gli autovettori corrispondenti a λ (autospazio di λ) è di dimensione finita. L'operatore nominato all'inizio T : f → ∫0t f (s)ds (detto ‛di Volterra') non ha autovalori sebbene sia compatto; si ha r (T) = 0. La teoria degli operatori compatti, che peraltro risale a D. Hilbert e soprattutto a F. Riesz, ha le sue origini nella teoria delle equazioni integrali di Fredholm; queste ultime, d'altra parte, hanno come esempio preminente le equazioni che intervengono nel classico problema delle condizioni al contorno della teoria del potenziale (v. equazioni funzionali, vol. II).
Per gli operatori compatti vale ancora, nella teoria delle equazioni integrali, la seguente importante affermazione: sia λ ≠ 0, T compatto. Allora le equazioni λx - Tx = y (x, y ∈ E) e λx′ - T ′x′ = y′ (x′, y′ ∈ E′) sono entrambe, per tutti gli y, y′ rispettivamente su E e su E′, univocamente risolubili, o entrambe le equazioni omogenee (y = 0, y′ = 0) hanno le stesse soluzioni non nulle linearmente indipendenti. Nell'ultimo caso le equazioni non omogenee sono risolubili solo per gli y ∈ E e rispettivamente y′ ∈ E′, che annullano il nucleo di λ - T′ e rispettivamente di λ - T. Questa è la famosa ‛alternativa di Fredholm' (sugli operatori compatti v. Dunford e Schwartz, 1958-1971; v. anche analisi, vol. I).
d) Operatori hermitiani, normali e unitari
Il prodotto interno (x, y) → (x∣y) per spazi di dimensione finita è stato introdotto nel cap. 2, § b; la definizione, per analogia, è applicabile su qualsivoglia spazio vettoriale su C. Se per esempio H = L2(μ), (f ∣ g) = ∫ −fgdμ è un prodotto interno (prodotto scalare) su H, e ∥ f ∥ = (f ∣ f)1/2 definisce una norma su H. Uno spazio vettoriale H su C così normato si dice ‛spazio di Hilbert' quando (H, ∥•∥) è completo (ossia è uno spazio di Banach). Si può mostrare che ‛ogni' spazio di Hilbert H è isometricamente isomorfo a uno spazio L2(μ) per una scelta opportuna di (X, Σ, μ). Per la misura numerica su N (con μ ({n}) = 1, n ∈ N) si ottiene lo spazio delle serie l2 di tutte le serie x = (xn) a quadrato sommabile; il prodotto interno è dato da
Sia d'ora in poi H uno spazio di Hilbert (su C) e sia T ∈ L (H). Come nel cap. 2, § c, l'‛operatore aggiunto' T* di T definisce l'identità (Tx∣ y) = (x∣T*y) (x, y ∈ H ); valgono inoltre le regole (T + S)* = T* + S*, (αT)* = ᾱT*, (ST)* = T*S* e T** = T, così come σ (T*) = −σ− (−T−). Un operatore A ∈ L (H) si dice ‛hermitiano', nel caso in cui risulti A = A*. Una teoria completamente analoga a quella descritta nel cap. 2, § c, si può costruire per gli operatori hermitiani compatti; in particolare vale il teorema degli assi principali con l'eccezione che il numero degli autovalori potrebbe essere infinito. In particolare vale (corrispondentemente alla 8)
in cui Pn è sempre una proiezione ortogonale con uno spazio immagine Pn (H) di dimensione finita; P0 è la proiezione ortogonale dello spazio nullo (nucleo) di A.
Per gli operatori non compatti (hermitiani) A, la (12), secondo Dunford e Schwartz (v., 1958-1971), deve essere sostituita con la rappresentazione più generale
in cui la distribuzione spettrale λ → P (λ) soddisfa le seguenti condizioni: sia a = inf σ (A), b = sup σ (A) e qualsivoglia x ∈ H; sia λ ∈ [a, b]. Allora λ1 ≤ λ2 implica (P (λ1)x∣x) ≤ (P(λ2)x∣x); λ → (P (λ) x∣x) è continua a sinistra su [a, b) ⊂ R; e P (a) = 0, P (b) = I. Sotto queste condizioni, la distribuzione spettrale λ → P (λ) è univocamente determinata; la (13) contiene il ‛teorema spettrale' per gli operatori hermitiani. Per gli operatori non compatti non c'è bisogno di dare gli autovalori. Ad esempio, sia (Af ) (t) = tf (t), f ∈ H = L2 (μ) (μ è la misura di Lebesgue su [0, 1]); λ0 ∈ σ (A) è un autovalore quando λ → (P (λ)x∣x), per almeno un x ∈ H, ha, in corrispondenza a λ0, un salto.
Come nel caso dim H 〈 ∞, è possibile scomporre ogni T ∈ L (H), con A = (1/2) (T + T*), B = (1/2 i) (T - T*), in componenti hermitiani: T = A + iB. AB = BA è equivalente a TT* = T*T e in questo caso T si dice ‛normale'. Se A e B hanno rispettivamente le distribuzioni spettrali P1 e P2, P1 e P2 commutano e T ha la rappresentazione spettrale seguente:
Infine, si dice che U ∈ ℒ(H) è ‛unitario', quando UU* = U*U = I. Allora l'operatore T ∈ ℒ (H) è unitario quando è normale e σ (T) è contenuto nel cerchio unitario complesso ∣z∣ = 1. Gli operatori unitari di H costituiscono un gruppo, detto il gruppo delle isometrie di H. La teoria delle rappresentazioni dei gruppi astratti, un campo vasto e importante, si occupa di omomorfismi di dati gruppi in un gruppo di operatori unitari di un appropriato spazio di Hilbert H.
Per gli operatori normali A ∈ ℒ (H), si può estendere il calcolo degli operatori (v. 11; v. cap. 3, § b), in virtù della (14), sull'algebra di tutte le funzioni di Borel limitate su σ (A):
In particolare f → f (A) definisce un isomorfismo di algebre che conserva la norma dalle funzioni continue f: σ (A) → C sulla sottoalgebra di L (H) generata da A, A* e I , e chiusa nella norma dell'operatore. Quindi, ad esempio, la radice quadrata di un operatore autoaggiunto, il cui spettro non è negativo, è univocamente definita.
Una rilevante classe di operatori su uno spazio di Hilbert - importante, fra l'altro, nella meccanica statistica quantistica dei sistemi a molte particelle - è quella formata dagli operatori con traccia. Un operatore T si dice ‛con traccia' quando esistono due sistemi ortonormali numerabili (en)n ∈ N e (fn)n ∈ N in H e una serie di numeri complessi (αn) tale che
e
per ogni x ∈ H. Gli operatori con traccia sono notoriamente compatti, in quanto sono limite di operatori con una immagine di dimensione finita. Pertanto, un operatore autoaggiunto S è con traccia esattamente quando esiste una rappresentazione della suddetta forma con fn = en, e quindi gli αn sono gli autovalori di S. Osserviamo infine che rispetto a una base ortonormale (v. cap. 2, § c), cioè un sistema ortonormale massimale, si può rappresentare ogni operatore su H con una matrice; tuttavia, le analogie con il cap. 2, § c, sono in generale molto limitate e non è pertanto possibile spingere ulteriormente il discorso in questa direzione.
e) Operatori positivi su reticoli di Banach
Gli spazi di Banach Lp (μ) (1 ≤ p ≤∞) hanno, come molti spazi di funzioni, una struttura di ordine ( f ≤ g significa f (t) ≤ g (t) quasi ovunque rispetto a μ), mediante la quale diventano ‛reticoli vettoriali' (‛spazi di Riesz'). Se inoltre un tale spazio E è uno spazio di Banach e la norma è legata all'operazione di reticolo f → ∣f∣ con ∣f∣ ≤ ∣g∣ ⇒ ∥f∥ ≤ ∥g∥, si può parlare di un reticolo di Banach (v. Schaefer, 1974). In completa analogia con il cap. 2, § d, si dice che un operatore A ∈ L (E) è ‛positivo' (in simboli A ≥ 0) nel caso in cui per 0 ≤ f ∈ E segue sempre Af ≥ 0. Gli operatori positivi su reticoli di Banach hanno una voluminosa teoria con significative applicazioni alle equazioni di evoluzione, come ad esempio l'equazione di trasmissione del calore
,
e alla teoria strettamente collegata dei semigruppi a un parametro (v. cap. 4, § d). Come esempio prendiamo il seguente teorema, che generalizza quello citato nel cap. 2, § c: sia E un reticolo di Banach e 0 ≤ A ∈ L (E). Vale sempre r (A) ∈ σ (A). Inoltre, r (A) = ∥A∥ e r (A) ε ∈ σ (A) per ∣ε∣ = 1, e così vale anche r (A) εk ∈ σ(A) per tutti gli interi k. Anche lo spettro periferico {λ ∈ σ (A): ∣λ∣ = r(A)} nel caso r (A) = 1 è un'unione finita di gruppi di radici unitarie o l'intero cerchio unitario.
4. Operatori illimitati
a) Introduzione
Nella maggior parte dei problemi che sorgono nelle applicazioni alle scienze naturali si arriva a equazioni alle derivate parziali, quali:
Queste equazioni erano il punto di arrivo per interi settori dell'analisi moderna, come ad esempio la teoria delle equazioni di evoluzione o la teoria dei sistemi complessi della meccanica quantistica con forze di scambio. Una caratteristica di queste teorie è che il comportamento degli operatori
,
come quello di
è lineare, ma non sono definiti sugli spazi usuali di funzioni C (K) o Lp (Ω, Σ, μ), né, relativamente alle norme usuali, sono limitati (v. cap. 3). Per lo più appartengono alla classe degli ‛operatori illimitati' sugli spazi di Banach E, ossia sono applicazioni lineari A di sottospazi lineari D(A) → E, non continue e i cui campi di definizione D(A) sono compatti in norma in E, vale a dire ogni punto di E è il valore limite di una serie convergente in norma su D(A). Un tale operatore A si dice ‛chiuso' quando il suo grafico G (A) : = {(x, Ax): x in D(A)} è chiuso nel prodotto E × E. Dato che gli operatori che derivano dalle applicazioni raramente sono chiusi, da qui in avanti si considererà la classe più grande degli operatori chiudibili: A si dice ‛chiudibile' quando la chiusura −G− (−A−) è ancora il grafico di un'applicazione, che è detta ‛chiusura' À di A. Per le discussioni teoriche ci si riferisce ugualmente alla chiusura Ā del dato operatore A.
b) Spettro
Come nel caso limitato, anche per quello illimitato è possibile definire lo ‛spettro' dell'operatore chiuso A; σ (A): = {λ in C: (λI - A) non è biettivo da D su E}. Il suo complemento Cσ (A) si chiama ancora ‛insieme risolvente' ρ (A). Contrariamente al caso di un operatore limitato, lo spettro può essere vuoto o coincidere con tutto C. Sia ρ (A) non vuoto: allora è possibile definire, come nel caso limitato, il ‛risolvente' R (., A) come funzione di ρ(A) su L (E). R (., A): λ → R (λ, A): = (λI - A)-1. Così come A, anche (λI - A) e R (λ, A) sono chiusi e definiti su tutto E, e anche continui (secondo il teorema di Banach sui grafici chiusi) e R (., A) è una funzione olomorfa. In base a quanto detto nel cap. 2, in linea di principio si può arrivare a determinare lo spettro di R (λ, A) e perciò anche lo spettro di A, poiché per un fissato μ in ρ (A) si ha che l'applicazione λ → (μ - λ)-1 è biettiva di ρ (A) su ρ (R (μ, A)) {0}. Quindi ρ (A) è aperto.
Queste riflessioni sono particolarmente interessanti quando R(μ, A) ha proprietà supplementari, per esempio se è compatto. Un tipico esempio di operatore illimitato con un risolvente compatto proviene dai cosiddetti problemi regolari con valori assegnati al contorno per le equazioni differenziali ordinarie e, rispettivamente, per le equazioni differenziali ellittiche con la condizione di Dirichlet in una regione limitata di Rn o su una varietà compatta. Un altro esempio è costituito dall'operatore energia degli oscillatori armonici nella meccanica quantistica. Gli autospazi del risolvente R (μ, A) per autovalori non nulli sono naturalmente autospazi di A stesso e secondo quanto detto in precedenza (v. cap. 3, § c) di dimensione finita.
c) Operatori speciali
Consideriamo in primo luogo gli operatori simmetrici e hermitiani negli spazi di Hilbert. Sia H uno spazio di Hilbert su C, con prodotto scalare (x, y) → (x∣y). Un operatore compatto A si dice ‛simmetrico' quando per ogni x, y nel campo di definizione D(A) vale sempre (Ax∣y) = (x∣Ay). Operatori simmetrici provengono ad esempio da operatori differenziali con adatte condizioni al contorno. Un operatore simmetrico A con ± i in ρ (A) si dice, in accordo con il caso degli operatori limitati, ‛hermitiano' o ‛autoaggiunto'. Gli operatori autoaggiunti rappresentano del resto le osservabili nella formulazione assiomatica della meccanica quantistica. Per tali operatori, la ‛trasformata di Cayley' (A - i) (A + i)-1 unitaria è alla base delle proprietà di simmetria e il teorema sulla scomposizione spettrale degli operatori unitari (v. cap. 3, § d; v. 13) fornisce il corrispondente teorema sugli operatori autoaggiunti (v. Dunford e Schwartz, 1958-1971): sia A un operatore autoaggiunto con un campo di definizione D(A) in uno spazio di Hilbert H. Allora vi è una distribuzione spettrale λ → P (λ) definita in generale su tutto R, tale che per ogni y in D(A) valga sempre Ay = ∫+_$%$∞∞ λdP (λ)y. Per qualsivoglia insieme chiuso B ⊂ R, gli spazi proiezione P (B) (H): = {∫B dP (λ)x: x in H} = : HB sono invarianti rispetto a R(λ, A) (λ in ρ(A)). Se B è compatto, HB è contenuto in D(A), è invariante rispetto a A e A è limitato su HB con la norma ∥A∣HB∥ ≤ max {∣λ∣: λ in B}. Infine si ha σ (A∣HB) = σ (A) ⋂ B.
In generale, un problema estremamente difficile è quello dell'estensione degli operatori simmetrici agli operatori autoaggiunti, in primo luogo perché i dati provenienti dalle relative applicazioni implicano per gli operatori solo la proprietà di simmetria. Un operatore simmetrico A può essere esteso a un operatore autoaggiunto quando le dimensioni dei complementi ortogonali delle immagini di (A + iI) e (A - iI), i cosiddetti ‛indici di difetto', concordano. Questo è ad esempio il caso quando l'insieme dei valori numerici dell'applicazione W (A) = {(x∣Ax) : ∥x∥ = 1, x in D(A)} è inferiormente (o superiormente) limitato, condizione che spesso può essere motivata nelle applicazioni. L'operatore simmetrico A possiede un'estensione univoca a un operatore autoaggiunto continuo quando l'immagine (A ± iI) (H) è compatta, vale a dire quando entrambi gli indici di difetto sono nulli.
Per la teoria delle equazioni differenziali astratte sono importanti certi operatori chiusi e illimitati su spazi di Hilbert, i cosiddetti operatori ‛dissipativi'. Essi soddisfano la disuguaglianza della ‛parte reale' ((x∣Ax) ≤ 0 (x in D (A)). Un tale operatore si dice ‛massimamente dissipativo' quando il suo insieme risolvente contiene un numero positivo; allora esso riveste l'asse reale positivo, e il risolvente R (λ, A) soddisfa per tale valore la disuguaglianza ∥R (λ, A)∥ ≤ 1/λ.
Inoltre, quando ad esempio lo spazio di Banach E è uguale a C (K) (v. cap. 3, § a) o più in generale a un'algebra di operatori (v. cap. 5), le derivazioni illimitate svolgono un ruolo importante per l'evoluzione temporale dei sistemi fisici (sia classici che quantistici): si dice che un operatore A è una ‛derivazione' quando il suo campo di definizione è una sottoalgebra e soddisfa sempre la regola del prodotto di Leibniz A(x y) = A(x)y + xA(y). Infine, sia A un operatore lineare definito su un sottospazio compatto D(A) di uno spazio di Banach E. Nello spazio duale E′ di E (v. cap. 3, § c) sarà definito un operatore lineare A′, ponendo 〈 ϕ, Ax> = 〈A′ ϕ, x> per tutti gli x in D(A), il cui dominio è il sottospazio D(A′) di tutti quei ϕ in E′, per cui l'applicazione x in D(A) → 〈 ϕ, Ax> è continua. Se ρ (A) non è vuoto, allora D (A′) è compatto in E′ per la topologia data dalla seminorma px: ϕ → ∣〈 ϕ, x>∣, la cosiddetta ‛topologia w*'. Come nel caso limitato, chiameremo A′ ‛trasposto' di A. In generale D(A′) non è compatto in norma in E′, così che A′ è considerato solo in un senso più generale come un operatore illimitato. Si può porre in questo caso semplicemente σ (A′): = σ (A).
d) Semigruppi a un parametro e il problema astratto di Cauchy
Le equazioni differenziali del calore e di Schrödinger (v. cap. 4, § a) possono essere scritte nella forma astratta, x• (t) = Ax (t), x (0) = x0, dove A è un operatore illimitato in un appropriato spazio di Banach (per esempio di funzioni) e x0 è un qualsivoglia elemento in D (A). Questo è il cosiddetto ‛problema astratto di Cauchy'. Analogamente al caso di dimensione finita (v., ad es., cap 2, § d, esempio 1), si ottiene - in primo luogo solo formalmente - la soluzione x (t) = exp (At) x0. Per ‛soluzione' del problema astratto di Cauchy, si intende una funzione 0 ≤ t → x (t) continua e differenziabile per t > 0, con x (0) = x0 e x• (t) = Ax (t). Per semplificare il problema si introducono i seguenti concetti. Si considerino le applicazioni t ∈ R+ = s in R: s ≥ 0 → Tt∈ L (E) per le quali valgono le proprietà: 1) per tutti gli x in E è t → Tt (x) continua da R+ in E; 2) Ts+t = TsTt; 3) T0 = I (applicazione identità di E). (Tt) si dice ‛semigruppo a un parametro fortemente continuo'. Corrispondentemente verranno definiti un gruppo a un parametro fortemente continuo e un semigruppo o gruppo a un parametro w*-continuo (sullo spazio duale E′ di E).
Il rapporto fra il problema di Cauchy e i semigruppi a un parametro (e perciò anche i gruppi a un parametro) è chiarito dal teorema di Hille-Yosida (v. Hille e Phillips, 19572): sia (Tt) un semigruppo a un parametro fortemente continuo e D(A) l'insieme di tutti gli x in E per i quali la funzione t → Tt (x) è differenziabile in 0. Allora A: x ∈ D (A) →
Tt (x)∣t=0 =: Ax è un operatore lineare chiuso e compatto con le seguenti proprietà: 1) esiste un ω in R tale che W (ω): = {λ in C: Re (λ) > ω} ⊂ ρ (A); 2) esiste un M > 0 tale che ∣R (λ, A)n∣ ≤ M (Re (λ) - ω)-n per ogni λ in W (ω) e n in N). Inversamente, sia A un operatore chiuso e compatto con le proprietà 1) e 2); allora esiste un semigruppo a un parametro fortemente continuo (Tt), tale che A è la derivata nel valore 0 nel senso sopra descritto. A si dice il ‛generatore' del semigruppo (Tt). Si ha infine il seguente teorema: sia A un operatore chiuso e compatto con insieme risolvente non vuoto. Allora il problema di Cauchy ha per ogni x0 in D(A) una soluzione quando A è un generatore di un semigruppo a un parametro (Tt). Quindi la soluzione è x (t) = Tt (x0). Un teorema completamente analogo può essere provato per i gruppi a un parametro fortemente continui e per i semigruppi a un parametro w*-continui e di conseguenza per i loro generatori.Vediamo adesso alcuni esempi.
Esempio 1. - Sia A in L (E) definito ovunque e limitato. Allora A è il generatore del gruppo Tt = exp (At) = Σ0∞ Tk/k! (la serie converge nella norma dell'operatore). L'applicazione t → Tt è continua nella norma dell'operatore. Reciprocamente, se un semigruppo a un parametro è di questo tipo, il suo generatore è definito ovunque e limitato.
Esempio 2. - Sia A un operatore autoaggiunto con un dominio di definizione D (A) in uno spazio di Hilbert H. Allora iA è il generatore di un gruppo a un parametro fortemente continuo (Ut) di applicazioni unitarie. Le soluzioni del corrispondente problema di Cauchy sono proprio le soluzioni dell'equazione astratta di Schrödinger. Con la distribuzione spettrale P(λ) il gruppo si ottiene come
Da qui segue che gli spazi P (B) (H) (B è un sottoinsieme chiuso di R) sono invarianti rispetto a (Ut).
Esempio 3. - L'operatore compatto A in uno spazio di Hilbert H è massimamente dissipativo precisamente quando è il generatore di un semigruppo a un parametro (Tt) di contrazioni, cioè risulta ∥Tt∥ ≤1 (teorema di Lumer-Phillips; v. Hille e Phillips, 19572).
Esempio 4. - Sia (Ut) un gruppo fortemente continuo di isometrie su uno spazio di Banach E, cioè tale che ∥Ut(x)∥ = ∥x∥. Allora il generatore, contrariamente al caso dei gruppi unitari, non ha più, in generale, la distribuzione spettrale, ma esiste come prima un'applicazione B → E(B) dell'insieme costituito dai sottoinsiemi chiusi di R sull'insieme dei sottospazi chiusi di E per la quale valgono le seguenti proprietà: E(B) è invariante rispetto al gruppo (cioè Ut (E (B)) ⊂ E (B)), e la restrizione A∣E(B)⋂D(A) : = AB è il generatore della restrizione (Ut∣E (B)) del dato gruppo e risulta σ (A) ⋂ B = σ (AB) (teoria spettrale di Arveson).
Esempio 5. - Sia ora E un reticolo di Banach su C. Analogamente al caso di un operatore positivo (v. cap. 3, § e), anche lo spettro periferico del generatore di un semigruppo a un parametro di operatori positivi ha determinate proprietà di simmetria. Si ha infatti il seguente teorema: sia E un reticolo di Banach su C e (Tt) un semigruppo di operatori positivi con generatore A. Allora s (A): = sup{Re (λ): λ in σ (A)} è sempre in σ(A). Se ∥Tt∥ ≤K per ogni t e un K > 0 e inoltre s (A) = 0, allora σ (A) ⋂ iR è costituito da un'unione finita di sottogruppi additivi dell'asse immaginario iR. Qui sup (A) indica il limite superiore del sottoinsieme A di R.
Concludiamo questo paragrafo con alcune considerazioni sul comportamento asintotico. Analogamente al caso di dimensione finita (v. cap. 2, § d), il comportamento delle soluzioni del problema di Cauchy per t → ∞ è strettamente legato allo spettro del generatore A del sopracitato semigruppo (Tt). Sia ω(A): = inft>0 (ln∥(T)∥)/t). Pertanto è sempre ω (A) ≥ s (A). Esiste però, in uno spazio di Banach di dimensione infinita, un esempio (non banale) tale che ω (A) > s (A). Si ha ω (A) 〈 0 quando esiste un τ > 0 tale che ∥Tt∥ ≤ M exp (- tτ) (la cosiddetta stabilità ‛esponenziale uniforme'). Se esiste un K > 0 tale che lim exp (- Kt)Tt (x) = 0 per tutti gli x in D (A), allora il semigruppo (Tt)t≥0 si dice ‛esponenzialmente stabile'. Contrariamente al caso di dimensione finita, esistono semigruppi esponenzialmente stabili ma non con una stabilità esponenziale uniforme. Per semigruppi positivi su reticoli di Banach, la condizione necessaria e sufficiente affinché i semigruppi siano esponenzialmente stabili è s (A) 〈 0. Vi è un nuovo risultato, secondo il quale un semigruppo di operatori positivi su Lp (Ω, Σ, μ) (1 〈 p 〈 ∞) è esponenzialmente stabile quando ha una stabilità esponenziale uniforme. Il significato di questo teorema sta, fra l'altro, nel fatto che moltissimi modelli di termodinamica, di stocastica e di meccanica quantistica (qui, per la verità, solo indirettamente, secondo la cosiddetta ‛formula di Feynman-Katz') conducono a equazioni differenziali astratte ú (t) = Ax (t) nello spazio Lp (Ω, Σ, μ), dove il generatore A è un semigruppo a un parametro fortemente continuo di operatori positivi. La grandezza s (A) può essere inoltre determinata dalla cosiddetta stima a priori.
5. Algebre di operatori
a) Introduzione
Già nei precedenti capitoli è stato fatto uso varie volte, più o meno esplicitamente, del fatto che lo spazio ℒ (H) di tutti gli operatori lineari limitati sullo spazio di Hilbert H costituisce una ‛algebra con involuzione' (T → T*) su ℂ che è completa nella norma dell'operatore. Tanto alcuni problemi fisici - in primo luogo di meccanica quantistica dei sistemi a infiniti gradi di libertà - quanto alcuni problemi di analisi armonica - per esempio della teoria delle rappresentazioni dei gruppi localmente compatti non commutativi - hanno stimolato la ricerca di sottoalgebre di ℒ (H) chiuse in norma e invarianti rispetto all'involuzione T → T*, le cosiddette ‛algebre di operatori'. Queste possono essere caratterizzate facilmente sulla base del teorema di rappresentazione di I. M. Gel′fand, M. A. Neumark e I. Segal per mezzo del seguente, semplice sistema di assiomi per le C*-algebre. Sia A un'algebra su ℂ con un'involuzione (questa è un'applicazione lineare coniugata x → x* di A in se stessa con (xy)* = y*x* e x** = x). Supponiamo inoltre che A sia uno spazio di Banach, la cui norma soddisfa l'equazione ∣x*x∣ = ∣x∣2. Allora A è isomorfa a una sottoalgebra chiusa di ℒ (H) per un appropriato spazio di Hilbert H. Se T è un operatore normale su di uno spazio di Hilbert H, l'algebra di operatori da esso generata è commutativa e, in base al teorema spettrale (v. cap 3, § d), isomorfa all'algebra C (σ (T)) di tutte le funzioni complesse continue sullo spettro σ (T) di T. Più in generale, secondo il teorema di rappresentazione di Gel′fand, ogni algebra commutativa di operatori con l'elemento unità è isomorfa all'algebra C (K) di tutte le funzioni complesse continue di un opportuno spazio compatto K, e inversamente ogni algebra C (K) è isomorfa a un'algebra di operatori su un opportuno spazio di Hilbert. Anche le C*-algebre di dimensione finita sono facilmente caratterizzabili: esse sono somme dirette di algebre del tipo ℒ (Cn) per un opportuno n in N.
b) W*-algebre
Consideriamo che H sia uno spazio di Hilbert con base ortonormale (eα)α∈A, dove A è un qualsivoglia insieme di indici. Sullo spazio T (H) di tutti gli operatori con traccia (v. cap 3, § d) viene definita, per mezzo della ∥T∥1 : = Sp(√T *T) = Σα ((T *T)1/2 eα∣eα), una norma per la quale lo spazio T (H) è completo. Poiché il prodotto di un qualsivoglia operatore limitato per un operatore con traccia è ancora tale, si definisce, per ogni T in T (H), una forma lineare continua ωT su L (H) data da S → Sp (ST). L'applicazione T in T (H) → ωT è un isomorfismo isometrico di L (H) sullo spazio duale T (H)′ di T (H). L'identificazione L (H) = T (H)′ porta con sé la topologia w* data dalla seminorma S → pT (S) : = ∣ωT(S)∣. Sui sottoinsiemi di L (H) di norma limitata essa coincide con la ‛topologia debole dell'operatore' data dalla seminorma S → ∣(Sx∣y)∣ (x, y in H).
Una sottoclasse di algebre di operatori particolarmente importante, sia per le rappresentazioni di gruppi che per i problemi di meccanica statistica quantistica, è la classe delle ‛W*-algebre' (dette anche ‛algebre di von Neumann'), che sono algebre di operatori in L (H) chiuse nella topologia w*. In base alla teoria della dualità, ogni W*-algebra è uno spazio duale W di uno spazio di Banach W* che secondo S. Sakai è univocamente determinato a meno di isometria (il preduale di W). Per questo ogni W*-algebra ha sempre una topologia w* univocamente determinata. Un'applicazione lineare fra due W*-algebre, continua relativamente a queste topologie w*, si dice ‛normale'. Due W*-algebre si dicono ‛isomorfe' quando esiste fra loro un isomorfismo algebrico normale. Particolarmente semplici sono le W*-algebre commutative, che sono isomorfe ad algebre del tipo L∞ (X, Σ, μ) di tutte le classi di equivalenza di funzioni complesse, misurabili, essenzialmente limitate su un adeguato spazio di misura (X, Σ, μ).
Sia A ⊂ L (H). Indichiamo con A* il commutante di A; A*: = {V in L (H) : SV = VS per tutti i V in A}. Se A è invariante rispetto a V → V*, allora A* è una W*-algebra. Il teorema del bicommutante di von Neumann afferma che si possono ottenere in questo modo tutte le W*-algebre: sia A una sottoalgebra di L (H) invariante rispetto all'involuzione. Allora A è una W*-algebra quando A = A**.
Una W*-algebra W con un centro banale (cioè W ⋂ W* = CI) si dice ‛fattore'. Il significato di questo concetto deriva dal fatto che si può rappresentare ogni W*-algebra come integrale diretto di fattori. Qui per integrale diretto non si intende altro che la naturale generalizzazione della somma diretta. Per l'analisi della struttura e della classificazione delle W*-algebre si devono quindi ricercare solo i fattori. I fattori più semplici, nel caso di spazi H di dimensione finita o infinita, sono gli L (H). Una prima classificazione dei fattori, proposta da Murray e von Neumann in una serie di lavori in comune pubblicati tra il 1936 e il 1943, si basa sulla struttura dell'insieme delle proiezioni nell'algebra. Sia W una W*-algebra: due proiezioni ortogonali P, Q in W si dicono ‛equivalenti' (in simboli: P ~ Q) quando c'è un elemento U in W tale che U*U = P e UU* = Q; una proiezione P si dice ‛finita' quando non c'è nessuna proiezione Q equivalente in W tale che sia Q(H) ⊂≠ P(H). Vale il seguente teorema di Murray-von Neumann (v. Connes, 1990): sia W un fattore con spazio preduale separabile W* (cioè W* costituisce un sottoinsieme numerabile e compatto in norma). Allora esiste un'applicazione D dall'insieme delle proiezioni ortogonali di W in −R+ : = {x in R: x ≥ 0} ⋃ {∞} con le seguenti proprietà: a) P ~ Q ⇒ D (P) = D (Q); b) PQ = 0 ⇒ D (P + Q) = D (P) + D (Q); c) inoltre P è certamente finita quando vale D (P) 〈 ∞. Con queste proprietà D è determinata a meno di un fattore λ > 0. Dopo la normalizzazione, per l'insieme dei valori dell'applicazione D, esistono solo i seguenti casi: {1, ..., n} (in questo caso W si dice di tipo In); {1, ..., ∞} (W si dice di tipo I∞); l'intervallo unitario [0, 1] (W si dice di tipo II1); −R+ (W si dice di tipo II∞); infine, {0, ∞} (W si dice di tipo III).
Le algebre di tipo In sono semplicemente L (Cn) e quelle di tipo I∞ sono L (H) con dim H = ∞ . In questi casi D (P) non è altro che la dimensione dell'immagine P (H) di H sotto P. Per il tipo II1 ci si aiuta con un'altra limitazione: una W*-algebra si dice ‛iperfinita' quando esiste una serie crescente di sottoalgebre di dimensione finita, la cui unione è w*-compatta in W. La maggior parte delle W*-algebre che si trovano nelle applicazioni sono iperfinite. Secondo Murray e von Neumann esiste, a meno di un isomorfismo, solo un fattore iperfinito di tipo II1 su uno spazio di Hilbert H separabile, che si ottiene come algebra di von Neumann della cosiddetta rappresentazione regolare destra di un gruppo localmente finito discreto e misurabile, che ha soltanto classi coniugate infinite. Il prodotto tensoriale di questo fattore e di L (H) fornisce un esempio di fattore di tipo II∞. Qui il prodotto tensoriale di due W*-algebre, V ⊂ L (H1) e W ⊂ L (H2) è definito come la W*-sottoalgebra di L (H1 ⊗ H2;) che è generata dagli operatori S ⊗ T con S in V e T in W.
Il passo successivo è stato la classificazione dei fattori di tipo III da parte di A. Connes. Con l'aiuto del prodotto tensoriale infinito L (C2) ⊗ L (C2) ⊗ L (C2) ..., R. Power trovò la cosiddetta algebra dei fermioni, una famiglia (Wλ)0〈λ〈1 di fattori non isomorfi di tipo III che fornì esempi delle classi IIIλ identificate subito dopo da Connes. Esse si ottengono nel modo seguente. Sia ϕ una forma lineare normale su W con ∣ϕ∣ = ϕ (I) = 1 (I: elemento unitario dell'algebra) e ϕ (T*T) ≠ 0 per T ≠ 0 (una tale forma lineare si dice ‛stato fedele e normale' su W). M. Tomita associò a questa un gruppo a un parametro (σtϕ)t∈R w*-continuo di automorfismi di W con ϕ 0 σtϕ = ϕ, il cosiddetto ‛gruppo modulare' di ϕ. Sia Aϕ il suo generatore (v. cap. 4, § d). La classe dei fattori W di tipo III si suddivide ulteriormente mediante lo ‛spettro di Connes' Γ(W) =
σ(Aϕ) (per σ (Aϕ), v. cap. 4, § c). Connes ha potuto dimostrare che questo è sempre uno dei seguenti sottogruppi di R: 1) Γ (W) = {0µ; 2) Γ (W) = {z ln(λ): z in Z}, dove può solo essere 0 〈 λ 〈 1; 3) Γ (W) = R.
Usualmente si associa il valore λ = 0 al caso 1) e il valore λ = 1 al caso 3) in modo da ottenere la suddivisione del tipo III nelle classi IIIλ per 0 ≤ λ ≤ 1. Tutti questi differenti fattori di tipo III si presentano nei problemi della statistica: la sua analisi ha quindi anche grande significato per le applicazioni.
c) Prospettive
Oltre alle W*-algebre, negli ultimi trent'anni hanno svolto un ruolo sempre più importante le C*-algebre. Vi sono diverse linee di sviluppo, fra le quali esistono molteplici relazioni (v. Connes, 1990): l'approccio algebrico in teoria quantistica dei campi (iniziato da D. Kastler, N. Hugenholtz e R. Haag); la cosiddetta deformation quantization (iniziata fra gli altri da E. P. Wigner, J. E. Moyal, F. Berenzin, e sviluppata nella sua forma attuale da M. A. Rieffel), il cui scopo è trovare una formulazione matematica soddisfacente della transizione dalla meccanica quantistica alla meccanica classica (il cosiddetto limite classico ‛ℏ → 0', dove ℏ è il quanto d'azione di Planck); infine, la cosiddetta geometria non commutativa, che si spera riesca a risolvere i problemi sia della geometria differenziale classica che dei differenti rami della meccanica quantistica (v. anche geometria non commutativa, vol. X).
BIBLIOGRAFIA
Connes, A., Géometrie non commutative, Paris 1990.
Dunford, N., Schwartz, J., Linear operators, 3 voll., New York 1958-1971.
Hille, E., Phillips, R. S., Functional analysis and semi-groups, Providence, R. I., 19572.
Kato, T., Perturbation theory for linear operators, Berlin-New York 19762.
Schaefer, H. H., Banach lattices and positive operators, Berlin-New York 1974.