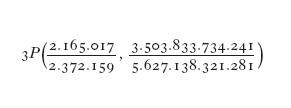Numeri, teoria dei
Numeri, teoria dei
(App. IV, ii, p. 626; V, iii, p. 698; v. aritmetica, IV, p. 370)
La dimostrazione dell'ultimo teorema di Fermat
Le ricerche relative all'ultimo teorema di Fermat, uno dei più famosi e celebrati problemi aperti della matematica degli ultimi tre secoli, hanno determinato progressi fondamentali nelle scienze matematiche e sono state coronate dal successo con la dimostrazione ottenuta nel 1995 dal matematico inglese A. Wiles. L'ultimo teorema di Fermat asserisce che non esistono tre interi positivi x, y e z tali che xn+yn=zn se n è un intero più grande di due. Per n=2 esiste un'infinità di soluzioni che sono note come terne pitagoriche: 3²+4² = 5², 5²+12²=13², 8²+15²=17², ... Tale risultato è associato al nome del giurista e matematico francese P. de Fermat che nel 1637 (o in un anno vicino) scrisse nel margine della sua copia dell'Arithmetica di Diofanto - accanto al problema 8 del Libro 2°, nel quale si chiede di dividere un quadrato nella somma di due quadrati - che "separare un cubo in due cubi, o una quarta (biquadratica) potenza in due quarte potenze, o in effetti una qualsiasi potenza superiore fino all'infinito in due potenze simili è impossibile; ho una dimostrazione meravigliosa di questo fatto. Ma il margine è troppo stretto per contenerla". Alla morte di Fermat, nel 1665, il figlio Samuel raccolse la corrispondenza matematica del padre; questa raccolta fu stampata nel 1670, insieme a una ristampa del Diophantus contenente le note a margine di Fermat. Alla fine del Settecento tutte le altre osservazioni di Fermat erano state trattate in un modo o nell'altro: o erano state dimostrate adeguatamente oppure si era dimostrato che erano false. Solo quest'unica osservazione, da cui il nome di ultimo teorema, era rimasta senza risposta (v. aritmetica: Aritmetica superiore o teoria dei numeri, IV).
Quando Fermat morì, era uno dei più famosi matematici in Europa, sebbene non avesse pubblicato nulla in vita. La sua reputazione proveniva dalla corrispondenza con altri studiosi e da un certo numero di lavori che circolavano sotto forma di manoscritto. È difficile ipotizzare che Fermat abbia scritto una dimostrazione dell'ultimo teorema. In effetti, sembra chiaro che egli stesso non abbia continuato a credere di averne una dopo il momento in cui scarabocchiò l'affermazione nel famoso margine poiché, al di là degli esponenti 3 e 4 (i quali erano alla sua portata e furono menzionati tra i problemi proposti come sfide nelle sue lettere), Fermat non si gloriò mai di questo successo nella sua corrispondenza durante i successivi trent'anni di vita. Oggi Fermat è ricordato principalmente per il suo lavoro in teoria dei n., ma il suo contributo in questo settore era troppo rivoluzionario e avanzato rispetto al suo tempo che non ne comprese completamente l'effettivo valore. Altre parti della sua opera furono più apprezzate dai contemporanei: i contributi all'ottica, particolarmente il principio del tempo minimo e di conseguenza la legge della riflessione e della rifrazione; la geometria analitica (che egli aveva sviluppato indipendentemente da Cartesio) e la teoria delle tangenti, delle quadrature e dei massimi e minimi, vale a dire il suo contributo ai primordi dell'analisi. Questi contributi sono attualmente meno conosciuti, forse perché erano i primi passi in materie che sono ora meglio comprese, mentre il lavoro in teoria dei n., reinterpretato più di un secolo dopo da Eulero e dai successivi fondatori della matematica moderna, risulta attuale e fonte di ispirazione.
Per dimostrare il teorema di Fermat basta provare che nessuna quarta potenza è una somma di due quarte potenze, e - per tutti i primi p dispari - che nessuna potenza p-esima è la somma di due potenze p-esime. Che sia sufficiente considerare questi casi è chiaro, in quanto ogni n. intero n ∙ 2 o è una potenza di 2, e quindi divisibile per 4, oppure è divisibile per qualche primo dispari p; di conseguenza una potenza n-esima (che non sia un quadrato) chiaramente dev'essere anche o una quarta potenza o una potenza p-esima per qualche primo dispari p.
Fermat stesso risolse il caso n = 4 in una delle poche dimostrazioni che ci ha lasciato. Specificatamente, egli mostrò che un triangolo rettangolo con lati interi non può avere per area il quadrato di un intero. Le terne pitagoriche primitive x² + y² = z² sono tutte della forma x = 2uv, y = u² - v², z = u² + v², dove u e v sono interi primi fra di loro non contemporaneamente dispari. Diventa quindi un interessante (e non banale) esercizio notare che la non esistenza del triangolo rettangolo, nelle condizioni di cui sopra, implica che la differenza di due quarte potenze non può nemmeno essere un quadrato, e a maggior ragione una quarta potenza. Un secolo dopo, nel 1753, Eulero ebbe successo con il caso n = 3; nella sua argomentazione si trovava un'evidente lacuna che fu colmata più tardi da C.F. Gauss. Nel 1825 P.G.L. Dirichlet e A.M. Legendre dimostrarono il caso n = 5 e G. Lamé risolse il caso n = 7 nel 1839; Dirichlet aveva dimostrato il caso n = 14 nel 1832.
Per simmetria è spesso conveniente (per es. prendendo c negativo) considerare l'equazione di Fermat nella forma ap+bp+cp=0, dove ovviamente possiamo supporre che a, b, c non abbiano alcun fattore in comune (quindi anche presi a due a due a, b, c non hanno alcun fattore in comune). In quel che segue p sarà un primo dispari. Si vede direttamente che ci sono due casi per le possibili soluzioni: o l'esponente p divide uno fra a, b, c (supporremo sempre che sia c) oppure p non divide nessuno tra a, b, c. In quest'ultima eventualità, nota come il primo caso dell'ultimo teorema di Fermat, è facile mostrare che esiste un intero γ tale che a+b=γp; se invece c è divisibile per p (questo è il secondo caso) allora si ha che a+b=pp⁻¹γp. S. Germain usò queste idee per dimostrare che non esiste alcuna soluzione nel primo caso se si verifica che l'esponente n e il numero kn+1 sono entrambi primi; qui k può assumere diversi piccoli valori. Da questo lavoro, opportunamente generalizzato da Legendre, seguì che l'equazione di Fermat non aveva alcuna soluzione del primo caso per esponenti n più piccoli di 100. Molto più recentemente, L. Adleman e R. Heath-Brown hanno applicato un risultato di E. Fouvry per generalizzare le idee di Germain in modo da dimostrare che il primo caso dell'ultimo teorema di Fermat è valido per un numero infinito di esponenti primi. D'altra parte, N.H. Abel aveva congetturato che nessuno fra x, y, z potesse essere potenza di un primo. Usando delle formule come quelle a cui si è precedentemente accennato si può mostrare che se nell'uguaglianza xn+yn=zn con 0 〈 x 〈 y 〈 z e n ≥ 3, uno fra x, y, z è una qualche potenza qr di un primo q, allora l'esponente n deve essere uguale a un primo p, la potenza del primo deve essere il primo stesso (cioè x=q), z differisce da y di 1 e n divide y(y+1). Tuttavia, fino alla recente dimostrazione di Wiles del teorema di Fermat, in generale non era nemmeno noto se l'equazione di Abel xp+yp=(y+1)p fosse impossibile per interi positivi x e y.
Le formule di cui sopra (formule di Barlow-Abel) sono spesso riscoperte da molte persone, anche da dilettanti che si interessano al teorema di Fermat. In particolare, se le equazioni sono manipolate nella loro forma non simmetrica è molto facile commettere un piccolo errore e quindi ottenere una contraddizione spuria la quale 'dimostra' che in effetti l'equazione di Fermat non ha soluzioni intere. È impressionante contemplare il numero quasi incalcolabile di ore trascorso dagli 'scopritori' nel percorrere tali strade senza uscita; molto tempo è stato impiegato nel trovare tali errori e nello spiegare ai riluttanti 'dimostratori' che il loro approccio è sempre senza speranza. Sfortunatamente, l'argomentazione di Wiles, argomentazione coronata da successo, non ha ancora dissuaso definitivamente dal tentativo di scoprire una 'argomentazione elementare', che non si avvalga cioè di risultati matematici di un certo spessore. Bisogna però ricordare che negli anni Settanta G. Terjanian fece notare, usando solo questi metodi elementari, che se x²p+y²p=z²p ha una soluzione intera allora 2p divide x o y.
Gli sviluppi del lavoro di E. Kummer
L'ultimo teorema di Fermat riguarda soluzioni razionali intere di un'equazione. Eppure sembra che si possa semplificare lo studio dell'equazione di Fermat introducendo degli interi generalizzati, i cosiddetti interi ciclotomici, che implicano le radici p-esime dell'unità. L'idea è quella di vedere l'equazione xp+yp=zp nella forma Πp⁻¹r=₀(x+πrpy)=zp, dove πp è una radice primitiva p-esima dell'unità. Si potrebbe dunque essere tentati di provare che ogni fattore lineare (x+πrpy) sia essenzialmente una potenza p-esima, come succede nel caso in cui si ha a che fare con interi razionali. Tuttavia Kummer vide che, in generale, non esiste alcuna fattorizzazione unica nei domini degli interi ciclotomici e, ancora peggio, non esistono unità non banali; egli affrontò queste difficoltà introducendo la nozione di n. ideale (v. aritmetica: La teoria dei numeri in un corpo algebrico, IV). Con tale mezzo si vede che tutti gli ideali principali (x+πrpy) sono potenze p-esime di ideali del p-esimo campo ciclotomico, e più precisamente potenze p-esime di ideali principali se il n. di classe di quel campo è primo con p. I primi p con la suddetta proprietà sono detti regolari. Kummer dimostrò l'ultimo teorema di Fermat per tale classe di primi nel 1847. Le sue ricerche procurarono una caratterizzazione apparentemente diretta della regolarità in termini del comportamento dei n. di Bernoulli modulo p e il suo studio dei campi di n. ciclotomici diede inizio alla branca ora nota come teoria algebrica dei numeri. Infine - trattando i primi 37, 59 e 67, i quali sono solo 'un po' irregolari' - Kummer dimostrò l'ultimo teorema di Fermat al di là del numero 100 (fino a 167, dove i calcoli divennero troppo gravosi). Nel 1856 l'Académie des sciences di Parigi, che sei anni prima aveva offerto una medaglia d'oro e un premio di 3000 franchi al matematico che avesse risolto il problema di Fermat, attribuì la medaglia a Kummer "per le sue bellissime ricerche sui numeri complessi composti da radici dell'unità e da interi" e decise di ritirare la questione dalla competizione. Comunque, proprio come Gauss aveva trascurato l'equazione di Fermat considerandola una fra una moltitudine di equazioni diofantee simili, è chiaro che per Kummer l'importanza del suo lavoro sulle leggi di reciprocità superiore andava molto al di là delle sue eventuali applicazioni all'ultimo teorema di Fermat.
Nel 1908 la Königliche Gesellschaft der Wissenschaften di Göttingen aveva annunciato l'istituzione del premio Wolfskehl, fornendo 100.000 marchi "da essere attribuiti alla persona che dimostrerà per prima il grande teorema di Fermat". L'aggettivo 'grande' tende a distinguere il risultato dal 'piccolo teorema di Fermat', secondo cui un primo p divide ap - a per tutti gli interi a (risultato fondamentale per la moderna crittografia a chiave pubblica; v. aritmetica: Numeri primi, IV). Il premio Wolfskehl suscitò grande interesse per il suo valore e un diluvio di dimostrazioni; sebbene sia stato poi grandemente svuotato dall'iperinflazione, senza dubbio ha contribuito notevolmente ad aumentare la notorietà dell'ultimo teorema di Fermat (il premio Wolfskehl, che ammontava alla fine del 20° secolo a 50.000 marchi tedeschi, è stato attribuito nel giugno 1997 a Wiles per la sua dimostrazione). Tuttavia, sorprendentemente, nei 120 anni successivi al monumentale contributo di Kummer, si erano verificati pochi avanzamenti fondamentali lungo quella linea di ricerca. Agli inizi del Novecento il matematico statunitense H.S. Vandiver corresse parte del lavoro di Kummer e raffinò il suo criterio per l'irregolarità. Nel 1993 ulteriori simili raffinamenti e calcoli ingegnosi (fatti anche con l'aiuto del calcolatore) hanno permesso di dimostrare l'ultimo teorema di Fermat per esponenti fino a quattro milioni. Negli ultimi decenni, una serie di lavori basati su una complicata analisi delle condizioni di Kummer ha condotto al criterio di Wieferich relativo al primo caso, secondo cui, se esistesse una soluzione del primo caso per un esponente p, allora p dovrebbe dividere i quozienti di Fermat (ap - a)/p sia per la base a=2 sia per a=3. Ma è stato dimostrato, di nuovo tramite il calcolatore, che i soli primi fino a 10⁹ soddisfacenti il criterio per a=2 sono 1093 e 3511, mentre per la base 3 si ottengono solo 11 e 1.006.002. Nel 1993, A. Granville ha esteso il criterio del primo caso dimostrando che era necessario per tutte le basi fino ad a=89; così si è risolto il primo caso dell'ultimo teorema di Fermat al di là dell'esponente presente in 1014.
D'altra parte, applicando anche tecniche della teoria della trascendenza e delle approssimazioni diofantee, il matematico finlandese K. Inkeri ha mostrato che per un'ipotetica soluzione nel caso dell'esponente p si avrebbe che x, per es., dovrebbe essere maggiore di pp o di espressioni analoghe. Di conseguenza è diventato evidente che non si sarebbe potuto scrivere effettivamente un qualsiasi controesempio all'affermazione di Fermat, perché se ce ne fosse stato uno sarebbe stato composto da interi con milioni di cifre. Inoltre le applicazioni del metodo di A. Baker hanno mostrato che nell'uguaglianza xp+yp=zp (con 0 〈 x 〈 y 〈 z) in ogni caso y - x è approssimativamente grande quanto x; inoltre si ha che z - y è della medesima grandezza oppure z - y=1. Così questi metodi altamente sofisticati non potevano risolvere nemmeno la congettura di Abel.
Altre ricerche hanno riguardato la congettura di Catalan, secondo cui l'equazione xu - yv = 1 ha solo 3² - 2³ = 1 come soluzione intera non banale; tale congettura era considerata più difficile dell'ultimo teorema di Fermat. Eppure, a metà degli anni Settanta, R. Tijdeman raffinò le disuguaglianze di Baker e mostrò che esse implicano che l'equazione di Catalan ha al più un numero finito di soluzioni. Miglioramenti più recenti dei limiti numerici di Baker e applicazioni, fra l'altro, di risultati di Inkeri sulla teoria del campo di classe hanno ridotto notevolmente il dominio in cui possono trovarsi altre soluzioni. Infine, nel 1983 G. Faltings dimostrò la congettura di L.J. Mordell, la quale implica che una curva di genere maggiore di uno ha al più un numero finito di punti razionali (v. numeri, teoria dei, App. V). Questo progresso fondamentale nella geometria aritmetica implica che ogni equazione di Fermat ha al più un numero finito di soluzioni, perché una soluzione intera dell'equazione di Fermat fornisce un punto razionale della curva xp + yp = 1 (qui si è sostituito x/z con x e y/z con y). Per p > 3 tali curve hanno genere maggiore di uno. È semplice mostrare che, come conseguenza, l'ultimo teorema di Fermat vale per quasi tutti gli esponenti n; cioè che la probabilità che un dato esponente fornisca un controesempio è zero.
Nonostante questi importanti risultati, rimanevano ancora molti problemi sulla via aperta da Kummer. In particolare, non si era ancora riusciti a dimostrare l'esistenza di infiniti primi regolari, sebbene si congetturasse con una certa sicurezza che un po' più del 70% dei primi sono regolari, mentre era facile dimostrare che esistono infiniti primi irregolari. Non era ancora noto se il secondo caso dell'ultimo teorema di Fermat fosse valido per un'infinità di esponenti primi. Sembrava che un'idea completamente nuova fosse necessaria. La nuova idea è venuta, come nel caso della dimostrazione di G. Faltings, dall'interazione tra teoria dei n. e geometria algebrica.
La dimostrazione di A.J. Wiles
Allo scopo di chiarire origini e motivazioni del risultato di Wiles è opportuno ricollegarsi a una delle opere più avanzate della matematica greca, l'Arithmetica di Diofanto. In quest'opera Diofanto si occupò principalmente del problema di trovare soluzioni razionali di vari tipi di equazioni con un approccio sostanzialmente geometrico. Nello studio delle terne pitagoriche, egli considera l'equazione x²+y²=1 cercando soluzioni x e y razionali. Dal punto di vista moderno quest'equazione rappresenta una circonferenza e ovviamente (-1,0) è un punto di questo luogo geometrico. Una retta tipica che passa attraverso questo punto è parametrizzata scrivendo x=u - 1, y=tu; questa retta interseca la circonferenza quando u² - 2u+1+t²u²=1 e, se trascuriamo la soluzione u=0, otteniamo u=2/(1+t²); quindi si ha un nuovo punto di intersezione dato da x=(1 - t²)/(1+t²), y=2t/(1+t²). Questa è ovviamente la soluzione menzionata sopra, che mostra ora come la circonferenza possa essere parametrizzata da funzioni razionali. In questo caso otteniamo un numero infinito di soluzioni, date da una formula semplice. Altri problemi possono avere un numero infinito di soluzioni (non date da una formula razionale), solo un numero finito di soluzioni o nessuna soluzione. È opportuno considerare un altro caso.
Il problema 24 del Libro 4° di Diofanto suggerisce di dividere un n. dato in due parti in modo che il loro prodotto sia un cubo meno la sua radice cubica. Per es., se consideriamo il numero 6, si tratta di porre y(6 - y)=x³ - x. Esaminando il problema geometricamente, di nuovo (−1,0) fornisce una soluzione banale, ma se poniamo ora x=u - 1, y=tu otteniamo, dopo la cancellazione della soluzione nota u=0, t(6 - tu)=(u - 1)(u - 2) oppure u² - (3 - t²)u+(2 - 6t)=0. In generale, questo porta a valori irrazionali di u, ma, scegliendo la pendenza della retta (coefficiente angolare) t=1/3 si può ancora cancellare la soluzione nota per ottenere u=26/9: quindi x=17/9, y=26/27 è una nuova soluzione. La cosa importante è che possiamo ora costruire la tangente in questo nuovo punto (soluzione) per trovare un'ulteriore soluzione e così via. In generale, date due soluzioni, la secante produce una terza soluzione. Naturalmente la complessità delle soluzioni minaccia di crescere drammaticamente. Per es., scrivendo nel 1643, Fermat chiede se esistano triangoli rettangoli tali che sia l'ipotenusa sia la somma dei due lati siano dei quadrati. Prendendo i lati come 1/2 (1 ± y) e l'ipotenusa come x², per il teorema di Pitagora abbiamo y²=2x⁴ - 1. Fermat riesce a calcolare la soluzione P(13, 239). Ma il problema geometrico richiede che i lati del triangolo siano n. positivi, così deve essere -1 〈 y 〈 1. La tangente in P fornisce un'ulteriore soluzione
Questo ancora non funziona. Finalmente otteniamo
dalla secante passante per due soluzioni, corrispondenti a un triangolo di lati: a=1.061.652.293.520, b = 4.565.486.027.761, c=4.687.298.610.289.
Non solo questa è una soluzione, ma il metodo garantisce che questa è la soluzione più piccola.
Con equazioni di grado maggiore questo metodo in generale fallisce. Data un'equazione polinomiale a coefficienti interi f(x, y)=0 risulta che ci sono tre casi, apparentemente dipendenti dal grado (totale) di f. E cioè, se f è di grado al più 2, abbiamo infinite soluzioni o nessuna soluzione, e questi casi sono parametrizzati da funzioni razionali: questo è il caso delle curve razionali, curve di genere 0. Se f è di grado 3 abbiamo un numero finito di soluzioni - nel caso che il metodo della 'ascesa infinita' dell'ultimo esempio diventi ciclico - o un numero infinito di soluzioni: questo è il caso delle curve ellittiche, cioè di curve di genere 1. Tali curve naturalmente non hanno niente a che fare con le ellissi (queste ultime sono coniche e possono essere parametrizzate da funzioni razionali), ma ricevono questo nome perché sono parametrizzate dalle cosiddette funzioni ellittiche. In ultimo, abbiamo le curve di tipo generale, di genere g ≥ 2, che sembrano avere solamente punti razionali sporadici, secondo la congettura di Mordell dimostrata da Faltings (v. numeri, teoria dei, App. V). Ricapitolando, il caso interessante - dove non è chiaro se una curva abbia infiniti punti razionali o no - è il caso delle curve ellittiche. In questo senso, paradossalmente, lo studio della collezione delle equazioni comprendenti l'ultimo teorema di Fermat non è di alcun interesse.
La comprensione dell'aritmetica delle curve ellittiche è avanzata notevolmente nella seconda metà del 20° secolo. Una serie di calcoli e l'analogia con risultati noti per i campi di numeri algebrici hanno motivato le notevoli congetture di B.J. Birch e P. Swinnerton-Dyer, e il lavoro di M. Eichler e di G. Shimura ha dato consistenza a un suggerimento di Y. Taniyama secondo il quale le curve ellittiche definite sui razionali sono anche parametrizzate dalle funzioni modulari. Sono stati dimostrati alcuni esempi delle congetture di Birch-Swinnerton-Dyer; il caso più semplice è stato trattato da J.H. Coates e Wiles. Quindi, a metà degli anni Ottanta, si è stabilita una notevole connessione tra questi lavori fondamentali e l'ultimo teorema di Fermat. Il contesto di questa relazione ha avuto origine in parte da uno studio della cosiddetta congettura ABC, secondo la quale un'equazione A+B=C, dove A, B e C sono interi positivi, implica che C non è più grande di una piccola potenza del prodotto dei primi distinti che dividono il prodotto ABC. Si consideri la curva cubica εa,b,c: y²=x(x - a)(x+b), dove a+b=c sono interi distinti. Con questa condizione su a, b e c abbiamo una 'curva di Frey' εa,b,c, una curva ellittica con discriminante essenzialmente abc. Nel 1985 G. Frey fece notare che per uvw∙0 e p > 5, se 2|u e v ≡ 1 mod 4, allora la curva εup,vp,wp è semistabile e la sua presunta esistenza appare, probabilmente, contraddire la congettura di modularità di Taniyama-Shimura per le curve ellittiche sui razionali Q. Nel linguaggio degli anni Settanta, εup,vp,wp non sarebbe potuta essere una curva di Weil. Un suggerimento di J.P. Serre, la sua cosiddetta ε-congettura, fu dimostrato corretto da K. Ribet nel 1986; questi mostrò che in effetti la verità della congettura di modularità, anche semplicemente per il caso delle curve ellittiche semistabili, avrebbe implicato l'ultimo teorema di Fermat. A quel tempo, comunque, si credeva che la congettura di modularità fosse inaccessibile e che la sua dimostrazione fosse distante almeno una generazione.
Ci fu perciò un'enorme sorpresa ed eccitazione quando, nel 1993, Wiles, un matematico britannico che a quel tempo lavorava a Princeton, annunciò (in una conferenza al Newton Institute for Mathematical Sciences dell'università di Cambridge) di aver provato l'ultimo teorema di Fermat tramite la dimostrazione della congettura di modularità per le curve ellittiche semistabili su Q (v. numeri, teoria dei, App. V). A quell'annuncio seguì un periodo di circa un anno, nel quale una sottile lacuna nell'argomentazione fu eliminata. Nel 1995 un articolo di Wiles, insieme a un ulteriore lavoro scritto insieme a R. Taylor, dimostrò finalmente l'asserzione di Fermat. È importante rilevare che l'ultimo teorema di Fermat è stato dimostrato come corollario di risultati estremamente più significativi.
Per capire il valore di questa dimostrazione per la matematica si potrebbe stabilire un confronto ragionevole con il significato che ha avuto lo sbarco sulla Luna per la scienza e la tecnologia. La dimostrazione di Wiles è sensazionale come l'allunaggio e parimenti eccitante per gli spettatori. Di per se stessa la conoscenza del fatto che l'affermazione di Fermat è vera costituisce in realtà un avanzamento poco significativo per la matematica, così come l'effettivo trasporto di persone sulla Luna non ha aggiunto molto alla nostra conoscenza scientifica. L'atterraggio sulla Luna è stato, in effetti, il corollario di un lungo e costante avanzamento scientifico e tecnologico, segnato da alcuni progressi eccezionali; eppure l'allunaggio di per sé non rientra fra essi. Allo stesso modo, l'ultimo teorema di Fermat costituisce il culmine di circa 350 anni di avanzamenti nel campo della matematica. Tuttavia, il lavoro di Wiles rappresenta effettivamente un risultato straordinario, uno fra gli spartiacque fondamentali. Il suo grande contributo è consistito nel mostrare che, in realtà, la congettura di modularità di Taniyama-Shimura-Weil è vera, perlomeno per curve ellittiche semistabili. Questo conferma che l'evidenza 'sperimentale' e contestuale non ha condotto la matematica fuori strada. Si può affermare che il 'Santo Graal' dell'ultimo teorema di Fermat è stato necessario per motivare questo avanzamento.
Per quanto riguarda il futuro si noti che, contemporaneamente all'annuncio di Wiles, H. Darmon e A. Granville hanno dimostrato ciò: il teorema di Faltings implica che l'equazione xr+ys=zt ha al più un numero finito di soluzioni composte da interi primi fra loro x, y, z; questo nel caso in cui 1/r+1/s+1/t 〈 1. Il caso dove la somma dei reciproci degli esponenti è 1 include l'ultimo teorema di Fermat con esponenti 3 e 4 considerando per quest'ultimo esponente il caso (2, 4, 4). F. Beukers ha mostrato che, quando la somma è più grande di 1, esistono infinite soluzioni parametrizzate da un numero finito di insiemi di polinomi in più variabili. Esistono dieci soluzioni note nel primo caso, a cominciare da 3² - 2³=1⁷; la più grande di queste soluzioni è 43⁸+96.222³=30.042.907². In tutte le dieci soluzioni almeno uno degli esponenti è 2. Tenendo presenti questi risultati si può formulare la congettura di Fermat generalizzata, la quale dice che l'equazione di Darmon-Granville non ha alcuna soluzione quando tutti gli esponenti sono maggiori di 2. È sicuramente rischioso suggerire che le dieci soluzioni note siano tutte le soluzioni primitive. Eppure colpisce il fatto che queste soluzioni non contraddicano la congettura di Fermat generalizzata.
Il problema aperto più interessante tuttavia è la congettura ABC. Esiste un numero crescente di indicazioni le quali suggeriscono che tale congettura implichi proprio quei fatti matematici che si sarebbe portati a congetturare su basi più affidabili. Inoltre si può dimostrare una congettura analoga nella teoria dei campi di funzioni. Sebbene queste argomentazioni non siano trasferibili al caso aritmetico, esse si sono dimostrate estremamente affidabili nel suggerire dove si trova la verità anche in teoria dei numeri.
bibliografia
H.M. Edwards, Fermat's last theorem. A genetic introduction to algebraic number theory, Berlin 1977.
P. Ribenboim, 13 Lectures on Fermat's last theorem, Berlin 1979.
G. Shimura, Yutaka Taniyama and his time: very personal recollections from Shimura, in Bulletin of the London mathematical society, 1989, 21, pp. 186-96.
E.T. Bell, The last theorem, Washington 1990.
K. Ribet, From the Taniyama-Shimura conjecture to Fermat's theorem, in Annales de la Faculté des sciences de l'Université de Toulose, 1990, 11, 1.
R. Taylor, A. Wiles, Ring-theoretic properties of certain Hecke algebras, in Annals of mathematics, 1995, 141, pp. 553-72.
A. Wiles, Modular elliptic curves and Fermat's last theorem, in Annals of mathematics, 1995, 141, pp. 443-551.
A. van der Poorten, Notes on Fermat's last theorem, New York 1996.
Modular forms and Fermat's last theorem, ed. G. Cornell, J.H. Silverman, G. Stevens, New York 1997.
S. Singh, Fermat's enigma: the epic quest to solve the world greatest mathematical problem, New York 1997 (trad. it. L'ultimo teorema di Fermat, Milano 1997).