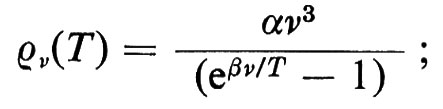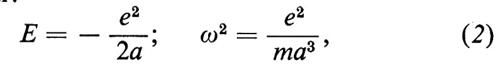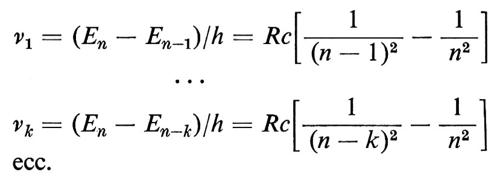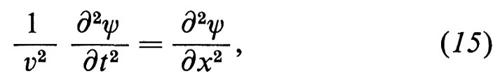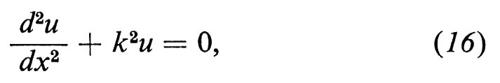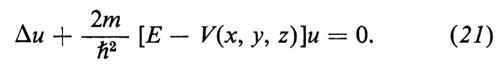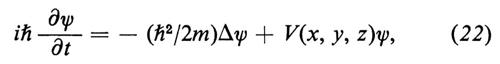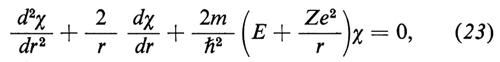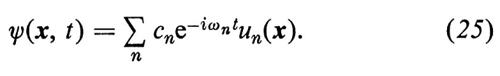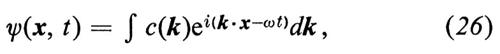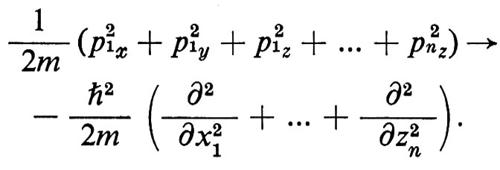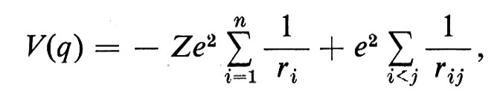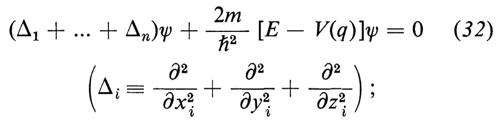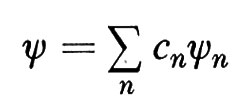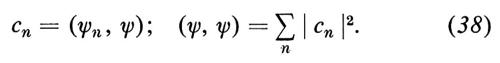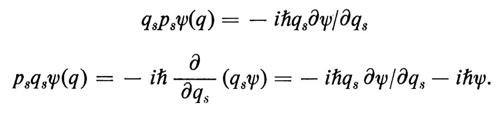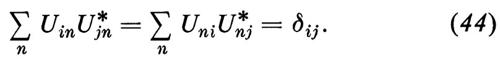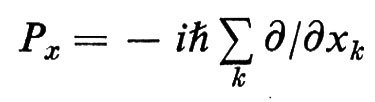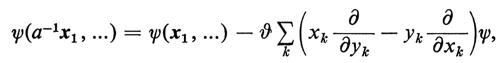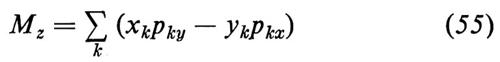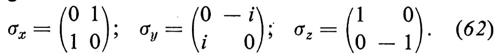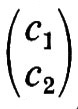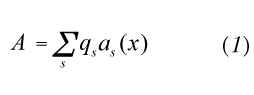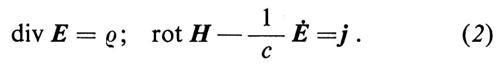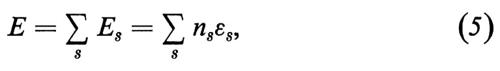Quanti, teoria dei

Quanti, teoria dei

Meccanica quantistica, di Gian Carlo Wick

Elettrodinamica quantistica, di Gian Carlo Wick

Meccanica quantistica

SOMMARIO: 1. Introduzione: a) il quanto d'azione; b) origini della teoria dei quanti; c) gli stati stazionari di Bohr; d) diffusione elastica e anelastica degli elettroni; e) il princioio di corrispondenza e lo spettro dell'atomo di idrogeno; f) regole di quantizzazione di Bohr-Sommerfeld. □ 2. Onde e particelle, esperienze cruciali: a) il dilemma; b) onde di de Broglie; c) interpretazione statistica delle ampiezze d'onda; d) effetto Compton, metodo delle coincidenze. □ 3. Meccanica quantistica: a) scoperta della teoria; b) problemi agli autovalori; c) l'equazione d'onda di Schrödinger; d) interpretazione statistica della funzione d'onda; e) equazione e funzioni d'onda per un sistema di n corpi; f) momento angolare intrinseco (spin) dell'elettrone, principio di esclusione. □ 4. Principi generali della meccanica quantistica: a) vettori di stato, operatori hermitiani; b) algebra degli operatori, commutatori; c) teoria delle trasformazioni; d) rappresentazione di Heisenberg. □ 5. Simmetrie o principi di invarianza nella meccanica quantistica: a) gruppi di trasformazioni delle coordinate; b) trasformazioni unitarie della funzione d'onda, leggi di conservazione; c) rappresentazioni, algebra di Lie; d) parità; e) formule di intensità, regole di selezione. □ 6. Formulazione relativistica: a) operatori di simmetria del gruppo di Lorentz inomogeneo; b) l'equazione di Dirac; c) problemi della meccanica quantistica relativistica. □ Bibliografia.

1. Introduzione.

a) Il quanto d'azione.

La ‛teoria dei quanti' esprime i concetti fondamentali e le leggi dinamiche della fisica in una forma compatibile con l'esistenza del ‛quanto d'azione' o costante di Planck h, una costante fisica universale che ha dimensioni [energia × tempo]. L'abbreviazione ℏ = ℏ/2π è oggi frequente; in unità c.g.s. h ha il valore:

ℏ = 1,0546 × 10^-27 erg 5 (≃ 10^-34 J s).

Una revisione delle idee della dinamica e dell'elettrodinamica classiche si era già iniziata al principio del secolo, quando la velocità della luce c nel vuoto era stata riconosciuta come limite superiore fondamentale alla velocità di propagazione di qualsiasi interazione (v. relatività). Eppure la revisione connessa con la costante h è ancora più radicale; sotto uno dei suoi aspetti la costante h è un quantum, nel senso di unità indivisibile, laddove la descrizione classica fa uso di variabili continue (esempi di grandezze che diventano ‛quantizzate' sono le componenti della quantità di moto angolare e l'integrale di ‛azione' su un'orbita periodica). Sotto un altro aspetto, anche più sorprendente, la costante h appare come l'anello di congiunzione fra interpretazioni della realtà fisica reciprocamente incompatibili dal punto di vista classico. Esempi tipici di questo aspetto sono le relazioni di Planck-Einstein e quelle di de Broglie tra gli aspetti corpuscolare e ondulatorio delle radiazioni (v. eqq. 9 e 10). Uno dei principali meriti del formalismo della meccanica quantistica è di esser riuscito a conciliare in un singolo schema coerente questi aspetti ‛complementari' della realtà.

b) Origini della teoria dei quanti.

D'ora in poi chiameremo ‛teoria classica' il quadro dei fenomeni ottici costruito verso la fine del secolo scorso, mediante una fusione della teoria elettromagnetica di Maxwell con la dinamica newtoniana delle particelle. Si ammetteva che la luce, o più generalmente la radiazione (infrarossa, visibile o ultravioletta), consistesse di onde elettromagnetiche di varia frequenza, le quali interagissero con la materia soprattutto grazie alla presenza, entro ogni atomo o molecola, di particelle cariche di massa piccolissima (elettroni). In base alla ben nota stabilità di atomi e molecole, era naturale supporre che questi elettroni fossero legati a posizioni di equilibrio. Consideriamo brevemente le conseguenze di queste ipotesi. Quando un elettrone oscilla intorno a una posizione di equilibrio con una certa frequenza, esso agisce come un dipolo di Hertz, emettendo un'onda sferica elettromagnetica della stessa frequenza; in questo modo, può venir trasferita energia dalla materia al campo elettromagnetico (emissione). Se la forza che lega ogni elettrone alla sua posizione di equilibrio è esattamente proporzionale allo spostamento, le oscillazioni saranno strettamente armoniche e la radiazione emessa dagli atomi consisterà di componenti monocromatiche (linee spettrali), come si osserva sperimentalmente. D'altra parte il campo elettrico di un'onda incidente, di frequenza v, può mettere in moto gli elettroni trasferendo energia nel senso opposto al precedente (assorbimento). L'effetto è assai più forte quando ν coincide con la frequenza di oscillazione spontanea di qualche elettrone ('assorbimento di risonanza'). L'elaborazione di queste idee, dovuta in buona parte a H. A. Lorentz (teoria degli elettroni), dà inoltre un quadro particolareggiato di molti altri fenomeni ottici (diffusione, rifrazione, ecc.).

Le prime forti deviazioni dalla teoria classica vennero osservate verso la fine del secolo scorso nell'emissione di luce da parte di sostanze ad alta temperatura. Il problema teorico centrale consisteva nell'interpretazione della distribuzione spettrale della radiazione in equilibrio termico alla temperatura assoluta T (ossia della funzione ρ_ν(T) definita come la densità di energia radiativa di frequenza v, per unità di volume e di intervallo di frequenza). La distribuzione prevista classicamente (la cosiddetta formula di Rayleigh-Jeans) è in accordo con l'esperienza alle basse frequenze, ma è errata alle alte frequenze. L'esperienza conferma invece una formula proposta da Planck nel 1899, che dà la distribuzione spettrale ρ_ν(T) della cosiddetta ‛radiazione di corpo nero'.

in questa celebre formula le costanti α e β sono connesse alle costanti universali c, h e k : α = 8πhc^-3, β = hk^-1 (k è la costante di Boltzmann = 1,38 × 10^-16 erg/⁰K). Le misure di Rubens nell'infrarosso diedero la prima verifica accurata della formula di Planck. Da allora la sua validità non è mai stata messa seriamente in questione.

In breve tempo Planck riconobbe l'origine delle difficoltà teoriche nel fallimento della formula statistica classica, = kT, per l'energia media Ä di un oscillatore armonico unidimensionale a temperatura T. Il passo decisivo (dicembre 1900) viene compiuto con un'audace innovazione nel calcolo di Ä; invece della tradizionale distribuzione continua (di Boltzmann) nello spazio delle fasi, Planck suppone che l'energia di eccitazione di un oscillatore di frequenza ν non possa essere altro che un multiplo di un certo ‛quanto di energia' ε proporzionale alla frequenza,

ε = hv, (1)

e ottiene così per Ä una formula che conduce alla sua legge della radiazione.

È chiaro che una relazione come la (1) è del tutto estranea alla fisica classica; ma il suo pieno significato si rivela solo nelle formulazioni successive di Einstein (1905) e di Bohr (v., 1913). Secondo Einstein la ‛quantizzazione' del moto oscillatorio armonico deve essere un fatto di importanza generale; si deve applicare, per esempio, al moto oscillatorio di atomi o molecole legati elasticamente entro un cristallo; il che conduce a una comprensione profonda delle proprietà termodinamiche dei solidi a bassa temperatura (calori specifici anomali, principio di Nernst, ecc.). Ancor più importante è la ‛concezione euristica' dei fenomeni di emissione ε assorbimento della luce proposta da Einstein, concezione che precisa notevolmente l'ipotesi originale di Planck. Quando un ‛oscillatore' entro un atomo emette un quanto ε di radiazione, non possiamo descrivere il processo mediante l'immagine classica di un'onda sferica emessa. Ciò condurrebbe a gravi paradossi; per esempio: l'energia totale e dell'onda è distribuita in tutte le direzioni; se l'onda si espande radialmente, diventando sempre più debole, come può l'intero quanto di energia raccogliersi di nuovo in un punto lontano quando avviene l'assorbimento? Da questa e da altre argomentazioni, fondate sulla teoria delle fluttuazioni di energia, Einstein deduce che i quanti della radiazione devon venir concepiti come corpuscoli, detti anche ‛fotoni', che si muovono alla velocità della luce. Poiché secondo le leggi della meccanica relativistica tali corpuscoli debbono possedere una quantità di moto p = ε/C e poiché l'emissione è unidirezionale, l'atomo emittente deve ricevere un impulso ε/C nella direzione opposta.

L'esistenza di questo impulso fu verificata direttamente assai più tardi (nel 1933), mediante la tecnica dei raggi molecolari, da R. Frisch. Quando propose la ‛concezione euristica', Einstein poteva solo citare a suo sostegno alcuni risultati qualitativi di P. Lenard sull'emissione fotoelettrica da parte di superfici metalliche. Questi mostravano che la luce di bassa frequenza v non è in grado di estrarre elettroni, indipendentemente dalla sua intensità. Dal punto di vista classico questo comportamento è incomprensibile. Viceversa, se si ammette che l'emissione di un elettrone sia dovuta all'assorbimento di un singolo quanto hv, viene spontaneo pensare che i quanti di bassa frequenza non posseggano sufficiente energia per estrarre un elettrone. Perseguendo quest'idea fino in fondo Einstein predisse: a) l'esistenza di una netta ‛soglia' ν₀ dell'effetto fotoelettrico, dove hv₀, il lavoro di estrazione, misura per ogni metallo il valore minimo dell'energia di legame di un elettrone; b) l'esistenza di un limite superiore h(ν − ν₀) per lo spettro di energia cinetica degli elettroni estratti da luce di frequenza ν. Queste previsioni furono brillantemente verificate da Millikan nel 1916; si ebbe così anche la prima misura di precisione della costante di Planck.

c) Gli stati stazionari di Bohr.

Con il lavoro di N. Bohr (v., 1913) si compie un altro passo in avanti. Egli parte dalla necessità di riconciliare le proprietà più elementari degli atomi, come la loro caratteristica stabilità, con il modello nucleare di Rutherford (v. atomo), secondo il quale ogni atomo consiste di un nucleo pesante, carico positivamente, circondato da un sistema di elettroni tenuti insieme dall'attrazione coulombiana del nucleo. Grazie all'analogia tra la legge di Coulomb e la gravitazione newtoniana, un tale sistema presenta una notevole somiglianza con il sistema planetario.

Le principali difficoltà cui va incontro questo modello sono sufficientemente illustrate dal più semplice sistema di questo genere, l'atomo di idrogeno, consistente di un singolo elettrone di carica −e e massa m (e = 4,803 × 10^-10 u.e.s., m = 0,911 × 10^-27 g) circolante intorno a un protone di carica + e e di massa m_p = 1.836 m. Se trascuriamo per il momento la forza reattiva dovuta all'emissione di radiazione e altre piccole correzioni, possiamo mostrare che l'elettrone si muove su un'orbita periodica ‛kepleriana'; l'asse maggiore 2a, l'energia totale (potenziale + cinetica) E e il periodo di rivoluzione T relativi a tale orbita sono legati dalle relazioni:

dove ω = 2π/T è la velocità angolare media, che in base alla seconda equazione vana proporzionalmente ad a^-3/2. Si noti che T ∝ a^3/2 è la terza legge di Keplero. Si noti anche, per il seguito, la relazione: ω ∝ ∣ e ∣^3/2.

Orbene, un fatto notevole è che, se in queste formule si pone 2a uguale al diametro osservato dell'atomo di idrogeno (2a ≃ 1 Å = 10^-8 cm), se ne deducono per ∣ E ∣ e ω valori grosso modo corretti per l'energia ‛di ionizzazione' e per la frequenza dell'assorbimento di risonanza dell'idrogeno. D'altra parte si può vedere che, per ragioni puramente dimensionali, il modello stesso non possiede una lunghezza caratteristica; senza fare uso di dati sperimentali, le dimensioni dell'orbita rimangono completamente arbitrarie. Un'obiezione ancor più seria nasce, come Bohr fa notare, quando si considerano gli effetti radiativi; infatti la forza di reazione radiativa, benché molto piccola, a lungo andare fa sì che il sistema sia completamente instabile. Questa difficoltà è dovuta sostanzialmente al fatto che l'eq. (2) non pone alcun limite inferiore all'energia E (attribuendo un raggio finito al protone, si può introdurre nel problema una lunghezza ‛fondamentale' e con essa anche un limite inferiore all'energia E della (2); esperimenti sulla diffusione delle particelle, e anche di elettroni, indicano tuttavia che tale raggio finito è così piccolo da non essere pertinente in questa discussione). Ne segue che l'emissione di radiazione è sempre possibile, con una graduale contrazione dell'orbita. Poiché dipende da a, lo spettro emesso sarebbe ‛continuo' e ciò comporterebbe un'altra difficoltà.

Invece di attribuire queste difficoltà al modello di Rutherford, Bohr ne scorge la radice nei difetti delle leggi dell'elettrodinamica classica già rivelati dall'analisi di Planck e Einstein. Il rimedio deve dunque consistere nella ‛quantizzazione' del moto dell'elettrone. In primo luogo si introduce così nel problema una nuova costante, cioè ℏ, che insieme a e ed m definisce una lunghezza, il cosiddetto raggio di Bohr

a_B = ℏ²/me² = 0,529 × 10^-8 cm, (3)

il quale, cosa assai notevole, è dell'ordine di grandezza delle dimensioni atomiche osservate. Dobbiamo inoltre aspettarci che le ‛regole di quantizzazione', quali che siano, permettano, tra tutte le possibili orbite classiche, una particolare successione di orbite; trovare le corrette regole di quantizzazione rappresenta naturalmente una non semplice estensione della prescrizione originale di Planck (che vale solo per un moto armonico). Il modo in cui Bohr affronta questo problema, sebbene di notevole interesse storico, non può venir qui riassunto adeguatamente. Tra le numerose idee nuove che Bohr utilizza, vi sono: a) due postulati fondamentali, che hanno superato indenni la totale revisione della teoria effettuata negli anni 1925-1926; b) l'altrettanto fondamentale ‛principio di corrispondenza'; c) vari principi particolari, che, essendo poi stati notetevolmente estesi e perfezionati da A. Sommerfeld, sono ora noti come ‛regole di quantizzazione di Bohr-Sommerfeld'.

I due postulati di Bohr sono i seguenti.

A. Ogni atomo possiede una successione discreta di valori possibili dell'energia o ‛livelli energetici':

E₁, E₂, E₃, . (4)

(in ordine crescente; il livello più basso, E₁, è chiamato stato fondamentale).

B. L'atomo può compiere ‛transizioni' da un livello energetico a un altro; la differenza di energia viene emessa o assorbita sotto forma di un quanto di luce di frequenza ν. La conservazione dell'energia nell'atto elementare di emissione o di assorbimento viene espressa dalla condizione di Bohr

hν = E_n − E_m, (5)

dove E_n ed E_m sono rispettivamente il livello superiore e il livello inferiore tra cui avviene la transizione (v. fig. 1).

Anche dopo che l'applicazione della meccanica quantistica è stata estesa dal campo atomico a quello dei fenomeni nucleari i due postulati hanno conservato la loro validità. Dovunque nel seguito si parli di livelli atomici, righe spettrali ecc., si può anche intendere: livelli nucleari, righe dello spettro γ, ecc.

Il postulato A non fa altro che affermare più esplicitamente l'idea che in un sistema legato son possibili soltanto certi movimenti ‛quantizzati', mentre il postulato B spinge alle estreme conseguenze le idee di Planck e di Einstein sull'emissione e sull'assorbimento della luce. (Bohr ammette, in via provvisoria, che le stesse orbite, sia pure quantizzate, siano descritte dalla dinamica classica; il postulato B rappresenta pertanto una deviazione più radicale dalla dinamica classica che non il postulato A, ma è solo con la meccanica quantistica del 1925-1926 che si arriva a un distacco completo dalla nozione classica di orbita).

La (5) implica naturalmente che gli spettri atomici sono spettri di righe (non ‛continui'); per di più essa riassume in modo estremamente compatto una quantità sorprendente di fatti sperimentali (alcuni dei quali verranno discussi più avanti: v. cap. 1, ÈÈ d ed e).

In particolare essa fornisce un'interpretazione tanto semplice quanto profonda di certe regolarità ben note già da lungo tempo agli spettroscopisti e riassunte nel ‛principio di combinazione' (v. atomo). Tale principio afferma che l'inverso della lunghezza d'onda, o ‛numero d'onda' ν/c di ogni riga spettrale può venire espresso come differenza tra due ‛termini' di un sistema (di termini) caratteristico dell'atomo emittente. La (5) dice infatti proprio questo, fornendo inoltre l'informazione preziosa che i ‛termini', a meno del fattore hc, sono null'altro che i livelli energetici dell'atomo.

d) Diffusione elastica e anelastica degli elettroni.

Una conferma diretta dell'esistenza di questi livelli energetici discreti fu raggiunta nello stesso anno 1913 con gli esperimenti di J. Franck e G. Hertz; tecniche elettroniche più progredite permisero in seguito non solo di mostrare con grande chiarezza l'esistenza dei livelli, ma anche di misurarli accuratamente (si noti che vi sono analoghe esperienze, a energie assai più alte, in cui si usano elettroni, protoni, ecc. come particelle incidenti, per dimostrare l'esistenza dei livelli energetici del nucleo).

In un tipico esperimento un fascio parallelo di elettroni, di energia cinetica W₀ ben definita, incide su un gas di atomi di una data specie. Rispetto alle velocità elevate degli elettroni, gli atomi si possono considerare praticamente fermi. Si suppone inoltre che essi siano ‛freddi', cioe tutti nello stato fondamentale. Si osserva che gli elettroni diffusi secondo una direzione che forma un angolo ϑ col fascio incidente si suddividono in generale in vari gruppi discreti monoenergetici. Partendo dai principi di conservazione dell'energia e della quantità di moto nell'urto di un elettrone con un atomo e applicando il postulato A di Bohr, si prevede che, a prescindere da una piccolissima correzione dipendente da ϑ e dovuta all'impulso che l'atomo riceve nel suo insieme, il gruppo più energetico di elettroni diffusi abbia la stessa energia W₀ degli elettroni incidenti (diffusione ‛elastica'); analogamente, le differenze W₀ - W₁, W₀ − W₂ ... tra W₀ e le energie W₁, W₂ ... dei gruppi di elettroni diffusi anelasticamente dovrebbero coincidere con le ammissibili energie di eccitazione dell'atomo, E₂ - E₁, E₃ − E₁, ..., dedotte dallo spettro ottico. È esattamente quello che si trova; inoltre la presenza di gruppi diffusi anelasticamente è accompagnata (come prevede la teoria) dall'emissione di righe spettrali corrispondenti a transizioni dell'atomo eccitato a livelli più bassi.

e) Il principio di corrispondenza e lo spettro dell'atomo di idrogeno.

L'esempio più semplice e più famoso del principio di combinazione fu scoperto nel 1885 da Balmer, il quale mostrò che le quattro righe dell'idrogeno allora note potevano essere rappresentate assai accuratamente da una semplice formula aritmetica; essa prevede in realtà, con grande esattezza, centinaia di altre righe scoperte più tardi. La formula si può ottenere dalla (5), se a questa si aggiunge l'informazione che i livelli energetici dell'idrogeno sono dati da:

dove

R = 109.678 cm^-1 (7)

è una costante ed n = 1, 2, 3,... è un intero, detto anche ‛numero quantico principale'. R è la ‛costante di Rydberg' per l'idrogeno e dovrebbe venir designata più esattamente con R_H. Vi sono costanti analoghe per altri sistemi ‛idrogenoidi' (gli ioni He⁺, Li⁺⁺, ecc.). Le lievi differenze tra queste costanti sono elegantemente spiegate dalla teoria di Bohr come effetti del moto relativo, il che tra l'altro fornisce un'impressionante conferma della teoria.

Per il momento considereremo la (6) come ottenuta dallo spettro di righe osservato mediante la (5). Una conferma diretta di questi livelli si potrebbe anche avere dalle citate esperienze di urto anelastico. Ammettendo dunque la (6) come un fatto sperimentale, vedremo ora che il valore della costante R si può dedurre a priori dal principio di corrispondenza, il quale afferma che le frequenze di Bohr date dall'eq. (5) devono coincidere asintoticamente (cioè nel caso limite di grandi numeri quantici) con le frequenze previste dall'elettrodinamica classica.

Per capire cosa ciò significhi, immaginiamo che l'elettrone si muova attorno al protone in un'orbita kepleriana con un'energia E = E_n, corrispondente a un grande valore del numero quantico' n. Nota l'energia E, possiamo calcolare mediante la (2) l'asse maggiore 2a e il periodo T = 2π/ω dell'orbita; si noti che a varia come n²: a valori elevati di n corrispondono quindi orbite di grandi dimensioni (v. atomo).

Secondo la teoria classica, un tale elettrone dovrebbe irraggiare in primo luogo come un dipolo hertziano oscillante con la frequenza fondamentale ν = 1 /T. Questa sarebbe l'unica frequenza emessa se l'orbita fosse circolare; ma, essendo l'orbita ellittica, lo sviluppo in serie di Fourier del momento di dipolo in funzione del tempo contiene anche le ‛armoniche superiori', 2ν, 3ν,..., ecc. Lo spettro'classico' contiene dunque tutte queste frequenze.

Confrontiamo questo spettro con la formula di Bohr (5). Nelle transizioni dallo stato E_n a stati più bassi, E_n-1, E_n-2, ..., ecc., le frequenze emesse sono:

A prima vista questo non ha nulla a che vedere con lo spettro classico, ma quando n è assai grande vi sono due sorprese. Per k = 1, 2, 3,... (piccolo rispetto a n) si ha approssimativamente:

ν_k ≃ (2R/n³)k ≃ kν₁,

e cioè ν₂, ν₃, ... sono effettivamente (quasi esattamente) le armoniche superiori di ν₁; per di più, ν₁ ~ n^-3 ∝ ∣ E ∣^3/2, oc E 13/2, il che è proprio la relazione classica, notata precedentemente, tra frequenza ed energia dell'orbita. È dunque possibile scegliere il valore di R in modo tale che i due spettri coincidano riga per riga nel limite n → ∞. Si calcola facilmente che il valore in questione si ottiene da:

Rhc = me⁴/(2 ℏ²); (8)

più esattamente, date le approssimazioni fatte nella (2), la (8) dà il valore R_∞ della costante di Rydberg ‛per un nucleo infinitamente pesante'.

Un esame critico della validità sperimentale di questa formula, entro i limiti oggi permessi dall'elevatissima precisione delle misure, va oltre i confini di questo articolo. Basti dire che la formula è stata e rimane uno dei trionfi della teoria di Bohr.

f) Regole di quantizzazione di Bohr-Sommerfeld.

Omettendo altre importanti applicazioni del principio di corrispondenza (intensità delle righe spettrali, regole di selezione), passiamo alla deduzione completa dell'eq. (6), compresa la dipendenza dal numero n. Molti eminenti fisici oltre Bohr, fra i quali in modo particolare A. Sommerfeld, presero parte alla soluzione del difficile problema di trovare ‛regole di quantizzazione' soddisfacenti. A tale scopo furono fatte varie considerazioni, tra cui forse la più stringente era quella fondata sul ‛principio adiabatico', introdotto da P. Ehrenfest per motivi termodinamici, in base al quale le regole di quantizzazione devono esser tali da restare invariate dopo una trasformazione adiabatica, cioè dopo una variazione infinitamente lenta di qualche parametro esterno, come, ad esempio, un campo elettrostatico o magnetostatico in cui il sistema sia immerso. La regola assai semplice usata da Bohr afferma che il momento angolare dell'elettrone nella sua orbita, 2πmab/T (dove b è l'asse minore dell'ellisse), dev'essere un multiplo intero di h/2π. Per un'orbita circolare (a = b) questa condizione determina i livelli energetici in accordo con l'eq. (6), in cui il valore della costante R è fornito dalla (8). In questo caso (ma solo in questo) n coincide nella teoria di Bohr con l'intero che misura il momento angolare. Quando a ≠ b la regola di cui sopra, pur rimanendo vera, non basta a fissare il valore dell'energia. La condizione necessaria, nella sua forma più semplice, si riconnette al ‛principio di minima azione' di Leibniz e Maupertuis. Essa afferma che l'integrale d'azione, ossia l'integrale di linea della quantità di moto, esteso all'intera orbita chiusa, è un multiplo intero della costante di Planck:

§ mv ds = nh; (9)

nella (9) v è la velocità dell'elettrone e ds è l'elemento di linea. Si hanno così due numeri quantici, uno dei quali determina l'energia e l'altro il momento angolare. Insieme essi determinano l'eccentricità dell'orbita. L'orientamento spaziale del piano dell'orbita rimarrebbe così ancora interamente arbitrario. Esso viene definito da un'ulteriore condizione, usata da Sommerfeld e da altri nella discussione di effetti dovuti a campi esterni, come l'effetto Zeeman (v. atomo). Il successo di questa cosiddetta ‛quantizzazione spaziale' nello studio di questi effetti e la sua verifica diretta nella famosa esperienza di Stern e Gerlach sono pietre miliari nella storia della teoria dei quanti.

2. Onde e particelle, esperienze cruciali.

a) Il dilemma.

Una questione, più di ogni altra, fu oggetto di dibattito nei primi due decenni di sviluppo della teoria dei quanti: come si poteva eliminare una contraddizione così netta come quella tra i diversi aspetti della luce? Come si è detto, le prove in favore di un'interpretazione strettamente corpuscolare dei fenomeni di emissione e assorbimento sono schiaccianti; ma le ben note difficoltà che questa interpretazione incontra nelle classiche esperienze di interferenza e diffrazione sono molto gravi: il passo dall'osservazione di questi fenomeni a un'interpretazione mediante onde che si sovrappongono linearmente è troppo diretto e naturale perché se ne possa fare a meno. Questo dilemma divenne noto come ‛dualismo onda-particella'.

Di particolare interesse a questo riguardo è il fatto sperimentale che le frange chiare e scure, osservate su uno schermo (o meglio su una lastra fotografica) in uno dei tanti dispositivi interferenziali, rimangono essenzialmente invariate al variare dell'intensità luminosa, anche quando essa è talmente bassa che gli arrivi dei singoli quanti sulla lastra sono nettamente separati nel tempo. L'energia di un singolo quanto, beninteso, non è distribuita in modo continuo sullo schermo come quella di un'onda classica; essa appare invece di colpo tutta in un punto. Tuttavia le frange devono avere una relazione ben definita con il comportamento dei singoli quanti, nel senso statistico seguente: il punto d'arrivo varia a caso da un quanto all'altro, ma con una distribuzione di probabilità tale che, dopo un'esposizione sufficientemente lunga (cioè dopo che moltissimi quanti hanno colpito lo schermo), la distribuzione media risultante riproduce esattamente il risultato noto.

Fu della massima importanza per il successivo sviluppo della teoria il fatto che questa contraddizione tra comportamento corpuscolare e ondulatorio si riscontrasse non solo in quelle radiazioni che, come l'ultravioletto e i raggi X, possono considerarsi un'estensione dello spettro visibile ad altre lunghezze d'onda, ma anche, come ora vedremo, in radiazioni di natura del tutto diversa, come i raggi catodici (cioè fasci di elettroni), i raggi atomici o molecolari, i fasci di protoni, neutroni, ecc.: tutte radiazioni a lungo considerate chiaramente e strettamente corpuscolari.

b) Onde di de Broglie.

L'indizio di una possibile natura ondulatoria dell'elettrone fu intravisto nel 1924 da L. de Broglie nella forma della regola di quantizzazione data dall'eq. (9) per un'orbita. Si ammetta per un momento che un fascio parallelo di elettroni, aventi ognuno la stessa energia cinetica w e quantità di moto p, possegga allo stesso tempo, e in un senso che apparirà poi più chiaramente, le proprieta ‛duali' di un'onda piana di frequenza circolare ω = 2πν e lunghezza d'onda λ; dovrà allora esservi, come nel caso dei fotoni, una relazione tra i due aspetti duali della radiazione, relazione che deve valere indipendentemente dal sistema inerziale di riferimento rispetto al quale ν, w, ecc. sono definite (‛invarianza relativistica'). Nel caso dei fotoni questa relazione assume la forma già nota:

ε = hν; ℏω, p = ℏk, (10)

dove la seconda equazione esprime la relazione di Einstein per un fotone p = ε/c = hν/c, sotto forma vettoriale (il ‛vettore d'onda' k, di modulo k = 2π/λ = ω/c, è normale alla superficie di un'onda piana). De Broglie ammise, per analogia, che le stesse relazioni valessero per gli elettroni e le ‛onde' corrispondenti. L'invarianza relativistica delle relazioni viene salvaguardata, ove si ponga ε = w + m₀c², includendo cioè nell'energia e della particella l'energia di riposo m₀c² (nel caso dei fotoni la massa di riposo m₀ è nulla). La lunghezza d'onda di queste ‛onde di de Broglie' è data perciò dalla:

λ = h/p. (11)

Per elettroni non relativistici (v ≪ c) si può inoltre porre p = m₀v.

L'indizio', di cui sopra, è l'analogia, indotta dalla (11), tra la regola quantica (9) per un'orbita chiusa, ossia

§ ds/λ = n, (12)

e la nota condizione 2l/λ = n per le oscillazioni spontanee (onde stazionarie) di una corda vibrante di lunghezza l. L'eq. (12) dice infatti che un'onda di de Broglie che percorre un cammino ricurvo lungo l'orbita si ritrova al punto di partenza con la fase iniziale e può quindi generare un sistema di onde stazionarie. Nasce così la possibilità, sfruttata più tardi da Schrödinger, di interpretare le regole di quantizzazione in un modo del tutto nuovo.

Questa straordinaria intuizione di de Broglie doveva venir ben presto verificata dallo storico esperimento di C. Davisson e L. H. Germer nel 1927. L'eq. (11) mostra che elettroni aventi, per esempio, un'energia cinetica dell'ordine di 100 eV hanno una lunghezza d'onda λ dell'ordine di 108 cm, adatta cioè per esperienze di diffrazione nei cristalli, simili a quelle coi raggi X. Su questo si basa l'esperienza suddetta, come anche la precisa conferma dell'eq. (11) da parte di G. P. Thomson nel 1928. Si ritiene ora, in parte per ragioni teoriche, in parte per via di numerose esperienze sui raggi molecolari (v. Estermann e Stern, 1930), sui neutroni lenti (E. Fermi e altri) ecc., che proprietà ondulatorie rette dalla (11) possano attribuirsi a particelle di qualsiasi genere. Non occorre insistere sul fatto che le proprietà ondulatorie di particelle di dimensioni macroscopiche non sono praticamente osservabili (λ è troppo piccola).

c) Interpretazione statistica delle ampiezze d'onda.

In tutte le esperienze summenzionate la figura di interferenza o di diffrazione osservata è descritta correttamente da un campo d'onde, ma, come si è già osservato, il comportamento individuale delle particelle può venire descritto soltanto in termini statistici: si dirà, per esempio, che la probabilità che un fotone produca una reazione chimica in un certo punto di una lastra fotografica è proporzionale all'intensità del campo in quel punto. Questo punto di vista permette evidentemente di riconciliare l'emissione unidirezionale dei quanti di Einstein con l'onda sferica di dipolo, ammettendo che la distribuzione d'intensità dell'onda nelle varie possibili direzioni determini puramente la probabilità di emissione direzionale del fotone o, se si vuole, che l'intensità dell'onda, là dove si trova un qualche atomo capace di assorbire il fotone, determini la probabilità di assorbimento.

È però tutt'altro che facile vedere come questa interpretazione probabilistica possa conciliarsi con la connessione causale che deve esistere tra la direzione del quanto di luce e il rinculo dell'atomo emittente, come richiede la legge di conservazione della quantità di moto, nell'ipotesi che tale legge sia strettamente valida negli atti individuali di emissione. La difficoltà appare nel modo più chiaro se si suppone che gli atomi siano situati a grande distanza dal punto di emissione; l'atto di assorbimento, che in ultima analisi definisce la direzione del quanto emesso, avviene molto tempo dopo l'atto di emissione. Ora, se esso è determinato solo probabilisticamente, com'è possibile descrivere una sua correlazione esatta con il rinculo dell'atomo, che è già avvenuto assai prima, all'atto dell'emissione?

Vedremo, tuttavia, che le ‛ampiezze di probabilità' generalizzate della meccanica quantistica, per esempio le funzioni d'onda multidimensionali di Schrödinger, possono effettivamente descrivere benissimo correlazioni siffatte; il prezzo di questo progresso è però una rinuncia quasi totale all'ordinaria immagine spazio-temporale dello svolgersi dei fenomeni naturali. Esaminiamo perciò i fatti che rendono inevitabile questo sacrificio.

d) Effetto Compton, metodo delle coincidenze.

Oltre al già citato esperimento di Frisch, prove anche più stringenti della validità delle leggi di conservazione negli atti individuali sono date dallo studio delle ‛coincidenze', per esempio nella diffusione dei raggi X o γ.

Studiando la diffusione di raggi X monocromatici da parte di varie sostanze, H. A. Compton scoprì nel 1923 che i raggi X diffusi sono più ‛molli' della radiazione primaria (hanno cioè lunghezza d'onda maggiore). Per varie ragioni, che omettiamo, la diffusione viene attribuita a elettroni presenti negli atomi del diffusore ed essenzialmente liberi. L'effetto osservato da Compton si interpreta facilmente se si descrive l'atto di diffusione come un urto tra un elettrone allo stato di riposo e un fotone X. Se in seguito all'urto il fotone cambia direzione, le leggi di conservazione richiedono che una certa quantità di moto e quindi anche una certa energia vengano trasmesse all'elettrone. Ne segue che l'energia ε = hν del fotone deve a sua volta diminuire, ossia λ = c/ν deve aumentare. Questa è la spiegazione qualitativa dell'effetto. Un semplice calcolo mostra che la lunghezza d'onda λ′ della radiazione diffusa è data da:

λ′ = λ + (h/m₀c)(1 − cos ϑ), (13)

dove ϑ è l'angolo di diffusione ed m₀ è la massa di riposo dell'elettrone. Questa formula è in perfetto accordo con le misure.

L'importanza cruciale dell'effetto Compton sta anche nella verifica più accurata delle leggi di conservazione fornita da ulteriori studi. L'interpretazione ora data dell'effetto richiede che, ogniqualvolta un quanto X viene diffuso in una certa direzione, un elettrone venga contemporaneamente proiettato in una ben definita direzione, legata alla prima, con una certa velocità. In una ben nota esperienza, Bothe e Geiger mostrarono infatti che un contatore di fotoni e un contatore di elettroni situati in posizione opportuna l'uno rispetto all'altro rivelano l'arrivo simultaneo (in ‛coincidenza') di un elettrone e di un fotone con la frequenza media prevista; in altre posizioni i conteggi dei due contatori non sono correlati nel tempo, si hanno cioè solo coincidenze casuali. L'esistenza delle correlazioni richieste dalle leggi di conservazione dell'energia e dell'impulso è anche confermata da un'esperienza effettuata da Compton e Simon con un diverso apparato; le tecniche elettroniche moderne hanno permesso una conferma dei risultati di Bothe e Geiger in condizioni assai più probanti. Come vedremo questi risultati hanno una parte importante nell'interpretazione del formalismo ondulatorio nella meccanica quantistica.

3. Meccanica quantistica.

a) Scoperta della teoria.

Le enormi difficoltà incontrate nel tentativo di estendere le regole di quantizzazione di Bohr-Sommerfeld a sistemi più complicati (atomi con più elettroni) fornirono in parte la spinta alla scoperta, nel 1925-1926, della meccanica quantistica. Il carattere provvisorio delle regole era stato del resto riconosciuto da alcuni sin dal principio; la ricerca di uno schema più coerente era quindi inevitabile.

La nuova struttura fu scoperta seguendo due vie assai diverse e in due forme distinte: meccanica delle matrici e meccanica ondulatoria, che vennero poi riconosciute come diversi aspetti di un'unica struttura. Lungo una di queste vie il passo decisivo fu compiuto da W. Heisenberg nell'estate del 1925. (Per la parte avuta da altri fisici, in particolare M. Born, P. Jordan, P. A. M. Dirac e W. Pauli, ai quali si devono contributi essenziali, v. van der Waerden 1967).

Il formalismo di Heisenberg si presenta come un analogo dello sviluppo in serie di Fourier per un'orbita periodica. In tale sviluppo il moto di una particella appare come una sovrapposizione di moti armonici di frequenza ν, 2ν, 3ν, ... La frequenza ‛fondamentale' ν dipende in generale, com'è ovvio, dall'orbita (cioè dai numeri quantici che definiscono lo stato stazionario). Le ampiezze dei moti armonici componenti sono i classici coefficienti di Fourier. Si noti che l'intera impalcatura del metodo di Bohr-Sommerfeld (e cioè le equazioni classiche del moto e le regole quantiche) si può mettere sotto la forma di una serie di relazioni tra i coefficienti di Fourier e le relative frequenze. L'idea di Heisenberg fu di sostituire, in queste relazioni, le componenti armoniche classiche con un insieme ‛corrispondente' di componenti, le cui frequenze sono quelle fisicamente osservabili date dalla relazione di Bohr e le cui ampiezze, come le relative frequenze, sono assegnate ognuna a una determinata transizione tra due stati stazionari. Il modo naturale di assegnare indici a queste ampiezze è perciò di disporle in una matrice, le cui righe (e le cui colonne) sono numerate in corrispondenza con i livelli energetici E₁, E₂, E₃, ... Le componenti armoniche, per esempio, della coordinata x di un elettrone diventano così elementi di matrice, la cui dipendenza dal tempo è data dalla:

x_nm(t) = x_nm(0)e^iωnmt, (14)

dove ω_mn è 2π volte la frequenza ν dell'eq. (5), cioè ω_nm = (E_n − E_m)/ℏ. In particolare gli elementi ‛diagonali' non dipendono dal tempo (poiché ω_nn = 0), ma rappresentano valori medi, rispetto al tempo, negli stati corrispondenti. Questa nuova assegnazione di indici alle componenti armoniche ci costringe a modificare le equazioni in certi modi che sono dettati da requisiti di compatibilità. L'audacia di questo procedimento appare chiaramente, ove si osservi che, poiché i moti armonici componenti sono ora assegnati non a uno stato stazionario ben definito, ma a transizioni, essi non si possono più ricomporre in un moto classico ben definito, sicché la nozione di ‛orbita' viene a perdere il suo senso preciso; infatti, per piccoli numeri quantici, tale nozione è del tutto priva di significato.

L'altra via di approccio al formalismo quantistico, partendo dalle idee di de Broglie, conduce alla meccanica ondulatoria di E. Schrödinger (1926). In breve l'idea chiave è che la dinamica classica non è una teoria esatta, ma presuppone grosso modo lo stesso tipo di approssimazioni che presenta l'ottica geometrica rispetto all'ottica ondulatoria. Nello studio dei movimenti elettronici entro l'atomo queste approssimazioni diventano troppo grossolane e la dinamica classica deve venir sostituita con una teoria di tipo ondulatorio. È chiaro che l'ipotesi di de Broglie è il primo passo in questa direzione; è solo un primo passo, perché l'idea si deve esprimere in una forma precisa mediante un'equazione delle onde' e ancor più perché, come si vedrà più avanti, la concezione generale di una meccanica ondulatoria implica un'estensione del problema degli n corpi tutt'altro che banale. Esaminiamo dapprima il caso di un solo elettrone, ossia, in pratica, il problema dell'idrogeno.

b) Problemi agli autovalori.

La prima pubblicazione di Schrödinger è intitolata La quantizzazione come problema agli autovalori; essa contiene la formulazione matematica precisa dell'analogia di de Broglie tra la (9) e una condizione per la formazione di onde stazionarie.

È ben noto che nella fisica matematica classica problemi del genere assumono la forma seguente. Il campo d'onda è descritto da una funzione d'onda ψ(x, y, z, t) che obbedisce a un'equazione lineare omogenea alle derivate parziali, a coefficienti costanti. Il carattere lineare omogeneo dell'equazione dà luogo al ‛principio di sovrapposizione': due o più soluzioni si possono combinare linearmente, ottenendo così ancora una soluzione. Ciò è fondamentale per i fenomeni di interferenza. Nel caso delle onde stazionarie, ψ è una funzione sinusoidale del tempo, il che si può scrivere, mediante note convenzioni, nella forma ψ = u(x, y, z) e^-iωt; la funzione u soddisfa allora un'equazione indipendente dal tempo (o ‛stazionaria'), in cui la frequenza ν = ω/2π appare come parametro. Si studiano di solito onde stazionarie in una cavità racchiusa da pareti riflettenti; la funzione d'onda deve soddisfare, sulle pareti, ‛condizioni al contorno' omogenee, che assicurano la riflessione totale delle onde. Si trova allora che l'equazione d'onda, insieme alle condizioni al contorno, possiede soluzioni non nulle solo per una serie discreta di valori del parametro frequenza. La ricerca di questi ‛autovalori' e delle corrispondenti soluzioni dell'equazione, le ‛autofunzioni', costituisce il problema agli autovalori.

Il caso più noto e più semplice è quello, unidimensionale, della corda vibrante, che conduce all'equazione di

D'Alembert:

in cui ν è una costante che rappresenta anche la velocità di propagazione delle onde. Per un'onda stazionaria, ψ = e^-iωtu(x), l'equazione diventa:

ove k = ω/v è il parametro di cui si cercano gli autovalori. Con le condizioni al contorno corrispondenti a una corda di lunghezza l tenuta fissa agli estremi si ritrovano facilmente gli autovalori

k = k_n = (π/l)n (n = 1, 2, 3, ...), (17)

ossia, poiché k = k_n = 2π/λ la condizione 2l = nλ già citata. Anche più interessante per noi è l'analogo tridimensionale della (15), in cui la derivata seconda rispetto a x è sostituita dal laplaciano; la (16) diventa allora

Notiamo infine il caso in cui la v è una funzione della posizione (mezzo a indice di rifrazione variabile da punto a punto). In questo caso, per una data aω, si ha nella (18) k = ω/v = k₀n(x, y, z), ove k₀ è una costante.

Possiamo aspettarci che le onde stazionarie di de Broglie siano descritte da un'equazione in cui l'energia appare come parametro, dato che nella teoria dei quanti ‛energia' è sinonimo di ‛frequenza'; i livelli energetici sono gli autovalori di questo parametro, secondo l'intuizione di de Broglie. Questo è un modo di ‛quantizzare' assai più naturale, dal punto di vista matematico, di quanto non sia l'arbitraria imposizione di regole quantiche alle orbite classiche voluta dalla teoria di Bohr-Sommerfeld. Nell'atomo di idrogeno non vi sono, beninteso, pareti riflettenti che racchiudano le onde in una regione finita, ma, come vedremo, una ‛condizione al contorno all'infinito' svolge un ruolo equivalente, cosicché si trova effettivamente uno spettro discreto di autovalori negativi del parametro energia e precisamente i livelli che già conosciamo. L'equazione possiede inoltre uno spettro continuo di autovalori positivi, che corrispondono alle orbite iperboliche della teoria classica. Le autofunzioni corrispondenti a questi valori positivi dell'energia sono indispensabili nella teoria dell'urto di elettroni (o analogamente di altre particelle cariche) contro un nucleo. Su di esse si basa, per esempio, la deduzione ondulatoria sia della formula di Rutherford, sia di certe deviazioni interessanti nel caso dell'urto tra particelle identiche.

c) L'equazione d'onda di Schrödinger.

Le onde di de Broglie seguono una ‛legge di dispersione', cioè una relazione tra frequenza e lunghezza d'onda che le distingue da altri casi. La legge segue dalla (10) e dalla relazione tra energia 8 e quantità di moto p per una particeila:

ε ≡ m₀c² + E = c(m₀²c² + p²)^1/2 (19)

(E è l'energia cinetica). Si vede subito che ω non è proporzionale al numero d'onda k, di modo che l'equazione d'onda per le onde di de Broglie dev'essere diversa dalla versione tridimensionale della (15). È opportuno notare che, quando la ‛velocità di fase' ω/k non è una costante (cioè dipende dalla frequenza), essa deve venir distinta dalla ‛velocità di gruppo' dω/dk, la quale, com'è ben noto dall'ottica, è quella che si misura nei metodi detti di ‛durata del volo'; infine la velocità di gruppo coincide, per le onde di de Broglie, con la velocità delle particelle corrispondenti dE/dp = c²p/ε. Vogliamo inoltre un'equazione che sia valida in presenza di un campo elettrostatico. Per semplicità rivolgiamoci subito al caso non relativistico: elettroni di velocità v ≪ c, dunque p ≪ m₀c. Lasciamo cadere la distinzione tra massa m e massa di riposo m₀ e scriviamo p = mv e

E = (p²/2m) + V(x, y, z), (20)

dove, per esempio, nel caso di un elettrone nel campo coulombiano di un nucleo di carica Ze Sito nell'origine, si ha V = − Ze²/r; dunque E è ora l'energia totale (cinetica + potenziale). L'ipotesi più semplice che possiamo fare è che l'equazione d'onda sia del tipo della (18) quando k varia con la posizione nel modo indicato dalle equazioni (10) (11) e (20), ossia

Questa è la famosa equazione di Schrödinger indipendente dal tempo. Supponiamo che la corrispondente funzione d'onda completa sia ψ = e^-iωtu(x, y, z), dove ω = E/ℏ, che si ottiene dalla (10) e dalla (19) trascurando il termine costante ω₀ = m₀c²/ℏ, il che non ha importanti conseguenze. Allora ῼψ/ῼt = − iωψ = −i(E/ℏ)ψ e la (21) diventa:

che è l'equazione che contiene il tempo; questa è più generale della (21), in quanto si applica non solo a onde di frequenza (o energia E) arbitraria, ma anche a sovrapposizioni di onde di varie frequenze.

Si hanno soluzioni esatte dell'eq. (21) per vari tipi di potenziale; se, per esempio,si suppone che sia V = ½k(x² + y² + z²), ossia il potenziale di un oscillatore armonico, si trova una serie di livelli equidistanti, intervallati di ℏω₀, con ω₀ = (k/m)^1/2, in accordo con l'ipotesi di Planck. Nel caso del potenziale coulombiano già detto, V = − Ze²/r, si ritrova la formula di Balmer e così via. Diamo qualche particolare sul caso coulombiano, per via della sua importanza.

Poiché in questo caso V dipende solo da r = (x² + y² + + z²)^1/2, è naturale cercare soluzioni della (21) anch'esse della forma u = χ(r). Si vede subito che la funzione χ deve soddisfare l'equazione

la quale, per E = − Z²Rhc (che per Z = 1 corrisponde allo stato fondamentale dell'idrogeno, v. eqq. 6 e 8), possiede la soluzione:

χ = e^-ξ (ξ = Zr/a_B), (24)

dove a_B è il raggio di Bohr, eq. (3). Anche per Z = 2, 3, ... il livello ora trovato coincide esattamente con la teoria di Bohr. Soltanto, mentre in questa teoria lo ‛stato' è un'orbita circolare di raggio a_BZ^-1, nella meccanica ondulatoria esso è un'onda stazionaria che si estende a tutto lo spazio; siccome però la u decresce esponenzialmente al crescere di r e diventa trascurabile quando r ≫ a_BZ^-1, in pratica il campo d'onda si estende a una regione di dimensioni paragonabili a quelle dell'orbita di Bohr. Si verifica similmente che la (23) ha un'altra soluzione,

χ = e^-ξ/2(1 − ½ξ), (24a)

per un valore E = E₂ = −¹-₄Z²Rhc corrispondente al livello n = 2 dell'eq. (6). Un grafico di queste due soluzioni in funzione della distanza r è dato nella fig. 2. Se si calcolano soluzioni della (23) per un qualsiasi valore di E intermedio tra i due ora considerati (richiedendo inoltre che la soluzione sia finita nell'origine, r = 0), si trova invariabilmente che esse ‛esplodono' esponenzialmente all'infinito (r → ∞): si vedano le linee tratteggiate nella fig. 2. La ‛condizione al contorno all'infinito' ci impone di scartare queste soluzioni come fisicamente prive di significato. Per la stessa ragione si scartano le soluzioni corrispondenti a valori di E al disotto dello stato fondamentale E₁; anche per E al disopra di E₂ le soluzioni esplodono all'infinito, fino a che E non raggiunge il valore E₃, per il quale si trova di nuovo una soluzione accettabile e così via. Così avviene che la condizione al contorno restringa i valori di E a una serie discreta di autovalori.

Un tipo più generale di soluzione si ottiene mediante la ‛separazione delle variabili' in coordinate polari r, ϑ, ϕ, ossia ponendo u = χ(r)Y(ϑ, ϕ). Si trova allora che la Y è necessariamente una ‛funzione sferica' Y₁ , con l = 1, 2, 3, ... (il caso l = 0 è quello trattato precedentemente, poiché Y₀ = cost.). Non si trova, però, in questo modo, alcun nuovo livello. Si trovano soltanto nuove autofunzioni per i livelli n = 2, 3,... già noti (analogamente nella teoria di Bohr-Sommerfeld a un livello possono corrispondere diverse orbite). Più precisamente si trova che al livello E_n corrispondono n² soluzioni linearmente indipendenti. Si dice che questi livelli sono degeneri: solo lo stato fondamentale (n = 1) è non degenere; si noti, tuttavia, che non è qui inclusa un'ulteriore degenerazione, dovuta allo spin dell'elettrone.

Teoremi generali permettono di affermare che gli autovalori E_n e le corrispondenti autofunzioni u_n formano un sistema ‛completo', nel senso che la soluzione generale della (22) si può sviluppare in una serie:

Quando esiste uno spettro continuo di autovalori (per esempio quando è E > 0, per l'atomo di idrogeno) la somma diventa un integrale. Un esempio del genere si ha nel caso di particelle libere (V = 0), quando le autofunzioni della (21) sono semplici esponenziali e^{ik x}. La funzione d'onda è allora una sovrapposizione di onde piane (integrale di Fourier tridimensionale):

dove ω ≡ ω(k) = ℏk²/2m e dk = dk_xdk_ydk_z è l'elemento di volume nello ‛spazio dei momenti'. Sovrapponendo onde piane, si possono costruire in questo modo ‛pacchetti di onda' di dimensioni finite, che in assenza di forze esterne si muovono in linea retta e in presenza di un potenziale V si muovono lungo il cammino ricurvo che la particella percorrerebbe nel caso classico corrispondente. Un teorema di Ehrenfest permette di precisare ulteriormente questa analogia. Un altro modo di mettere in luce la corrispondenza tra meccanica ondulatoria e dinamica classica verrà descritto più avanti.

d) Interpretazione statistica della funzione d'onda.

La funzione ψ è necessariamente complessa, per la presenza dell'immaginario nell'eq. (22). La parte reale e quella immaginaria della ψ potrebbero considerarsi come grandezze fisiche reali o ‛componenti' di un campo nel senso classico. Scbrödinger ha anche mostrato che, mediante questi campi, è possibile costruire una densità di carica ρ e di corrente j, che soddisfino la consueta equazione di continuità: ρ̇ + div j = 0. La densità ρ, per esempio, va posta proporzionale al quadrato del valore assoluto della ψ: ρ ∝ ∣ ψ ∣². Dall'equazione di continuità si deduce che la carica totale è indipendente dal tempo:

∫ ∣ ψ(x, t)∣² dτ = cost (27)

(dτ = dx dy dz). Il ‛campo ψ' può dunque trasportare una carica, il cui segno e valore totale per un pacchetto d'onde sono ancora a nostra scelta. Un pacchetto di carica totale −e (la carica dell'elettrone) potrebbe quindi considerarsi come un interessante modello dell'elettrone. Quest'idea però non regge a un esame critico. Un pacchetto d'onde non possiede la stabilità necessaria a rappresentare l'indivisibilità della carica di un elettrone; urtando contro un ostacolo, esso si sbriciola in tutte le direzioni e, del resto, anche senza urti, a lungo andare un pacchetto d'onde di de Broglie non sta insieme. Sostanzialmente le difficoltà sono poi le stesse già incontrate nel tentativo di descrivere i fotoni come pacchetti d'onde del campo maxwelliano interpretato in senso classico.

D'altra parte l'interpretazione ‛statistica' della funzione ψ, proposta da Born, come ‛ampiezza di probabilità' ci dà una descrizione logicamente coerente del comportamento di un elettrone, anche, per esempio, nei fenomeni d'urto. Basta ammettere che la probabilità al tempo t di trovare l'elettrone entro un elemento di volume dτ intorno al punto x sia uguale a ∣ ψ(x, t) ∣² dτ. L'equazione (27) esprime allora la legge di conservazione della probabilità totale. Questa può venir posta uguale all'unità (secondo le ordinarie convenzioni del calcolo delle probabilità) moltiplicando la ψ, ove ciò sia necessario, per una costante di proporzionalità. Si dice allora che la funzione ψ è ‛normalizzata'; si noti che le ψ precedentemente scartate in base alla condizione al contorno all'infinito non sono così normalizzabili, perché l'integrale è divergente; l'interpretazione statistica fornisce così una giustificazione ulteriore del procedimento seguito.

Il fatto che la ψ, e con essa la probabilità, sia diversa da zero simultaneamente in diversi punti dello spazio, significa che la posizione dell'elettrone a un dato istante non è ben definita; quando si dice, per esempio, che un pacchetto d'onde percorre una certa traiettoria, s'intende che questa è definita solo sino a un certo punto è che lo è tanto meglio quanto più il pacchetto può considerarsi piccolo rispetto ad altre dimensioni caratteristiche, come il diametro di un'orbita chiusa, il raggio di curvatura, ecc.

Naturalmente, nota la distribuzione di probabilità di una coordinata x, si può poi definire esattamente sia il valore probabile medio 〈x> a un dato istante, sia i ‛momenti superiori', cioe i valori medi 〈x²>, 〈x³>, ecc. Se ne deduce, per esempio, la deviazione quadratica media Δx, che misura l'incertezza statistica della posizione. Dopo di ciò è logico interpretare la funzione c(k) nell'eq. (26) come un'ampiezza di probabilità per l'impulso. Difatti, già in base alla concezione originaria di de Broglie, una singola onda piana deve rappresentare elettroni aventi un determinato impulso p = ℏk; una sovrapposizione di diverse onde piane può soltanto rappresentare uno stato di impulso mal definito; per di più si può mostrare che, se l'impulso viene misurato, la probabilità di trovare un certo valore di k = p/ℏ entro un elemento di volume (dk) deve esser proporzionale a ∣ c(k) ∣²(dk). L'eq. (26), valida per particelle libere, si può generalizzare, insieme alle considerazioni precedenti, al caso di una particella soggetta a un potenziale; le ampiezze c(k) dipendono allora anche dal tempo, com'è naturale quando l'impulso non è una ‛costante del moto'.

È un fatto elementare della teoria di Fourier, ben noto dall'ottica, che la larghezza spettrale Δν di un treno d'onde è inversamente proporzionale alla sua lunghezza; l'applicazione di questo principio alla (26) ci fa concludere che un pacchetto d'onde con una x molto ben definita (cioè una Δx molto piccola) deve avere una componente dell'impulso p_x molto poco definita. Più precisamente si prova la ‛relazione d'indeterminazione di Heisenberg':

Δx • Δp_x ≥ ½ℏ. (28)

In questa e in analoghe relazioni si può vedere l'origine della natura probabilistica delle previsioni della meccanica quantistica.

Alcuni autori ritengono che la descrizione della realtà fisica data dalla meccanica quantistica sia incompleta; vi sarebbero cioè ‛variabili nascoste' di cui la teoria non tiene conto; se queste potessero venir misurate, sarebbero nuovamente possibili previsioni di natura strettamente causale secondo il modello classico. È interessante osservare (v. Bell, 1964; v. anche Wigner, 1970) che la differenza fra quest'ipotesi e la meccanica quantistica è direttamente verificabile mediante opportune esperienze. Secondo la tesi svolta da Heisenberg e più ampiamente da Bohr, e oggi generalmente accettata, le relazioni d'indeterminazione rappresentano una limitazione intrinseca alla possibilità di misurare simultaneamente la posizione e la velocità di una particella; questa limitazione è una conseguenza diretta dell'esistenza del quanto d'azione, che determina il carattere individuale degli atti di interazione elementari su cui si basa in ultima analisi ogni misura.

e) Equazione e funzioni d'onda per un sistema di n corpi.

La concezione più vasta, di una meccanica ondulatoria applicabile a un sistema con un numero qualsiasi di gradi di libertà, fu suggerita a Schrödinger dall'antica analogia, di Hamilton, tra la meccanica e l'ottica geometrica. Nel caso più semplice questa non è altro che l'analogia tra il principio di Fermat dell'ottica geometrica per un mezzo a indice di rifrazione n(x, y, z) variabile in modo continuo e il principio di Maupertuis della minima azione per una particella in moto sotto l'azione di un potenziale conservativo V(x, y, z). Abbiamo già notato che secondo le leggi dell'ottica il numero d'onda k = 2π/λ varia da punto a punto proporzionalmente all'indice di rifrazione - purché, beninteso, la frequenza rimanga costante. Nel caso limite delle piccole lunghezze d'onda (quando gli effetti di diffrazione sono trascurabili) l'equazione d'onda dà risultati equivalenti a quelli dell'ottica geometrica, che costruisce le superfici d'onda come superfici ortogonali ai ‛raggi' di luce, che obbediscono al principio del minimo cammino ottico di Fermat. Per l'equazione d'onda (21), tenendo presente la legge n ∝ k, il cammino ottico è:

∫ n(x, y, z) ds ∝ ∫ {2m[E − V(x, y, z]}^1/2ds (29)

e coincide quindi con l'integrale d'azione della dinamica, che compare anche nella regola di quantizzazione (9). I ‛raggi' coincidono dunque con le traiettorie delle particelle. Questa è l'analogia di Hamilton nel caso più semplice, che si può estendere anche, per esempio, alla dinamica di un elettrone in campi elettrici e magnetici combinati. L'equazione di Schrödinger per questo caso è una generalizzazione della (22). Si può così mostrare che le classiche esperienze sui raggi catodici (misura di e/m, ecc.), presentate spesso come prove della natura corpuscolare di questi raggi, si possono interpretare altrettanto facilmente mediante l'equazione d'onda.

Hamilton stesso aveva esteso la sua analogia a un sistema conservativo con un numero qualsiasi f di gradi di libertà, con coordinate lagrangiane di posizione q₁, q₂, ..., q_f e momenti coniugati p₁, p₂, ..., p_f. L'analogo ottico è un'astratta ottica geometrica nello spazi o a f dimensioni. Questo indusse Schrödinger a formulare una corrispondente equazione d'onda nello stesso spazio, che si ottiene come segue. Sia H(q₁, ..., q_f; p_f; p₁, ... p_f) la funzione di Hamilton, che abbreviamo H(q; p). Nella dinamica classica questa funzione è una costante del moto e precisamente l'energia del sistema; da essa si deducono le equazioni del moto nel modo solito. Per ottenere l'equazione d'onda si consideri H(q; p) come un operatore differenziale, detto operatore hamiltoniano ottenuto con la sostituzione simbolica:

p_s → iℏ ῼ/ῼq_s (s = 1, 2, ... f), (30)

che agisce sulla funzione d'onda ψ(q₁, q₂, ..., q_f), abbreviata ψ(q).

L'equazione d'onda indipendente dal tempo, per esempio, è allora:

H(q; p)ψ(q) = Eψ(q). (31)

n elettroni (o più in generale n particelle) avranno f = 3n coordinate di posizione x₁, y₁, z₁, x₂, ..., x_n, z_n. Gli impulsi corrispondenti diventano gli operatori −iℏ ῼ/ῼx₁, ..., −iℏ ῼ/ῼz_n. Il termine che rappresenta l'energia cinetica in H(q; p) diventa allora:

Se vi è nell'origine un nucleo di carica Ze il termine ‛energia potenziale' è:

dove

r_i = (x2_i + y2_i + z2_i)^1/2, r_ij = [(x_i − x_j)² + ...]^1/2.

L'equazione (31) si può ora scrivere in modo conciso:

la (32) per n = 1 si riduce alla (21).

Il calcolo degli autovalori della (32) per n = 2, 3, ... è assai meno semplice che per l'atomo di idrogeno. Non esistono soluzioni esplicite; vi sono ciononostante approssimazioni estremamente accurate delle soluzioni, il cui accordo con le misure non lascia alcun dubbio sulla validità dell'equazione per i sistemi di più elettroni. Si tratta, beninteso, di validità entro il limite dell'approssimazione non relativistica. Le correzioni relativistiche, di cui si dirà più avanti, sono del resto estremamente piccole per gli elementi leggeri. L'eq. (32) si può facilmente generalizzare, com'è ovvio, in modo da includere particelle di massa diversa, per esempio il nucleo dell'atomo o i nuclei di una molecola. Si ha così una dinamica completa di questi sistemi, che permette di analizzare con grande ricchezza di risultati la struttura di rotazione e oscillazione dei livelli di una molecola e simili problemi. Ricordiamo infine che anche per i sistemi di più particelle la teoria descritta è completamente equivalente allo schema delle matrici di Born, Jordan e Heisenberg.

Anche concettualmente la (32) è assai importante. Essa ci fornisce uno dei migliori argomenti contro l'interpretazione della ψ come un campo classico. Non vi è nulla di classico in un'onda in uno spazio astratto a 3n dimensioni; viceversa l'interpretazione della ψ come un'ampiezza di probabilità si estende al caso degli n corpi senza alcuna difficoltà. Basta considerare l'espressione ∣ ψ(x₁, ..., x_n) ∣² dτ₁ dτ₂ ... dτ_n come la probabilità di trovare la prima particella entro l'elemento di volume dτ₁ intorno al punto x₁ e allo stesso tempo la seconda particella entro l'elemento dτ₂ intorno a x₂ e così via. La ψ può descrivere anche complicate correlazioni tra le posizioni di varie particelle e, in modo del tutto simile, correlazioni tra le velocità di diverse particelle, o tra le loro energie, ecc. Come ciò avvenga si può vedere dall'esempio seguente.

Funzioni d'onda per più elettroni nella forma di semplici prodotti di funzioni delle coordinate dei singoli elettroni possono essere considerate come soluzioni approssimate della (32) se si trascurano le interazioni a due a due tra gli elettroni (ma non quella col campo centrale). Per due elettroni si ponga, per esempio:

ψ(x₁, x₂) = u_a(x₁)u_b(x₂), (33)

dove u_a (rispettivamente u_b) è un'autofunzione per un singolo elettrone nel campo centrale, con energia E_a (rispettivamente Eb). L'autovalore dell'energia totale, in questa approssimazione, è E_a + E_b. Diremo che ψ rappresenta uno stato tale che l'elettrone i si trova nel livello E_a e il 2 nel livello E_b. Evidentemente possiamo scambiare i ruoli dei due elettroni senza alterare l'energia totale; è anche lecito combinare linearmente le due diverse autofunzioni così ottenute, per esempio:

ψ = u_a(x₁)u_b(x₂) − u_a(x₂)u_b(x₁). (34)

Si noti che questa è un'autofunzione (approssimata) dell'operatore energia totale, ma non dell'energia del primo (o del secondo) elettrone; ciò è possibile grazie alla correlazione esistente in questo stato tra le energie dei due elettroni. La possibilità di queste correlazioni nel formalismo ondulatorio generalizzato elimina interamente le contraddizioni incontrate inizialmente (v. cap. 2, È c) tra l'interpretazione statistica delle onde e le leggi di conservazione dell'energia e dell'impulso.

f) Momento angolare intrinseco (spin) dell'elettrone, principio di esclusione.

La funzione d'onda può anche venir generalizzata per tener conto dello spin dell'elettrone e del momento magnetico a esso associato, momento la cui esistenza fu dapprima intuita da Goudsmit e Uhlenbeck in base ai risultati delle ricerche sulla struttura fine delle righe spettrali e sull'effetto Zeeman anomalo. Il momento angolare intrinseco ha il più piccolo valore consentito dalla teoria e cioè ½ℏ (v. cap. 5, È c). Il grado di libertà corrispondente possiede così soltanto due stati linearmente indipendenti α e β (oppure spin all'insù e all'ingiù): esso si può descrivere mediante un'autofunzione (detta di Pauli) a due componenti. Nel caso di n elettroni, l'autofunzio nella 2ⁿ componenti, poiché ogni elettrone può avere indipendentemente due diversi stati dello spin.

La meccanica quantistica ci offre a questo punto una piacevole sorpresa, nella facilità con cui essa può assimimilare il principio di esclusione, formulato anteriormente da Pauli su basi strettamente sperimentali. Nella sua forma originaria, il principio afferma che due elettroni non possono avere esattamente gli stessi numeri quantici (bisogna tener conto anche del numero quantico dello spin, che può assumere due valori). Nell'antica teoria quantica questo principio, che ha basi sperimentali assai solide, è difficile da comprendere. La forma esatta del principio nella meccanica ondulatoria è la seguente: una funzione d'onda per n elettroni deve essere totalmente antisimmetrica, ossia deve cambiar segno se si scambiano le coordinate cartesiane e di spin di una qualsiasi coppia di elettroni. Questa è una condizione di simmetria la quale (v. cap. 5, È b) commuta con l'operatore di Hamilton ed è quindi perfettamente compatibile con l'equazione di Schrödinger. Omettendo lo spin, abbiamo nella (34) l'esempio più semplice di una funzione antisimmetrica (la stessa formula con un segno + ci darebbe una funzione simmetrica). Notiamo subito che, se nella (34) si pone a = b, la funzione si annulla identicamente: nello stato anti simmetrico i due elettroni non possono avere gli stessi numeri quantici. Proseguendo per questa via si può mostrare che la forma esatta del principio contiene in sé, oltre a nuove importanti conseguenze, anche tutte quelle della forma più antica, come la nozione di anelli elettronici chiusi (importantissima nell'interpretazione del sistema periodico degli elementi; v. atomo), la validità della statistica di Fermi per il gas di elettroni liberi in un metallo e così via. Il principio di esclusione, nella sua forma esatta, si estende ad altri sistemi di particelle identiche (per esempio sistemi di protoni, di neutroni, ecc.).

Con lo spin e col principio di esclusione abbiamo completato in sostanza il quadro della meccanica quantistica non relativistica, la quale ci fornisce secondo l'opinione corrente - un insieme di leggi fondamentali sufficienti (a parte le difficoltà matematiche che si possono presentare nel caso di sistemi molto complicati) per una discussione quantitativa del comportamento della materia in condizioni ordinarie. Questa opinione si basa sul fatto che la teoria suddetta è stata applicata con grande successo non solo allo studio delle proprietà individuali di atomi o molecole, ma anche a sistemi più complicati, come i cristalli o i liquidi. Per lo studio di certi particolari degli spettri degli atomi e delle molecole, come la struttura fine dello spettro ottico o dei raggi X, o la struttura iperfine, occorre tener conto, nell'operatore hamiltoniano, di certi termini, come l'interazione ‛spin-orbita', che a dire il vero rappresentano correzioni relativistiche, ma a causa della loro estrema piccolezza possono in genere venir calcolati come piccole perturbazioni a partire dalle funzioni d'onda non relativistiche.

Nel caso delle molecole la meccanica quantistica ci ha dato un'idea qualitativa assai più chiara, e in certi casi un calcolo quantitativo, del legame chimico nelle molecole e della valenza, grazie agli studi avviati dal classico lavoro di Heitler e London sul legame omopolare nella molecola di idrogeno. L'applicazione della meccanica quantistica alla teoria dei metalli a partire dal 1928 (Bloch) ha portato a un completo rinnovamento della teoria della conduzione e del ferromagnetismo (Heisenberg). Il paramagnetismo alle basse temperature, la semiconduzione e, più recentemente, la superfluidità e la superconduzione sono altri fenomeni alla cui comprensione la meccanica quantistica ha contribuito in modo essenziale.

4. Principi generali della meccanica quantistica.

a) Vettori di stato, operatori hermitiani

Si possono individuare nel formalismo di Schrödinger alcuni principi che costituiscono lo scheletro di una teoria più generale. Si capisce così perché siano possibili diverse forme della teoria (teoria delle trasformazioni).

Le funzioni d'onda che descrivono gli stati di un sistema possono venir concepite come ‛vettori' (cioè come elementi di uno ‛spazio vettoriale') in senso astratto. Questo è naturale, poiché le regole fondamentali di uno spazio vettoriale sono le regole di sovrapposizione (o combinazione) lineare, regole identiche a quelle su cui si fonda l'interpretazione ondulatorio-probabilistica dei fenomeni di interferenza e diffrazione. Più precisamente, abbiamo a che fare con uno spazio vettoriale a coefficienti complessi. Tutto ciò sarà riassunto più avanti nel postulato generale A.

Esaminando la (27) ed espressioni analoghe in altri casi si giunge alla conclusione che la ‛probabilità totale' è data in generale da una forma quadratica, definita positiva, nel ‛vettore di stato' (funzione d'onda) ψ, forma che indicheremo con il ∥ψ∥² Spazi vettoriali dotati di una siffatta forma quadratica (che per definizione è invariante rispetto ai cambiamenti di coordinate) si chiamano spazi di Hilbert. Questo requisito verrà dunque aggiunto espressamente. Dalla forma quadratica si deduce con semplici operazioni il concetto derivato di ‛prodotto scalare hermitiano' di due vettori ψ₁ e ψ₂ designato con (ψ₁, ψ₂), che ha un ruolo importante nel calcolo delle probabilità (v. sotto il postulato C). Nel caso specifico della (27), per esempio, il prodotto scalare è.

(ψ₁, ψ₂) = ∫ ψ₁*(x, t)ψ₂(x, t) dτ. (35)

Si può mostrare che, come la (27), anche questa espressione è indipendente dal tempo t, purché ψ₁ e ψ₂ siano soluzioni della (22). In modo del tutto generale il prodotto scalare (ψ₁, ψ₂) è lineare in ψ₂ e antilineare in ψ₁ (cioè, se in luogo di ψ₁ compare cψ₁, allora il prodotto scalare si moltiplica per la costante complessa coniugata c*); se si pone ψ₁ = ψ₂ = ψ, il prodotto scalare diventa la forma quadratica di partenza ∥ ψ ∥².

Gli operatori di impulso dell'eq. (30) e l'operatore di Hamilton H(q; p) dell'eq. (31) sono esempi di ‛operatori lineari hermitiani' che agiscono sui vettori ψ dando altri vettori dello spazio di Hilbert. L'affermazione ‟Ω è un operatore lineare" significa: Ω(ψ₁ + ψ₂) = Ωψ₁ + Ωψ₂ e inoltre Ω(cψ) = cΩψ, se c è una qualsiasi costante complessa. L'aggettivo ‛hermitiano' significa che il prodotto scalare (ψ, Ωψ) è sempre reale. Un autovalore dell'operatore Ω è una costante λ tale che l'equazione

Ωψ = λψ (36)

possegga una o più soluzioni ψ non nulle ('autovettori'); si tratta di ovvie generalizzazioni dell'idea di autofunzione. Il postulato B, che diamo più avanti, è una generalizzazione naturale della condizione di Schrödinger per i livelli energetici e di altri esempi, che qui non citiamo. Si dimostra che gli autovalori di un operatore hermitiano sono necessariamente reali; donde l'importanza di questi operatori per la rappresentazione delle grandezze fisiche.

Altre importanti proprietà di un operatore hermitiano sono il teorema di ortogonalità, che asserisce che due autovettori ψ₁, ψ₂, corrispondenti ad autovalori distinti (λ₁ ≠ λ₂), sono tra loro ortogonali, cioè che risulta (ψ₁, ψ₂) = 0, e un teorema di sviluppo che viene usato per giustificare formule come la (25). Quest'ultimo teorema, che vale per ampie classi di operatori Ω e, sia pure in forma lievemente diversa, anche nel caso di uno spettro continuo di autovalori, afferma che Ω possiede una ‛base' di autovettori ψ₁, ψ₂, ..., ossia un insieme di autovettori tale che qualsiasi vettore si può sviluppare, in uno e in un solo modo, in una serie del tipo Σ c_nψ_n; tale base si può inoltre supporre ‛ortonormale', cioè consistente di vettori normalizzati a due a due ortogonali. Poiché sarebbe ovviamente assurdo, in generale, interpretare lo stato descritto dalla (25) come uno stato di energia ben determinata, dobbiamo supporre che l'interpretazione statistica della ψ si estenda anche alle misure di energia; è allora naturale considerare la c_n nella (25) come un'ampiezza di probabilità per il livello energetico E_n; la corrispondente probabilità deve essere proporzionale a ∣ c_n ∣². Come conseguenza del postulato B, queste considerazioni vengono estese ad altre grandezze fisiche nel postulato C, che ora enunceremo insieme agli altri due.

A. Gli stati di un sistema sono rappresentati da vettori in uno spazio di Hilbert. Lo stato non cambia se il vettore ψ viene cambiato in cψ, dove c è una costante complessa. Un dettaglio tecnico, non secondario, è il seguente: una funzione d'onda è elemento di uno spazio di Hilbert solo se l'integrale che definisce la probabilità totale è finito; in tal caso essa può ovviamente venir nomalizzata, se ciò è necessario, moltiplicandola per una costante finita c, tale che ∥ ψ ∥² diventi eguale all'unità (ciò che corrisponde all'usuale convenzione nel calcolo delle probabilità).

B. Le grandezze fisiche reali sono rappresentate da operatori lineari (hermitiani) nello spazio di Hilbert. I valori numerici possibili di una grandezza fisica sono gli autovalori λ₁, λ₂, ... del corrispondente operatore. Gli autovettori associati ψ₁, ψ₂, ... (preferibilmente normalizzati) rappresentano stati in cui la grandezza detta è ben definita. Una notazione un po' diversa è necessaria (v. Dirac, 1930) nel caso di uno spettro continuo di autovalori, che richiede anche condizioni di normalizzazione diverse su cui non ci dilunghiamo; la notazione usata presuppone inoltre, per semplicità, che gli autovalori λ_n non siano degeneri.

C. Se lo stato del sistema è rappresentato dal vettore normalizzato

(dove le ψ_n sono normalizzate), i possibili risultati λ₁, ..., λ_n, ... di una misura della grandezza Ω hanno le probabilità p₁, ..., p_n, ..., date da

p_n = ∣ c_n ∣² = ∣ (ψ_n, ψ) ∣². (37)

Quest'ultima affermazione si fonda sulle seguenti identità (di facile dimostrazione):

Tutte le probabilità p_n rimangono invariate se la ψ si moltiplica per un fattore di fase c = e^iα (α reale), il che si accorda con quanto si è in A

b) Algebra degli operatori, commutatori.

Gli operatori in uno spazio di Hilbert sono elementi di un'algebra: possono essere moltiplicati per una costante arbitraria e possono essere sommati o moltiplicati fra di loro. Le regole di quest'algebra si possono anche ricavare in modo quasi automatico dalla convenzione di scrivere un'operatore Ω sempre dalla stessa parte (per esempio a sinistra) del vettore su cui l'operatore agisce: Ωψ. Quest'algebra ha un ‛elemento unità': l'operatore ‛identità' 1, definito dalla 1 ψ = ψ. Gli operatori che rappresentano le coordinate q_s e gli impulsi p_s (v. la 130) agiscono sulla ψ(q) nel modo che segue: q_s[ψ(q)] = q_sψ(q)] = − ihῼψ/ῼq_s. Il prodotto AB di due operatori è definito dalla: (AB)ψ = A(Bψ). A parole: dapprima B agisce sulla ψ, poi A agisce sul risultato. In generale AB ≠ BA (non commutatività del prodotto di due operatori). L'esempio classico è:

D'altra parte q_s e p_s, (dove s ≠ s′) commutano. Tutto ciò è riassunto dall'equazione tra operatori

q_sp_s′ − p_s′q_s = iℏ δ_ss′1, (39)

dove δ_ss′ è il simbolo di Kronecker (=1, se s = s′, = 0 altrimenti). Questa celeberrima equazione compare anche nella meccanica di Heisenberg come relazione fra matrici. Come ha mostrato Dirac, il commutatore [A, B] di due operatori, definito dalla

[A, B] = AB − BA, (40)

diviso per iℏ, rappresenta l'analogo quantistico delle parentesi di Poisson, di modo che le (39) corrispondono a relazioni ben note nella dinamica classica. D'altra parte esse sono connesse direttamente con il principio di indeterminazione di Heisenberg. Qualitativamente la connessione è la seguente: uno stato in cui le due grandezze sono entrambe ben definite deve corrispondere a una ψ, che è simultaneamente un autovettore sia di A che di B, con autovalori, diciamo, a e b. Ne segue facilmente che ABψ = A(bψ) = bAψ = baψ = ... = BAψ,. Ma la (39) ci dice precisamente che per A = q_s, B = p_s (con lo stesso indice) un siffatto vettore non può esistere. Più in generale, se [A, B] ≠ 0, devono esistere dei vettori sui quali AB e BA agiscono in modo diverso. Ciò rappresenta necessariamente una restrizione della possibilità di determinare le due grandezze simultaneamente.

c) Teoria delle trasformazioni.

Un vettore dello spazio di Hilbert può venire definito semplicemente come una serie di coefficienti:

(c₁ , c₂, c₃, ..., c_n, ...). (41)

S'intende che le c_n sono le componenti dello sviluppo ψ = Σ_nc_nψ_n del vettore ψ relativamente a una base ortonormale di vettori. Spesso la (41) viene scritta come una matrice (infinita) a una colonna, anziché a una riga. La (38) serve allora da definizione della norma del vettore. Un operatore A può venire similmente definito mediante una doppia successione di coefficienti A_ij, gli ‛elementi di matrice'. Infatti, essendo A lineare, la sua azione su un qualsiasi vettore, A(Σ_jc_jψ_j) = Σ_jc_jAψ_j, sarà nota, ove Aψ_j sia noto per j = 1, 2, ... Ma, poiché ψ₁, ψ₂, ... e una base, si deve avere Aψ_j = Σ_jA_ijψ_i, dove le A_ij sono coefficienti numerici, che definiscono dunque l'operatore. Si verifica facilmente che la matrice che rappresenta il prodotto AR si ottiene con la regola del prodotto di matrici: (AB)_ij = Σ_nA_inB_nj. Così prùcedendo, e mediante la (39), si dimostra facilmente l'equivalenza dello schema ondulatorio con la meccanica delle matrici.

La teoria delle trasformazioni nasce dal fatto che nello spazio dei vettori di stato è possibile, e spesso desiderabile, passare a un nuovo insieme base di vettori ψ1′, ψ2′, ... Poiché ψj′ si può esprimere come una combinazione lineare

dei vettori di base originari (e viceversa), si può scrivere simbolicamente

ψj′ = Uψ_j; ψ_j = U^-1ψj′, (43)

dove U e U^-1 sono operatori tali che UU^-1 = U^-1U = 1. Se entrambe le basi sono ortonormali, si provano facilmente le relazioni

Si dice allora che l'operatore U è ‛unitario'.

In pratica è importante, nelle applicazioni fisiche, il fatto che i vettori base siano di solito definiti non già come autovettori di un singolo operatore (come H, per es.) bensì come autovettori simultanei di un insieme di operatori che commutano tra di loro. Così nel problema dell'idrogeno le autofunzioni hanno come indici tre numeri quantici, che identificano gli autovalori rispettivamente dell'energia, del momento angolare totale e di una componente dello stesso lungo una qualche direzione fissa. Questi autovalori simultanei sono possibili perché gli operatori corrispondenti commutano.

La teoria delle trasformazioni è utile, perché ci permette di scegliere gli stati base nel modo più adatto alla questione prescelta. Altri utili insiemi base sono, per esempio, gli autovettori di posizione o, rispettivamente, di impulso; in ambo i casi abbiamo a che fare con indici variabili in modo continuo, argomento a cui abbiamo appena accennato. Ma le componenti del vettore ψ rispetto a queste basi non sono altro che la funzione ψ(q) e, rispettivamente, la sua trasformata di Fourier c(k) dell'eq. (26). Quest'ul tima è, beninteso, un caso speciale (per una singola particella libera). Una particolare scelta della base viene anche chiamata ‛rappresentazione' (per esempio ‛rappresentazione degli impulsi', ecc.).

d) Rappresentazione di Heisenberg.

Una questione analoga si presenta nella distinzione tra ‛rappresentazione di Heisenberg' e ‛di Schrödinger', di cui approfittiamo per chiarire un'ambiguità semantica, che abbiamo sinora deliberatamente ignorato, nell'uso della frase ‛stato di un sistema' (v., per esempio, i postulati A, B, C). La frase viene usata nel senso di ‛stato a un certo istante t', nel qual caso lo stato, in generale, varierà col tempo e così dovrà variare il vettore che lo rappresenta. L'equazione ‛temporale' di Schrödinger (più generalmente iℏ ῼψ/ῼt = Hψ descrive appunto il modo in cui il vettore ‛ varia col tempo. In altre parole, lo spazio di Hilbert viene concepito come lo spazio delle funzioni ψ(q) e la funzione d'onda ψ(q; t) viene pensata come una famiglia di funzioni ψ(q), mentre il tempo funziona da ‛indice' entro la famiglia. Questa è la rappresentazione di Schrödinger, nella quale gli operatori che rappresentano le coordinate, gli impulsi e le altre grandezze fisiche non dipendono dal tempo esplicitamente. Il variare col tempo del valore di queste grandezze, o più precisamente il variare delle probabilità dei loro valori, è descritto in questa rappresentazione dal variare della ip, nell'eq. (37) per esempio. Allo stesso modo varia il ‛probabile valor medio' di una grandezza Ω, che secondo le regole del calcolo delle probabilità è definito come 〈Ω> = Σ_np_nλ_n. Mediante la (37) si vede facilmente che

〈Ω> = (ψ, Ωψ) (45)

varia col tempo insieme con la ψ.

Nella ‛rappresentazione di Heisenberg' il vettore di stato è indipendente dal tempo. Ciò corrisponde all'idea di stato, come si suol dire sub specie aeternitatis (l'analogo classico è ‛una certa soluzione delle equazioni del moto' e non ‛l'insieme delle posizioni e delle velocità delle varie parti del sistema a un dato istante'). Per esempio, le costanti c_n della (25) definiscono, nel senso della (41), il ‛vettore di stato di Heisenberg'. Spetta ora agli operatori il compito di descrivere la dipendenza dal tempo, per esempio del probabile valor medio. Se ne deduce una dipendenza dal tempo descritta dall'equazione del moto di Heisenberg

la quale, grazie alla suddetta analogia tra commutatori e parentesi di Poisson, presenta la più stretta somiglianza con le equazioni di Hamilton della dinamica classica. Inoltre, in questa rappresentazione, le ‛costanti del moto' sono, come nella dinamica classica, le quantità la cui derivata rispetto al tempo si annulla. Ne segue l'importante regola: ‛i corrispondenti operatori commutano con l'operatore energia'.

5. Simmetrie o principi di invarianza nella meccanica quantistica.

a) Gruppi di trasformazioni delle coordinate.

Le considerazioni di simmetria e la loro classica relazione con le leggi di conservazione assumono nella meccanica quantistica una forma particolarmente significativa. Consideriamo l'esempio dell'invarianza rispetto al gruppo di trasformazioni dell'ordinario spazio euclideo, gruppo che è generato dalle traslazioni e dalle rotazioni del sistema cartesiano di riferimento. Le corrispondenti trasformazioni delle coordinate e le trasformazioni inverse si possono scrivere come

x′ = x + α; x = x′ − α, (47)

dove α è un vettore costante arbitrario, e rispettivamente

x′ = ax; x = a^-1x′, (48)

dove a è una trasformazione ortogonale il cui determinante è +1. Consideriamo per semplicità un sistema di n particelle non relativistiche, che interagiscono a due a due mediante potenziali V_ij che dipendono solo dalla distanza r_ij = ∣ x_i − x_j ∣. Supponiamo che non vi sia alcun campo esterno; queste considerazioni si applicheranno anche a un atomo (o a una molecola) se il nucleo viene anch'esso considerato come una particella mobile di massa finita (se il nucleo di un atomo viene supposto fisso nell'origine delle coordinate, si ha ancora invarianza rispetto alle rotazioni, con tutte le conseguenze che ciò comporta, ma evidentemente non rispetto alle traslazioni). Si prevede allora, e si verifica facilmente, l'invarianza dell'equazione di Schrödinger rispetto alle trasformazioni (47) e (48). Più esplicitamente: si scriva la (32) per la funzione d'onda ψ(x₁, ..., x_n) e si trasformi poi la ψ esprimendo le variabili x₁,... (di cui essa è funzione) come funzioni delle coordinate con apice. Il risultato è una diversa funzione ψ′ delle variabili x1′, ... ecc., vale a dire

ψ′ (x1′, ..., xn′) = ψ(x1′ − α, ..., xn′ − α) (49)

o rispettivamente

ψ′ (x1′, ..., xn′) = ψ(α^-1 x1′, ..., a^-1 xn′). (50)

L'equazione soddisfatta dalla ψ′ nelle nuove coordinate ha esattamente la stessa forma (32). Questo è il principio di invarianza. Se non conoscessimo la forma esatta della legge di interazione o quella dell'equazione d'onda, potremmo usare il principio come un requisito che le possibili interazioni devono soddisfare. Vediamo ora come da tale principio si possano anche dedurre le leggi di conservazione.

b) Trasformazioni unitarie della funzione d'onda, leggi di conservazione.

Le eqq. (49) e (50) possono considerarsi come trasformazioni unitarie delle componenti del vettore ψ alla stessa stregua di quelle considerate nel cap. 4, È c, a parte la circostanza già notata che le componenti che qui occorrono hanno indici continui. Un modo leggermente diverso di considerare le cose è il seguente. Il dominio dei valori possibili delle coordinate x1′... è esattamente lo stesso delle x₁, ... (si noti che il ragionamento varrebbe anche se si trattasse di altre grandezze fisiche qualsiasi, purché si trattasse di grandezze ‛analoghe' rispetto ai due sistemi equivalenti). Si possono quindi omettere gli apici, scrivendo la (49), per esempio,

ψ′ (x₁, x₂, ..., x_n) = ψ(x₁ − α, ..., x_n − α), (51)

ovvero ψ′ = Uψ, dove U è un operatore che trasforma ψ in un nuovo vettore ψ′. Questo principio è del tutto generale e si può usare ogniqualvolta si ha a che fare con sistemi di riferimento equivalenti. Si vede facilmente che U è lineare e unitario.

Ammessa l'esistenza di due sistemi di riferimento equivalenti, allora anche quella dell'operatore U, cioè di una trasformazione della funzione d'onda, si deve ammettere a priori per ragioni d'ordine generale; si noti che, se non esiste una specifica connessione tra le funzioni d'onda nei due sistemi, l'affermazione che l'equazione di Schrödinger ha la stessa forma nei due casi è priva di significato.

L'equazione d'onda Hψ = Eψ si trasforma nell'equazione HU^-1ψ′ = EU^-1ψ′ per la ψ′ e poi nella UHU^-1ψ′ = Eψ′, moltiplicando per U a sinistra. Poiché questa deve essere la stessa equazione valida per la ψ, si deve avere UHU^-1 = H o, ciò che fa lo stesso,

UH = HU. (52)

L'operatore U di trasfomazione della ψ deve dunque commutare con H e rappresenta perciò una ‛costante del moto'. Questa è la relazione fondamentale tra invarianza e leggi di conservazione. Essa diventa ancora più chiara se si considerano trasformazioni infinitesime. Se per esempio nella (51) la traslazione è nella direzione dell'asse x, α = (ε, 0, 0), ed è infinitesima, allora si può porre

trascurando i termini in ε². Ciò corrisponde a

U = 1 − i(ε/ℏ)P_x, (53)

dove

è l'operatore che rappresenta la componente x della quantità di moto totale. Analogamente, se consideriamo una rotazione di angolo infinitesimo ϑ, per esempio intorno all'asse z, si avrà a^-1x = (x + ϑy - y − ϑx, z) e quindi

trascurando ϑ². Questa volta scriveremo

U = 1 − i(ϑ/ℏ)M_z, (54)

dove

(p_kx = − iℏ ῼ/ῼx_k, ..., ecc.); nella (55) riconosciamo l'analogo dell'espressione classica per la componente z del momento angolare totale. Grazie alla (53) e alla (54) le componenti di P e di M si chiamano ‛generatori' infinitesimali (di traslazioni e rotazioni, rispettivamente). Poiché l'identità i commuta con qualsiasi operatore, la (52) diventa ora

[H, P_x] = 0 o, rispettivamente, [H, M_z] = 0. (56)

Mediante considerazioni di invarianza abbiamo cosi recuperato due classiche leggi di conservazione: quella della quantità di moto e quella del momento angolare.

È opportuno osservare che le relazioni (52) per le trasformazioni finite non hanno un analogo classico utile. È una proprietà particolare della meccanica quantistica il fatto che anche le simmetrie discrete generino costanti del moto. Il numero quantico di parità ne è un esempio (v. più avanti). Un altro esempio importante è costituito dalle ‛permutazioni di particelle identiche' (v. Dirac, 1930; v. van der Waerden, 1931; v. Wigner, 1959). Lo scambio P_ij delle coordinate delle particelle i e j nella soluzione ψ dell'equazione d'onda si può considerare come un operatore lineare che commuta con H (cioè non modifica l'equazione) se le particelle sono uguali. Quindi P_ij è una costante del moto, senza analogo classico. Poiché P2_ij = 1, i suoi soli autovalori possibili sono 1 e −1. Dire che P_ij = −1 significa che l'autofunzione è antisimmetrica nelle due particelle. Di qui si passa facilmente al ‛principio di esclusione'.

c) Rappresentazioni, algebra di Lie.

La composizione di due trasformazioni viene di solito descritta come un prodotto (v. l'analoga convenzione per gli operatori>, il quale è associativo, cioè (ab)c = a(bc), ma non necessariamente commutativo, cioè in generale ab ≠ ba. Se indichiamo con a, b, ... elementi (cioè trasformazioni) del gruppo euclideo e con U(a), U(b),... i corrispondenti operatori unitari sui vettori ψ, definiti precedentemente, è facile verificare che per due traslazioni o due rotazioni si ha

U(ab) = U(a)U(b). (57)

La validità di questa equazione si può estendere facilmente all'intero gruppo. Si dice allora che la corrispondenza a → U(a) è una ‛rappresentazione' del gruppo (mediante operatori in uno spazio di Hilbert). Analogamente, quando le U(a) sono matrici n × n che soddisfano la (57), si parla di una rappresentazione a n dimensioni.

Dal fatto che due traslazioni commutano sempre si deduce che

[P_x, P_y] = 0, ecc. (58)

Le rotazioni, invece, in generale non commutano, nè tra di loro nè con le traslazioni. Considerando l'espressione U(a)U(b)U(a^-1)U(b^-1), dove a e b sono trasformazioni infinitesime, si deducono, dopo alcuni calcoli, le relazioni

[M_x, M_y] = iℏM_z, ecc., (59)

[M_x, P_y] = − [M_y, P_x] = iℏP_z, ecc., (60)

[M_x, P_x] = 0, ecc., (61)

nelle quali l'‛ecc.' indica relazioni ottenute con la sostituzione ciclicà x → y → z → x. Tutte queste relazioni si potrebbero dedurre in modo più elementare, per calcolo diretto, dalla (55). Il metodo gruppale è però assai più potente, in quanto il risultato vale senz'altro per strutture molto più complicate (per es., per una teoria di campo relativistica). Le equazioni (59), (60), (61), che esprimono i commutatori di due generatori come multipli (in altri casi, più generalmente, come combinazioni lineari) di altri generatori, definiscono l'‛algebra di Lie' del gruppo.

Le (59) sono ben note. È da esse che si deduce il fatto che i possibili autovalori dell'operatore M2_x + M2_y + M2_z (il quadrato del modulo del vettore momento angolare totale) sono della forma ℏ²J(J + 1), dove J è un numero intero, 0, 1, 2, ..., oppure semintero, 1/2, 3/2,... Simultaneamente una componente, M_z per esempio, può avere solo gli autovalori J, J − 1, ..., − J moltiplicati per ℏ. Questa è precisamente la quantizzazione del momento angolare, dedotta senza alcuna ipotesi particolare.

Come applicazione indichiamo il formalismo mediante il quale si descrive lo spin dell'elettrone. La più semplice rappresentazione non nulla dell'algebra di Lie (59) del gruppo delle rotazioni è data da matrici 2 × 2, M_x → ½ℏσ_x, ecc., dove le ‛matrici di Pauli' σ_x, σ_y, σ_z sono definite come segue:

Altre forme di queste matrici, considerate equivalenti, si possono ottenere mediante trasformazioni del tipo σ → 116u^-1, dove u è una matrice unitaria 2 × 2. Le matrici di Pauli agiscono su vettori a due componenti c₁, c₂ disposte sovente in una matrice di una sola colonna,

vi sono cioè soltanto due vettori linearmente indipendenti. Come vettori della base possiamo scegliere, per esempio,

Questi sono autovettori di σ_z: σ_zα = α, σ_zβ = − β; si tratta dunque di stati per i quali la componente z del momento angolare rappresentato dalle matrici (62) è ben definita e di fatto uguale a ½ℏ. Un elettrone o un protone nello stato di riposo (più generalmente qualsiasi particella di spin ½) può venire così descritto da una rappresentazione di questo tipo.

d) Parità.

La trasformazione x′ = − x (inversione spaziale) non è stata sinora inclusa nel gruppo. Sino al 1957 si riteneva che tutte le leggi naturali possedessero questa simmetria. Qualora (come spesso avviene) si possano trascurare le violazioni di questo principio, si può ammettere che esista un operatore unitario, spesso designato con P (l'operatore di parità), che commuta con H e trasforma la ψ in ψ′ = Pψ. Questo operatore è allora una ‛costante del moto', che non ha analogo classico. Si dimostra che gli autovettori di P si possono suddividere in due classi, i cosiddetti stati ‛pari' e ‛dispari'. Questa distinzione ha un ruolo importante nella spettroscopia, nella fisica delle particelle elementari, ecc.

e) Formule di intensitò, regole di selezione.

La maggior parte delle transizioni ottiche osservate sono transizioni di dipolo e la loro intensità è propozionale al quadrato degli elementi di matrice del momento elettrico di dipolo dell'atomo. La distribuzione di intensità tra le componenti di struttura fine di una riga spettrale, o nell'effetto Zeeman, presenta notevoli regolarità, secondo leggi aritmetiche precise e piuttosto semplici; a leggi consimili obbediscono anche le transizioni (importanti nella fisica nucleare) di quadrupolo o dipolo magnetico, ecc. Tutte queste leggi si possono dedurre (v. Condon e Shortley, 1935) mediante considerazioni di simmetria, per esempio dalle leggi di commutazione, cui obbediscono le tre componenti del dipolo, del tutto simili a quelle per P_x ecc. nelle (60) e (61). In particolare da considerazioni siffatte si deduce che gli elementi di matrice di dipolo si annullano (la transizione è ‛proibita') se non sono soddisfatte certe ‛regole di selezione'. La più nota di queste regole asserisce che la differenza J′ − J = ΔJ tra i numeri quantici del momento angolare totale dello stato finale e di quello iniziale deve soddisfare la condizione

ΔJ = ± 1 oppure 0 (64)

per una transizione di dipolo. Inoltre il caso J = J′ è anche proibito. Un'altra regola (di Laporte) dice che le parità dei due stati devono essere opposte. Fu questa regola ad attirare l'attenzione sull'importanza dell'inversione per le regole di selezione in genere.

6. Formulazione relativistica.

a) Operatori di simmetria del gruppo di Lorentz inomogeneo.

Il primo grande passo verso una formulazione relativistica della meccanica quantistica fu compiuto da Dirac nel 1927-1928. In base a un ragionamento geniale, seppure oggi discutibile, Dirac giunse alla sua celebre equazione, che ha dominato sino a oggi l'intero sviluppo dell'elettrodinamica quantistica.

I principî generali della meccanica quantistica sono formalmente compatibili con l'invarianza relativistica. L'equazione di Dirac ne è un esempio. Per veder ciò in modo più generale è preferibile adottare la rappresentazione di Heisenberg, nella quale un vettore ψ rappresenta uno stato indipendentemente dal tempo. È opportuno osservare che, non avendo il tempo un significato assoluto nella relatività, l'idea di ‛stato al tempo t' non ha un carattere relativistico e porta in certi casi a complicazioni formali. Le trasformazioni di coordinate della relatività ristretta possono allora venir discusse allo stesso modo di quelle trattate precedentemente. Si può di nuovo concludere che ad ogni siffatta trasformazione deve corrispondere un operatore unitario, che descrive la trasformazione del vettore di stato. L'unitarietà è richiesta dall'interpretazione probabilistica del prodotto scalare (v. eq. 37), che non deve dipendere dal sistema di riferimento; fanno eccezione le trasformazioni che scambiano il passato con il futuro, per le quali Wigner ha dimostrato che U è unitario ma antilineare o, come si dice concisamente, è antiunitario. È stato dimostrato (v. Wigner, 1939), sotto ipotesi assai generali, che questi operatori devono costituire una rappresentazione del gruppo di Lorentz inomogeneo, cioè devono obbedire (salvo una lieve complicazione che qui non discutiamo) alla relazione (57). Ne segue che qualsiasi schema relativistico deve possedere 10 generatori infinitesimali linearmente indipendenti, 4 dei quali sono le componenti P_x, P_y, P_z della quantità di moto totale e l'energia totale H (che è la ‛quarta componente' del vettore energia-impulso). I 6 generatori rimanenti sono le già note componenti M_x, ecc., che generano rotazioni, e K_x, ecc., che generano semplici trasformazioni di Lorentz nelle direzioni x, y, z rispettivamente. Insieme i 6 generatori costituiscono un esavettore (M, K). Le relazioni dell'algebra di Lie del gruppo sono ovvie estensioni delle relazioni (56), (58)-(61).

b) L'equazione di Dirac.

Così come esiste una rappresentazione bidimensionale del gruppo delle rotazioni ottenuta dalle matrici di Pauli dell'eq. (62), ponendo M_x = ½ℏα_x, allo stesso modo si possono generare con le stesse matrici due rappresentazioni distinte del gruppo di Lorentz omogeneo, generato dalle componenti dell'esavettore (M, K). Si ponga infatti K_x = ½ℏα_x, ecc. Le relazioni dell'algebra di Lie del gruppo sono allora, oltre a quelle già scritte, le seguenti:

[σ_x, α_y] = − [σ_y, α_x] = iα_z

[α_x, α_y] = 2iσ_z, ... (65)

È ovvio che queste relazioni si possono soddisfare ponendo α_x = σ_x, ecc., oppure α_x = − σ_x, ecc. (seconda soluzione). Queste due rappresentazioni si possono combinare insieme in una sola rappresentazione mediante matrici 4×4, introducendo vettori u (spinori di Dirac) a quattro componenti u₁, u₂, u₈, u₄, di cui le prime due si trasformano secondo la prima rappresentazione e le ultime due secondo l'altra. In questo spazio a 4 dimensioni si può ora introdurre anche una trasformazione (ossia una matrice 4×4) β che rappresenta l'inversione spaziale x′ = −x. Poiché questa trasformazione coincide con la sua inversa, si deve anche avere β = β^-1. Essa si compone inoltre in modo ben determinato con le altre trasformazioni del gruppo, per esempio commuta con le rotazioni e, viceversa, si deve avere βα_xβ^-1 = − a_x (ciò significa semplicemente che la velocità relativa di due sistemi inerziali cambia segno se si applica un inversione). Si vede infine che l'unica trasformazione che verifica tutte queste condizioni consiste semplicemente nello scambio delle prime due componenti del vettore u con le ultime due componenti. Esprimendo in modo ovvio le matrici 4×4 come matrici 2×2, i cui elementi sono a loro volta matrici 2×2, possiamo riassumere quanto si è detto nelle formule:

Valgono ancora le (65), salvo una lieve confusione di notazione, poiché le σ non sono più le matrici di Pauli, ma matrici 4×4 che si ottengono dalle α (v. eq. 66) omettendo il segno ‛−'. Le quattro matrici β, α_x, ... soddisfano le note relazioni di anticommutazione di Dirac (βα_x + α_xβ = 0, α_xα_y + α_yα_x = 0, ecc.; inoltre β² = α2_x = ... = 1). La funzione d'onda di Dirac è uno ‛spinore', le cui 4 componenti ψ₁, ..., ψ₄ sono funzioni di x, y, z, t. Le matrici α e β agiscono sulla ψ come sui vettori u già detti. Per elettroni liberi l'equazione di Dirac si scrive simbolicamente iℏ ῼψ/ῼt = Hψ, dove l'operatore H è

H = c(α p + m₀cβ) = c(α_xp_x + α_yp_z + α_zp_z + m₀cβ)

e dove le p_x ecc., sono i soliti operatori differenziali. Si dimostra, mediante le relazioni di anticommutazione, che vale la solita relazione energia-impulso (E/c)² = p² + (mc)². L'equazione si può generalizzare facilmente al caso di elettroni su cui agisce un campo elettromagnetico esterno. L'equazione tiene conto dello spin dell'elettrone e del momento magnetico intrinseco a esso associato, per il quale essa dà nel modo più naturale il rapporto giromagnetico corretto. Si può poi riprendere lo studio dell'atomo di idrogeno e si ritrovano così, in forma più esatta, gli effetti di struttura fine, dovuti alla variabilità della massa e all'interazione spin-orbita; anche il cosiddetto fattore di Thomas vien fuori nel modo più naturale. Non possiamo qui soffermarci sulle numerosissime applicazioni dell'equazione di Dirac nella teoria della diffusione degli elettroni, dei raggi gamma, ecc., o dell'urto radiativo (formule relativistiche di Mott, di Klein-Nishijina, di Møller, di Bhabha, di Bethe-Heitler, ecc.).

c) Problemi della meccanica quantistica relativistica.

La descrizione corretta delle interazioni relativistiche fra particelle presenta problemi di un ordine di grandezza superiore rispetto a quelli così elegantemente risolti dall'equazione di Dirac. Le funzioni d'onda di Schrödinger per n corpi sono state estese con qualche successo ai problemi relativistici. In realtà non esiste un vero problema degli n-corpi relativistico, in quanto i processi di creazione e di distruzione di particelle intervengono in modo essenziale. Una descrizione completa delle interazioni relativistiche oggi sembra possibile solo in base alla teoria quantistica dei campi (v. particelle elementari: Campi e particelle), teoria in cui i campi d'onda riappaiono non come ampiezze di probabilità, ma nel loro ruolo classico di grandezze fisiche (con certe limitazioni), ossia, nella teoria quantizzata, come operatori dipendenti da x, y, z, t. L'ultimo ventennio ha visto un pullulare di indirizzi, che si attengono sostanzialmente a quest'idea ('assiomatica dei campi') o se ne allontanano ('teoria pura della matrice S', che riduce tutto a fenomeni d'urto o quasi), talvolta anche in modo radicale.

Il progresso della teoria dei campi fu a lungo ostacolato dalle cosiddette ‛divergenze': il calcolo di qualsiasi processo porta a un risultato non finito, qualora si spinga l'approssimazione oltre un certo limite. Poi venne scoperta la ‛rinormalizzazione', un modo elegante di aggirare la difficoltà, che ha aperto la via a straordinari progressi nell'elettrodinamica quantistica. Si sono così potuti calcolare vari effetti, specialmente nel campo della spettroscopia, con precisione quasi incredibile. Per quel che riguarda le interazioni forti (nella fisica nucleare o delle particelle elementari) la rinormalizzazione rimane un'idea interessante, che è servita a chiarire alcune questioni, ma che non viene mai portata sino in fondo ‛per difficoltà tecniche'. In ultima analisi, sembra impossibile che la difficoltà delle divergenze non si possa superare in modo più radicale. Forse la compatibilità formale tra la teoria della relatività e la teoria dei quanti è soltanto un'illusione che nasconde più profonde sorprese. È difficile dire fino a che punto e in quale direzione sia necessario modificare le basi stesse della teoria oggi esistente. La meccanica quantistica, con la sua straordinaria messe di risultati, rimarrà in ogni caso un passo avanti definitivo, nello stesso senso in cui lo sono state la dinamica e l'elettrodinamica classiche.

Bibliografia.

Bargmann, V., On unitary ray representations of continuous groups, in ‟Annals of mathematics", 1954, LIX, pp. 1-46.

Bell, J. S., On the Einstein Rosen Podolsky paradox, in ‟Physics", 1964, I, pp. 195-200.

Bohr, N., On the constitution of atoms and molecules, in ‟Philosophical magazine", 1913, XXVI, pp. 1-25, 476-502, 857-875.

Condon, E. U., Shortley, G. H., The theory of atomic spectra, Cambridge 1935.

Dirac, P. A. M., The principles of quantum mechanics, Oxford 1930.

Estermann, I., Stern, O., Beugung von Molekularstrahlen, in ‟Zeitschrift für Physik", 1930, LXI, pp. 95-125.

Feynman, R. P., Hibbs, A. R., Quantum mechanics and path integrals, New York 1965.

Frisch, R., Experimenteller Nachweis des Einsteinschen Strahlungsrückstosses, in ‟Zeitschrift für Physik", 1933, LXXXIV, pp. 42-48.

Klein, M., Paul Ehrenfest, Amsterdam 1970.

Kramers, H. A., Die Grundlagen der Quantentheorie, Leipzig 1939.

Mott, N. F., Elements of wave mechanics, Cambridge 1962.

Pauli, W., Die allgemeinen Prinzipien der Wellenmechanik, Berlin 1933, 1958².

Persico, E., Fondamenti della meccanica atomica, Bologna 1939.

Waerden, B. L. van der, Die Grappentheoretische Methode in der Quantenmechanik, Berlin 1931.

Waerden, B.L. van der, Sources of quantum mechanics, Amsterdam 1967.

Wigner, E. P., On unitary representations of the inhomogeneus Lorentz group, in ‟Annals of mathematics", 1939, XL, pp. 149-204.

Wigner, E. P., Group theory and its application to the quantum theory of atomic spectra, New York 1959.

Wigner, E. P., On hidden variables and quantum mechanical probabilities, in ‟American journal of physics", 1970, XXXVIII, pp. 1005-1009.

Elettrodinamica quantistica

SOMMARIO: I. Introduzione. □ 2. Principi generali dell'elettrodinamica quantistica: a) significato fisico dell'equazione di commutazione; b) livelli energetici del campo libero; c) seconda quantizzazione. □ 3. Applicazioni fisiche e metodi matematici: a) matrice S e regole at Feynman; b) funzioni di Green e proprietà del vuoto. □ 4. La rinormalizzazione: confronto con l'esperienza e significato fisico dei risultati. □ Bibliografia.

1. Introduzione.

L'elettrodinamica quantistica risulta dall'applicazione dei principî della meccanica quantistica al campo elettromagnetico; essa permette di sviluppare una dinamica relativistica degli elettroni logicamente coerente. Anche nel caso dei muoni (o mesoni μ) valgono sostanzialmente gli stessi principî e le stesse formule, salvo beninteso le differenze dovute alla diversa massa delle particelle. L'estensione della teoria ad altre particelle, per esempio ai protoni, presenta invece seri problemi, dovuti alle cosiddette interazioni forti (v. particelle elementari).

La necessità di una teoria relativistica in questo settore della fisica non è soltanto una questione di principio. Si sa infatti, sin dal 1916, anno di pubblicazione di un celebre lavoro di Sommerfeld, che la struttura fine delle righe spettrali, come del resto quella dei raggi X caratteristici di un elemento, dipende da effetti relativistici. Una teoria relativistica è poi ovviamente indispensabile per interpretare i fenomeni d'urto che riguardano particelle dotate di velocità v assai vicina a quella della luce (raggi cosmici, fisica delle alte energie). Negli atomi leggeri le velocità degli elettroni sono dell'ordine di e²/ℏ e il rapporto v/c è quindi dell'ordine della ‛costante di struttura fine' α = 1/137; gli effetti relativistici, che sono proporzionali a (v/c)², sono pertanto assai piccoli, ma ciononostante interessantissimi per la regolarità e la ricchezza delle strutture che ne risultano (v. atomo). Sono effetti relativistici la variabilità della massa con la velocità, l'interazione spin-orbita e le deviazioni dalla legge di Coulomb dell'interazione tra due elettroni in moto, deviazioni che derivano sia dal fatto che un elettrone in moto produce un campo magnetico, sia dal ritardo dell'interazione, dovuto alla velocità finita, uguale a c, di propagazione delle interazioni elettromagnetiche.

Sebbene non siano mancati tentativi in altre direzioni, è chiaro che la strada maestra da seguire è l'introduzione del campo elettromagnetico maxwelliano come parte integrale del sistema dinamico. Ciò significa naturalmente che, se si vuole andare al di là della teoria classica di Maxwell-Lorentz, bisogna ‛quantizzare' non solo il moto degli elettroni ma anche il campo (v. cap. 2), considerando le equazioni di Maxwell come equazioni del moto nel senso di Heisenberg, equazioni cioè nelle quali le sei componenti del campo (E, H) e le quattro componenti della quadricorrente non sono più funzioni numeriche del punto x e del tempo t, ma sono funzioni i cui valori sono matrici, o, se si vuole, operatori lineari in uno spazio vettoriale (di Hilbert) a infinite dimensioni. Poiché inoltre il sistema possiede in tal caso, anche nel senso classico, un numero infinito di gradi di libertà, lo schema quantistico che ne risulta è, pur prescindendo dalle difficoltà (divergenze) di cui parleremo, enormemente più complicato dell'ordinaria meccanica quantistica. Ne consegue che una determinazione esatta dei livelli energetici e delle corrispondenti autofunzioni, nel senso di Schrödinger, del sistema totale, oppure una determinazione esatta degli operatori di campo come funzioni del tempo, nel senso di Heisenberg, è fuori d'ogni possibilità, salvo nel caso banale, come vedremo, del ‛campo libero'. Se, ciononostante, si posseggono per vari problemi soluzioni utili (confrontabili coi dati sperimentali) e in certi casi di straordinaria precisione, ciò è dovuto in modo essenziale all'impiego del metodo delle perturbazioni, mediante il quale, partendo dal caso del campo libero come approssimazione d'ordine zero, si sviluppano le grandezze desiderate (le ampiezze di transizione, per esempio) in serie di potenze della carica e dell'elettrone, che compare come costante di proporzionalità nei termini di accoppiamento tra campo elettromagnetico ed elettroni. Lo sviluppo si rivela in ultima analisi come uno sviluppo rispetto alla già citata costante α, la cui piccolezza è poi la ragione ultima della rapida convergenza che il metodo ha in pratica (sulla convergenza in senso stretto si sa poco o nulla; esiste solo un'opinione abbastanza diffusa che si tratti solo di serie asintotiche).

Il metodo delle perturbazioni da solo ha però una portata assai limitata; nelle approssimazioni superiori è impossibile applicarlo a causa delle ‛divergenze' (v. capp. 3 e 4). Il ricorso sistematico, a partire dal 1947, al concetto di ‛rinormalizzazione' ha permesso di aggirare la difficoltà, allargando enormemente il campo di applicazione dell'elettrodinamica quantistica e consentendo di raggiungere quella precisione dei risultati a cui si è accennato. Lo sviluppo storico della teoria viene così a dividersi in due periodi ben distinti.

Nel primo periodo le divergenze vengono considerate come un ostacolo che può venir superato solo grazie a una revisione radicale dello schema teorico a livello delle distanze molto piccole o (cosa equivalente, secondo il principio di complementarità) a quello delle transizioni con scambi molto grandi della quantità di moto e dell'energia; non si ha quindi una grande fiducia nel significato fondamentale dello schema e si arriva talvolta perfino a dubitare dell'esistenza di quei fenomeni, come le ‛fluttuazioni del campo' nel vuoto o la ‛polarizzazione del vuoto' (v. cap. 3, È b), che lo schema prevede chiaramente in modo qualitativo, ma che non può calcolare a causa delle divergenze. Quanto alle applicazioni, ci si limita naturalmente a calcolare tutto quello che ha un valore finito, il che significa invariabilmente che si arresta la serie perturbativa per il processo in questione al primo termine significativo all'‛ordine più basso'; questo ordine dipende dal processo studiato. (Nella notazione dei grafici lineari di Feynman, di cui diremo più avanti, ciò significa limitarsi a grafici semplicemente connessi - i cosiddetti trees di Cayley - ossia i grafici non contenenti alcun circuito chiuso; di qui l'espressione tree approximation. A ogni circuito chiuso corrisponde un'integrazione nello spazio dei momenti). Anche se il metodo in questione non consente una precisione grandissima, alcuni dei risultati ottenuti sono tuttavia assai importanti (v. tab. I).

Nel 1947 Lamb e Retherford annunciarono di aver osservato, con la tecnica delle microonde, uno spostamento del livello 2²S_1/2 dell'atomo di idrogeno rispetto al livello 2²P_1/2; i due livelli, secondo la consueta trattazione del problema mediante l'equazione di Dirac, sarebbero dovuti coincidere (v. fig. 1).

Questa scoperta e la scoperta quasi contemporanea dell'anomalia del momento magnetico dell'elettrone (P. Kusch e H. Foley) segnano l'inizio del secondo periodo dell'elettrodinamica quantistica. Come oggi possiamo dire con sicurezza, si tratta in entrambi i casi di una ‛correzione radiativa', cioè di uno di quegli effetti dell'interazione tra elettroni e radiazione che compaiono solo agli ‛ordini superiori'. La constatazione della reale esistenza di effetti siffatti, e la possibilità di misurarli con insperata precisione, rinnovarono naturalmente l'interesse per una teoria che ne aveva, se non altro, previsto qualitativamente l'esistenza e in un certo senso anche l'ordine di grandezza. Si scoprì così, con una certa sorpresa, che il problema delle divergenze nascondeva concetti fisici più profondi di quanto si supponesse. L'eliminazione sistematica delle divergenze avviene mediante la rinormalizzazione della carica (Dirac, 1934) e della massa (Kramers, 1937) secondo diverse proposte, non del tutto nuove, avanzate da vari autori. Alcuni dei risultati più importanti così ottenuti sono riassunti nella tab. II.

2. Principi generali dell'elettrodinamica quantistica.

Volendo impostare la teoria generale su concetti già in parte acquisiti, si presentano due possibilità ‛a prima vista assai diverse. Si potrebbe assumere come concetto elementare di partenza il fotone, particella di massa nulla, la cui equazione di Schrödinger deve possedere, per ogni dato valore del momento k, due soluzioni indipendenti, corrispondenti a due stati di polarizzazione diversi; oppure - come già si è detto - si può partire dall'idea di campo elettromagnetico, considerato come sistema dinamico accoppiato agli elettroni.

Nel primo caso, ignorando dapprima gli elettroni, si potrà costruire uno schema analogo a quello di Schrödinger per il problema degli n corpi: non solo gli stati di un fotone, ma anche quelli di un sistema di due o più fotoni sono allora descritti da opportune funzioni d'onda, che, nel caso di n fotoni, dovranno dipendere dagli z punti x₁, x₂..., x_n (oppure, passando allo spazio dei momenti, dai corrispondenti n vettori d'onda k₁, k₂, ..., k_n) e inoltre dagli n indici di polarizzazione degli n fotoni. Queste funzioni dovranno inoltre essere ‛simmetriche' rispetto allo scambio delle variabili relative a due qualsiasi fotoni; questa restrizione dà infatti il corretto conteggio dei livelli di un sistema di n fotoni, corrispondente alla legge di Planck (statistica di Bose-Einstein; v. quanti, teoria dei: Meccanica quantistica). In questo schema, se vi sono elettroni, bisognerà far dipendere la funzione d'onda anche dalle variabili che descrivono gli elettroni; l'interazione tra elettroni e fotoni viene allora descritta da termini che accoppiano la funzione d'onda di n fotoni con quelle relative a n ± 1 fotoni. Questi termini di accoppiamento generano le transizioni, reali o virtuali, in cui un fotone viene creato e assorbito.

Partendo invece dal campo elettromagnetico inteso, come nella teoria classica, quale sistema dinamico a infiniti gradi di libertà, bisognerà quantizzare questo sistema nel senso già indicato nell'introduzione.

Il metodo preferito da Fermi, nelle sue note lezioni, per porre in evidenza l'analogia del campo elettromagnetico con un ordinario sistema dinamico si basa sull'osservazione ben nota che il campo racchiuso entro una cavità vuota a pareti riflettenti si può considerare come una sovrapposizione di infiniti campi parziali, distinti da un indice s = 1, 2, ..., ognuno dei quali compie oscillazioni sinusoidali con una sua frequenza caratteristica ν_s Questo comportamento è del tutto simile a quello di un sistema dinamico che compie piccole oscillazioni intorno a una posizione di equilibrio.

Ognuno dei campi parziali, considerato da solo, corrisponde a un'onda elettromagnetica stazionaria, che ha una sua caratteristica distribuzione nello spazio. Così, per esempio, il potenziale vettore A (x, t), da cui si deduce di solito il campo magnetico H = rot A, si può esprimere a un dato istante mediante una serie in cui, nel caso generale, vanno incluse sia onde trasversali (div a = 0) sia onde longitudinali (rot a 0):

in questa serie i termini corrispondenti a s = 1, 2,... sono appunto i campi parziali; le funzioni caratteristiche a_s si ottengono risolvendo un problema di autovalori legato alla forma e alle dimensioni della cavità, problema del resto ben noto in radiotecnica (microonde, ecc.). I coefficienti q₁, q₂, ..., q_s, ... dello sviluppo si possono considerare come coordinate lagrangiane generali del sistema o, se si vuole, come le coordinate di altrettanti oscillatori, che nel loro insieme costituiscono il campo elettromagnetico. Le ‛equazioni del moto' di questi oscillatori, in forma sia lagrangiana sia hamiltoniana, altro non sono che le equazioni di Maxwell in veste diversa.

Le oscillazioni dei campi parziali non saranno più indipendenti le une dalle altre (né strettamente sinusoidali) se entro la cavità vi sono elettroni, o altre particelle cariche, le quali generano le densità di carica e di corrente che compaiono come termini non omogenei a secondo membro delle equazioni di Maxwell:

In questa situazione la presenza delle cariche e i loro movimenti modificano il campo, mentre questo a sua volta agisce sul moto delle cariche; indirettamente, ne risulta un accoppiamento tra i vari oscillatori del campo.

Nella forma hamiltoniana delle equazioni del moto compaiono, accanto alle q₁, q₂, ..., le variabili coniugate p₁, p₂, ..., le quali sono del resto uguali, a parte il segno, ai coefficienti dello sviluppo, analogo alla (1), del campo elettrico E a un dato istante:

La quantizzazione di questo schema avviene ora, secondo un'idea già analizzata da Born, Heisenberg e Jordan, e poi molto più ampiamente da Dirac (1927), Heisenberg e Pauli (1929) e Fermi (1929), estendendo alle variabili q_s, p_s (s = 1, 2, ...) le regole di commutazione già ammesse per gli ordinari sistemi dinamici a n gradi di libertà, in particolare, per una q_s e il corrispondente momento p_s la regola:

[q_s, p_s] = q_sp_s − p_sq_s = i ℏ, (4)

mentre, invece, q_s e p_s (con s ≠ r), due diverse q o due diverse p commutano una coll'altra. Beninteso, ciò implica che i valori delle q e delle p a un dato istante non siano ordinari numeri reali ma elementi di un'algebra non commutativa, più precisamente matrici o anche operatori lineari in uno spazio hilbertiano.

a) Significato fisico dell'equazione di commutazione.

Conclusioni analoghe a quelle testé illustrate valgono ovviamente, grazie alle relazioni (1) e (3), per le componenti E_i(x) e H_k(x′) (i, k = 1, 2, 3) del campo elettrico e magnetico in due qualsiasi punti dello spazio. In realtà il valore di un campo in un punto esattamente definito è un'astrazione, cui converrà sostituire, seguendo Bohr e Rosenfeld, un valore medio Ä o Èk′ su una regione finita τ o τ′ dello spazio-tempo. Se le regioni τ e τ′ sono ‛causalmente indipendenti', se cioè un segnale non può propagarsi da un punto di τ a uno di τ′ o viceversa con velocità non maggiore di c, allora si trova che Ä_i e Èk′ commutano tra loro e quindi, secondo i principi generali, sono grandezze misurabili indipendentemente. Nel caso opposto, supponiamo addirittura che le due medie siano fatte sulla stessa regione r di dimensioni lineari R; si trovano allora relazioni di complementarità tra componenti mutuamente ortogonali dei campi E e H del tipo seguente:

in cui ΔE_x e ΔH_y rappresentano l'indeterminazione, secondo Heisenberg, nella misura delle suddette componenti. L'indeterminazione è dunque tanto più grande, quanto più piccola è la regione τ.

b) Livelli energetici del campo libero.

Una volta quantizzato il sistema, quali sono i suoi livelli energetici nell'approssimazione del campo libero, ossia in assenza di cariche? Lo stato di energia minima, per il sistema complessivo, è evidentemente quello che si ottiene supponendo che ogni oscillatore si trovi nel suo stato fondamentale. Misuriamo sempre l'energia totale del sistema a partire da questo stato (lo stato ‛vuoto'). L'energia d'eccitazione totale del sistema si ottiene sommando le energie di eccitazione parziale E_s dei singoli oscillatori; queste sono a loro volta multipli interi dei rispettivi quanti d'oscillazione ε_s = hν_s. Il sistema complessivo possiede quindi livelli energetici caratterizzati da infiniti numeri quantici n₁, n₂, ..., n_s, ... secondo la formula:

somma in cui però solo un numero finito di interi n₅ potrà essere diverso da zero, essendo la E finita.

Si riconosce ora facilmente che questo risultato, ottenuto col metodo della quantizzazione del campo, è identico a quello che si avrebbe con il primo metodo, per un numero n di fotoni uguale alla somma finita Σ_nn_s. Si trova infatti che il classico problema di autovalori delle onde stazionarie è in sostanza il problema di autovalori di Schrbdinger per il singolo fotone racchiuso nella cavità e le a_s (x) sono le corrispondenti autofunzioni. Il linguaggio è diverso, ma il risultato è lo stesso: nel secondo metodo le ε_s sono, per s = 1, 2, ..., i livelli energetici del singolo fotone, le n_s sono non numeri quantici, ma ‛numeri di occupazione' e così via.

c) Seconda quantizzazione.

La completa equivalenza dei due metodi illustrati nel paragrafo precedente sussiste anche nel caso del campo interagente con gli elettroni (Dirac, 1927). La prova, invero assai meno ovvia, estende l'equivalenza dal caso dei fotoni a quello di un sistema di particelle identiche, purché valga la statistica di Bose-Einstein. Le particelle possono per esempio essere di massa non nulla e interagire l'una con l'altra mediante un potenziale qualsiasi. Nel caso non relativistico si parte allora dalla ψ(x, t) di Schrödinger considerandone la parte reale e immaginaria come due campi nel senso classico, ossia come grandezze fisiche, e in seguito quantizzando il sistema di questi due campi in modo analogo a quanto si è fatto per il campo di Maxwell.

Questo metodo, detto di ‛seconda quantizzazione', può anche venire applicato, mutatis mutandis, alla ψ di Dirac per l'elettrone, o, più generalmente, al caso di sistemi di particelle identiche, che obbediscono al principio di esclusione e quindi alla statistica di Fermi. Ciò che va cambiato, a questo scopo, è la forma delle relazioni (4) che diventano (Jordan e Wigner) ‛relazioni di anticommutazione', strettamente connesse con le algebre inventate, per tutt'altro scopo, da Clifford nel secolo scorso. Lo schema che ne risulta è allora, nel caso più semplice, il seguente.

Siamo in presenza di due campi d'onda di natura diversa (il cosiddetto ‛sistema dei due campi' a cui ci riferiremo in seguito), in interazione l'uno con l'altro: il campo elettromagnetico (E, H) e il campo di Dirac dotato di quattro componenti ψ_ρ(ρ = 1, 2, 3, 4). Ognuno di questi campi possiede non solo proprietà ondulatorie, ma anche - una volta quantizzato - proprietà corpuscolari; i ‛quanti' del campo ψ sono naturalmente gli elettroni. Dirac stesso riconobbe inoltre, con audace intuizione, che il campo ψ descrive allo stesso tempo anche particelle di carica elettrica opposta o ‛antielettroni'; se si esamina l'espressione di Dirac per la corrente associata al campo ψ, si vede che oltre alle consuete transizioni in cui l'emissione, o l'assorbimento, di un fotone è accompagnata da un salto quantico di un elettrone da uno stato di movimento a un altro, la teoria prevede necessariamente anche transizioni in cui un elettrone viene creato o distrutto insieme a un antielettrone. La legge di conservazione della carica elettrica sarà ugualmente rispettata se la somma algebrica delle cariche della coppia è esattamente nulla. Inoltre, sebbene ciò non appaia chiaramente nella presentazione originale delle idee di Dirac, si può mostrare che la teoria possiede una profonda simmetria rispetto alle due particelle, dimodoché, in particolare, esse debbono avere esattamente la stessa massa (H. Weyl). Ciò che sembrava a prima vista una difficoltà, non essendo nota una particella con le proprietà dell'antielettrone, divenne un trionfo della teoria, allorché K. Anderson scoprì il positone, il quale possiede non solo la carica e la massa volute, ma anche esattamente tutte le proprietà richieste dalla teoria di Dirac (v., per es., gli effetti 2 e 6 della tab. I).

Notiamo ancora che lo schema illustrato possiede le necessarie proprietà formali di invarianza relativistica, esaminate esaurientemente da vari autori (Heisenberg e Pauli, nel 1929, e, più recentemente, Tomonaga, Schwinger e altri). Esso è invariante anche rispetto alle trasformazioni dei potenziali (Eichinvarianz di Weyl, o gauge invariance degli autori anglosassoni), già note dalla teoria classica, e possiede inoltre, come si è detto, una simmetria rispetto alla carica delle particelle, detta ‛coniugazione di carica', che è una completa novità. Il concetto di antiparticella, confermato dalla scoperta del positone, e più tardi da quella dell'antiprotone, dell'antineutrone, ecc. è un importante contributo dell'elettrodinamica quantistica alla fenomenologia delle particelle elementari.

3. Applicazioni fisiche e metodi matematici.

L'esame delle applicazioni dello schema ora descritto a problemi concreti non si può facilmente separare da quello dei metodi impiegati. La teoria delle perturbazioni, ossia lo sviluppo in serie di potenze della costante e di accoppiamento, può assumere forme assai diverse, a seconda delle grandezze in esame. Nella meccanica non relativistica il concetto di ‛vettore di stato' o funzione d'onda ha una posizione centrale; si hanno pertanto due note forme di sviluppo: della funzione d'onda di uno stato non stazionario, supposto dato lo stato iniziale (teoria delle perturbazioni di Dirac), oppure delle funzioni d'onda degli stati stazionari, ossia delle autofunzioni dell'operatore energia e dei corrispondenti autovalori (teoria delle perturbazioni di Schrödinger). Nella teoria relativistica ci si è allontanati sempre di più da questi schemi; converrà però ricordarne qui un classico esempio, per quegli aspetti qualitativi che sopravvivono a tutti i cambiamenti della tecnica.

Nella teoria (di Wigner-Weisskopf) dell'allargamento delle righe spettrali, dovuto all'interazione tra l'atomo e la radiazione, il calcolo, secondo gli schemi suaccennati, indica che, oltre a un allargamento, si ha anche uno spostamento radiativo dei livelli (che sarà poi l'effetto osservato molto più tardi da Lamb) e quindi delle righe spettrali. Lo spostamento si presenta come un effetto del secondo ordine in e (ossia proporzionale alla costante α) dovuto a transizioni virtuali in cui viene emesso e successivamente riassorbito un fotone. Se si considera che l'elemento di matrice per l'emissione o l'assorbimento di un fotone contiene un fattore v/c e che in un atomo idrogenoide di carica nucleare Ze questo fattore è ≃ Zα si può concludere che l'effetto dev'essere dell'ordine di grandezza α(Zα)² rispetto all'energia di legame. In realtà questa valutazione è illusoria, perché l'espressione da calcolarsi contiene un'integrazione sullo spazio dei momenti (del fotone virtuale) che diverge al limite superiore; si può ovviamente ottenere un risultato finito mediante un ‛taglio' alle alte energie, ma la teoria non offre alcuna giustificazione per questo taglio, né un'idea sufficientemente esatta della sua posizione, da cui il risultato ovviamente dipende.

Un rimedio assai più soddisfacente ci è offerto dalla cosiddetta ‛rinormalizzazione' (v. cap. 4; v. anche particelle elementari: Campi e particelle), ma anche usando questo procedimento è assai facile arrivare a risultati ambigui. Questo pericolo può essere evitato, se ci si lascia guidare dal principio secondo cui le proprietà di invarianza della teoria (in particolare l'invarianza relativistica) devono venir salvaguardate a ogni passo. Ciò non è possibile nell'ambito del formalismo tradizionale ed è questa una delle principali ragioni per l'adozione di nuovi metodi.

a) Matrice S e regole di Feynman.

La matrice S e le funzioni di Green in senso lato sono fra i principali strumenti formali di cui si serve la teoria delle perturbazioni. La matrice S, o matrice d'urto, riunisce in un solo schema le ampiezze di probabilità di tutti i possibili fenomeni d'urto in cui intervengono come particelle ‛incidenti' (stato iniziale) o ‛uscenti' (stato finale) fotoni, elettroni e positoni. Nell'ambito dell'elettrodinamica quantistica pura è anche possibile far intervenire nell'urto un protone o altro nucleo atomico, se si è disposti a schematizzarne l'effetto considerando il nucleo come la sorgente di un campo elettrostatico esterno. Possiamo pensare che lo stato iniziale sia specificato assegnando la quantità di moto e lo stato di polarizzazione (ossia una componente dello spin) di ogni particella, e lo stato finale in modo analogo. L'insieme dei dati che caratterizzano uno stato si può indicare con una sola lettera, come a, b, ecc.; si può allora designare con il simbolo S_ab l'ampiezza di probabilità per la transizione dallo stato iniziale b allo stato finale a. La matrice S non è altro che l'insieme di questi simboli disposti come gli elementi di una matrice (Sab). Si dimostra che l'operatore rappresentato da questa matrice è unitario e relativisticamente invariante. La prima di queste proprietà corrisponde alla proposizione, intuitivamente ovvia, che la somma delle probabilità di tutti i possibili stati finali deve essere uguale a uno, qualunque sia lo stato iniziale (che può anche essere una combinazione lineare di diversi stati b); la seconda corrisponde al fatto ugualmente intuitivo che la relazione tra stato finale e stato iniziale è indipendente dal sistema di riferimento.

Una delle forme invarianti della teoria delle perturbazioni, dovuta a Dyson, consiste nello sviluppare in serie di potenze di e l'operatore S; il termine d'ordine zero è l'unità (il che significa che senza interazione non vi sono urti: lo stato iniziale è uguale a quello finale). Si ha cioè:

S = 1 + eS₁ + e²S₂ +... (6)

Si mostra inoltre che, in assenza di un campo esterno, è S₁ = 0, cioè tutti i processi cominciano almeno al second'ordine (effetto Compton, ecc.; v. tab. I). Il risultato più importante di questo metodo è una deduzione particolarmente semplice delle ‛regole di Feynman', di cui si dirà più avanti.

Per la sua stessa natura, il formalismo della matrice S si presta particolarmente bene allo studio degli urti tra particelle libere, meno bene a quello degli stati legati, come, per esempio, gli stati dell'atomo di idrogeno. Per questa e altre ragioni, sono stati sviluppati formalismi più generali; esamineremo in particolare quelli che si fondano sulle ‛funzioni di Green' di due o più argomenti. Queste sono funzioni G(x, y), G(x, y, z), ..., dove x, y, z, ... sono punti arbitrari dello spazio-tempo. Tra l'altro, le funzioni G(x, y) di due argomenti, dette anche ‛propagatori di Feynman', sono necessarie per formulare in modo generale le regole di Feynman per il calcolo dei terminiS₁, S₂,... della matrice S.

Possiamo però sin d'ora illustrare queste regole in due casi particolari mediante una considerazione molto semplice, dovuta anch'essa a Feynman. Consideriamo la descrizione, secondo la teoria convenzionale delle perturbazioni, di due tipici processi: l'urto elastico tra due elettroni e l'effetto Compton.

Le ‛regole' si formulano mediante l'uso dei ‛grafici' o diagrammi lineari, introdotti anch'essi soprattutto da Feynman (per una descrizione generale di questi grafici v. particelle elementari). Nella fig. 2, A e B, rappresentiamo graficamente due diverse successioni nel tempo di processi virtuali, che possono dare luogo all'urto elastico tra due elettroni. Nella fig. 2A, cominciando dal basso, vediamo due linee che rappresentano i due elettroni prima dell'urto. All'istante t₁ avviene una transizione virtuale in cui l'elettrone di sinistra emette un fotone (rappresentato dalla linea ondulata); il cambiamento del momento dell'elettrone, richiesto dalle leggi di conservazione, è rappresentato qualitativamente dal cambiamento di direzione della linea che rappresenta l'elettrone. All'istante successivo, t₂, avviene una nuova transizione in cui il fotone scompare, mentre l'elettrone di destra a sua volta subisce un cambiamento del momento. Le due linee in alto corrispondono allo stato dopo l'urto. La fig. 2B descrive ovviamente una sequenza molto simile, in cui l'elettrone di sinistra (o, più chiaramente, l'elettrone che ha inizialmente il momento p₁) assorbe, invece di emettere, il fotone virtuale; i due elettroni, insomma, si scambiano le parti, ma i loro momenti iniziali e finali restano gli stessi come nel primo caso.

Vediamo ora cosa avviene quando, calcolando secondo la teoria già nota delle perturbazioni, si sommano i contributi dei due diagrammi. Secondo le leggi di conservazione, il momento q = p₁ − p1′ (=p₂′ − p₂) ‛trasmesso' nell'urto dal primo al secondo elettrone è, nella fig. 2A, uguale al momento del fotone virtuale e, nella fig. 2B, uguale allo stesso cambiato di segno. In entrambi i casi l'energia del fotone, calcolata in base al suo momento, è uguale a c ∣q∣, o più semplicemente ∣q∣, usando unità relativistiche (in cui è c = 1).

In questo calcolo vecchio stile, nello stato intermedio tra le due transizioni virtuali non si ha conservazione dell'energia; la differenza tra l'energia dello stato intermedio (ossia nel caso A : E₁¹ + E₂ + ∣q∣) e quella dello stato iniziale E₁ + E₂ compare a denominatore nell'ampiezza di probabilità corrispondente. Ai due diagrammi A e B corrispondono due denominatori diversi; a parte questo, l'ampiezza contiene altri fattori, che sono esattamente gli stessi per i due diagrammi e rappresentano gli elementi di matrice per l'emissione o l'assorbimento del fotone e la loro dipendenza dallo spin iniziale e finale dei due elettroni. In particolare, i due elementi di matrice presenti in entrambi i diagrammi contengono ognuno un fattore di proporzionalità (2 ∣q∣)^-1/2. Se ora usiamo l'energia ε = E₁ − E₁′ trasmessa dal primo al secondo elettrone (energia che per la legge di conservazione è anche uguale a E₂¹ − E₂) per esprimere i due denominatori summenzionati, vediamo che la somma dei contributi di entrambi i diagrammi contiene termini che si semplificano come segue:

A questo risultato le ‛regole di Feynman' arrivano direttamente, considerando in primo luogo A e B come un unico diagramma (ignorando cioè la scala dei tempi e tenendo conto solo della struttura ‛topologica' dei diagrammi) e assegnando poi alle varie parti del diagramma (linee incidenti e uscenti, vertici e linea interna che congiunge i due vertici) determinati valori, come quelli forniti, per esempio, dalla (7).

È questo un aspetto dei diagrammi su cui non si insiste mai abbastanza: al fisico sperimentale e, in genere, al non iniziato essi appaiono sovente come ‛fumetti' atti a suggerire un'interpretazione intuitiva del contenuto fisico della teoria; in realtà si tratta piuttosto di ideogrammi contenenti precise istruzioni per il calcolo di certe quantità.

Tornando alla (7), si noti in particolare che il denominatore della formula finale altro non è che il quadrato (nel senso di Minkowski) del quadrivettore momento trasmesso dal fotone virtuale. In una discussione più approfondita, l'espressione si presenta come la trasformata di Fourier del propagatore per il campo maxwelliano.

Esaminiamo analogamente due diagrammi relativi all'effetto Compton (v. fig. 3, A e B), che, come nel caso precedente, sono topologicamente identici. (In entrambi i casi vi sono altri due diagrammi, che non prendiamo in considerazione e che differiscono da quelli qui riprodotti per una diversa assegnazione delle linee esterne). Nella fig. 3A l'elettrone incidente di momento p emette, nella prima transizione all'istante t₁, il fotone finale di momento k′, assumendo quindi un valore del momento pari a p − k′. Successivamente, il fotone iniziale, di momento k, viene assorbito dall'elettrone, che passa così allo stato finale, di momento p − k′ + k = p′. Nella fig. 3B il primo atto virtuale è l'assorbimento del fotone iniziale, con produzione immediata dell'elettrone finale, ma non è l'elettrone iniziale che compie la transizione; questa può descriversi invece come la creazione virtuale di un antielettrone, ossia di un positone, rappresentato, secondo il pittoresco linguaggio feynmaniano, dalla linea interna che ‟va indietro nel tempo". Nella transizione successiva, il positone virtuale si annichila insieme all'elettrone incidente, generando il fotone finale.

Lo stato intermedio in questi due diagrammi è assai diverso; nel caso illustrato in A nell'intervallo di tempo tra t₁ e t₂ sussistono contemporaneamente i due fotoni, iniziale e finale, più l'elettrone nello stato intermedio; nel caso illustrato in B, invece, al posto dei due fotoni si hanno contemporaneamente i due elettroni, iniziale e finale, e il positone virtuale. I soliti denominatori si deducono facilmente dai diagrammi, ma nell'esempio in questione sorgono ulteriori complicazioni (che non descriveremo) dovute alla struttura degli elementi di matrice. Ciononostante, anche in questo caso, sommando i due termini l'espressione si semplifica e a denominatore compare, come nella (7), il quadrato del quadrivettore momento trasmesso; vi sono tuttavia due differenze rispetto alla (7): dato che la linea intema è una linea ‛elettronica', invece che ‛fotonica', il denominatore ha la forma ∣q∣² − ε² − ε² + m², dove m è la massa di riposo dell'elettrone; inoltre a numeratore compaiono matrici relative allo spin. Sotto un altro punto di vista, le differenze ora rilevate sono quelle tra il propagatore per il campo ψ di Dirac e il propagatore per i fotoni incontrato prima.

Le regole di Feynman, su cui ritorneremo ancora (v. cap. 3, È b), ci insegnano che le semplificazioni incontrate negli esempi precedenti si estendono in modo del tutto inaspettato al caso più generale, in cui si possono avere successioni di transizioni virtuali di arbitraria complicazione, rappresentate naturalmente da grafici con un numero qualsiasi di vertici e di linee interne, mentre il numero delle linee esterne dipende naturalmente dal processo che si studia (numerosi esempi di grafici sono riportati nell'articolo particelle elementari e anche nel seguito di questo articolo). La contrazione delle formule dianzi riscontrata, quando diversi termini vengono riassunti in un singolo diagramma topologico, è tanto maggiore quanto più complicato è il diagramma. La semplificazione che ne risulta è in certi casi enorme; senza di essa, il calcolo degli ordini superiori, già pesante coi nuovi metodi, sarebbe del tutto impossibile.

b) Funzioni di Green e proprietà del vuoto.

Le funzioni di Green e concetti analoghi, usati da vari autori, servono per trattare, come si è accennato, aspetti della fisica dei campi che vanno al di là dello schema della matrice S. Si chiamano funzioni di Green anche le funzioni di due, tre, o più punti nello spazio dei momenti − G(p, q), G(p, q, r) ecc. - che si ottengono dalle G(x, y), ... mediante trasformazioni di Fourier multiple a quattro dimensioni (i momenti p, q, ecc. sono quadrimomenti). Gli elementi della matrice d'urto S si ottengono da queste funzioni mediante un particolare passaggio al limite.

La definizione delle funzioni di Green si basa sulle proprietà statistiche dello stato vuoto, di cui possiamo indicare il vettore rappresentativo col simbolo di Dirac ∣>; il vettore complesso coniugato viene allora indicato col simbolo 〈∣, dimodoché il valore probabile medio di una certa espressione,..., sarà dato dal prodotto scalare 〈∣ ... ∣>. Per esempio, il valore probabile medio nel vuoto del campo elettrico in un certo punto x dello spazio-tempo si indicherà con 〈∣E(x)∣>.

La funzione importante che ha lo stato vuoto nel formalismo della teoria dei campi ha ragioni molto semplici. Una è di natura formale: allo stesso modo come, nella teoria classica, una posizione di equilibrio serve come punto di partenza per lo studio delle piccole oscillazioni, così lo stato vuoto può servire da punto di partenza, formalmente, per lo studio degli stati contenenti una, due, tre, ... particelle. Questi stati possono cioè venir descritti come ‛eccitazioni' dello stato fondamentale, cioè come stati le cui autofunzioni si ottengono facilmente agendo con opportuni operatori su quella dello stato vuoto fondamentale. Specificamente, nel caso degli oscillatori armonici del campo elettromagnetico precedentemente descritti, l'‛operatore di creazione' per un quanto dell'oscillatore di indice s è della forma p_s + 2πiν_sq_s; si tratta in ultima analisi dell'operatore di campo A_μ(x), cui è stata applicata un'opportuna trasformazione di Fourier; in sostanza, dunque, gli stati di un fotone si ottengono mediante semplici operazioni lineari da una certa famiglia di stati della forma

∣ x, μ> = A_μ(x)∣>. (8)

Inoltre, ripetendo l'operazione, si ottengono gli stati contenenti due o più fotoni.

Storicamente, l'interesse per le proprietà fisiche dello stato vuoto deve la propria origine a due osservazioni. La prima riguarda l'esistenza di ‛fluttuazioni' del campo elettromagnetico, anche allo zero assoluto, ossia anche in assenza di radiazione (v.particelle elementari). Queste fluttuazioni esistono anche a prescindere dall'interazione fra i campi (ossia ponendo e = 0) e in questa approssimazione altro non sono che una manifestazione del fatto ben noto che un oscillatore armonico non può mai essere in uno stato di riposo assoluto. La seconda riguarda la reazione del vuoto a un campo esterno (generato per esempio dalla carica di un nucleo); il vuoto, infatti, definito come stato di minima energia non solo del campo elettromagnetico, ma anche del campo ψ di Dirac a esso accoppiato, reagisce a un campo elettrostatico esterno generando una distribuzione di cariche di polarizzazione, così detta per analogia col fenomeno della polarizzazione di un dielettrico. Più generalmente, se il campo esterno non è statico, ed è dunque descritto da un quadripotenziale A⁽e_μ⁾ (x), il vuoto reagisce generando una quadricorrente di polarizzazione. Ciò avviene grazie al meccanismo seguente: la quadricorrente osservata è il valore medio nel vuoto dell'operatore j^μ(x), che rappresenta la quadricorrente del campo elettrone-positone; le quattro componenti j^μ sono date da certe espressioni bilineari nel campo ψ e nel suo campo coniugato ψ. Ora queste espressioni bilineari hanno, come deve essere, valor medio nullo nel vuoto imperturbato, ma acquistano un valore diverso quando il campo di Dirac ψ e il suo coniugato ψ* vengono distorti dal campo esterno A^(e). Si genera così una quadricorrente di polarizzazione 〈∣ j^μ (x) ∣> che viene a sovrapporsi alla corrente classica esterna J^μ cui il campo A^(e) può venire attribuito. In prima approssimazione (se cioè il campo A^(e) non è troppo forte), si ha una relazione lineare tra corrente di polarizzazione e campo esterno, così come è lineare la relazione tra il campo e J^μ, pur essendo le due relazioni assai diverse. La relazione tra campo e corrente esterna (le equazioni di Maxwell) è una relazione differenziale locale, quella tra campo e corrente di polarizzazione,

〈∣ j^μ(x) ∣> = ∫ Π^μν (x − y)A⁽e_ν⁾(y) (dy), (9)

è una relazione integrale (non locale), il cui nucleo Π è il cosiddetto ‛tensore di polarizzazione' del vuoto. Ne segue che le distribuzioni spazio-temporali, o, nel caso statico, quelle spaziali, delle due quadricorrenti sono del tutto diverse. In particolare la carica di polarizzazione prodotta da una carica esterna puntiforme si estende su una regione le cui dimensioni sono dell'ordine della lunghezza d'onda Compton dell'elettrone ≃ 4 × 10^-11 cm). Il potenziale generato da questa distribuzione è d'altronde dell'ordine di α = 1/137 rispetto al potenziale esterno originario e dà luogo al ‛termine di Uehling' nell'effetto di Lamb e Retherford (v. tab. II). Tutti questi risultati si ottengono in forma finita solo dopo una rinormalizzazione della carica (v. cap. 4).

Da questo esempio si impara più in generale l'importanza della distinzione tra valori medi nel vuoto calcolati tenendo conto delle interazioni e, rispettivamente, ‛in approssimazione zero'. Questi ultimi si possono indicare col simbolo 〈 ... >₀. Tornando per esempio alle fluttuazioni del campo elettromagnetico, il metodo dei momenti ci insegna ad analizzarle calcolando i valori medi nel vuoto di prodotti di due, tre, o più componenti del campo, ma il risultato sarà diverso nelle due diverse approssimazioni di cui sopra. La differenza sta in questo: in primo luogo, lo stato vuoto, essendo descritto da un'autofunzione dell'operatore energia, sarà diverso a seconda che in questo operatore si includano i termini di interazione oppure no (in altre parole, la definizione, n₁ = n₂ = 0, del vuoto, usata nel cap. 2, È b, non è valida per i campi interagenti, in quanto n_s, con s = 1, 2, ..., non è un ‛buon numero quantico'); in secondo luogo, l'analisi delle fluttuazioni sarebbe incompleta se ci limitassimo a considerare prodotti di operatori di campo che si riferiscono a punti diversi nello spazio, ma allo stesso istante, ossia, per fare un esempio, prodotti come A(x)A(y), in cui i punti x e y dello spazio-tempo sono simultanei (x⁰ = y⁰). Supponiamo invece che sia x⁰ > y⁰; il valor medio del prodotto viene allora a dipendere dall'evoluzione degli operatori di campo nell'intervallo di tempo y⁰ 〈 t 〈 x⁰; questa evoluzione è determinata dalle equazioni del moto (nel senso di Heisenberg) che sono naturalmente diverse nelle due diverse approssimazioni dei campi liberi (e = 0) e dei campi interagenti. Resta inteso che nel calcolo dei valori medi 〈...>₀ si trascura l'interazione sia nelle equazioni del moto, sia nella definizione dello stato vuoto.

Siamo ora in grado di definire, nei casi più semplici, le funzioni di Green. Per il campo elettromagnetico si definisce una funzione di due punti, che è anche un tensore a due indici, D_μν(x, y), come segue. Se è x⁰ > y⁰, si pone:

D_μν(x, y) = 〈∣ A_μ(x) A_ν(y) ∣>. (10)

Se, invece, è x⁰ 〈 y⁰, si calcola il valor medio dopo aver invertito l'ordine dei fattori; in altre parole il campo relativo all'istante anteriore viene sempre scritto a destra (regola dell'ordine cronologico' dei fattori, che si estende al prodotto di n fattori). La funzione di Green così definita possiede la simmetria: D_μν(x, y) = D_νμ(y, x). Per il campo elettrone-positone si definisce analogamente una funzione di Green, G_ρσ (x, y), come il valor medio nel vuoto di una certa forma cronologicamente ordinata, bilineare nel campo ψ e nel suo coniugato (ρ e σ sono indici di Dirac spinoriali).

Un'interpretazione di queste definizioni, che ha il solo scopo di aiutare l'intuizione, si basa sull'osservazione che l'espressione a secondo membro della (10), per esempio, è anche il prodotto scalare dei due stati ∣x, μ> e ∣y, ν>, secondo la definizione (8). L'interpretazione probabilistica del prodotto scalare di due vettori di stato (v. quanti, teoria dei: Meccanica quantistica, eq. 37) ci porta a considerare la (10) come un' ampiezza di probabilità per un esperimento ideale di propagazione di un fotone, dal punto y al punto x o viceversa (a seconda dell'ordine dei tempi); donde il nome di propagatore. In modo analogo, si considera la G(x, y) come un'ampiezza di probabilità per la propagazione di un elettrone da y a x (se x⁰ > y⁰) o, rispettivamente, di un positone da x a y (se y⁰ > x⁰). Questo procedimento si può giustificare esaminando in maggior dettaglio la decomposizione dei campi ψ e ψ* in una parte di ‛creazione' e in una di ‛assorbimento', ripetendo però l'avvertimento che queste interpretazioni intuitive non si riferiscono a reali esperimenti e non vanno prese troppo alla lettera.

Funzioni di Green più complicate sono la funzione di tre punti x, y, z che si ottiene considerando un prodotto ‛misto' di due campi di Dirac, ψ(x) e ψ*(y), e di un campo A_μ(z); altri prodotti di tre campi che diano un valor medio non nullo non esistono. Una funzione di Green di quattro punti x, y, z, w, che è anche un tensore a quattro indici, è definita (se x⁰ > y⁰ > z⁰ > w⁰) dal valor medio

D_αβγδ(x, y, z, w)) = 〈∣ A_α(x) A_β(y) A_γ(z) A_δ(w)∣> (11)

e dalla regola dell'ordine cronologico negli altri casi. Similmente si definisce una funzione di quattro punti G (x, y, z, w) mediante un prodotto di due fattori ψ e due ψ*; essa possiede quattro indici spinoriali, che omettiamo. Anche per queste funzioni è possibile dare un'interpretazione intuitiva come sopra: esse danno le ampiezze di probabilità per l'osservazione di due particelle nei punti x e y, nell'ipotesi che due particelle analoghe siano state precedentemente create nei punti z e w. Nel caso della funzione D si tratta di due fotoni, in quello della G di due elettroni (o anche, con un'opportuna permutazione delle variabili, di due positoni, o di un elettrone e un positone).

Senza entrare in dettagli, illustriamo brevemente come si possano calcolare funzioni più complicate di quelle finora prese in considerazione, evidenziandone il significato fisico e le relazioni con la matrice S. Per non appesantire il discorso e le formule, ometteremo spesso gli indici di Dirac o gli indici tensoriali, o gli uni e gli altri. Ricordando la distinzione già fatta tra valori in approssimazione zero e valori esatti, indicheremo con D⁰ e con G⁰ le funzioni di Green di due punti in approssimazione zero (per esempio la 10, in cui a secondo membro sia posto un valor medio 〈...>₀). Senza dare la forma esplicita del risultato, possiamo caratterizzarlo sufficientemente dicendo che la D⁰ è un nucleo risolvente (ossia una funzione di Green nel senso usuale della fisica matematica) dell'equazione delle onde di D'Alembert inomogenea;

□f(x) = g(x).

In altre parole, se indichiamo simbolicamente con g → D⁰g l'operazione integrale lineare

g(x) → ∫ D⁰(x, y) g(y) (dy), (12)

possiamo dire che l'operatore D⁰ è un inverso, □^-1, dell'operatore di D'Alembert. In modo simile, se scriviamo l'equazione di Dirac omogenea nella forma Dψ = 0, possiamo dire che la G⁰(x, y) definisce un operatore G⁰ che è un inverso, D^-1 dell'operatore differenziale di Dirac.

L'importanza particolare di queste due funzioni deriva dal fatto che esse sono precisamente le espressioni rappresentate simbolicamente nei diagrammi di Feynman dalle linee interne di fotone e, rispettivamente, di elettrone (v. fig. 4). La freccia, che è parte integrante del simbolo che indica G⁰(x, y), non è necessaria nel caso della D⁰, per via della simmetria di quest'ultima funzione. Per completare le regole di Feynman basta dare i coefficienti γμ_ρσ, che indicano in che modo vadano accoppiati gli indici vettoriali e spinoriali (che abbiamo omesso) delle D⁰ e G⁰ che hanno un vertice in comune, e indicare in modo più preciso quali siano i diagrammi ammessi per un dato elemento della matrice S. Sarà bene avvertire sin d'ora che le regole non esauriscono il problema; la difficoltà principale sta nelle integrazioni (rispetto ai vertici) che vengono prescritte dalle regole.

Anche il calcolo delle approssimazioni superiori per una qualsiasi funzione di Green si riduce in sostanza allo stesso formalismo, ossia al calcolo di espressioni specificate da diagrammi di Feynman, che differiscono da quelli usati nel calcolo della matrice d'urto solo per un particolare: al posto delle linee esterne (che non rappresentano un propagatore) subentrano linee interne, che collegano, in generale, un vertice con uno dei punti x, y, ... che sono le variabili della funzione di Green. Possiamo chiamare questi punti ‛vertici esterni'. Per comprendere questa differenza, consideriamo il calcolo della funzione di Green definita dalla (11). All'ordine zero, la funzione è data dalla somma di tre prodotti, che corrispondono ai tre diversi modi di accoppiare i quattro campi A:

questo risultato è rappresentato dai tre diagrammi, A, B, C, della fig. 5. Ognuno dei termini rappresenta la propagazione indipendente di due fotoni, com'era facile prevedere. I primi diagrammi interessanti sono sei diagrammi del tipo di quello riprodotto nella fig. 6 (altri 5 si ottengono permutando gli indici x, ..., w). Questi diagrammi rappresentano l'interazione tra due fotoni, attraverso una creazione virtuale di coppie elettrone-positone (v. anche la discussione relativa alla fig. 7o in particelle elementari: Campi e particelle).

Supponiamo ora di studiare il comportamento asintotico della funzione quando i punti x, y, ... tendono all'infinito; si dimostra che il risultato è quello che viene suggerito dall'intuizione fisica. Il termine principale dello sviluppo asintotico descrive in sostanza, secondo il formalismo della meccanica ondulatoria, due fotoni che, provenendo dall'infinito con la velocità della luce, interagiscono per un certo tempo, per poi allontanarsi di nuovo in direzioni diverse sempre alla stessa velocità; l'elemento della matrice S che descrive l'urto tra due fotoni viene così messo in relazione diretta con il comportamento asintotico della corrispondente funzione di Green. Questo avviene beninteso anche per gli altri elementi della matrice S; simbolicamente, quando i vertici esterni x, y, ... vanno all'infinito, le linee ad essi collegate diventano linee esterne e ciò implica una diversa prescrizione riguardo al fattore che rappresentano.

Vediamo ora i principali problemi che si incontrano nell'eseguire i calcoli prescritti dalle regole. Se il diagramma è semplicemente connesso (v. cap. 1), tutte le integrazioni si possono eseguire ricorrendo alla rappresentazione di Fourier dei propagatori e ci si riduce così a calcoli puramente algebrici. Se il diagramma contiene circuiti chiusi, il metodo richiede ulteriori integrazioni sullo ‛spazio dei momenti', che per di più danno in generale un risultato divergente; questa difficoltà non dipende dal metodo usato. Per esempio: lo sviluppo perturbativo dei propagatori D(x, y) e G(x, y) comincia con i termini d'ordine zero D⁰ e, rispettivamente, G⁰ e prosegue con termini di ordine a rappresentati dai diagrammi della fig. 7. L'espressione corrispondente alla ‛bolla', posta al centro di questi diagrammi, omettendo i soliti coefficienti inessenziali, è il prodotto di due propagatori d'ordine zero: G⁰(z, w) G⁰(w, z), nel primo caso, e G⁰(z, w) D⁰(w, z), nel secondo. Occorre precisare che questi fattori sono, per ragioni abbastanza ovvie, funzioni soltanto della differenza z - w tra le coordinate dei due punti e inoltre, come è noto dallo studio delle funzioni di Green della fisica matematica, sono funzioni singolari, che diventano cioè infinite quando si annulla la distanza relativistica tra i punti z e w (singolarità sul ‛cono di luce'). Bisogna poi aggiungere che, mentre questa singolarità non è tale da impedire che gli integrali come quello a secondo membro della (12) abbiano un senso, purché la funzione g sia sufficientemente regolare (cosa anche questa ben nota dalla fisica matematica), nei due prodotti G⁰G⁰ e G⁰D⁰ sopracitati il sovrapporsi delle singolarità dei due fattori priva di significato l'integrazione rispetto ai vertici z e w, richiesta dalle regole.

La portata generale di questa difficoltà risulta dalla considerazione seguente. Se una qualsiasi funzione di Green o un qualsiasi elemento della matrice S corrispondente a un dato processo sono dati all'ordine più basso da un diagramma ad albero, le cui linee interne rappresentano fattori D⁰ oppure G⁰, agli ordini superiori compariranno certamente diagrammi che si ottengono dal primo inserendo nelle linee interne una ‛bolla' simile a quelle della fig. 7 a seconda della natura elettronica o fotonica del propagatore in questione. Le integrazioni corrispondenti a questi diagrammi saranno allora divergenti. Se a questo si aggiunge la divergenza associata al diagramma triangolare della fig. 8, si può dire (semplificando un poco) che la presenza, entro un diagramma, di parti simili a quelle ora esaminate rappresenta la condizione necessaria e sufficiente perché il risultato sia divergente.

4. La rinormalizzazione: confronto con l'esperienza e significato fisico dei risultati.

L'analisi generale delle divergenze, dovuta a Dyson, circoscrive il problema nel modo che ci apprestiamo a illustrare. La rinormalizzazione trasforma poi le espressioni divergenti in altre che hanno un valore ben definito.

Notiamo anzitutto che il primo diagramma della fig. 7 è lo stesso che compare nel calcolo della polarizzazione del vuoto (v. anche particelle elementari: Campi e particelle, fig. 7M); si tratta infatti solo di due diverse facce dello stesso problema. Il nucleo Π dell'eq. (9) si presenta dunque a tutta prima sotto la forma del prodotto singolare G⁰G⁰ già incontrato. Si può tuttavia mostrare, seguendo una linea di ragionamento già indicata da Dirac nel 1934, che l'integrale divergente che dà la polarizzazione del vuoto è separabile formalmente in due parti, una delle quali, e precisamente la ‛parte finita' che compare nell'equazione (9), è convergente, l'altra, della forma kaJ, in cui k è una costante di proporzionalità data da un integrale sullo spazio dei momenti (si tratta del momento di una delle particelle virtuali della coppia rappresentata dalla ‛bolla' nel primo diagramma 7), è divergente. Che diritto abbiamo di omettere questo scomodo termine privo di senso? Rispondiamo, provvisoriamente, che esso non viene realmente omesso, ma viene piuttosto associato all'originaria corrente esterna, che diventa così la corrente esterna ‛rinormalizzata' J_r = (1 + ak) J o, per essere più esatti, un'espressione che include anche l'effetto degli ordini superiori α² α³ ecc Se Q = ∫ J⁰ d³x è la carica totale esterna considera'ta iniÀalmente, il valore rinormalizzato della carica sarà ora Q_r = (1 + αk + ...) Q. Si dimostra poi che lo stesso fattore di rinormalizzazione, compare nelle formule anche accanto alla carica e dell'elettrone; in altre parole, ogni carica viene moltiplicata per lo stesso fattore. La ‛rinormalizzazione della carica' si effettua esprimendo i risultati del calcolo (ampiezze o sezioni d'urto, livelli energetici, ecc.) in funzione delle cariche rinormalizzate Q_r, ed e_r invece che di quelle inizialmente introdotte nelle equazioni del moto.

Dal punto di vista fisico queste manipolazioni si possono giustificare come un metodo euristico per scoprire quali sarebbero i risultati di una teoria ‛finita', ma sostanzialmente identica a quella attuale per quel che riguarda le basse energie; questa teoria dovrebbe cioè differire da quella qui descritta in quanto eliminerebbe le divergenze dovute a integrazioni sugli stati virtuali, senza per altro modificare sostanzialmente quei risultati che sono ampiamente verificati dall'esperienza. Un'indicazione incoraggiante in questo senso è data dai risultati del cosiddetto metodo del ‛taglio' nello spazio dei momenti. Questo metodo, sia pur grossolano, suggerisce che le correzioni radiative saranno di un ordine di grandezza del tutto compatibile coll'esperienza, a meno che per il taglio K (∣k∣ 〈 K è la sfera di integrazione) non si assumano valori estremamente grandi. La costante L che determina la rinormalizzazione della carica risulta infatti dell'ordine del log(K/mc), che cresce assai lentamente al crescere di K. È quindi ragionevole considerare αL come una correzione del primo ordine in α, anche se a rigore, nel limite K → ∞, la correzione diverge.

Risultati del tutto analoghi si ottengono per la ‛rinormalizzazione della massa', ossia per la variazione δm che la massa dell'elettrone subisce, a causa della sua interazione col campo da esso stesso creato (v. anche particelle elementari: Campi e particelle). Questo effetto, già noto dalla teoria classica (Lorentz), non è poi altro, nella teoria quantistica, che il summenzionato spostamento dei livelli per il caso di un elettrone libero allo stato di riposo. Il metodo del taglio applicato alla teoria del campo elettrone-positone di Dirac dà per questo effetto un valore dell'ordine δm = αmL′, dove L′ è una costante logaritmicamente divergente analoga alla L di cui sopra (Weisskopl, 1937). A noi qui interessa indicare come questo effetto si presenti nel forma: lismo perturbativo invariante delle funzioni di Green. E chiaro che la variazione δm della massa deve essere uno degli effetti che determinano la differenza tra il propagatore G(x, y) dell'elettrone e il suo valore in approssimazione zero: G⁰(x, y). Questa differenza è data da una serie, che nella notazione simbolica (cfr. l'osservazione a seguito dell'eq. 12) si può scrivere:

G − G⁰ = αG⁰MG⁰ + ..., (14)

dove il primo termine a destra corrisponde al primo diagramma della fig. 7 e quelli successivi, di ordine α², α³, a diagrammi più complicati. Il fattore M, anch'esso un operatore, rappresenta il nucleo M(z, w) corrispondente alla bolla centrale del secondo diagramma della fig. 7. Poiché δm e' divergente, nel limite K → ∞, non sorprende che il secondo diagramma della fig. 7 dia un risultato divergente.

Supponiamo per un momento che la differenza tra G e G⁰ sia dovuta interamente alla variazione della massa, ossia che G si possa calcolare sostituendo, in G⁰, al valore m della massa un opportuno valore rinormalizzato m_r m + δm. Notiamo che la relazione tra due operatori di Dirac corrispondenti a due diversi valori della massa è semplicemente D_m+δm = D_m − δm. (Usiamo qui la forma

quale si ottiene dall'equazione di Dirac, riportata in quanti, teoria dei: Meccanica quantistica, cap. 6, È b, moltiplicandola a sinistra per la matrice β, ponendo c = 1, ℏ = 1 e sulla base della relazione β² = 1). La corrispondente relazione tra G e G⁰ sarebbe allora:

Ora, tenendo presente che δm è del primo ordine in α, nel senso sopra spiegato, e sviluppando in potenze di α, possiamo scrivere:

G = (l + G⁰ δm + ...)G⁰, (14b)

che coinciderebbe proprio con la (14), se l'operatore αM si potesse identificare con la costante moltiplicativa δm.

Come già nel caso dell'operatore di polarizzazione Π, l'operatore M non è in realtà ben definito, ma la sua struttura si può analizzare applicando la trasformazione di Fourier al corrispondente nucleo singolare M(z, w). In modo analogo a quanto avviene per Π, si trova che αM si può decomporre in una parte divergente e una parte finita, che è trascurabile nel caso della propagazione di un elettrone libero. La parte divergente consta di due termini della forma c₁ 1 + c₂D, dove c₁ e c₂ sono costanti proporzionali ad α e date da integrali logaritmicamente divergenti come quelli già incontrati. Più precisamente la c₁ è proprio, come vuole la (14a), la stessa espressione già utilizzata da Weisskopf per la correzione radiativa δm della massa. La costante c₂ rappresenta a sua volta soltanto una rinormalizzazione dell'intero propagatore e scompare dai risultati quando viene combinata con una divergenza del tutto simile, che compare nel diagramma triangolare della fig. 8. In conclusione, ricordando quanto si è detto per la costante L, tutte le divergenze possono venire ‛assorbite' mediante la rinormalizzazione della carica e della massa, ossia esprimendo le quantità calcolate in funzione delle cariche Q_r e della massa m_r. Infine, manipolazioni del tutto simili, anche se più complicate, sono possibili agli ordini superiori in α, portando così, ordine per ordine, a una completa eliminazione delle divergenze.

Abbiamo così descritto, molto sommariamente, i metodi e le idee che hanno consentito il calcolo delle correzioni radiative dell'elettrodinamica quantistica, in particolare quelle elencate nella tab. Il, cui ci riferiremo in seguito. Il significato e l'importanza di quanto è stato fatto emergono da un esame più dettagliato dei risultati.

Notiamo anzitutto come il calcolo, talvolta assai pesante, degli effetti di ordine superiore (in α¹ e anche α³) sia importante non soltanto in linea di principio: la precisione dei risultati sperimentali consente spesso la verifica delle previsioni.

Il caso più elegante ci è offerto dal momento magnetico anomalo dell'elettrone (e del muone). L'anomalia α è misurata dalla deviazione del fattore ‛giromagnetico' g di Landé dal suo valore ‛normale' g = 2 (valore sul quale teoria ed esperienza collimavano sino al 1947). Scrivendo g = 2(1 + a) le esperienze più precise danno per a i valori:

per l'elettrone e il muone, rispettivamente. Per le stesse grandezze la teoria (v. anche tab. Il, effetto 4) dà uno sviluppo in serie:

Il termine del primo ordine in α corrisponde alla correzione del vertice rappresentata dal diagramma della fig. 8, qualora alla linea fotonica esterna si assegni il valore corrispondente a un campo magnetico omogeneo esterno. Il calcolo è identico per le due particelle e il valore è indipendente dalla massa; per questo motivo i due valori dell'eq. (15) sono così vicini tra loro. La piccola differenza è però significativa (circa 20 volte l'errore sperimentale attuale; ma sono in corso esperienze ancora più precise). Essa è inoltre teoricamente assai interessante. La differenza prevista dalla teoria è dovuta in gran parte al termine in a², al quale contribuiscono ben 8 diagrammi, 7 dei quali danno un contributo indipendente dalla massa, ossia lo stesso contributo ad a_e e a_μ (conclusione cui si giunge del resto, senza calcoli, dalla semplice ispezione degli integrali). L'ottavo diagramma (v. fig. 9A) si ottiene dal diagramma della fig. 8 inserendo nella linea fotonica interna una bolla di polarizzazione del vuoto (v. fig. 7) corrispondente alla creazione di coppie di massa ‛diversa' da quella esterna (beninteso, si dovrebbe anche considerare la possibile creazione di coppie di mesoni π o di altri adroni. Questi effetti, la cui valutazione è soggetta alle incertezze cui si è accennato nell'introduzione, sono certamente piccolissimi nel caso dell'elettrone e abbastanza piccoli in quello del muone). Il diagramma della fig. 9B, in cui la massa è la stessa nella linea esterna e nella bolla, è uno dei 7 diagrammi indipendenti dalla massa. Mentre il diagramma della fig. 9A dà un contributo importante ad a_μ, il diagramma corrispondente per gli elettroni dà un contributo del tutto trascurabile: la polarizzazione del vuoto dovuta ai muoni modifica il propagatore D dei fotoni solo per momenti troppo grandi per influire sul valore del triangolo. L'esistenza di questo curioso effetto è completamente confermata dalle misure (v. eq. 15). Si noti ancora che, particolarmente nel caso del valore assai preciso di a_e, il confronto completo con l'esperienza è stato possibile solo grazie al laboriosissimo calcolo dei 72 diagrammi del terzo ordine.

Notiamo infine come in tutti questi confronti sia necessario usare un valore assai preciso della costante di struttura fine α. La determinazione di questa costante è stata notevolmente facilitata dalla scoperta dell'effetto Josephson (v. criofisica), ma nella media pesata oggi considerata come il valore più attendibile intervengono anche misure di struttura fine e simili, alla cui valutazione la teoria ha contribuito in modo assai utile.

Passando allo spostamento dei livelli (effetto Lamb), anche qui si ha un'interessante differenza tra gli ordinari livelli elettronici e i livelli di un muone in atomi mesici (v. atomo). Nel primo caso, il più noto, il termine principale è ancora dato dalla correzione al vertice (v. fig. 8), nel quale ora la linea fotonica esterna rappresenta il campo coulombiano dovuto al nucleo dell'atomo. Circa il significato fisico di questo termine, si noti che esso rappresenta simbolicamente gli effetti già discussi con altro linguaggio all'inizio del cap. 3 (Si veda anche la discussione in particelle elementari: Campi e particelle) e si ricordi anche quanto è stato ivi detto circa l'ordine di grandezza del termine. Notiamo poi che un termine meno importante, ma dello stesso ordine in α, è dato dalla polarizzazione del vuoto (v. anche tab. Il, effetto 3). Si tratta qui d'inserire la bolla della fig. 7 nella linea che rappresenta il campo esterno. Nel caso dell'anomalia abbiamo potuto ignorare questo diagramma, essendo nullo il suo contributo. Nel caso dell'effetto Lamb, il contributo è piccolo (esso fu perfino messo in dubbio, prima della precisa conferma sperimentale), ma assai significativo per una valutazione generale della validità della teoria. A questo proposito, si deve considerare come promettente lo studio degli atomi mesici. La summenzionata differenza tra i livelli di un elettrone e quelli corrispondenti per un muone (in particolare la notevole differenza tra le dimensioni dell'orbita nei due casi) fa sì che per i muoni la polarizzazione del vuoto sia un effetto assai più importante della correzione del vertice della fig. 8. Anche qui, come nel caso della fig. 9, gioca il fatto che la polarizzazione del vuoto è dovuta soprattutto agli elettroni. La piccolezza del raggio di Bohr per il muone fa sì che esso penetri facilmente nella regione in cui la polarizzazione del vuoto si fa sentire.

Naturalmente, nello spostamento di Lamb, oltre alle correzioni di ordine α sinora considerate, intervengono anche effetti di ordine superiore, come, tra gli altri, quello della fig. 9. (Ricordiamo ancora una volta che, in questi effetti che riguardano elettroni legati, l'ordine in α del diagramma non dà tutti i fattori che in realtà intervengono nel determinare l'ordine di grandezza dell'effetto). Per una discussione di questi effetti più fini, come di numerose altre applicazioni dei metodi descritti al calcolo della struttura fine o iperfine dei livelli di vari sistemi si vedano i compendi citati nella bibliografia. Similmente rimandiamo il lettore all'articolo particelle elemetari, per ulteriori considerazioni sul significato generale dei risultati ottenuti e sulle probabili limitazioni della teoria attuale.

Bibliografia.

Brodsky, S. J., Drell, S. D., The present status of quantum electrodynamics, in ‟Annual reviews of nuclear science", 1970, XX, pp. 147 ss.

Fermi, E., Quantum theory of radiation, in ‟Reviews of modern physics", 1932, IV, pp. 87-132.

Hughes, V. W., Status of QED experiments, in Atomic physics, London 1973.

Kroll, N. M., Status of QED theory, in Atomic physics, London 1973.

Lautrup, B. E., Peterman, A., Rafael, E. de, Recent developments in the comparison between theory and experiments in quantum electrodynamics, in ‟Physics reports", 1972, III, pp. 193-260.

Schwinger, J. S. (a cura di), Quantum electrodynamics, New York 1958.