Controllo, teoria del
Controllo, teoria del
La t. del c. studia i metodi per capire, governare e modificare il comportamento di sistemi dinamici, naturali o artificiali, al fine di guidarli a raggiungere finalità assegnate. Per sistema dinamico si intende un insieme di grandezze variabili nel tempo in modo interdipendente. I sistemi dinamici oggetto della t. del c. possono essere di natura diversa: essi sono in molti casi sistemi fisici elementari (per es., meccanici, elettrici, termodinamici), ma vi sono anche sistemi di natura biologica, economico-finanziaria, ecologica e ambientale. Spesso, in un sistema controllato convivono e interagiscono elementi differenti, in particolare le grandezze fisiche del sistema da controllare, e le informazioni usate dalla logica del controllo.
La t. del c. riesce ad affrontare in modo generale e unificato problemi così diversi e complessi grazie soprattutto all'utilizzo di metodi e modelli matematici, che consentono di valutare quantitativamente e obiettivamente le proprietà dei sistemi e di progettare sistematicamente le tecniche per correggerli. È d'altronde vero che non tutti, anzi solo pochissimi dei sistemi fisici trattati, ammettono descrizioni matematiche di soddisfacente precisione: la t. del c. tratta perlopiù modelli matematici approssimati di sistemi reali. È quindi una caratteristica essenziale della t. del c. l'attenzione alla robustezza dei metodi, vale a dire a quanto i risultati dello studio su modelli approssimati rimangono validi rispetto ai sistemi e alle condizioni reali.
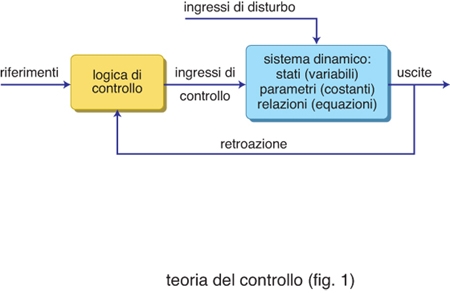
Gli elementi fondamentali di un sistema dinamico controllato sono descritti in figura. Essi sono relativamente pochi, e la loro comprensione è immediata se ci si riferisce a un semplice esempio, che si utilizzerà a più riprese a scopo illustrativo nel corso della trattazione. Si pensi dunque al problema di regolare la velocità di crociera di un autoveicolo che procede lungo una strada incontrando condizioni variabili, in modo da mantenere la velocità stessa vicina a determinati valori di riferimento che il conducente imposta secondo le sue diverse necessità. Tradizionalmente è il conducente stesso ad agire sul pedale dell'acceleratore sulla base della velocità del veicolo letta dal tachimetro; le stesse funzioni possono essere svolte da un sistema di controllo automatico (quali i cosiddetti sistemi cruise control che si trovano ormai frequentemente nei moderni autoveicoli), ottenendo prestazioni migliori e sollevando il pilota da un compito alla lunga faticoso.
Il sistema fisico da controllare in questo esempio è caratterizzato dalla massa inerziale del veicolo, dalle sue proprietà aerodinamiche, dagli attriti delle trasmissioni e dei pneumatici, dalla pendenza della strada ecc.. Tutte queste grandezze sono parametri che influenzano la dinamica del sistema, espressa mediante le equazioni del moto del veicolo, ossia le equazioni differenziali che legano l'accelerazione, la velocità e la posizione del veicolo alla spinta che il motore produce.
Tra le grandezze che appaiono nelle equazioni dinamiche del sistema, è naturale riconoscere ad alcune un ruolo particolare. La spinta del motore può essere considerata una variabile indipendente, manovrabile a piacimento (seppure entro dati limiti) modulando l'alimentazione del carburante al motore. Questa variabile, che è causa delle variazioni delle altre grandezze, è detta ingresso di controllo per il sistema, ed è sovente collegata a un dispositivo attuatore in grado di eseguire le manovre desiderate (nel caso in esame potrebbe essere un piccolo motore elettrico che apre e chiude la valvola di alimentazione). Altre variabili indipendenti, che non sono gestibili, ma possono opporsi alle finalità del controllo (per es., la spinta contraria del vento sul veicolo) sono invece dette ingressi di disturbo.
Le grandezze che variano nel tempo in modo dipendente dagli ingressi (per es., la posizione del veicolo lungo la strada e la sua velocità) sono dette variabili di stato (o stati) del sistema. Una descrizione dello stato di un sistema consiste nell'assegnare valori a un numero sufficiente di tali variabili, in modo che tutta l'evoluzione del sistema possa essere determinata univocamente con la sola conoscenza degli ingressi. Questa definizione ha naturalmente valore teorico: infatti, è impossibile in pratica conoscere esattamente a priori gli ingressi (in particolar modo, i disturbi) che saranno applicati, e la vera dinamica del sistema. In generale, poi, non è possibile conoscere direttamente il valore delle variabili di stato, eccetto che per alcune loro combinazioni, che possono essere misurate da opportuni sensori: tali grandezze sono dette uscite del sistema. La grandezza la cui regolazione è l'oggetto principale del controllo (la velocità del veicolo, nell'esempio) è in particolare detta uscita di riferimento del sistema.
Lo scopo del controllo è in generale quello di utilizzare gli ingressi disponibili per regolare le uscite in accordo a valori di riferimento assegnati, a dispetto dei possibili disturbi. Ciò può essere ottenuto scegliendo il controllo sulla base delle informazioni disponibili, che sono fondamentalmente di due tipi: la conoscenza del modello dinamico e la misurazione delle uscite del sistema. Il primo tipo d'informazione permette di prevedere gli effetti che diversi ingressi di controllo avrebbero sul sistema, e quindi, in certa misura, di impostarli in modo da prefigurarne un corretto comportamento. Nel controllo di crociera, per es., si tratterebbe di calcolare quali resistenze sarebbero incontrate dal veicolo alla velocità desiderata nel tratto di strada da affrontare, e quale spinta dovrebbe essere applicata dal motore per vincerle. Questo tipo d'azione di controllo è detta in avanti (feedforward) oppure in anello aperto.
Il secondo tipo di controllo basa invece la scelta degli ingressi sulla misurazione continua dei valori di uscita e sul loro confronto istante per istante con gli andamenti desiderati: per es., se la velocità del veicolo è inferiore al valore di riferimento impostato, la spinta del motore potrebbe essere aumentata, oppure ridotta nel caso opposto, di una quantità tanto maggiore quanto maggiore è lo scarto. Questo tipo di azione di controllo viene detta in retroazione (feedback) oppure in anello chiuso.
Le differenze tra le due strategie sono evidenti: mentre l'efficacia dell'azione in avanti dipende fortemente dalla qualità delle informazioni sul modello del sistema e sui disturbi, la retroazione può in buona parte prescinderne, basandosi principalmente sulla qualità dei sensori utilizzati. La retroazione è il meccanismo alla base del funzionamento di moltissimi sistemi, sia naturali sia artificiali. D'altronde, anche l'efficacia del controllo in retroazione è limitata da vari fattori, tra i quali la stabilità del sistema controllato e la sua sensibilità alle imprecisioni casuali (rumore) e ai ritardi delle misure. Una delle problematiche principali della t. del c. è quella di fornire il migliore compromesso nell'utilizzo delle due strategie.
I sistemi dinamici sono solitamente controllati per agire in condizioni vicine a condizioni nominali, nelle quali il loro comportamento è migliore. Una condizione di funzionamento nominale, che spesso è uno stato di equilibrio per il sistema, si dice stabile se il sistema, quando si trovi a operare in condizioni leggermente perturbate, continua a evolvere senza allontanarsi troppo dalla condizione nominale; si dice poi asintoticamente stabile se tale scostamento è annullato nel tempo. Queste nozioni di stabilità, dette di Lyapunov, dal nome del matematico russo che le ha rigorosamente definite e studiate, si riferiscono a perturbazioni degli stati del sistema: nell'esempio dell'autoveicolo, se vi è un leggero aumento della velocità mentre ogni altro parametro e ingresso è mantenuto costante, il corrispondente aumento della resistenza aerodinamica tende a frenare il veicolo, dando stabilità alla condizione precedente la perturbazione. Altrettanto importanti sono differenti nozioni di stabilità riferite a variazioni dei parametri o della struttura del modello (stabilità strutturale, assoluta o totale) o alla limitatezza delle variazioni delle uscite corrispondenti a limitate variazioni degli ingressi. Nell'esempio, un cambiamento di pendenza della strada provoca una variazione della velocità di crociera che non è riassorbita dal sistema se non modificando la spinta del motore.
La stabilità è una delle principali specifiche richieste al funzionamento di un sistema controllato, spesso quantificata in termini di rapidità di recupero delle condizioni nominali. Il controllo in retroazione influenza profondamente la stabilità, potendo sia rendere stabile e veloce un sistema che non lo è abbastanza di per sé (come nell'esempio del cruise control), sia, all'opposto, rendere instabile un sistema che in assenza di retroazione sarebbe stabile. Il ritardo che può intercorrere tra l'istante in cui si ha un valore d'uscita e l'effettiva applicazione della retroazione corrispondente può causare questa instabilità: ne è un esempio quotidiano e macroscopico la difficoltà con la quale regoliamo la temperatura di un getto d'acqua da un rubinetto, quando, a causa di un impianto idraulico non ben progettato, si ha un consistente ritardo tra l'azione sul miscelatore e l'effettiva variazione di temperatura dell'acqua. I ritardi di misura e/o di attuazione in un sistema sono legati alle tecnologie adottate, e spesso sono economicamente irriducibili: la loro presenza costringe a un uso accorto della retroazione, il cui progetto richiede tecniche matematiche anche sofisticate.
La t. del c. ebbe un fortissimo sviluppo negli anni intorno alla Seconda guerra mondiale, contribuendo alla realizzazione di nuovi sistemi avanzati di pilotaggio per navi e aerei, di puntamento d'arma e di telecomunicazione. Lo sviluppo dell'elettronica negli anni Quaranta e Cinquanta del 20° sec. richiese tecniche più avanzate di stabilizzazione in retroazione, per es., per i nuovi amplificatori ad alte prestazioni che furono resi possibili dai primi transistor. In questa fase storica crebbero fortemente le tecniche di analisi e sintesi del controllo nel dominio della frequenza, basate sulle trasformate dei segnali e sull'analisi delle risposte dei sistemi a ingressi sinusoidali (analisi armonica). Si ebbe in quegli anni lo sviluppo di concetti, quali quello di funzione di trasferimento, che, rappresentando in modo completo e compatto il rapporto tra l'ingresso e l'uscita di un sistema dinamico lineare, permisero di descrivere e analizzare complesse interconnessioni tra sottosistemi. Si definirono tecniche analitiche o grafiche, quali il criterio di stabilità di H. Nyquist per la stabilità dei sistemi in retroazione o le tecniche di sintesi basate sui diagrammi e sulle relazioni integrali di H.W. Bode per ottenere sistemi di controllo con specifiche assegnate di stabilità e di prestazioni. Molti dei fondamentali contributi di questo periodo sono ancora alla base della progettazione di gran parte tra i più semplici schemi di controllo adottati nell'industria, tra i quali il più noto e diffuso è il cosiddetto controllo PID (proporzionale, integrale, derivativo). Nello stesso periodo, la t. del c. si aprì anche a orizzonti più vasti, abbracciando la teoria della probabilità e dei sistemi stocastici, e unificando nell'ambizioso programma della cibernetica di N. Wiener lo studio della comunicazione e del controllo negli esseri animati e nelle macchine.
Un secondo balzo in avanti della t. del c. avvenne negli anni Sessanta del 20° sec., in coincidenza con lo sviluppo tecnologico stimolato dalla competizione tra il blocco occidentale e quello sovietico in ambito aerospaziale. Si assistette in quegli anni a un progresso eccezionale in molte diverse direzioni di studio. La ripresa e l'estensione dei risultati di Lyapunov permisero di affrontare lo studio della stabilità di sistemi con elementi non lineari. L'estensione dei metodi del calcolo delle variazioni a sistemi soggetti a vincoli sugli ingressi generò la teoria del controllo ottimo, sviluppata quasi contemporaneamente e con approcci diversi da L.S. Pontryagin in Unione Sovietica e da R. Bellmann negli Stati Uniti. Il controllo ottimo può dare preziose indicazioni sui segnali d'ingresso da usarsi per far raggiungere a un sistema desiderate configurazioni finali, ottimizzando la prestazione e minimizzando i costi connessi alla sua attuazione: un'esemplare applicazione è il controllo del vettore di un satellite artificiale tra il lancio e la messa in orbita, dove la riduzione del carburante necessario ha ovvio impatto sulla massa da lanciare.
La t. del c. sviluppata negli anni Sessanta del 20° sec. poneva l'accento prevalentemente su tecniche nel dominio del tempo dei sistemi, rappresentati direttamente nello spazio degli stati dalle rispettive equazioni dinamiche. Grazie all'applicazione e allo sviluppo di una matematica piuttosto avanzata (usando principalmente strumenti di analisi e algebra lineare), fu possibile raggiungere una soddisfacente comprensione di questioni teoriche fondamentali, quali la controllabilità e l'osservabilità dei sistemi lineari. Il primo concetto è relativo all'effettiva possibilità di guidare un sistema, mediante i suoi ingressi, ad assumere condizioni arbitrarie; il secondo si riferisce alla possibilità di conoscere l'intero stato di un sistema, potendo solo accedere alla misura di alcune grandezze di uscita.
Il problema della sintesi di un controllore (o regolatore) per un sistema lineare, ottimo rispetto a indici di prestazione e costi di attuazione quadratici, o sintesi LQR (Linear Quadratic Regulator), fu risolto brillantemente, così come venne risolto il problema della stima ottima degli stati ignoti di un sistema mediante filtraggio delle misure di uscite affette da rumore gaussiano (filtro ottimo o di Kalman). Il cosiddetto teorema di separazione dimostrò che il sistema ottenuto connettendo un regolatore e un filtro, progettati indipendentemente in modo ottimo, ottiene ancora prestazioni globalmente ottime, mettendo in tal modo a disposizione una potentissima e sistematica tecnica di sintesi di sistemi di controllo, detta sintesi LQG (Linear Quadratic Gaussian Regulator).
Il grande impulso teorico degli anni Sessanta mise a disposizione una ricchezza di risultati che, insieme alla disponibilità di mezzi di calcolo elettronico adeguati, rese possibili, verso la fine degli anni Settanta e nei primi anni Ottanta, molte applicazioni dei controlli automatici a sistemi di complessità che prima era impensabile considerare. Dalle applicazioni pratiche di quelle teorie ne furono peraltro evidenziate alcune limitazioni: in particolare, si riscontrò in certi casi che le soluzioni fornite non possedevano la necessaria robustezza rispetto alle inesattezze del modello e alla presenza di disturbi. Lo studio accurato di condizioni sotto le quali la stabilità e le prestazioni del sistema controllato potevano essere garantite in modo robusto e affidabile, reso necessario dalle esigenze di sicurezza in applicazioni di grande responsabilità, rivelò che il problema può essere decisamente complesso. Le tecniche in frequenza tornarono a essere attentamente considerate, per la loro migliore capacità di catturare gli aspetti di robustezza; si ricorse ad adatte teorie matematiche (quali l'analisi funzionale) e si svilupparono nuove teorie e tecniche di controllo robusto, quali, per es., il controllo H∞ (H-infinito). La complessità della soluzione dei problemi del controllo robusto stimolò l'attenzione verso tecniche numeriche efficienti e accurate per la progettazione assistita da calcolatore dei sistemi di controllo (CACSD, Computer-Aided Control System Design).
Sempre a partire dagli anni Ottanta del 20° sec., la possibilità offerta dai nuovi processori elettronici di calcolare leggi di controllo sofisticate in pochi millisecondi aprì la porta a un approccio più ambizioso verso i sistemi non lineari, non più basato su locali approssimazioni lineari ma su tecniche esatte valide in campi più ampi. Utilizzando risultati matematici di geometria differenziale e di analisi dei sistemi dinamici, e sviluppandone di nuovi, si poterono affrontare problemi quali, per es., lo studio della controllabilità e della osservabilità dei sistemi non lineari, e la loro esatta trasformazione in sistemi lineari mediante retroazione. Uno dei problemi più stimolanti che la t. del c. ha affrontato è quello di controllare sistemi di cui non si conoscano, completamente o in parte, i modelli. In modo figurato, si può pensare al problema che si porrebbe di fronte alla richiesta di guidare un veicolo i cui comandi sono ignoti, o noti soltanto in parte. L'osservazione delle risposte fornite dalle uscite del sistema in corrispondenza a ingressi noti può fornire dati empirici essenziali per la costruzione di un modello, ciò può essere fatto utilizzando opportune tecniche di identificazione dei sistemi. La t. del c. ha dedicato grande attenzione ai problemi di identificazione, utilizzando e sviluppando nuovi risultati con approcci diversi: statistici, di analisi funzionale, di apprendimento e generalizzazione (machine learning). Il modello di un sistema appreso empiricamente può essere usato per controllare il sistema stesso. Quando le due fasi di identificazione e di controllo sono contestuali, ossia quando si tenta al contempo di usare la conoscenza di un modello e la retroazione per fornire ingressi di controllo al sistema, e di usare la misura delle uscite corrispondenti a tali ingressi per migliorare la conoscenza del modello stesso e adattarsi alle sue variazioni, si parla di controllo adattativo. Lo studio del controllo adattativo, iniziato sin dagli anni Sessanta del 20° sec., ha dato luogo ad alcuni importanti sviluppi e applicazioni, per es., nel campo della robotica. La difficoltà del problema, tuttavia, è tale che esso si può considerare ancora uno dei campi di ricerca più aperti e impegnativi.
Un terreno di grande potenziale sviluppo e di difficili sfide intellettuali per la t. del c. è quello dei sistemi costituiti da molti agenti parzialmente o totalmente autonomi, che possono interagire tra loro in collaborazione, in competizione o con scopi indipendenti. Sistemi di questo genere si incontrano, per es., nello studio di problemi economico-finanziari, ecologici o sociologici, ma se ne prevede l'utilizzo anche nelle nuove generazioni di sistemi per l'assistenza alla guida e alla gestione del traffico (aereo, navale o persino di auto private, come, per es., nella guida assistita in caso di nebbia), o in sistemi multirobot per l'esplorazione o la sorveglianza. In questi sistemi, che si prevede saranno molto diffusi anche in seguito alla diffusione delle tecnologie di comunicazione senza fili, le azioni da intraprendere devono essere decise da ogni agente in modo decentralizzato, ossia senza la possibilità di conoscere l'intero stato del sistema, ma solo sulla base di conoscenze limitate a una zona individualmente accessibile e con informazioni scambiate tra agenti vicini. Una delle più stimolanti sfide aperte alla t. del c. è certamente come fare in modo che dal sistema complesso originato dalla interazione di molteplici volontà distinte emerga un comportamento complessivo coerente e sicuro. Per la sua capacità di studiare sistemi complessi astraendo dai dettagli e fornendo linguaggi e strumenti comuni a domini diversi, è opinione diffusa che la t. del c. rivesta un ruolo cruciale e crescente nello sviluppo economico e industriale delle società avanzate. La t. del c. è situata, infatti, al crocevia dove le scienze dell'informazione s'incontrano con le principali tecnologie moderne: con quelle industriali, in tutte le applicazioni in cui si cerca di costruire macchine con sempre maggiore intelligenza, legando per così dire l'acciaio e il silicio; e con quelle biologiche e medicali, attraverso le quali si vogliono governare intelligentemente complessi processi fisiologici, biologici o ambientali mediante un'efficace ma sicura integrazione tra il naturale e l'artificiale.