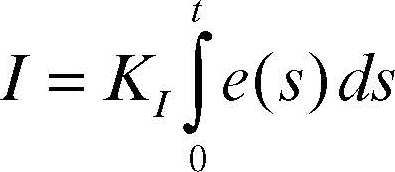controllo, teoria del

controllo, teoria del

controllo, teoria del disciplina che si occupa di analizzare le variazioni temporali nella risposta di un determinato sistema dinamico, al variare delle sollecitazioni ricevute dal sistema stesso. In particolare, vengono studiati opportuni sistemi di controllo, in grado di alterare le sollecitazioni ricevute da un sistema (gli ingressi) in modo da ottenere una risposta (uscita) desiderata. Un esempio di sistema di controllo è un termostato che modifica il riscaldamento o il raffreddamento di un sistema per mantenerlo a una temperatura prefissata. Due i tipi principali di sistemi di controllo. Nel sistema a catena aperta (detto anche predittivo o feed-forward) il valore dell’ingresso viene alterato in base alle proprietà del sistema senza conoscere il valore dell’uscita. Nel sistema a retroazione (detto anche a controreazione o a feed-back) il valore dell’uscita interagisce con l’ingresso in modo da mantenere l’uscita al valore desiderato. Per esempio, un condizionatore d’aria regola la temperatura dell’aria fredda emessa (ingresso) proporzionalmente alla differenza tra la temperatura impostata (uscita desiderata) e la temperatura effettivamente misurata (uscita effettiva).

Particolarmente sviluppata è la teoria del controllo per i sistemi lineari. Se la relazione che lega l’uscita y all’ingresso x è data da y = ƒ(x), il sistema si dice lineare se per ogni ingresso del tipo ax₁ + bx₂, con a e b costanti, l’uscita vale: y = ƒ (ax₁ + bx₂) = ƒ(ax₁) + ƒ(bx₂) = ay₁ + by₂, dove y_i è l’uscita corrispondente all’ingresso x_i. Questa proprietà implica che l’uscita corrispondente a una combinazione lineare di ingressi è la combinazione lineare delle uscite corrispondenti ai singoli ingressi. Poiché dal punto di vista matematico è molto più agevole la trattazione dei sistemi lineari, tipicamente si adottano opportune tecniche di linearizzazione, valide per piccole variazioni o in un intorno di un punto particolare, per trattare il controllo di sistemi non lineari.

Un sistema di controllo particolarmente diffuso nei sistemi a retroazione è il controllo pid (controllo Proporzionale-Integrale-Derivativo). Un tale sistema di controllo è costituito da tre stadi. Lo stadio proporzionale aggiusta l’ingresso proporzionalmente all’errore, cioè proporzionalmente alla differenza tra l’uscita desiderata e l’uscita effettiva: P = K_p e(t) dove e(t) è il valore istantaneo dell’errore e K_p è il coefficiente di guadagno dello stadio proporzionale. Il guadagno proporzionale, opportunamente regolato, rende stabile il sistema; guadagni proporzionali elevati, inoltre, fanno sì che sia più veloce la riduzione dell’errore a zero, anche se, oltre un certo limite, in genere il sistema tende a diventare instabile. Lo stadio integrale modifica l’ingresso in base all’evoluzione temporale nel passato dell’errore:

La presenza di tale stadio velocizza il raggiungimento dell’uscita desiderata, ma può portare a una correzione eccessiva, che deve essere compensata da una correzione nel verso opposto.

Infine, lo stadio derivativo aggiusta l’ingresso in base alla velocità di variazione dell’errore:

La presenza di questo stadio riduce la possibilità di una correzione eccessiva, ma può rallentare il raggiungimento del livello desiderato per l’uscita. I coefficienti di guadagno possono essere alterati separatamente per modificare il contributo di ciascuno stadio e migliorare l’efficienza del processo di controllo (→ trasferimento, funzione di; → operatori collegati in retroazione).