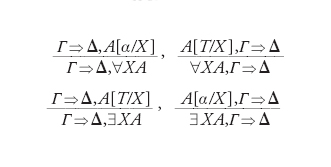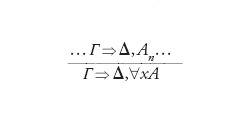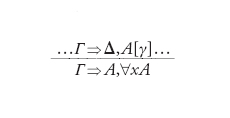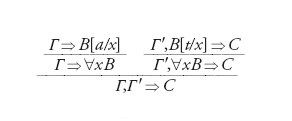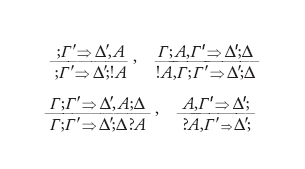Dimostrazione, teoria della
Dimostrazione, teoria della
La teoria della dimostrazione nasce negli anni Venti del Novecento come strumento di realizzazione del programma di David Hilbert per la fondazione della matematica. In quanto tale, ha avuto sin dall'inizio un carattere riduzionista che è andato man mano affievolendosi nel tempo; da una parte in vista di risultati negativi come il teorema di indecidibilità di Kurt Gödel, che sembravano vanificare il programma nelle sue forme più estreme, dall'altra per i sempre più frequenti contatti con discipline vicine come l'informatica teorica, che ne hanno allargato gli orizzonti.
Alla base del programma di Hilbert sta l'idea che ‒ ai fini dell'analisi della correttezza e affidabilità ‒ le teorie matematiche si possono vedere come sistemi deduttivi definiti in opportuni linguaggi formali aventi un carattere puramente combinatorio, specificabile in termini di insiemi di assiomi e di regole di deduzione algoritmicamente dominabili. L'idea è che, a prescindere da ogni riferimento agli oggetti astratti di cui le teorie intendono parlare, dal punto di vista operativo esse sono dispositivi per generare teoremi e sono accettabili nella misura in cui non generano contraddizioni. Giustificare formalmente una teoria significa allora provare, utilizzando strumenti che riguardino esclusivamente l'aspetto combinatorio della teoria e quindi non presuppongano nulla di astratto, che questo non si verifica. Di qui l'interesse per lo studio delle dimostrazioni e la limitazione a metodi finitari. Come mostra però il teorema di Gödel, per sistemi forti almeno come certi frammenti dell'aritmetica è possibile tradurre lo studio di formule e dimostrazioni in studio su numeri e loro proprietà; in questa traduzione la coerenza dell'aritmetica ‒ nessuna dimostrazione d può terminare con 0≠1 ‒ diviene un enunciato universale ∀n A(n) che coinvolge l'infinito e il tentativo di provarla finitisticamente si rivela per quello che è: un tentativo di eliminare l'infinito.
Almeno a partire dagli anni Cinquanta ‒ soprattutto per opera di studiosi come Georg Kreisel ‒ gli orizzonti della teoria della dimostrazione sono cambiati e ha avuto inizio un lavoro sistematico volto a chiarire in generale la natura e i limiti dei programmi riduzionisti e anche gli scopi dell'analisi delle dimostrazioni. Questo lavoro ha portato a diversi tipi di progetti e risultati.
Da una parte, l'allargarsi dell'interesse per le diverse forme di pensiero costruttivista e l'individuazione di precise teorie formali in grado di codificare la pratica finitista, intuizionista o predicativista nel campo dell'aritmetica, dell'analisi, dell'algebra e di altri settori centrali della matematica. Dall'altra, parallelamente alle ricerche sui sistemi in grado di codificare le varie forme di matematica costruttiva, si situa lo studio delle loro proprietà metamatematiche, che ha portato all'introduzione di nuove tecniche nello studio della teoria della dimostrazione.
Esempi particolarmente significativi sono il complesso di lavori legati al concetto di realizzabilità iniziati da Stephen C. Kleene per dare una semantica costruttiva alla logica intuizionista e lo sviluppo sistematico del collegamento tra derivazioni naturali e funzionali (il cosiddetto isomorfismo di Curry-Howard) con i conseguenti rapporti con il lambda calcolo che coinvolgeranno più tardi anche la teoria delle categorie. Dal punto di vista della teoria riduzionista i risultati più significativi sono quelli legati alla congettura di Takeuti e all'Hauptsatz per teorie in linguaggi più forti di quelli elementari, soprattutto il secondo ordine e i linguaggi infinitari (omega-logica, teoria delle definizioni induttive ecc.).
Connessa a queste indagini sin dai primi lavori di Gerhard Gentzen è l'analisi delle dimostrazioni in logiche più deboli di quella classica, prima fra tutte quella intuizionista e il suo frammento minimale. Anche per questi sistemi è possibile una dimostrazione dell'Hauptsatz e dal principio della sottoformula che ne consegue si ottengono come corollari non solo risultati importanti quali il teorema d'interpolazione di Craig e Lyndon, validi anche per la logica classica, ma pure teoremi specifici della logica intuizionista come la proprietà dell'esistenziale o quella della disgiunzione. Uno dei portati più significativi di queste indagini è stato il tentativo sistematico di individuare, sulla base della teoria della dimostrazione, i principî che stanno a fondamento di queste diverse logiche e spiegano la loro unità. In questa direzione si situano le ricerche sulla logica lineare come logica di base che Jean-Yves Girard ha iniziato dai primi anni Ottanta e che hanno realizzato profondi e inediti contatti con l'informatica teorica e la teoria delle categorie.
Il calcolo classico dei sequenti
Lo strumento centrale di cui ci serviremo sono i calcoli di sequenti, o L-calcoli, introdotti da Gentzen nel 1935. Essi sono formulati in linguaggi privi di identità e con ⊥, il simbolo che indica l'assurdo. I sequenti sono espressioni della forma A1,...,An ⇒B1,…,Bk, che vanno lette come il condizionale A1⋀ … ⋀An⇒ 1⋁ ... ⋁Bk; nel caso n=0 scriveremo ⇒B1,…,Bk e nel caso k=0 la formula equivarrà a (A1⋀… An)⇒⊥. Vedremo più avanti come il calcolo si possa estendere a linguaggi più forti; limitiamoci per ora al caso del primo ordine classico ‒ privato dell'identità ‒ introducendo il sistema LK.
Il sistema LK è costituito da tre gruppi di regole di inferenza: Identità, Struttura e Logica, dove Γ, Δ, Λ, ecc. indicano insiemi finiti di formule, eventualmente anche vuoti.
Alcune osservazioni. La regola del taglio è la più importante del sistema e rappresenta una sorta di transitività della nozione di deduzione. La sua presenza o assenza è la posta in gioco in gran parte dei teoremi della teoria della dimostrazione. Il gruppo strutturale si occupa della gestione delle successioni di formule e, dopo il taglio, le regole di contrazione sono le più importanti del sistema. Nella regola di scambio σ indica una qualsiasi permutazione. Il gruppo logico si occupa infine della introduzione di formule con nuovi simboli ‒ connettivi o quantificatori ‒ a destra o a sinistra di ⇒. Per quanto riguarda i quantificatori, con A[t/x] indichiamo la sostituzione, che scriveremo anche At. Sorvolando su alcune pur necessarie precisazioni, ricordiamo solo che le regole ⇒∀ e ∃⇒ sono soggette alla restrizione che il parametro a non deve occorrere nella conclusione.
Concatenando le regole si ottiene la nozione di dimostrazione ed è immediato provare che LK risulterà valido rispetto alla semantica classica, nel senso che se A è una formula chiusa e il sequente ⇒A è dimostrabile in LK allora A è una legge logica. Quanto alla completezza, essa si può formulare dicendo che ⇒A è dimostrabile in LK oppure ⌝A ha un modello. Il risultato si può ottenere cercando di scrivere una dimostrazione di ⇒A nel calcolo; si parte da ⇒A e si prende una regola di cui sia conclusione. Consideriamo quindi le premesse (nessuna, una o due) e per ciascuna cerchiamo le regole di cui possono essere conclusioni. Iterando il procedimento, si finirà con l'ottenere un albero le cui ramificazioni sono tutte corrette: se è finito sarà una dimostrazione di ⇒A, altrimenti ci sarà almeno un ramo infinito ai cui vertici stanno sequenti Γn ⇒Δn che possiamo completare in modo da ottenere un modello: basterà prendere come dominio i termini ottenuti dai parametri introdotti dalle regole ⇒∀ e ∃⇒ dando valore 1 alle formule nei vari Γn e valore 0 a quelle nei Δn. La struttura così ottenuta sarà modello di Γ0 e contromodello di Δ0, così che ⌝A sarà vero.
Hauptsatz e risultati connessi
Il risultato più importante su LK dal punto della teoria della dimostrazione è il cosiddetto Hauptsatz (teorema fondamentale) di Gentzen, dimostrato nel 1935: esso ci dice che se ⇒A è dimostrabile in LK, lo sarà anche senza utilizzare la regola del taglio. Il teorema si dimostra eliminando progressivamente le applicazioni della regola: tagli su formule complesse vengono rimpiazzati da tagli su formule più semplici e l'algoritmo per far questo richiede una definizione induttiva complicata. è possibile d'altra parte un'interpretazione semantica dell'Hauptsatz: se nella dimostrazione di completezza non si fa ricorso alla regola del taglio, un eventuale ramo infinito dà origine a un'interpretazione a tre valori se poniamo tra i possibili valori delle formule un valore 1/2, indeterminato, e valutiamo quelle composte in modo che per 0 e 1 il loro valore determini, come nella definizione bivalente, quello delle componenti. Come mostrato da Kurt Schütte nel 1960, si può allora provare che una formula chiusa A è dimostrabile senza tagli in LK se e solo se in ogni interpretazione a tre valori non assume mai il valore 0. Si verifica infatti che la regola del taglio non vale in queste interpretazioni: da ⇒A (A non è 0) e A⇒B (se A è 1, allora B non è 0) non si può ottenere ⇒B (B non è 0). Da qui segue con facilità una dimostrazione semantica dell'Hauptsatz. Nello stesso ordine di idee, Schütte ha anche mostrato come si può distinguere a livello dimostrativo tra occorrenze positive e negative di costanti relazionali entro le formule. Un'applicazione è il teorema di Roger C. Lyndon (1959) sull'esistenza di formule interpolanti, che si può dimostrare dall'Hauptsatz come del resto fatto originariamente da Lyndon stesso.
Altra conseguenza importante è il théorème fondamental, dimostrato da Jacques Herbrand nel 1930. Supponiamo che A sia una formula prenessa, per esempio
[1] ∃x, ∀y, ∃z, ∀w R(x,y,z,w).
La trasformata di Herbrand AH si ottiene cancellando i quantificatori universali e sostituendo a ogni variabile quantificata universalmente una nuova costante funzionale che ha come argomenti le variabili esistenzialmente quantificate che la precedono nel prefisso; nel nostro esempio AHsarà
[2] ∃x, ∃z R(x,f(x),z,g(x,z)).
Il teorema di Herbrand ci dice che A è dimostrabile in LK se e solo se esistono un n≥1 e degli esempi A1,….,An della matrice di AH per cui A1 … Anè tautologia. Il teorema di Herbrand è la controparte sintattica del teorema di Skolem e, fatto importante, ammette una dimostrazione puramente sintattica. Si può infatti ottenere una versione in termini di sequenti del teorema di Herbrand come raffinamento dell'Hauptsatz, mediante il teorema del sequente mediano di Gentzen. Esso afferma che se una formula prenessa A è dimostrabile classicamente allora avrà una dimostrazione senza tagli strutturata attorno a un sequente mediano Γ⇒Δ, dove Γ non contiene quantificatori e sotto Γ⇒Δ ci sono solo applicazioni di ⇒∀, ∃⇒ e contrazioni, che sono regole unarie. In altre parole, sino al sequente mediano si usano solo regole sui connettivi, dal sequente mediano in poi si applicheranno solo contrazioni e regole che introducono quantificatori. Il sequente mediano, quindi, contiene solo esempi e in particolare ‒ poiché le formule del conseguente vanno lette come una disgiunzione ‒ sarà una disgiunzione di esempi di una matrice; nel caso della A di sopra, la disgiunzione avrà la forma R(s1,t1,u1,v1) … R(sn,tn,un,vn). Per chiarezza possiamo isolare il nucleo centrale del teorema di Herbrand nel principio seguente sulle formule esistenziali: ⇒∃xA è dimostrabile in LK se e solo se si possono trovare termini t1,…,tnper cui
[3] A(t1) … A(tn)
è dimostrabile in LK. Questo è un esempio di quel processo di esplicitazione su cui torneremo parlando del sistema intuizionista LJ.
Il corollario più importante dell'Hauptsatz dal punto di vista del programma hilbertiano è però il principio della sottoformula, in base al quale nella ricerca di una dimostrazione per ⇒A ci si può limitare a sequenti costituiti da sottoformule di A. Questo è chiaramente possibile per l'eliminazione dei tagli; in tutte le altre regole infatti le premesse sono costituite da sottoformule di formule della conclusione. è in questo senso che il teorema ci dà una sorta di eliminazione dell'infinito. Se infatti A è priva di quantificatori e si deve dimostrare ⇒A, non occorrerà ricorrere al dominio illimitato dei termini ma solo a quelli ‒ finiti ‒ coinvolti direttamente dalla formula. Da qui è facile provare la coerenza di LK e ottenere un metodo di decisione per il frammento enunciativo. Il limite è che esso si applica esclusivamente al calcolo e non a teorie come l'aritmetica o la teoria degli insiemi, per le quali ci darebbe una prova della non dimostrabilità di 0≠1 e quindi della loro coerenza.
Calcoli di sequenti e programmazione logica
La proprietà della sottoformula, presente in tutti i calcoli di sequenti per cui vale una forma di Hauptsatz, enuncia una specie di localizzazione della nozione di dimostrazione ed è possibile sfruttare questa localizzazione ai fini della dimostrazione automatica. Come si è detto, per dimostrare ⇒A è sufficiente considerare sequenti che contengono solo sottoformule di A. Se però le sottoformule di una formula priva di quantificatori sono in numero finito, questo non vale per le formule in cui occorrono variabili quantificate; in particolare, le sottoformule di ∀xA(x) sono tutti gli esempi A(t) e costituiscono una totalità potenzialmente infinita. Il principio della sottoformula quindi non ci dà tanto una riduzione al finito quanto un'approssimazione a esso, che però non raggiungiamo mai. L'idea della ricerca automatica di prove a partire dal calcolo dei seguenti è alla base del metodo della risoluzione di J. Alan Robinson (1986). Si tratta di trovare le conseguenze ‒ di fatto solo quelle di una certa forma ‒ di un dato insieme Γ di assiomi. Manipolazioni standard ci permettono di riformulare l'insieme di assiomi come insieme di clausole, cioè sequenti p1,…,pn⇒ q1,….,qm dove le pie qjsono atomiche (diverse dal falso ⊥). Di fatto, la tecnica è veramente efficace solo nel caso delle clausole di Horn, vale a dire clausole della forma p1,…,pn⇒q, e per dei goal del tipo ∃y1,…,∃up A, dove A è una congiunzione D1 … Dtdi formule atomiche. Se indichiamo con Γ′ l'insieme di tutte le clausole ottenute per sostituzione da quelle in Γ, possiamo allora concludere in base all'Hauptsatz che:
a) Una formula B=∃y1,…,∃yp A, dove A è una congiunzione D1 … Dt di atomiche, è conseguenza di Γ se e solo se si possono trovare termini t1,…,tptali che tutte le Dj[t1,…,tp] siano conseguenze di Γ′.
b) Una formula atomica D è conseguenza di Γ se e solo se la si può dimostrare da Γ utilizzando solo la regola del taglio.
Possiamo quindi restringere l'uso della regola del taglio alle formule atomiche.
Il teorema precedente è alla base della programmazione logica e il problema che si pone è trovare tutte le sostituzioni tali che D1 … Dt sia conseguenza di Γ′. A questo scopo si utilizza la teoria dell'unificazione, che ci permette di restringere la ricerca dei termini da sostituire: quando è possibile unificare p e q ‒ vale a dire sostituire dei termini in p e q in modo da ottenere la stessa formula ‒ esiste un unificatore principale (il più generale) al quale ci si può restringere. Ciò nonostante, la ricerca automatica resta impraticabile in un buon numero di casi e per questo motivo in linguaggi come PROLOG si permettono deviazioni rispetto al teorema. Malgrado queste difficoltà, si tratta sicuramente di una linea di ricerca promettente che mostra come i primi studiosi di teoria della dimostrazione avessero avuto ragione a ostinarsi nella strada, apparentemente senza sbocco, di Hilbert.
La congettura di Takeuti
Il calcolo LK come detto sopra si può estendere a linguaggi più forti di quelli del primo ordine e in particolare a quelli del frammento monadico del secondo ordine, dove si considerano solo variabili X,Y,Z,… su insiemi. In questo caso si introducono i termini d'insieme {x∣B} dove B è una formula qualsiasi da noi interpretata come l'insieme degli oggetti che godono di B. La sostituzione di un termine T={x∣B} a X in A, che indicheremo con A[T/X], consiste nel rimpiazzare ogni occorrenza di X con T per poi rimpiazzare le formule atomiche T(t) con B[t/x].
Il calcolo G1LG che considereremo è esattamente come LK, ma con in più le seguenti regole specifiche per il secondo ordine:
Queste obbediscono alle convenzioni per cui in ⇒∀2 e ∃2⇒ il parametro del secondo ordine α non compare nella conclusione e in ⇒∃2 e ∀2⇒; T è invece un termine qualsiasi.
Le regole ⇒∃2 e ∀2⇒ permettono di dimostrare lo schema di comprensione ∃X ∀x (X(x)→A[x]): basterà partire da ∀x(A→A) e applicare ⇒∃2 utilizzando il termine {x∣A}.
Lo schema di comprensione, introdotto a suo tempo da Gottlob Frege, ci permette di definire un insieme a partire da una proprietà ed è un principio estremamente forte. La congettura di Takeuti ‒ formulata nel 1953 ‒ postulava l'eliminazione della regola del taglio ed è stata dimostrata in due tappe. In un primo tempo, nel 1960, Schütte ne ha dato una formulazione semantica in termini di modelli a tre valori, che poi William Tait ha dimostrato nel 1965. Solo in un secondo tempo si è affrontata la versione sintattica, formulata per la versione intuizionista del sistema e provata da Girard nel 1970. La congettura implica la coerenza dell'aritmetica al secondo ordine, in cui è possibile sviluppare l'analisi classica e gran parte della matematica tradizionale. Sfortunatamente, però, i principi utilizzati a livello metateorico sono così forti da rendere inutilizzabile il risultato dal punto di vista riduzionista hilbertiano. Il fatto più grave è che la maggior parte dei corollari interessanti dell'Hauptsatz cessano di essere validi, primo fra tutti il principio della sottoformula. Le regole ⇒∀2 e ∃2⇒ infatti considerano come sottoformule di ∀X A e ∃X A le formule A[T/X] e le loro sottoformule; non appena X apparirà in A sarà quindi possibile ottenere qualunque formula B come sottoformula di ∀X A o ∃X A. Ne segue che il principio della sottoformula deve essere ristretto e vale solo per i sequenti che non contengono quantificazioni del secondo ordine.
La teoria infinitaria della dimostrazione
Nel 1936 Gentzen dette una dimostrazione della coerenza dell'aritmetica che ha aperto un campo di ricerca molto controverso, la teoria infinitaria della dimostrazione. In essa si utilizzano sul piano metateorico o nella stessa formalizzazione metodi e concetti di carattere infinitario. Se non ci sono dubbi sulla qualità scientifica di alcuni di questi lavori, le perplessità riguardano da una parte il loro significato epistemologico e dall'altra il carattere settoriale delle tecniche usate, che non ha trovato applicazioni in discipline collegate come per esempio l'informatica. Ciò non toglie che i contributi in quest'ambito abbiano storicamente una posizione centrale nello sviluppo della teoria della dimostrazione. Ci limiteremo quindi a una descrizione per sommi capi.
L'aritmetica e l'ordinale ε0
Il lavoro di Gentzen cui abbiamo fatto riferimento è posteriore ai contributi di Gödel e prende atto dell'impossibilità di dare una dimostrazione finitista della coerenza dell'aritmetica utilizzando procedure induttive limitate a predicati ricorsivi. L'idea di Gentzen è di dimostrare l'Hauptsatz per una formalizzazione AP dell'aritmetica nel calcolo dei seguenti e il modo per farlo è definire induttivamente un algoritmo che elimini le applicazioni della regola del taglio. Già nel caso di LK si vede che questo può provocare un'enorme crescita della complessità delle dimostrazioni, ma la cosa diventa ancora più drammatica nel caso di AP perché il rapporto tra la complessità della dimostrazione di partenza e quella senza tagli che si ottiene non è maggiorato nemmeno da una funzione ricorsiva primitiva. Per dimostrare la convergenza dell'algoritmo di eliminazione dei tagli occorre quindi ricorrere a un'induzione su ε0, un ordinale molto più alto di ω e il primo α per cui α=ωα. Dimostriamo così la coerenza del principio d'induzione su ω ricorrendo a un ordinale ben più grande di ω! Una sorta di conferma, d'altra parte, che esso in qualche modo misura una complessità intrinseca del problema della coerenza dell'aritmetica ci viene dal fatto che, quando nel 1958 Gödel estenderà il punto di vista finitista con lo scopo esplicito della dimostrazione della coerenza di AP mediante l'introduzione di funzionali ricorsivi di tipo finito, per provare la correttezza della teoria di questi funzionali ritroverà l'ordinale ε0. Sarebbe sbagliato però concludere che risultati come questi non dicano nulla; sicuramente non attuano una riduzione dell'infinito al finito ma ci permettono di comprendere meglio la dinamica del finito.
La ω-logica e sue generalizzazioni
Dopo i lavori di Gentzen del 1936, l'utilizzazione degli ordinali transfiniti diviene uno dei temi di ricerca preferiti della teoria della dimostrazione, soprattutto di scuola tedesca. è innegabilmente Schütte il protagonista di questo indirizzo d'indagine, che si caratterizza per l'uso di sistemi infinitari di dimostrazione che contengono la cosiddetta ω-regola. Nel caso di ⇒∀, essa si presenta nella forma
dove il numero delle premesse è infinito: per dimostrare ∀xA si dimostrano tutti i casi di An. è chiaro che in questo modo riassorbiamo il principio di induzione ed estendendo al sistema l'Hauptsatz possiamo ottenere il principio della sottoformula e di qui la coerenza dell'aritmetica. Il ricorso a dimostrazioni infinite si può giustificare osservando che esse si possono vedere all'interno di una concezione potenziale dell'infinito stesso, anche se comunque non esiste alcun modo di controllarle rimanendo nel finito. Il vantaggio di questa estensione infinitaria sta nel fatto che le ω-dimostrazioni godono di proprietà notevoli. In primo luogo, come è stato detto, hanno come conseguenza il principio d'induzione; in secondo luogo, per loro possiamo ottenere un risultato di completezza del sistema rispetto agli ω-modelli, quei modelli cioè che hanno come dominio l'insieme ℕ dei naturali. Infine, l'Hauptsatz mantiene tutti i suoi corollari (tranne il teorema d'interpolazione, a meno che si accettino interpolanti infiniti) e anche in questo caso per dimostrarlo è necessaria l'induzione sino a ε0. Un possibile modo di interpretare il risultato può essere concepirlo in termini di uno scambio tra quantificatori numerici e esponenziale ordinale. Il ragionamento per induzione nella dimostrazione dell'Hauptsatz dipende infatti da due parametri: la complessità della formula su cui si ragiona e la lunghezza dell'induzione. Se si vuole eliminare un quantificatore nella formula lo si può fare solo incrementando la lunghezza e all'inverso se si vuole ridurre la lunghezza sarà necessario complicare la formula medesima. Ci muoviamo quindi tra due estremi: l'induzione semplice su ω relativa a tutte le formule (quella codificata in AP) e l'induzione su ε0 (usata a livello metateorico) che possiamo restringere a formule prive di quantificatori.
Tecniche analoghe si possono applicare anche alla teoria ID1 delle definizioni induttive utilizzando la α-regola, dove α è un ordinale:
Una β-dimostrazione consiste nel dare, per ogni ordinale α, una dimostrazione Π(α) che utilizza la α-regola qui sopra con tante premesse quanti gli ordinali γ〈α. Queste dimostrazioni devono essere tra loro collegate da un principio d'uniformità, così che se f: α→α′ è una funzione strettamente crescente si può definire una α-dimostrazione ‒ l'immagine reciproca di Π(α′) che indicheremo con f−1(Π(α′)) ‒ e si richiede che f−1(Π(α′))=Π(α). Questo ha delle conseguenze sorprendenti, per esempio che la famiglia delle Π(n) per n naturale determina tutte le Π(α) quale che sia α. Così una β-dimostrazione sarà una famiglia di dimostrazioni finite ma d'altra parte sarà corretta solo se la sua dilatazione in una grandezza ordinale α arbitraria non ha rami infiniti. La β-logica ha proprietà analoghe alla ω-logica: una proprietà di completezza, risultati sull'eliminazione del taglio, corollari analoghi al principio della sottoformula e ‒ ammesse formule infinite ‒ anche un teorema di interpolazione.
Un approccio analogo si può sviluppare anche per sistemi più forti dell'aritmetica: oltre alla teoria ID1 delle definizioni induttive, i vari sistemi di analisi predicativa studiati da Solomon Feferman, Wolfram Pohlers e Wilfried Sieg (1981), i sottosistemi impredicativi dell'analisi indagati da Wilfried Bucholtz e Schütte (1988) etc. Per ciascuna di queste teorie si può dimostrare una forma di Hauptsatz mantenendo tutti o parte dei corollari che abbiamo visto sopra.
Il calcolo dei sequenti per la logica intuizionista
Sin dal 1935 Gentzen aveva affiancato a LK un calcolo LJ per la logica intuizionista ottenibile da LK con due sole modifiche: 1) non prendendo ⌝ come connettivo primitivo ma definendo A come (A⇒); 2) limitandosi a sequenti del tipo Γ⇒A. Alternativamente, si può lasciare come primitivo ⌝, ma in questo caso vanno esclusi i sequenti con più di una formula nel conseguente. Una delle ragioni dell'interesse per il modo di presentare la logica in termini di sequenti è stato fin da subito il fatto che essi permettono di vedere in modo unitario i rapporti tra logica classica e intuizionista. Anche in quest'ultimo caso il risultato fondamentale rimane l'Hauptsatz e possiamo provare che esiste una procedura effettiva per eliminare i tagli dalle dimostrazioni di LJ. L'argomento è particolarmente complesso e si articola in due tipi di passi fondamentali. Il primo consiste nella sostituzione di un taglio su A con tagli su A con premesse che risultino conclusioni di regole logiche che a loro volta introducono A sia a destra che a sinistra. Per esempio, se A è ∀xB abbiamo la dimostrazione
Si tratta di una trasformazione costosa dal punto di vista algoritmico, che ci può far passare da una dimostrazione di complessità n a una di complessità 2n. L'altro tipo di passo consiste nel sostituire tagli ottenuti come sopra con tagli su sottoformule. In questo caso non si aumenta la complessità e il numero di regole della dimostrazione diminuisce. Iterando le due operazioni si diminuisce il grado dei tagli, vale a dire il massimo numero di costanti logiche in una formula più uno. Il grado 0 è quello delle dimostrazioni senza tagli e i due tipi di passi sopra descritti abbassano il grado di un'unità. La complessità della dimostrazione ottenuta può così risultare una torre di esponenziali.
Corollari saranno il principio della sottoformula (che ci dà un metodo di decisione per il frammento enunciativo) e i seguenti nuovi principî, privi di controparte nel caso classico.
1) Proprietà della disgiunzione: se ⇒A B è dimostrabile in LJ, saranno dimostrabili ⇒A oppure ⇒B.
2) Proprietà dell'esistenziale: se in LJ si dimostra ⇒∃xA, allora si dimostra anche ⇒A[t/x] per un termine t.
Principi del genere non valgono in LK perché possiamo sempre ipotizzare che l'ultima regola sia una contrazione. Ciò che la restrizione a sequenti ⇒A fa è appunto impedire la contrazione a destra. Questi due risultati ci offrono un'altra interpretazione del significato dell'Hauptsatz non più come strumento per l'eliminazione dell'infinito quanto come modo per eliminare l'implicito. è facile vedere, infatti, che entrambi ci permettono di affermare che la dimostrabilità di un enunciato contenente informazioni implicite (il t per cui A(t/x) o il disgiunto da cui si ottiene A B) rimanda alla dimostrabilità di un enunciato che rende esplicito quanto in esso è implicito.
Nella pratica matematica non si dimostra mai un risultato per verifica diretta (prova esplicita), ma piuttosto tramite un détour concettuale (prova implicita). La possibilità di manipolare l'implicito è completamente localizzata nella regola del taglio, che permette di concludere B a partire da un lemma A e da una dimostrazione di B sotto l'ipotesi A (cioè ⇒B a partire da ⇒A e A⇒B). Non si può ragionare senza usare dei tagli e il significato dell'Hauptsatz, che sembra affermare il contrario, è che dimostrazioni che non li usano sono possibili ma artificiali. Questa artificialità può essere utile se vogliamo passare dall'esistenza di individui che soddisfano date proprietà al calcolo concreto. Un calcolo però imperniato sull'algoritmo per l'eliminazione dei tagli che ci ha portato alle proprietà dell'esistenziale e della disgiunzione sarebbe certamente noioso e non potremmo affidarlo a una macchina. è per questo che il tema dell'esplicitazione radica la teoria della dimostrazione nell'informatica. La nuova teoria della dimostrazione, nata negli anni Ottanta, non è più interessata a eliminare l'infinito per giustificarlo ‒ come era nelle intenzioni di Hilbert ‒ ma vuole piuttosto studiare la dinamica di questa eliminazione, la sua natura di esplicitazione e le sue affinità profonde con l'informatica.
La logica lineare
Il cambiamento di ottica indotto dall'informatica ha portato a un nuovo interesse per la teoria della dimostrazione enunciativa in collegamento con il λ-calcolo dei tipi. I tipi ‒ come posto in evidenza dai lavori di Haskell B. Curry e poi di William Howard (1969) ‒ non sono che una variante notazionale di quegli N-calcoli introdotti da Gentzen di cui LJ dà una versione in termini di sequenti. Questi collegamenti mettono in luce che le complicazioni della dinamica dello Hauptsatz sono essenzialmente dovute alla regole di contrazione.
Questo ci dà l'occasione di verificare più da vicino le ragioni per assumere le diverse regole strutturali. La regola di scambio equivale a un assioma del tipo A B →B A e quindi a una sorta di commutatività certo discutibile (si pensi a una lettura di → come 'e poi'), ma ricordando che nel complesso le prospettive di una logica non commutativa sembrano confuse. La regola di indebolimento può essere invece assimilata a un principio del tipo A→(B→A), che è stato più volte messo in dubbio (si pensi a una lettura causale di → o ad una in termini di rilevanza): come tale potrebbe quindi essere revocata. Ma è la contrazione che, se letta come A →A A, ci dà il principio più dubbio. In base a essa da A e A→B non solo concluderemmo B ma potremmo conservare A per utilizzazioni ulteriori. In questo senso la regola ci coinvolge nel processo infinito che nasce da questa possibilità di iterazione. Più concretamente, è la contrazione a essere responsabile dell'indecidibilità della logica del primo ordine stabilita dal teorema di Church. Senza contrazione sarebbe infatti possibile limitare il numero delle formule nei sequenti e quindi la proprietà della sottoformula ci permetterebbe di estendere anche al primo ordine la decidibilità che abbiamo nel caso enunciativo. Stesso discorso per le disgiunzioni di Herbrand, che sarebbero tutte di lunghezza unitaria fornendoci un altro algoritmo di decisione. Per queste ragioni, la logica lineare ‒ introdotta da Girard nel 1986 ‒ rifiuta indebolimento e contrazione come regole strutturali. Dal momento però che il calcolo così ottenuto sarebbe troppo poco espressivo senza queste regole, le reintroduce sotto forma diversa per mezzo di due nuovi connettivi, ! e ?. Quando le formule utilizzano un numero sufficiente di ! e ? si ritrova il comportamento abituale, classico o intuizionista, così che nulla viene perduto. In questo senso la logica lineare è uno strumento che ci permette di studiare altri sistemi. Ma come gestire questa pluralità di logiche?
Il sistema LU
L'idea alla base del sistema LU introdotto da Girard nel 1991 è che ‒ per realizzare in concreto l'unità tra le diverse logiche classica, intuizionista e lineare ‒ è necessario distinguere all'interno dei sequenti due zone che avranno comportamento diverso rispetto alle regole strutturali. Scritto un sequente nella forma Γ;Γ′⇒Δ′;Δ, la zona centrale formata da Γ′ e Δ′ sarà a gestione classica mentre la zona periferica formata da Γ e Δ sarà a gestione lineare. In questo modo tutte le regole strutturali si potranno applicare su Γ′ e Δ′ mentre solo lo scambio varrà per Γ e Δ. C'è però comunicazione tra zona classica e lineare, così che sarà possibile passare dall'una all'altra a seconda della polarità delle formule. Le formule a polarità positiva +1 possono passare da Γ′ a Γ mentre le formule a polarità negativa −1 possono passare da Δ′ a Δ. Ogni formula avrà un'unica polarità: positiva, negativa o neutra, cioè 0. L'applicazione dei connettivi e dei quantificatori darà alle formule risultanti una polarità in funzione di quella delle sottoformule. La tabella ci illustra la situazione per i connettivi non lineari.
Il connettivo ⊃ e il quantificatore Λ sono intuizionisti, i connettivi ⌝, → e il quantificatore ∀ sono classici, gli altri comuni. Per quanto riguarda i connettivi lineari, il discorso è più semplice e !A avrà sempre polarità +1 mentre ?A l'avrà −1.
Per quanto riguarda le regole d'identità, l'assioma di identità verrà ristretto alla zona lineare mentre si avranno tre regole del taglio:
Passiamo ora al gruppo strutturale. Qui avremo una regola di scambio senza restrizioni e due serie di quattro regole ciascuna per lo scambio senza restrizioni, l'indebolimento e la contrazione nella zona classica, la possibilità di passare nella zona classica e (con restrizioni di polarità molto forti) la possibilità del passaggio nell'altro senso:
Non daremo le regole del gruppo logico che sono formulate in modo da introdurre connettivi a destra e a sinistra della parte lineare. Questa modifica cambia completamente il comportamento del calcolo e lo migliora rispetto ai calcoli abituali.
I connettivi lineari ci servono per formulare le condizioni del passaggio delle formule da un settore a un altro: !A sarà positiva e ?A sarà negativa. Porremo così le regole:
La novità di LU non sta nella validità dell'Hauptsatz (che ovviamente è dimostrabile) ma nei nuovi rapporti che ha con LK ed LJ, che risultano suoi frammenti: LK, il frammento classico, in cui ci si limita alle polarità +1 e −1 e ai connettivi e quantificatori classici; LJ, il frammento intuizionista, in cui le sole polarità sono 0 e +1 e gli operatori logici solo quelli intuizionisti; il frammento intuizionista neutro, in cui ci si limita alla polarità 0 e si considerano solo i connettivi , ⊃ e il quantificatore universale intuizionista. Ultimo è il frammento lineare che utilizza tutte le polarità e i connettivi lineari. Entro LU i vari frammenti comunicano tra loro ed è possibile quindi dimostrare da teoremi classici corollari intuizionisti o viceversa; d'altra parte il principio della sottoformula ci garantisce che un sequente fatto di formule di un frammento sarà dimostrabile ‒ se dimostrabile ‒ con sequenti dello stesso frammento. Ciò permette di stabilire facilmente relazioni tra LK e LJ: se un sequente Γ;Γ′⇒Δ′;Δ del frammento classico è dimostrabile, avremo anche un teorema Γ;Γ′⇒Δ′;Δ di LK e un sequente Γ;Γ′⇒A del frammento intuizionista diviene un teorema Γ;Γ′⇒A di LJ. Analogo il caso dei passaggi all'inverso. Ciò che ci dà in più l'immersione di LK e LJ in LU è che in questo contesto emergono le dipendenze lineari presenti in teoremi che non contengono connettivi lineari e queste dipendenze permettono di rendere lo Hauptsatz in un certo senso determinista, cosa che non si verifica per LK.
L'esistenza di un sistema come LU cambia profondamente la percezione della diversità della logica. Si tendeva a pensare che esistono tante logiche, ora si può sostenere che ne esiste una sola ma che ci sono tanti connettivi differenti. Si può quindi immaginare l'evoluzione di un quadro come LU verso un sistema gigantesco, con migliaia di connettivi differenti, dove ciascuno sia in grado di utilizzare il proprio frammento. Il vantaggio sta nel fatto che i risultati ottenuti, scritti nello stesso linguaggio, potranno liberamente interagire.
Bibliografia
Buchholz 1981: Buchholz, Wilfried e altri, Iterated inductive definitions and subsystems of analysis: recent proof theoretic studies, Berlin, Springer, 1981.
Buchholz, Schutte 1988: Buchholz, Wilfried - Schutte, Kurt, Proof theory of inpredicative systems, Napoli, Bibliopolis, 1988.
Buss 1998: Handbook of proof theory, edited by Samuel Buss, Amsterdam-Oxford, Elsevier, 1998.
Feferman 1988: Feferman, Salomon e altri, in: "Journal of symbolic logic", 53, 1988 (numero monografico dedicato all'eredità del Programma di Hilbert, con contributi di autori diversi).
Gentzen 1969: Gentzen, Gerhard, The collected papers, ed-ited by M.E. Szabo, Amsterdam, North Holland, 1969.
Gödel 1986-2003: Gödel, Kurt, Collected works, edited by Salomon Feferman e altri, New York, Oxford University Press, I-V, 1986-2003.
Herbrand 1968: Herbrand, Jacques, Ecrits logiques, edited by Jean van Heijenoort, Paris, Presses Universitaires de France, 1968.
Hilbert, Bernays 1934-1939: Hilbert, David - Bernays, Paul, Grundlagen der Mathematik, Berlin, Springer, I-II, 1934-1939.
Girard 1987: Girard, Jean-Yves, Proof theory and logical complexity, Napoli, Bibliopolis, 1987.
Girard 1989: Girard, Jean-Yves, Proof theory and types, Cambridge, Cambridge University Press, 1989.
Girard 1995: Advances in linear logic, edited by Jean-Yves Girard, Yves Lafont, Laurent Regnier, Cambridge, Cambridge University Press, 1995.
Hendricks 2000: Proof theory, edited by Vincent F. Hendricks, Stig A. Pedersen, Klaus F. Jørgensen, Dordrecht, Kluwer Academic, 2000.
Prawitz 1965: Prawitz, Dag, Natural deduction, Stockholm, Almqvist & Wiksell, 1965.
Schutte 1977: Schutte, Kurt, Proof theory, Berlin, Springer, 1977.
Sorensen, Urzyczyn 2006: Sorensen, Morten - Urzyczyn, Pawel, Lectures on the Curry-Howard isomorphism, Amsterdam, Elsevier, 2006.
Takeuti 1986: Takeuti, Gaisi, Proof theory, 2. ed., Amsterdam, North-Holland, 1986.
Troelstra 1993: Troelstra, Anne S., Mathematical investigations of intuitionistic arithmetic and analysis, 2. ed., Amsterdam, Institute for Logic, Language and Computation, 1993.