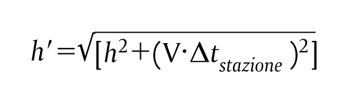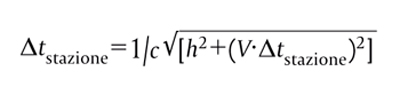relativita, teoria della

relatività, teoria della

Dal tempo assoluto di Galilei allo spazio-tempo di Einstein

La teoria della relatività formulata da Albert Einstein, prima nella sua versione ristretta e poi in quella generale, ha modificato profondamente la teoria della relatività galileiana e ha cambiato il nostro concetto di tempo e di spazio. Per quanto sorprendenti, le previsioni di Einstein hanno ottenuto numerose conferme. Sempre alla relatività dobbiamo l’equazione più famosa della fisica: E = mc²

Il dilemma del viaggiatore

Immaginiamo di essere il passeggero di un treno fermo in stazione e di osservare dal finestrino un altro convoglio che attende di partire sul binario vicino. A un tratto ci accorgiamo che questo secondo treno si sta allontanando. D’istinto, per essere certi che sia l’altro treno a muoversi e non il nostro, cercheremo un riferimento sulla cui immobilità non abbiamo dubbi, per esempio il marciapiede della stazione o un cartello segnaletico. Ma se fosse notte e fosse visibile solo l’altro convoglio e non la stazione? In quel caso non sarebbe affatto facile stabilire quale dei due treni è partito: il moto non è un concetto valido in senso assoluto, ma è sempre relativo all’osservatore che lo considera.

Per studiare un corpo in movimento dobbiamo munirci di un metro e di un orologio, scegliere un punto di riferimento e una terna di assi orientati nello spazio che partono dal punto, rispetto ai quali misurare le distanze; dobbiamo infine stabilire un istante iniziale rispetto a cui misurare gli intervalli di tempo. Per il passeggero che vuole capire se il suo treno è partito o meno, la stazione è un buon riferimento, ma se dovesse descrivere il movimento di una biglia che rotola sul pavimento del vagone su cui viaggia troverebbe molto più comodo scegliere un riferimento fermo rispetto al pavimento.

Sulla nave di Galileo

Abbandoniamo, almeno momentaneamente, il treno per salire a bordo di una nave. Si tratta del «gran navilio» descritto da Galileo Galilei nel Dialogo sopra i due massimi sistemi del mondo. La nave galileiana si muove a velocità costante e non subisce scossoni né effettua brusche virate. Se i passeggeri non guardano fuori dagli oblò non possono capire da semplici esperimenti, come lanciare una biglia sul pavimento, se la nave si sta muovendo rispetto alla Terra oppure è ferma: la biglia va in linea retta esattamente come farebbe sulla terraferma, perché sulla nave che procede a velocità costante seguendo una traiettoria rettilinea le leggi della meccanica conservano piena validità. In particolare, è valido il primo principio della dinamica, o principio d’inerzia, e per questa ragione la nave è un sistema di riferimento inerziale (forza).

Galileo formulò le leggi che legano tra loro le coordinate dei corpi in moto nei riferimenti inerziali, dette trasformazioni di Galileo: esse mostrano come si trasformano le coordinate spaziali di un corpo quando si passa da un riferimento inerziale a un altro, e si basano sull’ipotesi che il tempo sia una grandezza universale, cioè che tutti gli orologi, una volta sincronizzati, continuino a camminare con lo stesso passo indipendentemente dal riferimento in cui si trovano.

Ben diversa è invece la situazione in presenza di una tempesta: la nave oscilla a causa delle onde, fa virate improvvise e i passeggeri potrebbero facilmente stabilire che si sta muovendo, anche senza guardare fuori. La nave, in questo caso, costituisce un sistema accelerato, o non inerziale, perché in esso non vale il principio d’inerzia e la traiettoria della biglia lanciata sul pavimento non sarebbe certamente rettilinea.

In treno con Albert Einstein

Nuovi principi per la relatività. Torniamo sul treno e lasciamo che a condurlo sia un macchinista d’eccezione: Albert Einstein. Einstein formulò una nuova teoria della relatività basata su due principi: il primo è che le leggi della fisica non cambiano quando si passa da un riferimento inerziale a un altro; il secondo è che la velocità della luce nel vuoto, indicata con c (vale circa 300.000 km/s), è la stessa per qualsiasi osservatore, fermo o in movimento, è indipendente dalla velocità della sorgente ed è la massima velocità raggiungibile. Le conseguenze di questa affermazione hanno cambiato radicalmente i nostri concetti di tempo e spazio; vediamo perché.

Un esperimento ideale. Supponiamo che sul soffitto di un vagone del treno ci sia una lampadina che invia un impulso luminoso a un sensore posto sul pavimento, direttamente sotto la lampadina. Un osservatore sul treno misura l’intervallo di tempo (indicato come ∆t_treno) che passa tra l’emissione dell’impulso e la sua ricezione da parte del sensore. Se h è l’altezza del vagone si avrà che ∆t_treno =h/c. Il treno sta transitando per una stazione con velocità costante V rispetto alla banchina. Come descriverà la scena un osservatore fermo sulla banchina? Anch’egli vedrà la luce raggiungere il sensore, e con il suo orologio misurerà un tempo che chiamiamo ∆t_stazione. Rispetto a questo osservatore l’impulso luminoso percorre non solo il tratto verticale h, ma anche un tratto orizzontale ∆x=V ∆t_stazione perché il treno nel frattempo si sta muovendo. L’impulso compie quindi un percorso complessivo h', che per il teorema di Pitagora è

Siccome la luce ha velocità c anche nel riferimento dell’osservatore sulla banchina, il tempo che impiega per raggiungere il sensore è ∆t_stazione = h'/c, cioé

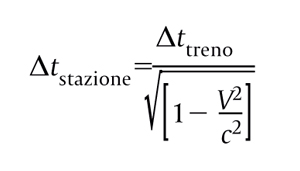
Basta adesso sostituire in questa equazione h = c ∆t_treno per trovare che

Cambiano il tempo e lo spazio. Dalla precedente equazione emerge un fatto rivoluzionario: l’intervallo di tempo misurato dall’orologio dell’osservatore in movimento è diverso da quello misurato dall’orologio a terra! E l’effetto è tanto più marcato quanto più la velocità del treno si avvicina a quella della luce, perché il rapporto V²/c² tende a 1 e il denominatore dell’equazione diventa così sempre più piccolo; di conseguenza aumenta il valore di ∆t_stazione. A questo fenomeno, noto come dilatazione dei tempi, si accompagna invece la contrazione delle lunghezze nella direzione di moto. Se, infatti, l’osservatore sulla banchina misurasse quanto è lungo il treno in marcia, otterrebbe un valore inferiore a quello misurato dal passeggero che si trova sul convoglio. Questi risultati sono conseguenza delle trasformazioni di Lorentz (di cui la formula precedente è un esempio) che hanno sostituito quelle di Galilei nella teoria della relatività ristretta. Secondo questa teoria, nel passare da un riferimento inerziale all’altro, sia le coordinate spaziali sia quelle temporali cambiano, mentre nelle trasformazioni di Galilei il tempo è sempre lo stesso, indipendentemente dal riferimento scelto. I corpi, dunque, si muovono nello spazio-tempo, perché spazio e tempo risultano indissolubilmente legati. La posizione di un corpo a un dato istante di tempo rispetto a un riferimento inerziale è un evento dello spazio-tempo e le trasformazioni di Lorentz permettono di trovare le coordinate di quell’evento rispetto a un qualsiasi altro riferimento inerziale.

A bordo di un’astronave

Sempre al seguito di Albert Einstein proseguiamo il nostro viaggio, ma ora su un’astronave che si sta avvicinando alla Terra a motori ancora spenti, di ritorno da un viaggio spaziale. Nel 1907 Einstein formulò quello che definì «il pensiero più felice della mia vita»; comprese cioè che per un osservatore in caduta libera (per esempio, l’astronauta all’interno della navicella) la gravità scompare. Ciò significa che se, all’interno dell’astronave, si lasciasse libera di muoversi una palla, questa non cadrebbe, ma rimarrebbe ferma rispetto alle pareti. L’astronave in caduta libera è quindi un riferimento localmente inerziale: se si lancia una biglia sul pavimento, questa avanza in linea retta perché vale il principio d’inerzia come sulla nave di Galileo. Il termine localmente significa che questa proprietà è valida nello spazio limitato dell’astronave, e per un intervallo di tempo piccolo, per esempio, rispetto a quello che la navicella impiega per raggiungere il suolo. Possiamo quindi formulare il principio di equivalenza: in un riferimento localmente inerziale le leggi della fisica devono avere la stessa forma che le contraddistingue nella teoria della relatività ristretta, cioè la stessa forma che avrebbero in assenza di gravità. Basandosi su questo principio, Einstein formulò le equazioni che stanno alla base della teoria della relatività generale: queste equazioni descrivono il campo gravitazionale e valgono in un riferimento qualsiasi, inerziale e non inerziale.

La gravità curva lo spazio-tempo

Se in un riferimento in caduta libera la gravità scompare, come possiamo capire se stiamo precipitando in un campo gravitazionale oppure no? Supponiamo di trovarci sull’astronave e di disporre di due sfere. Lasciamole libere per un poco: come abbiamo visto prima, esse rimarranno ferme. Se però attendiamo per un tempo sufficientemente lungo, poiché il campo gravitazionale è diretto verso il centro della Terra e quindi varia mentre l’astronave cade, vedremo che i due corpi si avvicinano tra loro in direzione orizzontale. Da questo deduciamo che stiamo cadendo verso la Terra e che è opportuno accendere i motori per frenare la caduta!

Le traiettorie nello spazio-tempo dei due corpi che si avvicinano non dipendono dalla loro massa: anche se le masse fossero molto più piccole (o più grandi), non cambierebbero. La gravità, quindi, determina le traiettorie che tutti i corpi lasciati liberi di muoversi devono seguire. Se non c’è gravità queste traiettorie sono rette, ma se è presente diventano curve, e se confrontiamo due traiettorie vicine vedremo che la loro distanza varia nel tempo a seconda di come è fatto il campo gravitazionale nel quale sono immerse: è per questo motivo che diciamo che la gravità curva lo spazio-tempo.

Alcune importanti conseguenze della relatività generale

Un raggio di luce che passa vicino a una stella non prosegue in linea retta, ma viene deviato. Infatti la luce è energia, e poiché massa ed energia sono equivalenti (E = mc²) la luce sarà attratta da una stella così come lo sarebbe una massa. Questo fenomeno fu osservato per la prima volta nel 1919 dall’astronomo inglese Sir Arthur Eddington, che misurò durante un’eclissi di Sole come i raggi provenienti da stelle poste dietro il Sole fossero deviati dal suo campo gravitazionale. Molti altri effetti predetti dalla teoria di Einstein sono stati verificati, per esempio la precessione del perielio di Mercurio, ovvero lo spostamento nel tempo del punto in cui questo pianeta si avvicina di più al Sole, e lo spostamento verso il rosso della radiazione emessa dalle sorgenti che si trovano in campi gravitazionali molto intensi (redshift gravitazionale).

La teoria prevede anche l’esistenza dei buchi neri e delle onde gravitazionali. Le osservazioni astronomiche indicano che al centro di molte galassie c’è un buco nero di massa pari a milioni (o miliardi) di volte quella del Sole. Le onde gravitazionali sono state per ora rivelate solo indirettamente, studiando (e misurando) l’effetto che la loro emissione produce sull’orbita di sistemi binari, formati da due stelle di neutroni molto vicine tra loro; grazie, però, a speciali antenne, collocate a terra e nello spazio, si cercherà di rivelarle anche direttamente.

L’equazione più famosa

Nell’articolo del 1905, in cui Albert Einstein espone i fondamenti della relatività ristretta, fa la sua prima comparsa anche la formula E = mc², destinata a diventare l’equazione per eccellenza della fisica. Essa stabilisce che se un corpo emette un’energia E sotto forma di radiazione, la sua massa m diminuisce di una quantità E /c², quindi massa ed energia possono trasformarsi l’una nell’altra. Questo avviene per esempio nei decadimenti radioattivi o nelle reazioni nucleari. L’equazione E = mc² dice anche che una piccolissima massa può trasformarsi in una enorme quantità di energia, perché il fattore c² vale 9 x 10¹⁶. Per esempio, così si spiega perché una stella possa splendere per miliardi di anni trasformando, attraverso le reazioni nucleari, una piccolissima parte della sua massa in un’enorme quantità di energia.