Decisioni, teoria delle
Decisioni, teoria delle
Introduzione
Lo studio sistematico dei processi decisionali è stato avviato e messo a punto nel XX secolo. Le tre pietre miliari del suo sviluppo sono state: la nascita della moderna teoria dell'utilità, l'elaborazione della teoria dei giochi e la costruzione di un modello teorico per lo studio delle scelte collettive. Mentre alla formulazione della teoria dell'utilità hanno contribuito molti studiosi, la teoria dei giochi e quella delle scelte collettive risalgono, rispettivamente, a John von Neumann e a Kenneth Arrow. Da un determinato punto di vista la teoria delle decisioni può essere suddivisa in teoria normativa e teoria comportamentale. La prima indica come ci si deve comportare per agire razionalmente; la seconda studia il modo in cui, di fatto, vengono prese le decisioni. Da un altro punto di vista le varie componenti della teoria delle decisioni possono essere classificate in base a tre distinzioni: 1) la situazione di scelta può essere caratterizzata da informazione completa o incompleta; 2) il contesto in cui le decisioni vengono prese può essere assunto come dato ('parametrico') o come strategico (nel primo caso il soggetto non si deve preoccupare di ciò che gli altri faranno in conseguenza o in previsione delle sue azioni; nel secondo le decisioni saranno interdipendenti); 3) le decisioni possono essere individuali o collettive.
Razionalità, preferenze, utilità
Agire razionalmente significa agire nel modo migliore possibile rispetto a un fine. Questa semplice definizione evidenzia le due nozioni centrali insite nel concetto di razionalità. Infatti la scelta razionale da un lato è limitata dalla fattibilità (il consumatore non può comprare più di quanto il suo bilancio gli consenta), dall'altro è guidata dal perseguimento dell'ottimalità. Nei limiti delle sue possibilità il consumatore acquista il prodotto o l'insieme di prodotti che preferisce. Nella teoria classica della scelta razionale si postula, generalmente, che i due elementi - l'insieme delle alternative accessibili e le preferenze - siano indipendenti l'uno dall'altro, ma talvolta tra di loro sussistono nessi causali: l'insieme delle alternative accessibili può essere plasmato in base alle preferenze, come nella storia di Ulisse e delle sirene, o viceversa, come nella favola della volpe e dell'uva. Infine le preferenze e le alternative accessibili possono essere effetti di una stessa causa, come nel caso della democrazia americana, che, secondo quanto ha osservato Tocqueville, attribuisce ampi poteri al Presidente, riducendone, nel contempo, il desiderio di usarli. Questo modello va completato sotto due aspetti. In primo luogo le decisioni non sono determinate direttamente dall'insieme delle alternative accessibili, ma dalle convinzioni del soggetto al riguardo, cioè dal grado di probabilità (fino al limite della certezza) che egli annette alla attuabilità delle diverse linee di condotta. Inoltre le preferenze, il più delle volte, non si formano direttamente in funzione delle azioni, bensì dei loro risultati, e anche nella valutazione dei risultati entrano in gioco le convinzioni. Quindi, perché un'azione sia razionale, è necessario che le convinzioni sulle quali si fonda siano anch'esse razionali.
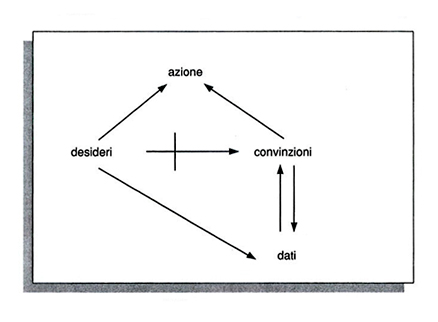
Per convinzione razionale si intende un'opinione ben fondata sui dati di fatto a disposizione del soggetto (esempi di opinioni non ben fondate sono forniti nel cap. 8). Chi agisce in modo razionale, inoltre, deve raccogliere una quantità ottimale di dati empirici prima di formarsi le proprie convinzioni. Ogni decisione di agire è accompagnata da una 'decisione ombra' sul momento in cui smettere di raccogliere dati empirici. Quanti dati sia razionale raccogliere dipende in parte dall'obiettivo del soggetto e in parte dalle sue precedenti convinzioni circa i costi della raccolta di informazioni e i benefici che può trarne. La fig. 1 illustra la struttura dell'azione razionale. Questa comporta tre operazioni di ottimizzazione: dati determinati desideri e determinate convinzioni, individuare la migliore linea di condotta; date determinate informazioni empiriche, formarsi l'opinione più fondata; dati determinati desideri e convinzioni precedenti, raccogliere la quantità giusta di informazioni empiriche. Qui i desideri sono 'motori immobili', conformemente a quanto affermava David Hume, per il quale "la ragione è e non può non essere schiava delle passioni". Con ciò Hume non voleva dire che la ragione deve obbedire ai capricci e alle stravaganze delle passioni. In particolare, egli avrebbe rifiutato l'idea che la ragione sia plasmata direttamente da una passione fondata su un mero desiderio (v. la 'freccia sbarrata' nella fig. 1). Per servire bene il proprio padrone uno schiavo deve possedere un certo margine di autonomia di esecuzione: le convinzioni che nascono dalla passione sono per essa cattivi servitori. Gli obiettivi o i desideri dell'agente sono definiti dal suo insieme di preferenze nei riguardi delle scelte che gli si prospettano. Noi distinguiamo tra preferenza debole ('buono almeno quanto') e preferenza forte ('migliore di, in senso stretto'). Un insieme di preferenze è completo se, per ogni coppia di scelte, a e b, il soggetto ha una preferenza debole o per a rispetto a b o per b rispetto ad a (se ha una preferenza debole sia per a rispetto a b sia per b rispetto ad a, è indifferente a entrambe). Le preferenze si dicono coerenti (o transitive) se, per ogni terna, a, b e c, una preferenza debole per a rispetto a b e una preferenza debole per b rispetto a c implicano una preferenza debole per a rispetto a c. Le preferenze sono dette continue se, per ogni scelta a, l'insieme di tutti gli oggetti buoni almeno quanto a e l'insieme degli oggetti non migliori di a sono entrambi chiusi. In altre parole, se tutte le scelte in una successione convergente sono buone almeno quanto a (non migliori di a), allora anche il limite della successione è buono almeno quanto a (non migliore di a). Un esempio ben noto di preferenze non continue è l'ordinamento lessicografico. Si supponga che gli analcolici siano descritti secondo due dimensioni: il prezzo e il contenuto calorico. Si ha un ordinamento lessicografico quando la bevanda a è preferita alla bevanda b se e solo se o costa meno di b o - a parità di prezzo - ha meno calorie di b. Requisito fondamentale del comportamento razionale è che le preferenze siano coerenti, mentre non è necessario che siano complete e continue.Il rapporto tra utilità, preferenza e scelta può essere definito in vari modi. Nella teoria classica, che risale a Jeremy Bentham, l'utilità è concepita come il grado di piacere o di dispiacere associato a un oggetto o a un'esperienza; pertanto l'utilità è prioritaria rispetto alle preferenze: un soggetto preferisce a a b perché trae maggiore utilità da a che da b, e quindi, potendo scegliere, sceglierà a. Le teorie dell'utilità moderne danno la priorità alle preferenze rispetto all'utilità. Se le preferenze sono complete, coerenti e continue, possono essere rappresentate da una funzione di utilità ordinale, u, che, date due scelte, a e b, assegna loro due numeri reali, rispettivamente u(a) e u(b), tali che u(a) > u(b) se e solo se a è preferito a b in senso stretto. In questa formulazione l'utilità non rappresenta un'esperienza soggettiva, ma è solo una comoda convenzione matematica per indicare le preferenze. I numeri che rappresentano l'utilità possono essere scelti arbitrariamente, purché rispettino la gerarchia ordinale delle alternative (cioè l'ordine secondo cui sono classificate). Questo concetto di utilità è chiamato, pertanto, 'utilità ordinale'. La funzione ordinale non ci permette di misurare l'intensità delle preferenze, né, quindi, per esempio, di definire il concetto di utilità marginale decrescente. Secondo la teoria delle preferenze rivelate, la possibilità di scelta condiziona le preferenze: dire che 'a è preferito a b' significa che a viene scelto quando anche b è disponibile. Secondo altre teorie, le preferenze precedono le scelte e le determinano: a viene scelto quando anche b è disponibile perché a è preferito a b. La teoria della scelta razionale si propone di spiegare il comportamento, ma può fallire l'obiettivo in due modi. In primo luogo può non essere in grado di fornire regole e previsioni di comportamento univoche. Tra le fonti di tale indeterminazione vi sono l'incertezza assoluta (v. cap. 4) e l'incertezza strategica (v. cap. 5). In secondo luogo il comportamento degli individui può non conformarsi alle regole e alle previsioni della teoria. Alcune di queste anomalie saranno trattate nel cap. 8.
Decisioni parametriche in condizioni di informazione completa
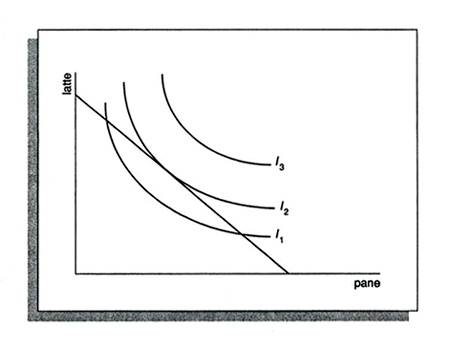
Quando le preferenze possono essere rappresentate mediante una funzione di utilità, si può ricorrere al diagramma delle curve di indifferenza.
Nella fig. 2, I₁, I₂ e I₃ sono curve di indifferenza. Il consumatore è indifferente nei confronti di due qualsiasi combinazioni di pane e latte che giacciano sulla stessa curva. Le curve sono tracciate in modo da riflettere il fatto, comunemente osservato, che il consumatore, a mano a mano che acquista quantità via via minori di pane, per restare allo stesso livello di soddisfazione dovrà compensarle con quantità sempre crescenti di latte. Il saggio di sostituzione (o tradeoff) fra latte e pane dipende dalle quantità di questi due beni che il consumatore possiede già. Supponendo che il consumatore preferisca sempre quantità maggiori a quantità minori, egli preferirà un qualsiasi punto di I₃ a un qualsiasi punto di I₂ e un qualsiasi punto di I₂ a un qualsiasi punto di I₁. La retta della spesa mostra tutte le combinazioni di pane e latte che il consumatore può permettersi di acquistare con una data spesa. L'inclinazione di questa retta dipende dai prezzi relativi del pane e del latte. Il consumatore sceglierà di acquistare la combinazione accessibile che giace sulla curva di indifferenza più alta, cioè quella corrispondente al punto in cui la I₂ è tangente alla retta della spesa. Tecniche simili possono essere usate per studiare le combinazioni di fattori produttivi scelte da un produttore. In questo caso il concetto di curva di indifferenza viene sostituito con quello di isoquanto, definito come il luogo dei punti corrispondenti a tutte le combinazioni di fattori produttivi che consentono di ottenere la stessa quantità di prodotto finale.
Un problema fondamentale sorge quando le conseguenze delle scelte attuali sono differite nel tempo. Supponiamo che si debba scegliere fra due diverse carriere. La prima assicura guadagni più cospicui nell'arco della vita, ma richiede anche maggiori sacrifici immediati. In questo caso molti sceglieranno la seconda opportunità di carriera, dimostrando una preferenza per un reddito presente e nel futuro immediato rispetto a un reddito nel lontano futuro. Fino a un certo punto queste scelte possono essere spiegate con la presenza di un rischio. È ragionevole, infatti, non tener conto di un reddito futuro, poiché si potrebbe non vivere abbastanza per goderne. Entro certi limiti queste scelte possono essere spiegate anche facendole risalire alla previsione di un mutamento di gusti e di bisogni. È ampiamente dimostrato, tuttavia, che i vantaggi presenti vengono preferiti a quelli futuri al di là delle motivazioni razionali che giustificano tale scelta. Esiste un elemento di pura preferenza temporale: si preferisce il presente semplicemente perché è più vicino al momento della decisione. Non tutti sono d'accordo sul carattere irrazionale della pura preferenza temporale. Alcuni affermano che una preferenza non può essere né razionale né irrazionale, poiché de gustibus non est disputandum. Altri sostengono che la preferenza temporale non può essere razionale se conduce a un comportamento autodistruttivo e all'assuefazione. Alcuni tipi di preferenza temporale sono, comunque, indiscutibilmente irrazionali: sono quelli che si manifestano quando il soggetto è incapace di tener fede a una sua precedente decisione, in quanto l'importanza relativa di momenti futuri differenti cambia a mano a mano che questi si avvicinano. Un individuo può telefonare al dentista il 1° gennaio per prendere un appuntamento per il 15 febbraio, e poi chiamarlo di nuovo il 14 febbraio per annullare l'appuntamento solo per la paura del dolore imminente. Per prevenire tale comportamento, si potrebbe autorizzare il dentista a raddoppiare l'onorario normale per ogni appuntamento annullato. Tali strategie di controllo sono riscontrabili in molti comportamenti umani e persino animali.
Decisioni parametriche in condizioni di rischio e di incertezza
Le decisioni in condizioni di informazione incompleta possono essere ulteriormente suddivise in decisioni in condizioni di rischio e decisioni in condizioni di incertezza. Nel primo caso il soggetto è in grado di assegnare determinate probabilità alle possibili eventualità. Nel secondo egli sa così poco della situazione che non è in grado di fare neppure questo. Si tratta, in tal caso, di incertezza assoluta, derivante da una completa ignoranza di dati di fatto del tutto indipendenti dal processo decisionale; altra cosa è l'incertezza strategica, dovuta all'interazione fra gli agenti.
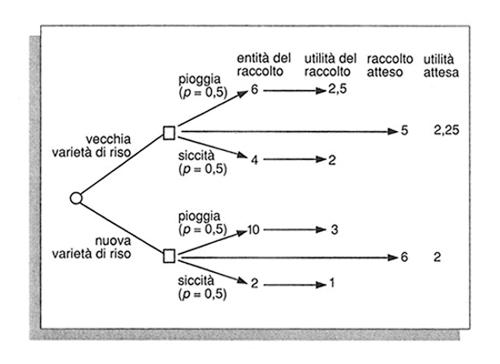
Le decisioni parametriche in condizioni di rischio sono guidate dal criterio della massimizzazione dell'utilità attesa. Questo criterio si basa sul concetto di 'utilità cardinale' (un concetto più forte di quello illustrato poco fa, di 'utilità ordinale'), il quale consente di formulare in termini matematici le preferenze in caso di esiti soggetti a rischio. Supponiamo che a sia un esito molto positivo e b un esito molto negativo, cui assegniamo, arbitrariamente, utilità 1 e utilità 0, rispettivamente. Dato un qualsiasi esito c, compreso fra a e b, si definisce utilità cardinale di c quel numero, pc, tale che per il soggetto è indifferente ottenere c per certo oppure correre l'alea di ottenere a con probabilità pc e b con probabilità (1 - pc). Contrariamente all'utilità ordinale, l'utilità cardinale permette di misurare e confrontare intensità di preferenze: il fatto che la preferenza di un soggetto per x rispetto a y sia più forte della sua preferenza per u rispetto a v si traduce nella formula (px - py) > (pu - pv). La verità di questa disuguaglianza non dipende dai numeri arbitrari assegnati ad a e a b. I valori numerici dell'utilità cardinale riflettono sia l'intrinseca attrattiva delle alternative sia l'atteggiamento del soggetto nei confronti del rischio: avversione al rischio, indifferenza nei riguardi del rischio, propensione al rischio; per questo motivo non costituiscono una misura del tutto valida dell'intensità delle preferenze. Tuttavia essi sono largamente impiegati in virtù della seguente proprietà: l'utilità attesa di una scelta a rischio è pari alla media pesata delle utilità dei possibili esiti, ciascuna moltiplicata per la rispettiva probabilità. Si consideri, per esempio, un contadino che debba scegliere tra due varietà di riso, sapendo che nell'anno successivo pioggia e siccità hanno la stessa probabilità (50%) di verificarsi (v. fig. 3). La vecchia varietà di riso è affidabile ma di basso rendimento, mentre la nuova dà ottimi risultati in caso di pioggia, pessimi in caso di siccità. Il raccolto medio, o atteso, della nuova varietà è di 6 unità, mentre quello della vecchia è di 5 unità. I contadini, però, non possono vivere di un raccolto medio. Se, per esempio, il livello di sussistenza corrisponde a un raccolto di 4 unità, la nuova varietà di riso ridurrebbe il contadino alla fame ogni due anni, in mancanza di risparmi individuali, granai comunali o sussidi statali. Qualsiasi contadino che si comporti razionalmente sceglierebbe la vecchia varietà di riso. Più in generale, se il riso ha, per il contadino, un'utilità marginale decrescente (v. fig. 3), la vecchia varietà di riso massimizza l'utilità media o attesa. Ciò che il contadino massimizza è l'utilità attesa del raccolto, non l'utilità del raccolto atteso. In altri termini, i contadini tendono, per buone ragioni, ad essere avversi al rischio.
In questo caso è ragionevole supporre che il contadino sia in grado di assegnare le probabilità con una certa precisione, basandosi sull'esperienza maturata nelle stagioni precedenti. In altri casi, invece, non è ragionevole presumere che il contadino sia in grado di assegnare precise probabilità numeriche ai vari eventi che potrebbero influire sui suoi progetti. Supponiamo, per esempio, che il contadino produca per il mercato e sia tenuto a corrispondere una determinata quota allo Stato. Egli potrebbe temere che, se adotta una nuova varietà di riso e ne ricava un ottimo raccolto, lo Stato aumenti la quota, lasciandolo in condizioni finanziarie non migliori di quelle ottenibili con la vecchia varietà. Ma il contadino raramente è in grado di assegnare una probabilità numerica a questo intervento dello Stato. Tutto quello che sa è che un'eventualità del genere potrebbe verificarsi - perché fatti analoghi sono avvenuti in passato - o non verificarsi - poiché il governo ha promesso che non modificherà le quote. Il contadino, quindi, si trova ad affrontare una decisione in condizioni di incertezza. In queste circostanze una regola (ma non l'unica) che è ragionevole seguire nel prendere la decisione consiste nel 'criterio del massiminimo': per ogni possibile linea di condotta si individua il peggior esito possibile e quindi si sceglie la linea di condotta che porta alla migliore fra le conseguenze peggiori (si sceglie, cioè, il male minore). Il contadino, quindi, non agisce irrazionalmente se, in una situazione di incertezza, adotta questo criterio di cautela; d'altra parte, questa non è l'unica scelta razionale.
Decisioni strategiche in condizioni di informazione completa
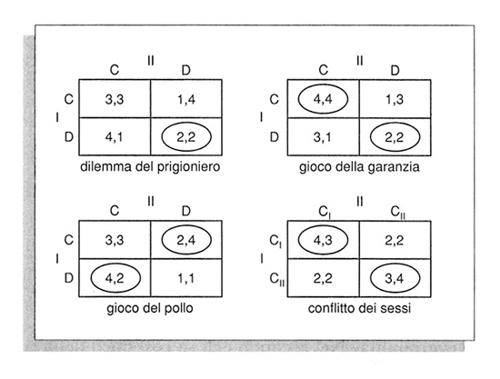
La struttura dell'interazione strategica è la seguente: vi sono n (n ≥ 2) agenti o giocatori; ciascuno di essi ha la possibilità di scegliere tra diverse azioni o strategie; a ogni combinazione di n strategie (una strategia per ciascun giocatore) corrisponde un determinato risultato, cui ciascun giocatore attribuisce un'utilità cardinale. Il problema, per ogni giocatore, è quello di individuare la strategia che massimizzerà la sua utilità attesa, sapendo che anche gli altri giocatori cercheranno di massimizzare la propria utilità attesa. Per indicare le soluzioni di questo insieme di problemi di massimizzazione si deve prima definire il concetto di insieme di strategie di equilibrio: l'insieme delle strategie tali che nessun agente può conseguire un risultato per sé più favorevole cambiando unilateralmente la propria strategia. Le strategie di equilibrio costituiscono le risposte reciproche ottimali. Tutti i giochi caratterizzati da insiemi di strategie compatti e chiusi hanno almeno un punto di equilibrio. Quando esiste un punto di equilibrio, esso costituisce ipso facto la soluzione. Quando vi sono diversi punti di equilibrio e uno di questi è debolmente preferito da tutti e fortemente preferito da alcuni, rispetto a tutti gli altri punti, allora esso diventa la soluzione. Infine un punto di equilibrio può diventare la soluzione se può essere sostenuto con minacce credibili. Alcuni giochi, comunque, non hanno soluzione. Tra i giochi trattati sotto non hanno soluzione il 'gioco del pollo' e il 'conflitto dei sessi'.I giochi sono classificati in base a diverse caratteristiche. Esistono giochi di conflitto puro (giochi a somma zero), giochi di pura cooperazione e giochi misti, che comportano sia conflitto sia cooperazione. Quasi tutti i giochi del mondo reale sono misti. I giochi, poi, possono essere a due persone o, più in generale, a n persone; un aspetto importante dei giochi a n persone è la possibilità di formare coalizioni. I giochi fondati sulla cooperazione sono caratterizzati dalla possibilità di fare promesse vincolanti. La fig. 4 mostra alcuni esempi importanti di giochi che prevedono sia il conflitto sia la cooperazione. Quanto precisato qui per il caso a due persone può essere esteso, attraverso ovvie analogie, al caso a n persone.In ogni gioco vi sono due giocatori, I e II. Ciascuno di essi può scegliere fra due strategie. Nel 'dilemma del prigioniero', nel 'gioco della garanzia' e nel 'gioco del pollo' le due strategie sono la cooperazione (C) e la defezione (D); nel 'conflitto dei sessi' esse sono la coordinazione con i presupposti di I (CI) e la coordinazione con i presupposti di II (CII). Ad ogni coppia di strategie (una strategia per ciascun giocatore) corrisponde un determinato risultato. Le utilità cardinali dei vari risultati per I e per II, rispettivamente, sono rappresentate dai numeri nelle caselle: il primo numero rappresenta l'utilità per I, il secondo l'utilità per II. In ogni gioco i punti di equilibrio sono cerchiati.
Consideriamo per primo il gioco più noto, il 'dilemma del prigioniero', così chiamato perché basato sulla seguente situazione. La polizia cattura due individui sospettati di un delitto e li rinchiude in due celle distinte; poi a ciascuno dei due, in separata sede, prospetta queste possibilità: se l'uno dà informazioni sull'altro (cioè lo tradisce) e l'altro non dà informazioni su di lui (cioè coopera con lui), il primo verrà liberato, mentre il secondo sarà condannato a dieci anni di prigione; se i due si accusano reciprocamente, entrambi saranno condannati a cinque anni di prigione; se nessuno dei due dà informazioni sull'altro, sconteranno un anno ciascuno. In questo gioco la razionalità individuale non dà luogo al risultato desiderabile da parte di tutti. A prescindere dalla strategia scelta dall'altro, dal punto di vista individuale è razionale tradire. Il tradimento (la defezione) è una strategia dominante, malgrado il fatto che, se tutti e due tradiscono, entrambi ottengono un risultato peggiore di quello che otterrebbero cooperando. Questo dilemma, come dimostrano i seguenti casi, si presenta frequentemente.
Inquinamento: ciascun individuo subisce danni così irrilevanti dalle proprie attività inquinanti che non ritiene valga la pena di astenersene. Negligenza: a meno che i salari non siano strettamente legati alle prestazioni individuali, impegnarsi a fondo nel lavoro comporta benefici tanto esigui che non vale la pena di farlo. Rivoluzione: poiché il singolo individuo non può influenzare la probabilità che scoppi una rivoluzione, ciascuno può preferire che siano gli altri ad assumersene il rischio. Avere figli: per la singola coppia può essere vantaggioso mettere al mondo molti figli, mentre il paese nel suo complesso potrebbe risentire negativamente dell'esistenza di molti nuclei familiari numerosi. Erosione: il singolo contadino può non essere danneggiato dal disboscamento del proprio appezzamento di terreno, mentre il disboscamento di tutti gli appezzamenti potrebbe far perdere la terra a tutti i contadini.
Corruzione: se nessuno ricorresse alla corruzione, la vita economica sarebbe molto più prevedibile e, nel lungo periodo, tutti ne trarrebbero beneficio; tuttavia, nel breve periodo, la corruzione può essere un comportamento razionale dal punto di vista individuale.Le soluzioni di questi dilemmi possono essere centralizzate o decentrate. Da una parte lo Stato può cambiare le regole del gioco, introducendo multe o pene detentive per chi 'tradisce' oppure ricompense per chi coopera con l'altro; i singoli individui, dall'altra parte, possono essere spinti dalla solidarietà, al di là dei propri interessi personali. In entrambi i casi un esito probabile è la trasformazione del 'dilemma del prigioniero' nel 'gioco della garanzia', che ha due punti di equilibrio, che corrispondono alla non cooperazione da parte di tutti e alla cooperazione da parte di tutti. Ciascun individuo pensa: "Io collaborerò se e solo se lo faranno anche gli altri. È giusto che io faccia la mia parte, ma non vedo perché dovrei sacrificarmi quando gli altri non lo fanno". In questo caso il problema dell'informazione diventa cruciale, poiché nessuno coopererà a meno che non abbia buone ragioni di credere che anche gli altri coopereranno.
Anche il 'gioco del pollo' ha due punti di equilibrio, ma, contrariamente al 'gioco della garanzia', nessuno di essi è chiaramente superiore all'altro. Ciascun giocatore preferirà quel punto di equilibrio che lo avvantaggerà maggiormente. Molti problemi di contrattazione presentano questa forma generale. Ogniqualvolta due parti intraprendono insieme un'attività produttiva, sorge il problema della divisione di ciò che producono. Ciascuna parte ha interesse a massimizzare sia il prodotto totale sia la propria quota. Questi due obiettivi spesso suggeriscono strategie differenti. Una delle parti può minacciare di ritirarsi dall'attività comune se non otterrà un'ampia quota. Per rendere credibile la minaccia, potrebbe, per esempio, dichiarare che accettare una quota inferiore comporterebbe una intollerabile perdita di credibilità. In alternativa la parte in questione può investire risorse per accrescere il proprio potere contrattuale, come quando un'industria aumenta le scorte per essere in grado di resistere a uno sciopero. Il problema, comunque, sta nel fatto che l'altra parte può adottare una tattica simile. In tal caso entrambe le parti perdono. Per incrementare le rispettive quote le parti contraenti adottano tattiche che o riducono la probabilità di raggiungere un accordo oppure diminuiscono la quantità totale di prodotto da ripartire. In entrambi i casi si avranno perdite indesiderabili dal punto di vista della società.Il 'conflitto dei sessi' è un problema di coordinazione che ha due punti di equilibrio, caratterizzati dal fatto che nessun agente vorrebbe che un altro agente qualsiasi si discostasse dal comportamento di equilibrio. La cosa più importante è accordarsi su alcuni comportamenti coordinati (perciò si parla di 'equilibri di convenzione'): per esempio, nella guida, o tutti tengano la sinistra o tutti tengano la destra; o, altro esempio, tutti adottino X come lingua ufficiale o tutti adottino Y. A volte non ha importanza quale convenzione venga scelta: per esempio, la posta in gioco non è molto alta quando si tratta di scegliere il nome di una specie di pianta appena scoperta. In altri casi, invece, la scelta della convenzione ha molta importanza. Il 'conflitto dei sessi' rappresenta una situazione in cui ciascun agente preferisce una coordinazione sulla base dei propri presupposti (per esempio che si scelga il suo dialetto come lingua ufficiale). Benché ogni agente preferisca una coordinazione, il conflitto sul punto di coordinazione può impedire il raggiungimento di un accordo. Anche in questo caso ogni parte può cercare di imporre la propria soluzione preferita, e di nuovo il risultato può essere disastroso se tutte le parti adottano questa linea di condotta.
Decisioni strategiche in condizioni di informazione incompleta
La maggior parte dei problemi di contrattazione rientra in questa categoria. Dal momento che l'acquirente e il venditore di una casa non sono a conoscenza l'uno dei prezzi di riserva dell'altro, spesso essi hanno difficoltà a raggiungere un accordo. Inoltre l'acquirente sa che il venditore conosce la casa molto meglio di quanto egli possa arrivare a conoscerla con una breve visita o anche con una minuziosa ispezione. Se compra d'estate, l'acquirente deve in larga misura fidarsi delle parole del venditore circa le condizioni della casa nel periodo invernale. Come suggerisce questo esempio, la distribuzione delle informazioni è doppiamente asimmetrica. In primo luogo ciascuna delle due parti è a conoscenza di elementi soggettivi che l'altra parte ignora, come le proprie preferenze e le informazioni in suo possesso. In secondo luogo vi possono essere informazioni su dati oggettivi che in teoria sono a disposizione di entrambe le parti, in pratica di una sola di esse. Problemi analoghi si presentano nel caso della contrattazione collettiva. La direzione aziendale non conosce il grado di avversione al rischio o il tasso di preferenza temporale del sindacato. Questo, a sua volta, in genere non dispone di informazioni complete sull'effettiva situazione finanziaria dell'impresa.
L'incertezza circa le preferenze presenta molteplici aspetti. In tutti i tipi di contrattazione l'atteggiamento nei confronti del rischio e le preferenze temporali sono fondamentali. Nelle contrattazioni riguardanti pacchetti multidimensionali, possono rivelarsi molto importanti le sostituibilità soggettive, per le diverse parti, dei componenti. Parti contraenti che si incontrino più e più volte finiscono per acquisire molte informazioni l'una sulle preferenze dell'altra; ciò ovviamente non accade nel caso di contrattazioni che si concludono in una sola volta. Ma anche quei contraenti che si conoscono l'un l'altro intimamente possono essere in grado di sfruttare l'incertezza di una terza parte, nel caso in cui controversie irrisolte necessitino di un arbitrato. In tribunale un marito può riuscire a presentarsi come un padre premuroso e capace, benché sia lui sia la moglie sappiano che trascurerebbe il figlio se ne ottenesse l'affidamento; pertanto, in un accordo privato tra le parti, la moglie può essere costretta ad accettare un accomodamento finanziario svantaggioso per ottenere l'affidamento. L'incertezza su dati oggettivi, per quanto sia un problema meno fondamentale, è anch'essa assai diffusa. È più che probabile che il venditore di un tappeto orientale ne sappia molto di più sulla sua qualità della maggior parte dei potenziali acquirenti. In condizioni di informazione asimmetrica gli acquirenti possono risultare vittime della cosiddetta 'maledizione del vincitore': se la loro offerta viene accettata sospetteranno che avrebbero potuto concludere un affare migliore. Può addirittura darsi il caso che qualsiasi offerta, se accettata, non avrebbe dovuto essere fatta. Si consideri una contrattazione tra due parti, riguardante un appezzamento di terreno in cui potrebbe esserci o non esserci un giacimento di petrolio. Entrambe le parti sanno che, mentre il proprietario del terreno conosce l'esatto valore che ha per lui il petrolio, l'acquirente potenziale sa solo che il valore, per il venditore, è una cifra compresa fra 0 e 100 milioni di dollari (tutti i valori all'interno di questo intervallo sono ugualmente probabili). Esse sanno anche che, quale che sia il valore del terreno per il venditore, per il potenziale acquirente esso vale il 50% in più, perché, per esempio, quest'ultimo possiede un terreno adiacente su cui potrebbe costruire una raffineria di petrolio. Si supponga ora che il compratore faccia un'offerta di X dollari, che il venditore accetta. Da ciò il compratore può desumere che il terreno valga, per il venditore, X dollari al massimo. Più precisamente, egli sa che, per il proprietario, il terreno vale una cifra compresa fra 0 e X dollari (tutti i valori all'interno di questo intervallo sono ugualmente probabili). Dal punto di vista dell'acquirente, quindi, il valore atteso del terreno, per il venditore, è X/2, mentre per lui è del 50% in più, cioè 3X/4. Ma questa cifra è inferiore a quella che egli si è offerto di pagare. Rendendosi conto che qualsiasi offerta egli faccia, se fosse accettata, gli procurerebbe un appezzamento di terreno che vale meno di quanto l'abbia pagato, l'acquirente deciderà di non fare alcuna offerta. Benché vi sia l'opportunità di concludere un affare vantaggioso per entrambe le parti, non se ne farà nulla.Quando le informazioni non sono complete, vi è il rischio che accordi pur vantaggiosi per tutte le parti in causa non si realizzino. Per risolvere il problema le parti contraenti possono sforzarsi di essere sincere. In generale non esiste un modo per convincere l'altra parte che si sta dicendo la verità. In questi casi può rivelarsi utile una reputazione di onestà e sincerità. Per acquisire tale reputazione occorre agire onestamente e sinceramente in situazioni in cui non è vantaggioso farlo. Pertanto il fatto di agire contro i propri interessi può avere una giustificazione razionale. Analogamente alcuni possono decidere, razionalmente, di crearsi la reputazione di persone irrazionalmente vendicative. Gli altri, non meno razionalmente, penseranno che vi sia una certa probabilità che i primi siano realmente irrazionali e una certa probabilità che stiano solo fingendo.
Scelte collettive
Organizzazioni e gruppi devono spesso prendere decisioni vincolanti per tutti i membri. Sorge quindi il problema della razionalità collettiva: come può il gruppo prendere una decisione che sia in un certo senso ottimale? L'utilitarismo classico rispondeva a questa domanda affermando che si dovrebbe agire in modo da massimizzare la somma delle utilità di tutti i membri. Ciò presuppone che si possano confrontare i livelli di utilità di individui diversi. Né la funzione di utilità ordinale (v. cap. 2), né quella di utilità cardinale (v. cap. 4) consentono confronti del genere, dato l'ampio grado di arbitrarietà che le caratterizza. Alcuni studiosi sostengono che non ha senso confrontare utilità di individui diversi. Un'opinione più diffusa è quella secondo cui questi confronti non hanno alcuna rilevanza sul piano pratico, in quanto nessuno ha ancora ideato una procedura operativa che consenta di effettuarli. Oggi si tende a ricondurre le decisioni collettive alle preferenze ordinali, procedendo nel modo appresso specificato. Dato un certo numero di alternative, si supponga che ogni singolo agente possegga un insieme completo e coerente di preferenze nei confronti di tali alternative. Si vuole individuare una procedura che consenta di riunire queste preferenze individuali in un 'insieme ordinato di preferenze sociali' anch'esso completo e coerente. La procedura in questione deve soddisfare le seguenti condizioni. La condizione del dominio universale: la funzione usata deve assegnare un ordine di preferenza sociale a ogni insieme di preferenze individuali. In altre parole, non è permesso assumere che l'interesse personale escluda la presenza di ordini di preferenza 'perversi' né che la cultura corrente escluda un'eccessiva diversità di preferenze. La condizione dell'ottimo paretiano: se tutti i membri di una società preferiscono un'alternativa a un'altra, anche la società deve ordinare le alternative in questo modo. La condizione di non dittatura: le preferenze della società non devono coincidere sempre con quelle di un particolare individuo, prescindendo dalle preferenze degli altri. La condizione di indipendenza dalle alternative irrilevanti: l'ordine di preferenza sociale tra due alternative deve dipendere soltanto dall'ordine in cui esse sono preferite dagli individui. Per esempio, l'ordine di preferenza sociale tra x e y non deve cambiare solo perché alcuni individui che prima preferivano y a z ora preferiscono z a y.
Kenneth Arrow ha dimostrato, nel 1950, che non è possibile soddisfare tutte queste condizioni simultaneamente. In forma più rudimentale il problema era conosciuto da tempo. Alla fine del XVIII secolo il marchese di Condorcet scoprì il problema delle maggioranze cicliche, che si può illustrare con l'esempio seguente. Si consideri un'assemblea municipale che debba scegliere tra costruire una piscina coperta, sovvenzionare l'orchestra sinfonica locale e costruire un campo da golf. Si supponga che nell'assemblea vi siano tre blocchi, più o meno delle stesse dimensioni, che rappresentano gli uomini d'affari, gli operai e i liberi professionisti. Si supponga anche che questi gruppi ordinino le proprie scelte, secondo il rispettivo stereotipo, nel modo seguente:
Uomini d'affari Operai Liberi professionisti
Campo da golf 1 2 3
Orchestra 2 3 1
Piscina 3 1 2
Una maggioranza, composta dagli uomini d'affari e dagli operai, pensa sia meglio avere un campo da golf che sovvenzionare l'orchestra; un'altra maggioranza, formata dagli uomini d'affari e dai liberi professionisti, ritiene sia meglio sovvenzionare l'orchestra che costruire una piscina; una terza maggioranza, costituita dagli operai e dai liberi professionisti, preferisce la piscina al campo da golf. La scelta della maggioranza è circolare, ovvero incoerente. Ciò che Arrow ha dimostrato è che non esiste un metodo ottimale per effettuare scelte collettive, se si accettano le condizioni del suo teorema. Fatta eccezione per la condizione di non dittatura, tutte le altre sono state messe in discussione, soprattutto quella dell'ottimo paretiano e quella dell'indipendenza dalle alternative irrilevanti. Nessuna di queste obiezioni, tuttavia, ha trovato un consenso unanime. A quarant'anni dalla sua prima formulazione, il 'teorema di impossibilità' di Arrow appare assai solido.
Studi comportamentali del processo decisionale
Sono state fatte numerose scoperte empiriche circa il modo in cui gli individui, in pratica, prendono le decisioni nella vita di tutti i giorni e nell'ambito dell'attività professionale. In questo capitolo esamineremo alcune deviazioni dal modello normativo tratteggiato nei capitoli 2 e 4. Il modello di comportamento basato sull'utilità attesa non sembra confermato dalla pratica effettiva, per tre motivi fondame
ntali. In primo luogo, poiché gli individui ignorano i principî basilari dell'inferenza statistica o causale, essi si formano opinioni erronee a partire dall'osservazione diretta. In secondo luogo, dati i propri obiettivi e le proprie stime di probabilità relative ai diversi risultati possibili, gli individui non riescono a massimizzare l'utilità attesa. In terzo luogo, gli individui si dimostrano sensibili a differenze nel modo in cui vengono loro presentate le varie possibilità, differenze che, invece, dovrebbero essere considerate irrilevanti.Ecco alcuni esempi di deduzioni scorrette. Durante la seconda guerra mondiale i londinesi erano persuasi che i tedeschi concentrassero sistematicamente i bombardamenti su determinati punti della città, poiché le bombe cadevano a grappoli. Questa deduzione tradisce l'ignoranza del principio statistico secondo cui i processi casuali tendono a generare raggruppamenti. Se le bombe tedesche fossero cadute uniformemente su tutta la città, allora sì che sarebbe stato pienamente giustificato il sospetto di una distribuzione non casuale. Gli istruttori dell'aviazione israeliana hanno notato che, quando i piloti vengono puniti dopo una cattiva prestazione, le loro prestazioni successive sono migliori, mentre, quando vengono premiati per una buona prestazione, le loro prestazioni successive non sono migliori. Da questa osservazione hanno tratto la conclusione che le punizioni sono più efficaci delle ricompense, una conclusione che tradisce l'ignoranza del principio statistico della regressione verso la media.
Nella Democrazia in America Tocqueville ha discusso la seguente obiezione alla democrazia. Quando, eccezionalmente, accade che i giovani francesi seguano l'usanza democratica di sposarsi per amore, anziché accettare un'unione combinata dai genitori, i loro matrimoni tendono a essere infelici. Da ciò si potrebbe dedurre che nei sistemi democratici esistono più matrimoni infelici che in altri regimi. Tocqueville sostiene che questa deduzione è sbagliata, perché non si può operare una generalizzazione sulla base di ciò che succede 'ai margini'. Nelle società dove i matrimoni per amore rappresentano l'eccezione, questi generano un'ostilità, che, a sua volta, crea risentimento fra i coniugi. Inoltre il fatto di andare contro corrente presuppone un carattere caparbio e ostinato che non contribuisce certo alla felicità del matrimonio.Il fatto che gli individui a volte non riescano a massimizzare l'utilità attesa può essere evidenziato confrontando le risposte fornite ai seguenti problemi decisionali.
Problema 1. Che cosa preferisci: una vincita certa di 30 $; (A) oppure la possibilità di vincere 45 $; con l'80% di probabilità (B)?
Problema 2. Che cosa preferisci: la possibilità di vincere 30 $; con il 25% di probabilità (C) oppure la possibilità di vincere 45 $; con il 20% di probabilità (D)?Negli esperimenti la maggior parte dei soggetti preferisce A nel problema 1 e D nel problema 2: un comportamento in contraddizione con l'ipotesi che i soggetti massimizzino l'utilità attesa. Supponiamo, infatti, che l'utilità attesa di 30 $; sia a e quella di 45 $; sia b. Preferire A nel problema 1 significa, allora, che a > 0,8b; preferire D nel problema 2, d'altro canto, significa che 0,25a 〈 0,2b, ovvero che a 〈 0,8b. La contraddizione è stata spiegata facendola risalire a un 'effetto certezza': la stessa identica riduzione della probabilità di un risultato ha un maggior impatto quando il risultato è inizialmente certo che quando è soltanto probabile. Sono stati osservati molti altri fenomeni dello stesso tipo, ma non si è raggiunto un accordo unanime su come spiegarli.Il fatto che differenze irrilevanti nel modo in cui vengono presentate le possibilità di scelta possano influenzare le decisioni è dimostrato dall'atteggiamento di chi utilizza la carta di credito. Le persone sono più riluttanti a usarla nei negozi che 'richiedono' un sovrapprezzo nel caso di pagamento con la carta di credito che non in quelli che 'promettono' uno sconto nel caso di pagamento in contanti, benché le due cose siano logicamente equivalenti. Più in generale, gli individui tendono a valutare le alternative in base a quanto queste differiscono da un punto di riferimento dato, piuttosto che in base agli stati finali. Mutamenti del punto di riferimento possono determinare cambiamenti delle preferenze. Così, in uno studio che sfruttava la discrepanza tra le valutazioni di grandi e piccoli guadagni, ai soggetti veniva data la possibilità di scegliere tra due calendari di ferie: il primo prevedeva 37 giorni di vacanza per due anni consecutivi, il secondo 44 giorni di vacanza nel primo anno e 30 nel secondo. In una condizione sperimentale i 30 giorni comuni a tutti i periodi di ferie erano tenuti separati dagli altri (30 + 7, 30 + 14, 30 + 0), nell'altra no (37, 44, 30). Le scelte effettuate nelle due situazioni sperimentali risultarono alquanto diverse: l'alternativa che offriva benefici immediati più consistenti fu preferita in maggior misura nella situazione in cui i 30 giorni comuni a tutti i periodi di ferie erano tenuti separati dagli altri. Lo studio dei comportamenti economici e la psicologia sperimentale hanno scoperto un numero crescente di anomalie di questo tipo, ma non è ancora chiaro quanta importanza esse abbiano nelle situazioni della vita reale. I fautori della teoria dell'utilità attesa sostengono che, quando si ha la possibilità di imparare dall'esperienza e la posta in gioco è più alta che nella maggior parte delle situazioni sperimentali, le incoerenze vengono rapidamente eliminate. Questa convinzione sembra contraddetta dal fatto che la linea di condotta adottata dagli istruttori dell'aviazione israeliana è largamente seguita e piuttosto persistente; ma ciò può dipendere dal fatto che non esiste un mercato perfetto degli istruttori di volo. (V. anche Azione sociale; Giochi, teoria dei; Razionalità).
Bibliografia
Ainslie, G., Picoeconomics, Cambridge 1990.
Arkes, H.R., Hammond, K.R. (a cura di), Judgement and decision making, Cambridge 1986.
Arrow, K., Social choice and individual values, New York 1963² (tr. it.: Scelte sociali e valori individuali, Milano 1977).
Diamond, P., Rotschild, M., Uncertainty in economics, New York 1978.
Elster, J., Ulysses and the Sirens, Cambridge 1979 (tr. it.: Ulisse e le sirene. Indagini sulla razionalità e l'irrazionalità, Bologna 1983).
Elster, J., Sour grapes, Cambridge 1983.
Elster, J. (a cura di), Rational choice, Oxford 1986.
Elster, J., Solomonic judgements, Cambridge 1989.
Elster, J., Hylland, A. (a cura di), Foundations of social choice theory, Cambridge 1986.
Friedman, J.W., Game theory with applications to economics, Oxford 1986.
Kahneman, D., Slovic, P., Tversky, A. (a cura di), Judgement under uncertainty: heuristics and biases, Cambridge 1982.
Keeney, R.L., Raiffa, H., Decisions with multiple objectives, New York 1976.
Kelly, J., Arrow impossibility theorems, New York 1978.
Loewenstein, G., Frames of mind in intertemporal choice, in "Management science", 1988, XXXIV.
Luce, R.D., Raiffa, H., Games and decisions, New York 1957.
Nisbett, R., Ross, L., Human inference: strategies and shortcomings of social judgement, Englewood Cliffs, N.J., 1980.
Raiffa, H., Decision analysis, Reading, Mass., 1968.
Rasmussen, E., Games and information, Oxford 1989.
Roth, A. (a cura di), Game-theoretic models of bargaining, Cambridge 1985.
Sen, A., Collective choice and social welfare, San Francisco 1970.
Tversky, A., Kahneman, D., The framing of decisions and the psychology of choice, in Rational choice (a cura di J. Elster), Oxford 1986.
Varian, H., Microeconomic analysis, New York 1984².