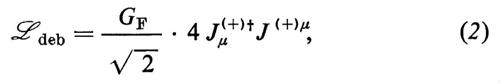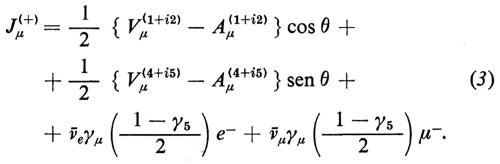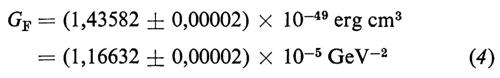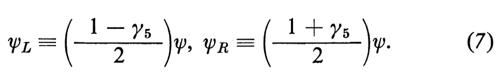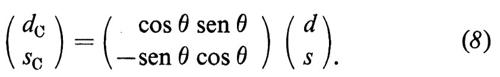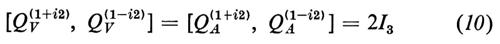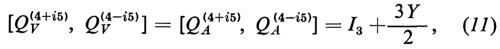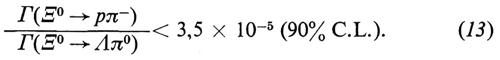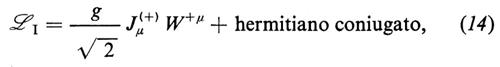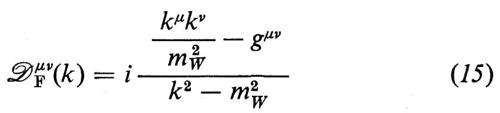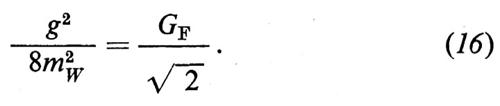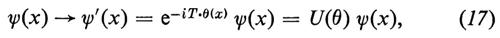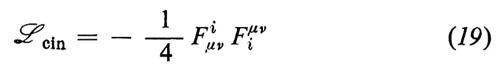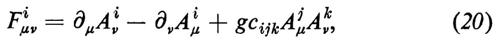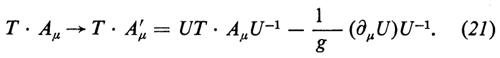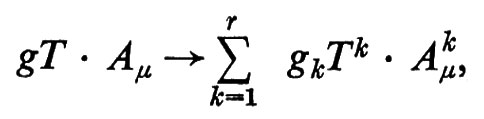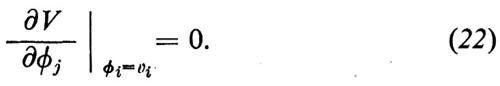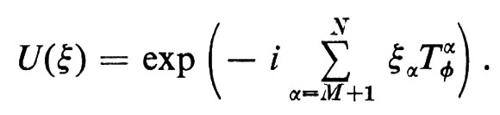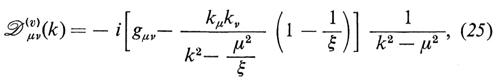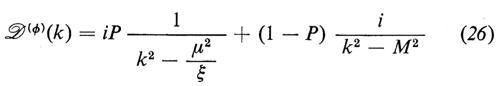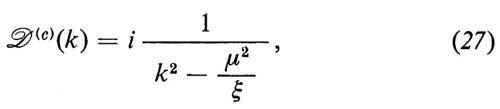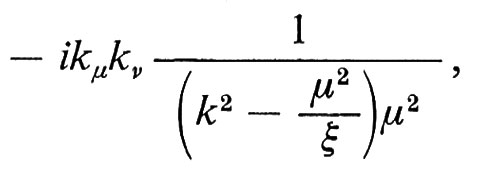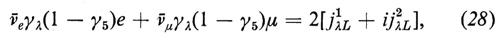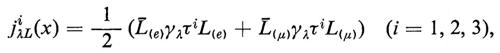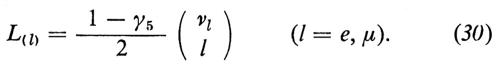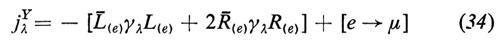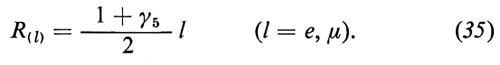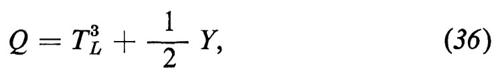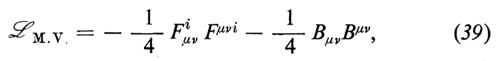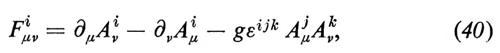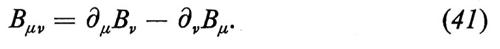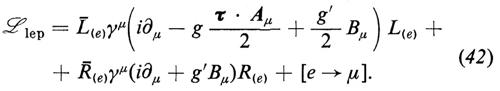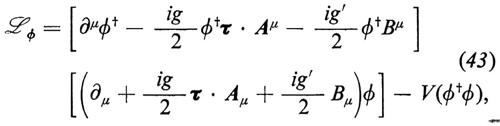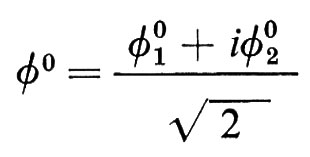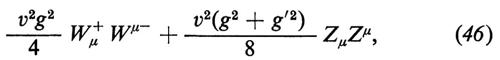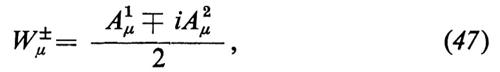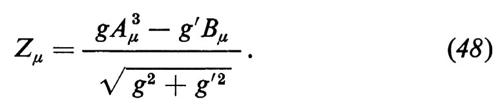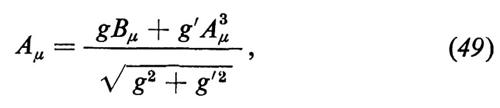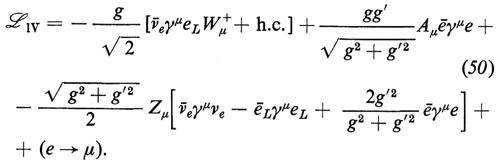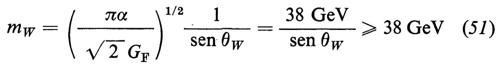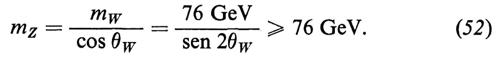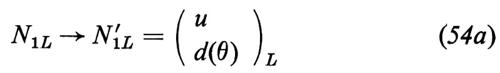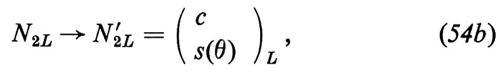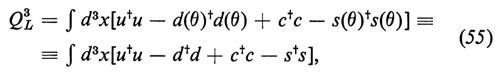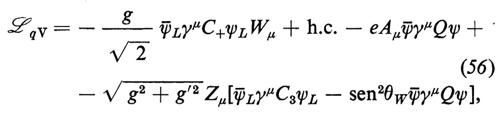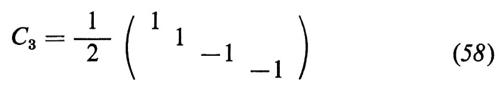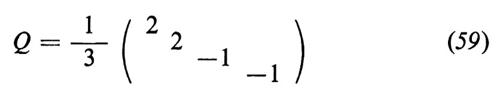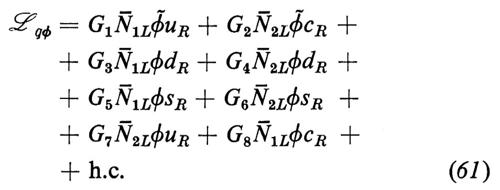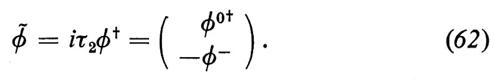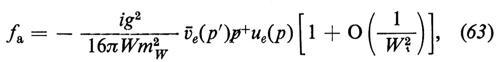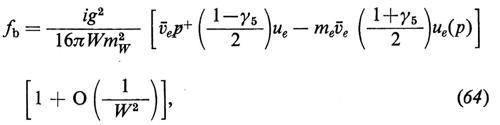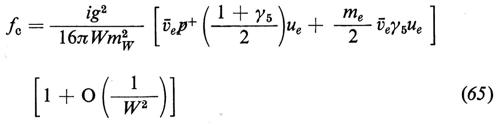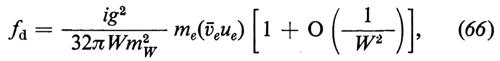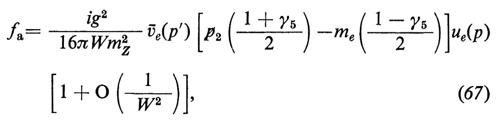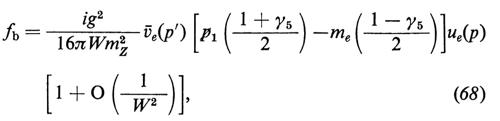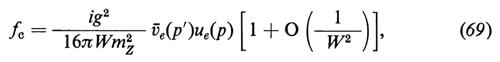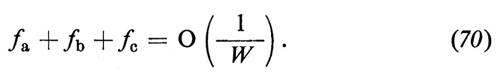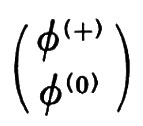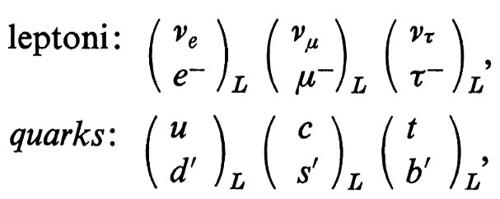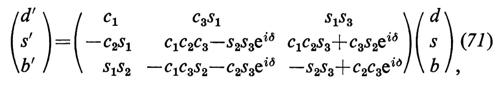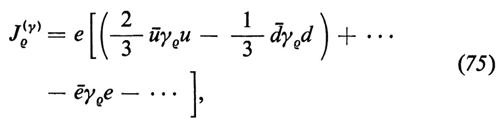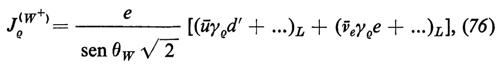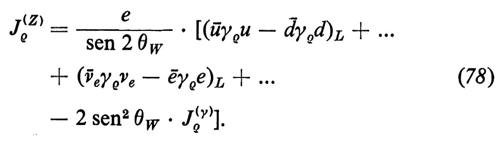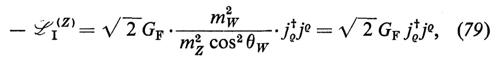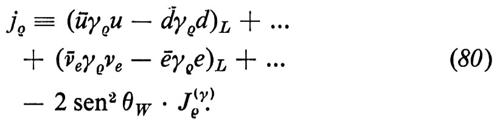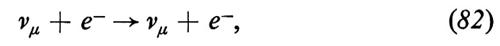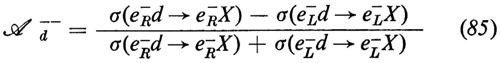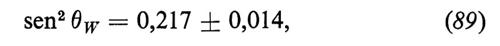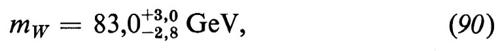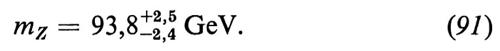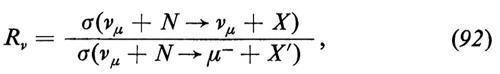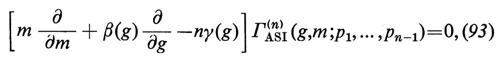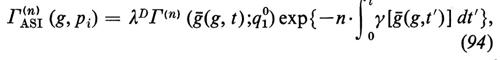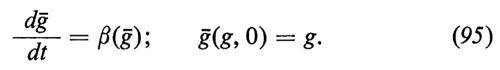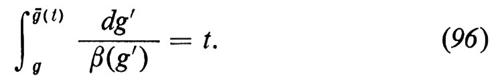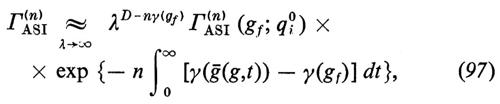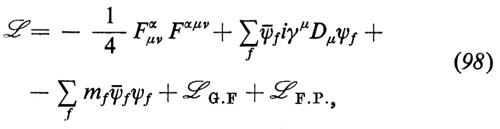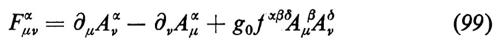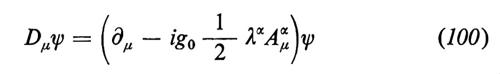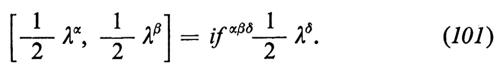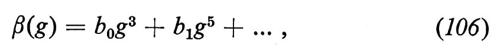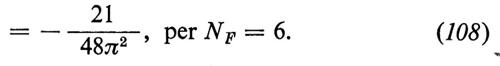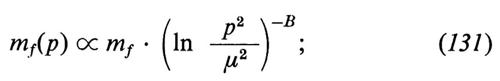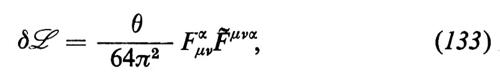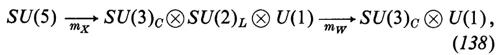Teorie unificate

Teorie unificate

di Mirza A. B. Bég

SOMMARIO: 1. Introduzione. □ 2. La sintesi elettrodebole: dinamica quantistica dei sapori: a) osservazioni preliminari; b) le interazioni deboli prima dell'introduzione delle teorie di gauge; c) teorie di gauge delle interazioni deboli; d) il modello di Salam e Weinberg. □ 3. Libertà asintotica. □ 4. Teoria di gauge delle interazioni forti: cromodinamica quantistica: a) caratteristiche generali; b) QCD perturbativa e fenomeni alle piccole distanze nella dinamica adronica; c) prospettive della QCD non perturbativa. □ 5. Il modello standard delle interazioni tra quarks e leptoni. □ 6. Grande unificazione e sintesi SU(5). □ 7. Critica della metodologia. □ 8. Problemi irrisolti; prospettive. □ Bibliografia.

1. Introduzione.

La nostra concezione dei fenomeni subnucleari ha subito una notevole evoluzione nel corso degli ultimi anni: oggi viene riconosciuto da tutti che la teoria dei campi di gauge (v. simmetrie e invarianze e particelle elementari: Struttura delle particelle) fornisce la descrizione più semplice ed elegante di tutte le interazioni tra particelle elementari. L'elettrodinamica quantistica (QED) - che, tra le teorie di gauge, è quella che ha conseguito i maggiori successi ed è anche la più semplice, in quanto si basa sul gruppo U(1) - non è più una disciplina a sé stante, ma è divenuta parte integrante della dinamica quantistica dei ‛sapori' (QFD), che abbraccia sia le interazioni elettromagnetiche che quelle deboli. Le interazioni forti, che, in un passato non tanto remoto, servirono da punto di partenza per alcuni tentativi di aggirare del tutto la teoria dei campi, vengono ora descritte dalla teoria di gauge che va sotto il nome di cromodinamica quantistica (QCD).

I fattori essenziali, che hanno condotto a quella che si potrebbe chiamare la ‛rivoluzione teorica di gauge' nella comprensione e nell'interpretazione dei processi delle particelle, sono stati i requisiti teorici di rinormalizzabilità per le interazioni deboli (v. Weinberg, 1967; v. Salam, 1968) e di libertà asintotica per le interazioni forti (v. Politzer, 1973; v. Gross e Wilczek, Ultraviolet behavior..., 1973). Divenne presto chiaro che i due problemi di descrivere le interazioni deboli in una maniera rinormalizzabile e di unificarle con le interazioni elettromagnetiche potevano essere affrontati contemporaneamente; in effetti, il principale vantaggio derivante da tale sintesi, ossia la scoperta che le interazioni deboli devono la loro debolezza alla massa elevata dei campi medianti (v. particelle elementari: Campi e particelle), continua ancor oggi ad avere una profonda influenza sul pensiero di molti fisici. Poiché ciò che sappiamo sulla struttura delle interazioni deboli alle basse energie implica che il gruppo di gauge debole deve contenere SU(2)_L, la scelta standard del gruppo elettrodebole unificante (v. Glashow, 1961; v. Salam e Ward, 1964; v. Weinberg, 1967), cioè SU(2)_L ⊗ U(1) (v. gruppi), è la più semplice tra quelle compatibili con le osservazioni. La storia della scoperta di tale gruppo costituisce da sola un argomento affascinante; in questa sede dovremo limitarci a ricordare che i primi incerti passi effettuati in quella che ora sappiamo essere la giusta direzione furono compiuti verso la fine degli anni trenta di questo secolo da O. Klein (1938) in un lungimirante studio che anticipò il lavoro fondamentale di Yang e Mills (v., 1954) e le sue applicazioni alla teoria elettrodebole.

Per giustificare la scelta del gruppo di gauge delle interazioni forti si deve ritornare all'epoca di SU(6) (v. Gürsey e Radicati, 1964); ci limiteremo qui soltanto a ricordare al lettore che questo gruppo permise di mettere ordine nello spettro dei barioni più leggeri (v. Gürsey e Radicati, 1964; v. Bég e Singh, 1964) e portò a importanti risultati sui momenti magnetici barionici (v. Bég e altri, 1964). Tutti questi risultati si basano sull'ipotesi che la funzione d'onda dei tre quarks in un barione sia completamente simmetrica sotto la permutazione dei gradi di libertà conosciuti; ma perché i risultati siano in accordo con il teorema spin-statistica è necessario che vi sia un nuovo grado tricotomico di libertà (v. Greenberg, 1964), che parecchi autori chiamano ‛colore'. I quarks di qualsiasi ‛sapore' risultano perciò triplicati e la lagrangiana assume un'ulteriore invarianza globale sotto un gruppo SU(3)_C. Trasformare questa invarianza globale in invarianza locale rappresenta il modo più naturale di introdurre le interazioni forti in modo che siano asintoticamente libere: la teoria che in precedenza abbiamo chiamato QCD è concepita appunto in tale maniera. La caratteristica più importante della QCD è che - a parte alcune precisazioni che faremo in seguito - essa presenta tutte le simmetrie conosciute delle interazioni forti. Pertanto le interazioni forti, quelle elettromagnetiche e quelle deboli di tutte le particelle elementari che si conoscono, almeno nella regione delle basse energie, possono essere derivate da un principio di gauge basato sul gruppo

G_B.E. = SU(3)_C ⊗ SU(2)_L ⊗ U(1). (1)

Sotto la spinta della sintesi elettromagnetica-debole sono state avanzate parecchie proposte interessanti per un'ulteriore sintesi, ossia l'inclusione di QCD e di QFD in una teoria di gauge basata su un gruppo di Lie di rango ≥ 4 convenientemente scelto. La soluzione più semplice del problema dell'unificazione è data dal gruppo SU(5) (v. Georgi e Glashow, 1974), che è un gruppo semplice, il quale fornisce quindi una descrizione a un solo parametro di tutte le interazioni di gauge: in particolare, l'angolo dell'interazione debole legato ai nomi di Glashow, Salam e Weinberg - un parametro caratteristico della teoria elettrodebole - è determinato dalla teoria e ha un valore compatibile con le osservazioni. Questo importante risultato della ‛grande unificazione' - con tale espressione viene spesso indicata la sintesi tra QFD e QCD - ha aperto la strada a indagini dettagliate sulle sue implicazioni, sia in campo teorico, sia in campo sperimentale; una gran parte delle ricerche è stata rivolta al calcolo e alla misura di un numero che in questa teoria si rivela essere finito, ossia la vita media del protone (a rigor di termini, il numero barionico non viene conservato neppure nel modello standard: v. ‛t Hooft, Symmetry breaking..., 1976; tuttavia, senza la grande unificazione, i tassi delle reazioni permesse risultano troppo bassi per poter essere osservati).

Nel presente articolo, basato in gran parte su alcuni miei lavori pubblicati a partire dal 1974 (v. Bég e Sirlin, 1974; v. i contributi di Bég, 1980; v. Bég, 1981; v. Bég e Sirlin, 1982), descriverò gli aspetti salienti degli sviluppi - che possono essere considerati importanti e duraturi - avutisi nella ricerca di una descrizione unificata delle forze della natura; prenderò in esame soltanto quelle teorie che soddisfano la condizione di essere rinormalizzabili a tutti gli ordini dello sviluppo perturbativo, sebbene tale criterio impedisca purtroppo di descrivere il più promettente fra i tentativi finora fatti per introdurre nella teoria anche la gravità, ossia la supersimmetria locale o supergravità (v., per es., Friedman, 1978). In questa interessantissima teoria, che ha in sé la possibilità di operare una sintesi tra le quattro forze fondamentali - ossia le forze forti, quelle deboli, l'elettromagnetismo e la gravità -, il dubbio sulla rinormalizzabilità sorge già al livello dei grafici di Feynman con tre circuiti chiusi di linee interne (‛anelli'): fintanto che tale problema resterà irrisolto e non si individuerà un altro modo di includere la gravità (v. Adler, 1982; v. Zee, 1981) rimarrà aperta la ricerca di una vera unificazione.

2. La sintesi elettrodebole: dinamica quantistica dei sapori.

a) Osservazioni preliminari.

Questa sintesi, nella sua forma moderna, ebbe origine dai contributi fondamentali di Weinberg (v., 1967) e di Salam (v., 1968). Entrambi questi autori ripresero la vecchia teoria secondo la quale le interazioni deboli e l'elettromagnetismo hanno una comune origine in un principio di gauge non abeliano, ma essi si discostarono dalla concezione tradizionale, suggerendo che la simmetria di gauge si rompa spontaneamente per effetto del meccanismo di Higgs e Kibble (v. i contributi di Higgs, 1964; v. Kibble, 1967), lasciando sopravvivere soltanto l'invarianza di gauge elettromagnetica. La speranza era che il meccanismo di Higgs avrebbe permesso a tale teoria di ritenere una memoria sufficiente del gruppo di gauge da rimanere rinormalizzabile - in contrasto con la situazione in cui la simmetria viene rotta inserendo esplicitamente un termine di massa nella lagrangiana: i lavori di ‛t Hooft (v. i contributi del 1971) e di Lee (v., 1972; v. Lee e Zinn-Justin, 1972 e 1973) dimostrarono che tale speranza era fondata.

Una volta superati gli ostacoli puramente teorici, l'attenzione si spostò verso il problema di trovare un modello in grado di riprodurre la realtà fisica; dopo vari falsi allarmi, si giunse a un modello del tutto adeguato, basato sul gruppo U(1) ⊗ SU(2)_L, proposto in origine per il settore leptonico da Weinberg (v., 1967) e completato da un procedimento proposto da Glashow, Iliopoulos e Maiani (v., 1970) per incorporare i quarks.

Mentre la metodologia teorica che sta alla base della sintesi elettrodebole è stata da molti criticata (torneremo in seguito su questo punto), la sua realizzazione basata sul gruppo U(1) ⊗ SU(2)_L, che va sotto il nome di QFD standard, ha avuto un notevole successo nella descrizione della struttura delle interazioni deboli: in effetti, le correnti deboli neutre, di cui, fino al 1973, veniva detto che ‟brillavano per la loro assenza" (v. Bég, 1963), furono scoperte sperimentalmente (v. Bég e Sirlin, 1982) dopo che questo modello ne aveva messo in evidenza l'importanza. Al momento attuale non si conoscono delle discrepanze tra la teoria e i risultati sperimentali.

b) Le interazioni deboli prima dell'introduzione delle teorie di gauge.

Per chiarire l'importanza della simmetria di gauge nella teoria delle interazioni deboli e al tempo stesso per introdurre gli elementi necessari per illustrare in maniera approfondita gli sviluppi più recenti, sarà necessario sintetizzare brevemente il punto a cui erano arrivate alla fine degli anni sessanta - ossia prima dell'introduzione delle moderne teorie di gauge - le ricerche sulle interazioni deboli. D'ora in poi considereremo che tutta la materia sia composta di leptoni (ν_e, e^-; ν_μ, μ^-; [ν_τ, τ^-]) e di quarks (u, d; [c], s; [t, b]): le parentesi quadre racchiudono le particelle che sono state scoperte solo nel corso degli anni settanta. Le proprietà che ci interessano dei quarks più leggeri sono il fatto che (u, d) costituiscono un isodoppietto dotato di ipercarica (forte) uguale a + 1/3, mentre s è un isosingoletto con ipercarica − 2/3.

1. L'interazione universale di Fermi. - Tutte le interazioni deboli fra correnti cariche sono adeguatamente descritte, alle basse energie, dalla lagrangiana fenomenologica corrente × corrente (v. Bég e Sirlin, 1974)

con

Gli indici in alto accanto a V e ad A - rispettivamente le correnti vettoriali e assiali adroniche - sono gli indici di SU(3) nella notazione abituale. I valori numerici attuali della costante di Fermi, G_F, e dell'angolo di Cabibbo, θ, sono rispettivamente (v. Bég e Sirlin, 1982):

e

cos θ = 0,973 ± 0,002. (5)

La corrente debole prende una forma assai semplice se la si esprime per mezzo dei campi dei quarks:

Jμ⁽⁺⁾ = (ūγ_μ d_C + ν̄_eγ_μe^- + ν̄_μγ_μμ^-)_L, (6)

dove il suffisso L posto dopo la parentesi indica che si prende la proiezione chirale levogira, ψ_L, di tutti i campi:

Inoltre, d_C è il campo ruotato alla Cabibbo:

Le equazioni (5) e (6) mostrano l'universalità originale tra le interazioni deboli dei quarks e dei leptoni; la connessione tra questa universalità originale e l'universalità fisica, che si riflette, per esempio, nella quasi uguaglianza delle costanti di accoppiamento nei decadimenti β e μ, è stabilita dalla CVC (v. Feynman e Gell-Mann, 1958; v. Gerstein e Zeldovich, 1956), dall'algebra delle correnti (v. Gell-Mann, 1962) e dalla PCAC (v. Bernstein e altri, 1960; v. Kuang-Chao Chou, 1961; l'interpretazione moderna nasce dagli studi di Wilson: v., 1969).

Secondo l'ipotesi della CVC, V_m⁽¹⁺ⁱ²⁾ rappresenta la corrente di isospin che aumenta la carica e appartiene allo stesso multipletto isotopico della parte isovettoriale della corrente elettromagnetica. Nella misura in cui l'isospin è un buon numero quantico, tale ipotesi assicura l'universalità degli accoppiamenti vettoriali che conservano la stranezza, con i valori nudi delle costanti di accoppiamento. Una conseguenza importante della CVC è che essa fornisce una previsione precisa dell'ampiezza delle transizioni magnetiche deboli isovettoriali (v. Gell-Mann, 1958); l'ipotesi della CVC è stata verificata con un elevato grado di precisione mediante lo studio sistematico delle transizioni nucleari (v. Wu, 1964; alcune questioni teoriche relative a questo argomento sono discusse in Bég e altri, 1972).

Di portata maggiore della CVC è invece la formulazione dell'universalità mediante l'algebra delle correnti. Definiamo le due cariche

QV^a = ∫ V0^a d³x; QA^a = ∫ A0^a d³x (9)

e consideriamo i commutatori a tempi uguali suggeriti dal modello a quark:

dove I₃ è la componente 3 dell'isospin e Y è l'ipercarica.

È chiaro che l'universalità leptone-adrone è esatta nel limite in cui gli elementi di matrice fra stati a una particella di questi commutatori sono saturati da stati intermedi a una sola particella. Per la corrente vettoriale ΔS = 0, questa saturazione con stati a una particella è una conseguenza dell'ipotesi CVC, che identifica Qa_V(a = 1, 2, 3) con i generatori dell'isospin; per la corrente vettoriale ∣ ΔS ∣ = 1, il teorema di Behrends, Sirlin, Ademollo e Gatto (v. Behrends e Sirlin, 1960; v. Ademollo e Gatto, 1964) ci assicura che il contributo degli stati intermedi a molte particelle è del secondo ordine nella rottura di SU(3). I commutatori assiali non possono venire saturati da stati con una sola particella neppure nel limite in cui le cariche sono conservate, poiché la conservazione di tali cariche è legata a una simmetria spontaneamente rotta, o simmetria di Nambu e Goldstone; per le cariche assiali, le valutazioni dei contributi a molte particelle, effettuate, per il caso ΔS = 0, da Adler (v., 1965) e Weisberger (v., 1965) usando la PCAC, concordano perfettamente con i risultati sperimentali.

Si osservi come, in questa descrizione convenzionale delle interazioni deboli, le correnti neutre (ossia quelle con ΔQ = 0) brillino per la loro assenza. I migliori limiti sperimentali si hanno per le correnti ΔQ = 0 e ∣ ΔS ∣ = 1 e derivano dal processo K0_L → μ⁺μ^-: il valore attuale del tasso di decadimento (v. Carithers e altri, 1973)

Γ(K_L → μ⁺μ^-) = 1,1 × 10^-8 Γ(K_L → tutto) (12)

è in accordo con l'ipotesi che il processo proceda interamente attraverso la sequenza K0_L → 2γ → μ⁺μ^-. A questo proposito sarà bene notare che l'assenza quasi assoluta del K0_L → μ⁺μ^- non può venire attribuita alla cancellazione tra le ampiezze ΔS = + 1 e ΔS = − 1: la presenza contemporanea di correnti con entrambi i segni di ΔS darebbe infatti origine ad ampiezze ∣ ΔS ∣ = 2 all'ordine più basso e ciò porterebbe a una differenza di massa K_L − K_S tanto grande da essere inaccettabile e inoltre non rispetterebbe i limiti imposti dal decadimento (Stech, 1973)

Infine notiamo che nel contesto dell'equazione (2) la regola ΔI = 1/2 per le transizioni non leptoniche e la sua generalizzazione a SU(3), ossia la dominanza dell'ottetto, devono essere considerate come altrettanti effetti dinamici.

2. Difficoltà della teoria di Fermi. - Il modello delle interazioni deboli che abbiamo appena delineato è soddisfacente soltanto a un livello superficiale: infatti basta sondare la teoria un poco più in profondità, utilizzando la lagrangiana ℒ_deb dell'equazione (2) per calcolare qualsiasi altra grandezza oltre alle ampiezze alle basse energie (per riprodurre le quali era stata ideata), per incorrere in serie difficoltà.

Si consideri in primo luogo il problema delle correzioni radiative (elettromagnetiche) (v. Bég e Sirlin, 1982; v. Wu, 1964; v. Bég e altri, 1972): è indispensabile calcolare tali correzioni poiché gli effetti all'ordine G_Fα rientrano nell'ambito della misurabilità. Nel settore leptonico si scopre che le correzioni al decadimento del μ sono finite a tutti gli ordini in α, ma le correzioni al processo ν_e + e^- → ν_e + e^- divergono all'ordine α² (v. Adler, 1969; v. Bell e Jackiw, 1969). Nel settore semileptonico si scopre che, se si trascurano gli effetti delle interazioni forti, le correzioni al decadimento n → p + e^- + ν̄_e divergono già all'ordine α; la speranza che le interazioni forti potessero ridurre tale divergenza fu completamente annullata dal lavoro di Dicus e collaboratori (v. Wu, 1964; v. Bég e altri, 1972); invero il teorema di Dicus, che è una conseguenza dell'algebra delle correnti, asserisce che le correzioni radiative all'ordine α alle transizioni semileptoniche ΔS = 0 indotte dalla corrente vettoriale sono infinite, seppure in una maniera universale (l'ampiezza, cioè, è ancora determinata dagli elementi di matrice di QV⁽¹⁺ⁱ²⁾; in tal caso l'universalità del tipo leptone-adrone, naturalmente, si perde). I tentativi di cancellare tale divergenza con la divergenza che deriva dal contributo della corrente assiale sono falliti, poiché è difficile garantire l'indipendenza di quest'ultima divergenza dalla dinamica delle interazioni forti. In presenza del campo elettromagnetico, perciò, non si può dire che la fenomenologia delle interazioni deboli sia una conseguenza delle equazioni (2) e (3).

Si consideri ora l'estrapolazione dell'equazione (2) alle alte energie. Come si sa, le ampiezze per le reazioni ν_μ + e^- → μ^- + ν_e e ν_e + e^- → ν_e + e^-, nella teoria di Fermi, superano i loro limiti unitari rispettivamente intorno a 300 GeV e a 450 GeV. (Questi processi nella teoria di Fermi sono puramente in onda S, e il rapporto tra la sezione d'urto prevista e il limite unitario aumenta come la quarta potenza dell'energia nel centro di massa!). Se si cerca di evitare questa ‛catastrofe unitaria' considerando la ℒ_deb data dall'equazione (2) come un'interazione di una teoria di campo capace di fornire una matrice S unitaria quando si vada oltre l'approssimazione di Born, si incorre in difficoltà ancora maggiori; infatti, tutti gli effetti di ℒ_deb agli ordini superiori sono infiniti in una maniera non rinormalizzabile e si finisce per perdere il controllo anche sulla fenomenologia alle basse energie.

La situazione, come si vede, è insostenibile: le difficoltà nascono, naturalmente, dal cattivo comportamento di ℒ_deb alle alte energie, comportamento che è responsabile della sua non rinormalizzabilità (nel significato convenzionale).

Gli infiniti di cui ci stiamo occupando furono notati per la prima volta da Heisenberg nel 1936, nel quadro della allora vigente teoria del decadimento β ed essi lo portarono a introdurre la nozione di ‛lunghezza fondamentale' nel 1938 (v. Heisenberg, 1936 e 1938).

3. Teoria del bosone vettoriale intermedio (IVB). - In questa formulazione, si parte dall'interazione di Yukawa

dove W⁺ è l'operatore del campo dei bosoni vettoriali carichi positivamente e J_μ⁽⁺⁾ è la corrente dell'equazione (3). Dalla forma covariante del propagatore del W

risulta chiaramente che, se ci si limita alle transizioni in cui il trasferimento di impulso e le masse delle particelle che partecipano sono piccole in confronto a m_W, gli effetti del secondo ordine in ℒ_I nell'equazione (14) si possono simulare mediante la lagrangiana ℒ_deb dell'equazione (2), purché si faccia la seguente identificazione:

Ciò che abbiamo detto della fenomenologia alle basse energie nel contesto della teoria di Fermi si applica anche, con le dovute sostituzioni, alla teoria del bosone intermedio, o teoria di Yukawa: il comportamento dell'interazione di Yukawa alle alte energie è, naturalmente, molto diverso da quello dell'interazione di Fermi, ma purtroppo, in questo contesto, non è affatto più favorevole.

4. Dfficoltà della teoria dell'IVB. - Le difficoltà che incontra la teoria dell'IVB sono differenti, nei dettagli, da quelle incontrate dalla teoria di Fermi; tuttavia, il tipo dei problemi rimane sostanzialmente invariato.

Nel campo delle correzioni radiative elettromagnetiche si scopre che, nella maggior parte dei processi, le correzioni divergono a tutti gli ordini in α. In alcuni casi di particolare interesse, quale il calcolo delle correzioni di ordine α al rapporto G_V/G_μ (per quanto riguarda gli studi meno recenti, v. Bég e Sirlin, 1974), si è dimostrato (nelle teorie in cui il W non ha momento magnetico anomalo) che anche in presenza di interazioni forti le divergenze si cancellano nel risultato finale, purché si trascurino i termini di ordine αq²/m²_W (dove q è l'impulso trasferito); i termini di quell'ordine sono, tuttavia, divergenti. In altri casi, quale il rapporto tra i tassi dei decadimenti del μ e del W, le difficoltà della divergenza si presentano all'ordine α anziché a quello m²_μ/m²_W: queste sono delle chiare manifestazioni della non rinormalizzabilità della teoria. Se i mesoni W hanno un fattore giromagnetico g = 2, le divergenze nelle correzioni fotoniche di ordine α al decadimento del μ, per esempio, si possono assorbire in una ridefinizione delle costanti di accoppiamento g_νeeW e g_νμμW, relative ai vertici ν_eeW e ν_μμW; tuttavia tali costanti diventano parametri liberi, indeterminati e non legati tra loro, cosicché va persa la possibilità di prevedere rapporti tra tassi di decadimento, quali Γ(W → μ + ν̄_μ)/Γ(W → e + ν̄_e) o Γ(μ → e + ν̄_e + ν_μ)/Γ(W → e + ν̄_e). Allo stesso modo si sa che per g = 2 le correzioni fotoniche di ordine a al momento magnetico anomalo del μ sono finite. Tuttavia, poiché la teoria non è rinormalizzabile, sembra assai improbabile che questi risultati limitati continuino a valere agli ordini più alti della teoria delle perturbazioni.

Lo scoglio dell'unitarietà, all'ordine g², non sembra insormontabile, se ci si limita a processi quali ν_μ + e^- → μ^- + ν_e oppure ν_e + e^- → ν_e + e^-: le ampiezze d'onda parziali in questi processi (che non sono dei puri processi di onda S nella teoria IVB) violano i loro limiti unitari soltanto in maniera logaritmica con l'energia. Questo superamento logaritmico dei limiti unitari, nell'approssimazione di Born, si verifica in teorie rispettabilissime come l'elettrodinamica quantistica (QED); tuttavia, nella QED sappiamo come generare una matrice S unitaria, includendo effetti di ordine più alto, mentre in questo caso non siamo in grado di fare altrettanto. Ad ogni modo la contraddizione più spettacolare con l'unitarietà, con sezioni d'urto che violano i limiti unitari secondo una potenza dell'energia, come avviene nella teoria di Fermi, si presenta anche nella teoria IVB, se si esaminano altri processi accuratamente scelti: per esempio, nel processo ν_μ + ν̄_μ → W⁺ + W^- l'ampiezza di elicità (− 1/2, 1/2) → (0, 0) supera il limite unitario a ~ 10³ GeV (v. Low, 1968; v. Gell-Mann e altri, 1969).

Come avviene per la teoria di Fermi, le difficoltà della teoria IVB nascono dal cattivo comportamento di quest'ultima alle alte energie, comportamento che, a sua volta, è responsabile dell'impossibilità di rinormalizzare la teoria stessa. Tuttavia, al contrario di quanto succedeva per la teoria di Fermi, esiste in questo caso una possibilità di risolvere tale difficoltà. Il colpevole, nella teoria IVB, può essere identificato nel termine k_μk_ν del propagatore del W; se si trovasse un modo per tenere sotto controllo tale termine, si potrebbe sperare di ottenere una teoria ragionevole delle interazioni deboli.

Ricordiamo a questo punto che un esempio di teoria nella quale il termine incriminato del propagatore vettoriale non provoca alcun problema è costituito dall'elettrodinamica con un termine di massa. In questa teoria, tuttavia, non soltanto il mesone vettoriale si accoppia a una corrente conservata, ma si ha inoltre l'arbitrarietà latente della scelta della gauge; tale arbitrarietà può essere utilizzata per quantizzare la teoria stessa in una gauge nella quale essa è chiaramente rinormalizzabile (v. Zimmerman, 1969).

5. Tentativi per ottenere delle risposte finite. - Sono stati fatti molti tentativi per ottenere delle risposte finite da teorie non rinormalizzabili. Alcuni di essi si basavano sulla speranza che le difficoltà di tali teorie nascessero da un uso ingiustificato della teoria delle perturbazioni e che tali difficoltà si sarebbero risolte se ci si fosse potuti liberare del contesto perturbativo. Il fondamento di una tale speranza risiede nella teoria dei sistemi a molti corpi, ma purtroppo, nonostante si siano fatti parecchi coraggiosi tentativi in questa direzione (v. Bég e Sirlin, 1974), nessuno è per ora riuscito a dimostrare che tale filosofia può essere applicata anche alla teoria delle interazioni deboli.

L'inattuabilità dei metodi non perturbativi ha portato a una rinascita di interesse per quella che si può chiamare la ‛teoria fenomenologica delle perturbazioni' (v. Bég e Sirlin, 1974; v. Low, 1968; v. Gell-Mann e altri, 1969). In questa si utilizza l'interazione debole dell'equazione (2) e della (14) per generare uno sviluppo formale perturbativo: tutti gli integrali divergenti vengono tagliati a una certa massa Λ considerata come un parametro libero da determinarsi sperimentalmente. Gli effetti degli ordini più alti sono normalmente proporzionali a G_F Σ_n {a_n(G_FΛ²)ⁿ + altri termini meno singolari}; perché essi non disturbino la struttura fenomenologica espressa dal termine di Born è indispensabile scegliere un valore piuttosto basso di Λ(≈ 10 GeV). È assai difficile comprendere quali siano le origini di un valore così basso; inoltre, esso può dar luogo a imbarazzanti paradossi, dato che le energie attualmente usate negli esperimenti possono facilmente scandagliare la regione in cui si trova Λ.

Il tentativo più recente di salvare le interazioni deboli senza introdurre un metodo radicalmente nuovo è stato effettuato da Gell-Mann e collaboratori (v. Low, 1968; v. Gell-Mann e altri, 1969): essi hanno cercato di cancellare (alle alte energie) il termine k_μk_ν nel propagatore del W introducendo dei campi scalari con accoppiamenti derivativi. Per i campi fisici, in contrapposizione ai ‛fantasmi', il segno del propagatore scalare è tale che si può verificare una cancellazione soltanto se l'accoppiamento del campo scalare a uno dei vertici è opposto a quello all'altro vertice. È chiaro che questa strategia è inapplicabile ai processi diagonali del tipo di ν_e + e^- → ν_e + e^-, ma si può invece sperare che funzioni per i processi non diagonali, del tipo di ν_μ + e^- → μ^- + ν_e. Nonostante l'accoppiamento tra i processi diagonali e quelli non diagonali, la tattica della cancellazione funziona, comunque, per una gran parte dei processi non diagonali, nella misura in cui le divergenze che si verificano agli ordini più alti sono esclusivamente logaritmiche; le ampiezze diagonali che hanno un alto grado di divergenza devono essere definite con prescrizioni arbitrarie che, fortunatamente, possono essere riassorbite nelle definizioni delle masse, delle costanti di accoppiamento e di altri parametri. Per trattare le divergenze rimanenti bisogna tagliare gli integrali all'energia alla quale i grafici di Born superano il limite unitario [~ O(10³ GeV)]. Sebbene questo metodo sia più soddisfacente dei tentativi fatti per preservare le regole di selezione dei termini dominanti mediante un taglio a Λ ≈ 10 GeV, è chiaro che esso non può che essere provvisorio, in attesa che veda la luce una teoria più valida.

Perché una teoria possa essere presa seriamente in considerazione dobbiamo assicurarci in qualche modo che essa non sia soltanto l'affermazione di un pensiero astratto; in particolare, essa dovrà permettere di eseguire dei calcoli e dovrà fornire un certo numero di previsioni verificabili sperimentalmente. Le limitazioni imposte dallo stato attuale della teoria ci obbligano, perciò, a rimanere, almeno per ora, entro il campo delle teorie rinormalizzabili. Inoltre, supponiamo che la forma ‛corrente × corrente' dell'interazione non sia un aspetto casuale e che le correnti V − A abbiano un ruolo naturale nella teoria: in altre parole, respingiamo le alternative ‛a inganno' (per alcuni esempi delle quali v. Low, 1968; v. Gell-Mann e altri, 1969). La scelta si restringe, perciò, alle teorie di gauge, ed è appunto di queste che ci accingiamo a trattare.

c) Teorie di gauge delle interazioni deboli.

1. Caratteristiche generali. - La formulazione delle teorie rinormalizzabili che unificano le interazioni deboli e quelle elettromagnetiche si basa su una combinazione di alcune idee teoriche assai sottili e di teoremi molto eleganti. La prima idea è la richiesta che la teoria rimanga invariata sotto l'azione di trasformazioni locali di gauge; ciò introduce in maniera naturale i mesoni vettoriali che saranno alla fine identificati con il fotone e con i bosoni intermedi delle interazioni deboli. Il problema fondamentale di costruire delle teorie invarianti sotto un gruppo locale di gauge G fu risolto da Yang e Mills (v., 1954); qui ne diamo un breve riassunto.

I campi ψ della teoria si trasformano secondo

dove

sono le matrici che rappresentano gli N generatori di G e θⁱ(x) sono i parametri della trasformazione locale. La lagrangiana invariante per trasformazioni di gauge viene allora costruita per mezzo delle sostituzioni

∂_μ ψ(x) → D_μ ψ(x) = (∂_μ − igT • A_μ) ψ(x) (18)

e introducendo un termine che contenga le parti cinetiche e le autointerazioni dei mesoni vettoriali:

dove c_ijk sono le costanti di struttura di G. (Si usa la convenzione che gli indici ripetuti vanno sommati: quelli greci da 0 a 3, quelli latini da 1 a N).

L'invarianza della lagrangiana e garantita se i campi vettoriali obbediscono alla legge di trasformazione inomogenea

Si noti che si devono introdurre N mesoni vettoriali, uno per ogni generatore di G, e si osservi che termini di massa espliciti per gli A_μ romperebbero l'invarianza di gauge, per cui gli A_μ sono privi di massa.

Tali condizioni sono valide se G è un gruppo di Lie semplice. Se G è il prodotto diretto di gruppi semplici, G = G₁ ⊗ G₂ ... ⊗ G_r, si sostituisce

dove T^k sono i generatori di G_k. Perciò, in questa teoria, appaiono r costanti indipendenti di accoppiamento, una per ciascun gruppo G_k. L'equazione (18) illustra una delle motivazioni originali più importanti per usare la teoria di Yang e Mills come base per unificare le interazioni deboli e quelle elettromagnetiche. Si consideri, per esempio, il caso in cui il gruppo G sia semplice: nella teoria appare allora soltanto una costante di accoppiamento g. In tal caso, si può identificare g con la carica dell'elettrone − e e inoltre le cariche elettriche delle varie particelle non possono essere arbitrarie, ma devono anzi essere quantizzate in unità di e. La costante di accoppiamento debole è anch'essa legata a e in una maniera assai semplice, che dipende dal contenuto in rappresentazioni della teoria; in altre parole, si raggiunge così la soluzione del problema annoso di introdurre il concetto di universalità in una maniera elegante e convincente. Come vedremo in seguito, in molti modelli G possiede un sottogruppo invariante U(1), per cui le cariche elettriche rimangono in quei casi arbitrarie. Tuttavia, il sogno dell'universalità rimane ancora in parte realizzato, poiché molte delle costanti fenomenologiche di accoppiamento risultano collegate tra loro, o addirittura identiche le une alle altre.

Un importante sviluppo teorico, relativamente recente, nello studio delle teorie di Yang e Mills è costituito dalla derivazione di un insieme autoconsistente di regole di Feynman (v. Abers e Lee, 1973; v. Bég e Sirlin, 1982; v. Faddeev e Popov, 1967); in questo contesto si è rilevato molto vantaggioso il metodo di quantizzazione basato sugli integrali sulle storie. Da queste ricerche è emerso che le regole di Feynman per le teorie non abeliane di gauge non sono date direttamente dai vertici della lagrangiana originale; per trovarle bisogna anche tener conto di vertici e di propagatori supplementari associati a campi scalari fittizi che obbediscono alla statistica di Fermi: chiameremo questi campi ‛fantasmi scalari fermionici'.

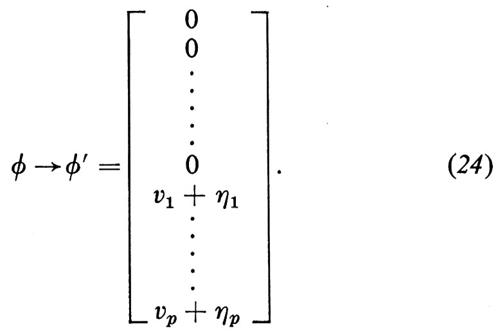
Sebbene una teoria delle interazioni deboli basata su un principio di gauge esatto sia rinormalizzabile, il fatto che i campi di gauge del tipo di W^± siano privi di massa impedisce che essa possa descrivere la realtà fisica; occorre introdurre delle masse per tutti i campi di gauge, tranne che per quello del fotone, in modo tale però che la teoria mantenga una memoria sufficiente dell'invarianza e rimanga rinormalizzabile. La seconda idea importante, che porta poi alla risoluzione del problema, è la rottura spontanea della simmetria: lo stato di vuoto, ossia lo stato fondamentale, non è invariante sotto la simmetria completa della lagrangiana. Per ottenere questo risultato si introduce una serie di campi scalari hermitiani ϕ che si trasformano secondo una rappresentazione di G a n dimensioni. I campi ϕ introducono nella lagrangiana un termine V(ϕ) di energia potenziale che è un polinomio quartico (quartico per non distruggere la rinormalizzabilità della teoria), i cui valori minimi si ottengono per valori dati dei campi scalari ϕ_i = v_i:

Se alcuni dei v_i sono diversi da zero, si ha 〈0 ∣ ϕ_i ∣ 0> ≠ 0 e la simmetria si rompe spontaneamente. In particolare, alcuni dei generatori del gruppo non lasciano invariante il vuoto; le matrici rappresentative corrispondenti, Tϕ^α, nello spazio degli indici dei ϕ sono caratterizzate da (Tϕ^α)_ijv_j ≠ 0. I generatori che lasciano invariante il vuoto soddisfano invece le condizioni (Tϕ^α)_ijv_j = 0 (α = 1, 2,..., M) e formano un sottogruppo S di G: S è perciò il gruppo di simmetria della teoria fisica. Nelle teorie convenzionali senza mesoni vettoriali, il teorema di Goldstone assicura che, per ogni generatore conservato T^α(α = M + 1, M + 2, ..., N) di G, che rompe la simmetria del vuoto, ci deve essere nella teoria una particella di massa nulla e spin 0, con gli stessi numeri quantici della simmetria interna, che caratterizzano i T^α. Del teorema di Goldstone esistono molte dimostrazioni, che sono talmente note da non dover essere ripetute in questa sede (v. Goldstone e altri, 1962); ci basti qui ricordare che tutte queste dimostrazioni si basano sia sulla positività della metrica nello spazio di Hilbert, sia sulla covarianza manifesta o sulla località.

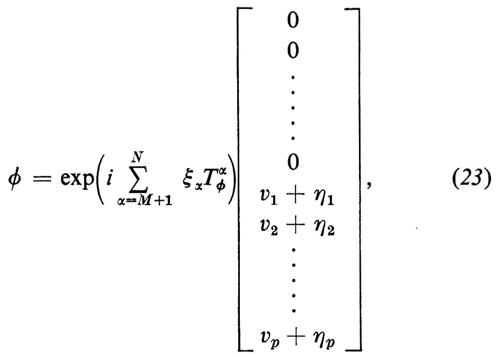
Nel caso delle teorie di gauge rotte spontaneamente, le due difficoltà, cioè l'assenza di massa dei quanti di gauge e la presenza di indesiderati bosoni di Goldstone, si neutralizzano a vicenda in virtù del fenomeno di Higgs e Kibble (v. i contributi di Higgs, 1964; v. Kibble, 1967). Infatti, mediante una trasformazione del gruppo di gauge locale, effettuata sulla lagrangiana, gli scalari privi di massa possono venir eliminati dalla teoria e essere assorbiti nei campi trasformati dei mesoni vettoriali, che acquistano così una massa. Ciò si ottiene cambiando anzitutto le variabili di campo per mezzo di una sostituzione non lineare dovuta a Higgs e Kibble:

dove la sommatoria in α è fatta su N − M generatori di G che rompono la simmetria del vuoto, i campi ‛, sono bosoni di Goldstone potenziali e i campi η_i [i = 1, 2, ..., p = n − (N − M)] completano i rimanenti gradi di libertà scalari. A questo punto, gli ξ_α si possono rimuovere mediante la trasformazione di gauge rappresentata dalle equazioni (15) e (21) con la scelta specifica

Invero, per effetto di questa trasformazione si ottiene

Quelli che avrebbero dovuto essere i bosoni di Goldstone, cioè gli ξ_α, sono stati eliminati dalla lagrangiana: essi sono stati, infatti, assorbiti nei campi A′_μ secondo la legge di trasformazione (21).

I mesoni vettoriali A′_μ accoppiati ai generatori T^α(α = M + 1, ..., N), che rompono la simmetria del vuoto, sono degli oggetti massicci. Ciò è facile da capire dal punto di vista fisico, poiché gli A′_μ così ridefiniti hanno acquistato un ulteriore grado di libertà associato ai bosoni di Goldstone eliminati e i campi vettoriali con tre gradi di libertà di elicità sono necessariamente dei campi massicci. Invece i mesoni vettoriali accoppiati ai generatori che lasciano invariato il vuoto rimangono privi di massa. Di solito, nella costruzione dei modelli, si dispongono le cose in maniera tale che il gruppo di simmetria S della teoria fisica sia U(1); il mesone vettoriale corrispondente rimane privo di massa e si identifica con il fotone, mentre gli altri mesoni vettoriali diventano massicci e si identificano con i bosoni intermedi delle interazioni deboli. Gli η_i sono gli scalari di Higgs: particelle fisiche che rimangono nella lagrangiana e svolgono un ruolo importante nell'assicurare l'unitarietà e la rinormalizzabilità. La trasformazione speciale U(ξ) equivale alla scelta di una particolare gauge, la cosiddetta gauge unitaria, caratterizzata dall'assenza di bosoni di Goldstone nella densità lagrangiana.

La rinormalizzabilità della teoria originale di Yang e Mills, senza massa, si mantiene nonostante la rottura spontanea della simmetria! Soltanto recentemente si è potuta trovare una dimostrazione di questo fatto singolare (v. i contributi di t'Hooft, 1971; v. Lee, 1972; v. Lee e Zinn-Justin, 1972 e 1973); il modo più semplice di provarlo fa uso delle cosiddette gauge rinormalizzabili, in cui nella densità lagrangiana sono presenti dei campi corrispondenti a eccitazioni non fisiche. In queste gauge i propagatori dei mesoni vettoriali, i mesoni scalari e i fantasmi scalari fermionici hanno rispettivamente le forme (v. Abers e Lee, 1973)

e

dove μ² e M² sono i quadrati delle matrici di massa dei mesoni vettoriali e degli scalari di Higgs, P è un operatore di proiezione sul sottospazio a N − M dimensioni sotteso dai bosoni di Goldstone e ξ è un parametro che specifica la particolare gauge scelta.

Le funzioni di Green di questa teoria dipendono da ξ, ma gli elementi della matrice S sono indipendenti dal parametro di gauge, come si può dimostrare con il metodo della quantizzazione mediante gli integrali sulle storie (v. Abers e Lee, 1973; v. Bég e Sirlin, 1982; v. Faddeev e Popov, 1967); quest'ultima proprietà è la conseguenza matematica dell'invarianza di gauge della teoria.

Se poniamo ξ ≠ 0, tutti i propagatori si comportano come 1/k², per k → ∞; questa situazione è simile a quella dell'elettrodinamica quantistica. I metodi usuali di teoria delle perturbazioni che si basano sul conteggio delle potenze dimostrano che la teoria è rinormalizzabile e perciò le gauge con ξ ≠ 0 vengono dette ‛gauge rinormalizzabili'. Per studiare la rinormalizzazione ed effettuare dei calcoli pratici è molto utile disporre di un procedimento gauge-invariante di regolarizzazione, come avviene nel caso dell'elettrodinamica quantistica. Il procedimento di Pauli e Villars che si usa nella QED non può essere esteso al caso non abeliano: in questo caso il procedimento più conveniente è invece la regolarizzazione dimensionale introdotta da ‛t Hooft e Veltman (v., 1972).

Nelle gauge rinormalizzabili vi sono dei contributi alle funzioni di Green dovuti ad alcune particelle non fisiche. Abbiamo già indicato che i D^(c)(k) sono i propagatori dei fantasmi scalari fittizi di ‛statistica sbagliata'; aggiungiamo ora che il secondo termine in D(μ%νv )% e il primo termine in D^(ϕ) presentano dei poli a k² = μ²/ξ, che non possono corrispondere allo spettro fisico, poiché - per non dire che una ragione - essi dipendono dal parametro di gauge; aggiungiamo, inoltre, che il secondo termine in D(μ%νv )% differisce dal solito propagatore di un mesone vettoriale massiccio per un termine

che corrisponde formalmente al contributo di scalari di metrica negativa il cui gradiente è accoppiato alla sorgente dei mesoni vettoriali. Il legame di alcune di queste eccitazioni non fisiche con i bosoni di Ooldstone si rivela chiaramente se si prende ξ = ∞, ossia una gauge con poli a k² = 0. In D^(ϕ) i poli a k² = 0 corrispondono chiaramente ai bos6ni di Goldstone fittizi.

Se invece si prende ξ = 0, i poli non fisici scompaiono da D^(ϕ) e D^(v) diventa il solito propagatore per un mesone vettoriale massiccio con tre elicità. In questa gauge la teoria è manifestamente unitaria, poiché i poli non fisici sono stati esplicitamente rimossi dalle funzioni di Green: vediamo perciò che la scelta di ξ = 0 corrisponde alla gauge unitaria. I fantasmi scalari fermionici lasciano una traccia nella gauge unitaria. Sebbene il loro propagatore si annulli per ξ → 0, alcuni dei loro vertici sono proporzionali a 1/ξ. Di conseguenza, in questo limite, il contributo dei fantasmi scalari può essere valutato in forma chiusa ed esso aggiunge un termine non polinomiale alla densità hamiltoniana della gauge unitaria. D'altra parte, in questa gauge, D(μ%νv )% (k) si comporta come O(1) per k → ∞ e la rinormalizzabilità non è più manifesta.

La strategia più semplice per trattare la rinormalizzabilità e l'unitarietà della teoria è quella di prendere ξ ≠ 0, per dimostrare la rinormalizzabilità, e prendere in seguito ξ = 0 per dimostrare l'unitarietà: poiché la matrice S è indipendente da ξ, si può in tal modo dimostrare sia la rinormalizzabilità che l'unitarietà della teoria stessa.

Per i modelli di gauge costruiti a partire da gruppi chirali di gauge, la rinormalizzabilità impone un'altra importante condizione. Generalmente in modelli di tale tipo possono verificarsi delle anomalie triangolari (v. Adler, 1969; v. Bég e Sirlin, 1982), la cui esistenza viola le identità formali di Ward della teoria, rompe l'indipendenza da ξ della matrice S e distrugge la rinormalizzabilità a ordini sufficientemente alti della teoria delle perturbazioni. Per garantire il successo del programma di rinormalizzazione, è dunque necessario costruire dei modelli in maniera tale che le anomalie triangolari si cancellino internamente; ciò non è difficile da realizzare, poiché i contributi all'anomalia sono indipendenti dalla massa dei fermioni effettivi negli anelli triangolari. Tuttavia questa condizione pone dei limiti notevoli al contenuto in rappresentazioni della teoria.

2. Metodologia. - La costruzione di teorie specifiche di gauge si basa sulle idee generali esposte fin qui. Il primo passo è la scelta del gruppo di gauge e l'assegnazione dei vari campi fondamentali della teoria alle singole rappresentazioni; tra questi campi c'è una serie di mesoni scalari che agiscono da ‛catalizzatori' di una rottura spontanea della simmetria. La densità lagrangiana viene poi costruita combinando questi multipletti in maniera gauge-invariante, secondo le regole discusse nel precedente punto 1. Illustreremo tale procedimento servendoci del modello di Salam e Weinberg, o modello di S-W (v. Weinberg, 1967; v. Salam, 1968), sperando che il lettore possa farsi un'idea della formulazione generale delle teorie di gauge e delle regole che si seguono per la costruzione di modelli diversi o più estesi (ma pur sempre canonici). Per l'esposizione di formulazioni non canoniche si rimanda il lettore ad alcune pubblicazioni citate in bibliografia (v. i contributi di Bég, 1980; v. Bég, 1981).

d) Il modello di Salam e Weinberg.

1. Formulazione a quattro sapori. - Questo modello, che ha quattro sapori leptonici e quattro sapori di quark, fu, in ordine di tempo, il primo tentativo di unificare le interazioni elettromagnetiche e quelle deboli dei quarks e dei leptoni nel quadro di una simmetria di gauge spontaneamente rotta; esso si basa sul gruppo di gauge SU(2)_L ⊗ U(1) (l'indice L indica che i generatori corrispondenti agiscono sui campi levogiri).

Per giustificare la costruzione di questo modello, ricordiamo che la corrente leptonica delle interazioni deboli si può scrivere nel modo seguente:

Chiameremo ji_λL(x) correnti di ‛isospin leptonico'; le cariche corrispondenti

Ti_L = ∫ ji_0L d³x (31)

chiudono l'algebra di SU(2)_L:

[Ti_L, Tj_L] = iε^ijkTk_L. (32)

La corrente elettromagnetica dei leptoni può essere scritta nel modo seguente:

dove si ha

e

In particolare, la carica elettrica Q è data da

dove

Y = ∫ j0^Y d³x. (37)

L'‛ipercarica leptonica' Y commuta con i generatori dell'isospin leptonico e perciò Ti_L e Y chiudono l'algebra di SU(2)_L ⊗ U(1). L'idea è di usare questo gruppo come simmetria di gauge del modello; per questo si introducono tre mesoni vettoriali, Ai_μ, legati a SU(2)_L, e uno, B_μ, legato a U(1). I multipletti levogiri, L_(l), vengono assegnati alla rappresentazione bidimensionale di SU(2)_L. Il legame esistente tra Q e Y mostra che L_(l) ha ipercarica Y = − 1. I leptoni destrogiri, R_(l), sono singoletti di SU(2)_L con ipercarica Y = − 2. Gli scalari di Higgs sono assegnati alla rappresentazione bidimensionale di SU(2)_L, con Y = 1; essi possono, perciò, essere raggruppati in un doppietto

formato da una componente carica positivamente e da una neutra.

Il secondo passo consiste nel combinare questi multipletti in maniera gauge-invariante, per costruire la densità lagrangiana. Ci dovrà essere un termine ℒ_M.V. che rappresenta le parti cinetiche e le autointerazioni dei mesoni vettoriali:

Il termine leptonico che dà origine all'interazione tra i leptoni e i mesoni vettoriali è

Il contributo scalare è dato da

dove

V(ϕ^✝ϕ) = μ²ϕ^✝ϕ + λ(ϕ^✝ϕ)².

Il parametro λ deve essere positivo affinché sia garantito che l'hamiltoniana sia limitata inferiormente. Se μ² > 0, il minimo dell'‛energia potenziale' V(ϕ), in una teoria classica, si ha per ϕ = 0; se, invece, μ² 〈 0, il minimo si ha per ∣ ϕ ∣ = v/√-2 = √-−-(-μ-²/-2-λ-) ≠ 0. Questo fatto ha un analogo nell'approssimazione ad albero della corrispondente teoria quantistica, ossia 〈0 ∣ ϕ ∣ 0> = v/√-2 ≠ 0. Nell'approssimazione ad albero tutti i diagrammi che comportano delle integrazioni sulle linee chiuse vengono trascurati. In tal caso 〈0 ∣ ϕ ∣ 0> è dato dal valore v che minimizza V(ϕ). Per studiare i valori di aspettazione nel vuoto all'ordine superiore, è consigliabile usare il metodo dei potenziali effettivi (v. Coleman e Weinberg, 1973). In questo caso la simmetria si rompe spontaneamente.

Ponendo

(dove ϕ0₁ e ϕ0₂ sono campi hermitiani) e servendosi dell'invarianza di gauge della lagrangiana, è sempre possibile scegliere 〈0 ∣ ϕ0₂ ∣ 0> = 0, 〈0 ∣ ϕ1⁺ ∣ 0> = 0 e 〈0 ∣ ϕ0₁ ∣ 0> = v. Inoltre, si può scegliere v reale. Tale scelta permette di vedere che i generatori Ti_L e Y rompono la simmetria del vuoto: soltanto la loro combinazione lineare corrispondente alla carica elettrica Q lascia invariante il vuoto.

Nel caso di gruppi chirali, si possono costruire termini di massa invarianti soltanto accoppiando singoletti destrogiri e levogiri. Nel modello di Salam e Weinberg, a causa della mancanza di singoletti levogiri, questo non è possibile. Per generare le masse elettroniche e muoniche in maniera gauge-invariante, si introduce un accoppiamento di Yukawa tra i leptoni e gli scalari:

ℒ_lϕ = − G_(e)Ò_(e)ϕ^✝L_(e) − G(μ)Ò(μ)ϕ^✝L(μ) + h.c. (44)

Per studiare il contenuto fisico della teoria, si effettua la seguente sostituzione:

ϕ0₁ = ϕ1⁰′ + v. (45)

È allora facile verificare che i campi ϕ0₂, ϕ⁺ e ϕ^-, nell'approssimazione ad albero, sono tutti di massa nulla, mentre il campo ϕ1⁰′ ha una massa il cui quadrato è − 2μ² > 0. ϕ0₂, ϕ⁺ e ϕ^- si possono dunque identificare con i bosoni di Goldstone fittizi della teoria e possono essere eliminati mediante una trasformazione di Higgs e Kibble. Secondo i teoremi generali di cui ci occuperemo nel capitolo finale del presente articolo, tre dei mesoni vettoriali diventano massicci dopo la rottura spontanea della simmetria, mentre il quarto mesone vettoriale rimane invece privo di massa. Gli autovettori della matrice di massa nella gauge unitaria si possono ottenere esaminando i termini bilineari nei campi dei mesoni vettoriali; inserendo l'equazione (45) nella (43) si vede subito che tali valori sono dati da

Perciò W+_μ e W−_μ si identificano con mesoni vettoriali carichi di massa m_W = gv/2, mentre il campo hermitiano Z_μ è un mesone vettoriale neutro di massa

mz = ‛'²v/2.

La combinazione ortogonale

che corrisponde a un autovalore nullo della matrice di massa, si identifica con il fotone.

In termini di questi campi fisici, l'interazione tra leptoni e mesoni vettoriali data dall'equazione (42) si può scrivere nella forma seguente:

Possiamo perciò identificare gg′/√-g-²--+-g-′² con e (− e è la carica dell'elettrone). Il legame esistente tra la costante di accoppiamento dei W^± e la costante fenomenologica universale G_F delle interazioni deboli è ancora dato dall'equazione (16). Introducendo l'angolo di Salam, Ward e Weinberg, θ_W = tan^-1 (g′/g), in modo che sia e = g sen θ_W, otteniamo

e

La teoria prevede, perciò, dei limiti inferiori molto grandi per m_Z ed m_W. La rottura spontanea della simmetria genera anche le masse di e e di μ attraverso gli accoppiamenti dell'equazione (44): si trovano perciò le relazioni m_e = G_(e)v/√-2 e m_μ = G_(μ)v/√-2.

È importante osservare che il modello SU(2)_L ⊗ U(1) con elettroni e muoni soltanto non è in realta rinormalizzabile, a causa dell'esistenza delle anomalie triangolari.

Finora abbiamo escluso dalla nostra analisi gli adroni; uno dei problemi fondamentali che si devono affrontare per incorporare gli adroni nella teoria è il fatto sperimentale che i decadimenti semileptonici con ΔS = 1 che richiedono correnti leptoniche neutre sono soppressi di parecchi ordini di grandezza (v. eq. 12).

Per assicurare l'assenza delle correnti con ΔQ = 0, ΔS = 1, si utilizza l'artificio proposto da Glashow, Iliopoulos e Maiani (GIM) (v. Glashow e altri, 1970); il modo più semplice per realizzare tale artificio consiste nell'introdurre due doppietti di SU(2)_L costruiti mediante quattro quarks:

Il quark c si distingue per un nuovo numero quantico, generalmente chiamato charm.

Finché i quarks hanno massa zero, i campi dotati di proprietà di trasformazione ben definite sotto isospin debole sono anche campi fisici (ossia campi caratterizzati da una massa definita); il meccanismo per generare la massa, che descriveremo nel seguito, può, tuttavia, provocare un mescolamento, cosicché i due gruppi di campi non sono più uguali. Si può dimostrare senza difficoltà che tutti gli effetti di mescolamento possono venir assorbiti nel settore d − s e perciò, dopo la diagonalizzazione della matrice di massa, i due doppietti fisici sono

e

dove d(θ) ed s(θ) sono i campi ruotati alla Cabibbo, che abbiamo introdotto nell'equazione (8).

Il generatore ΔQ = 0 di SU(2)_L si può scrivere nella maniera seguente:

che mostra che esso non contiene alcun termine con ΔS ≠ 0.

Ci si potrà domandare perché non vi sia un mescolamento dello stesso tipo nel settore leptonico, tra e^- e μ^-. La risposta a tale interrogativo è facile: il mescolamento può essere trasferito al settore ν_eν_μ ed eliminato con una rotazione, poiché si pensa che ν_e e ν_μ abbiano masse uguali tra loro e uguali a zero.

Le interazioni tra quarks e mesoni vettoriali si possono scrivere nella maniera seguente:

dove si ha

Si noti che Z ha soltanto accoppiamenti diagonali nel sapore al livello albero, come, d'altronde, ci si attendeva; tuttavia, agli ordini superiori, si presentano accoppiamenti del tipo di Z_μ ã γ^μs.

Le masse dei quarks sono generate nello stesso modo in cui si generano le masse leptoniche, ossia scrivendo prima di tutto l'accoppiamento di Yukawa più generale gauge-invariante:

Poi si isolano i termini di massa, ponendo ϕ = 〈0 ∣ ϕ ∣ 0> ed eseguendo una trasformazione unitaria sui campi fermionici, per diagonalizzare la matrice di massa; tale trasformazione porta al mescolamento alla Cabibbo cui ci riferivamo in precedenza.

Infine si noti che, con le solite assegnazioni di carica per i quarks (Q_u = Q_c = + 2/3, Q_d = Q_s = − 1/3), la cancellazione delle anomalie triangolari - che interferirebbero con la rinormalizzabilità della teoria - è automatica, se ogni quark si presenta in tre colori. Le anomalie derivanti dagli anelli leptonici si cancellano con quelle derivanti dagli anelli dei quarks, indipendentemente per ciascuna generazione; ovvero (ν_e, e^-, u, d) è una rappresentazione riducibile di U(1) ⊗ SU(2)_L senza anomalie, come pure (ν_μ, μ^-, c, s)..

2. Comportamento alle alte energie. - La non rinormalizzabilita della teoria convenzionale delle interazioni deboli è strettamente collegata al cattivo comportamento delle ampiezze alle alte energie. Per esempio, le divergenze quadratiche della fig. 1 sono legate alla crescita con l'energia dell'ampiezza della fig. 2A; ciò è facilmente spiegabile, poiché il contributo del canale s alla parte assorbitiva della fig. 1 è proporzionale alla sezione d'urto per il processo ν + ν̄ → W⁺ + W^-.

Questa osservazione porta a una conseguenza molto semplice: per avere una teoria rinormalizzabile delle interazioni deboli dobbiamo introdurre delle nuove particelle oltre ai soliti leptoni e mesoni W^±, per cancellare la crescita dell'ampiezza della fig. 2A; ci deve perciò essere o un mesone vettoriale neutro massiccio che contribuisce al canale s di ν + ν̄ → W⁺ + W^- (v. fig. 2B), oppure un leptone pesante che contribuisce al canale u (v. fig. 2C), o addirittura entrambi insieme.

Illustreremo ora come le teorie rinormalizzabili producano delle ampiezze di Born per quei processi fisici che non superano il limite unitario; come esempi ci serviremo delle ampiezze per e⁺ + e^- → W⁺ + W^- e e⁺ + e^- → 2Z nel modello di Salam e Weinberg nel caso in cui i due mesoni vettoriali massicci siano emessi in stati di elicità zero. Per semplificare i calcoli, abbiamo scelto g′ = g, ossia θ_W = π/4.

Vi sono quattro diagrammi, rappresentati nella fig. 3, che contribuiscono a e⁺ + e^- → W⁺ + W^- nell'approssimazione di Born. Un calcolo elementare dà, per il caso in cui W⁺ e W^- siano emessi in stati di elicità zero,

e

dove W è l'energia totale nel c.d.m., p⁺ è il quadrimpulso del W⁺ e gli f rappresentano (1/8πW) volte le ampiezze invarianti. Quando e^- ed e⁺ hanno elicità opposte, f_a e i primi termini in f_b ed f_c crescono linearmente con W, mentre f_d e i secondi termini di f_b ed f_c diminuiscono come 1/W. Se poniamo m_e = 0, le interazioni scalari e quelle pseudoscalari non possono produrre e^- ed e⁺ con elicità di segno opposto. Con m_e ~ 0, l'ampiezza di tale vertice è inibita da un fattore supplementare di soppressione pari a m_e/W. La crescita lineare di f_a con W è legata al fatto che nelle teorie di gauge i mesoni W hanno un momento magnetico anomalo di un magnetone di Bohr che corrisponde a un fattore giromagnetico g = 2. Inoltre, l'analisi della dipendenza angolare dei primi termini che contribuiscono a f_a, f_b ed f_c dimostra che i contributi vengono soltanto dall'ampiezza parziale con J = 1; in tale caso, il limite dell'unitarietà richiede che l'ampiezza per e^- + e⁺ → W⁺ + W^- diminuisca come 1/W. Le equazioni (63-65) dimostrano che sebbene ciascun diagramma cresca in maniera lineare con W, le interazioni deboli e quelle elettromagnetiche cooperano in maniera tale che f_a + f_b + f_c si comporta come 1/W per W grande, senza mai superare il limite dell'unitarietà. Se e^- ed e⁺ hanno la medesima elicità, si verifica la stessa cosa quando si combinano i quattro diagrammi, come dimostrano le equazioni (63-66); ciò spiega il ruolo importante svolto dallo scalare fisico di Higgs nel cancellare quei termini che si comportano come O(1) per W grande, termini che supererebbero altrimenti il limite dell'unitarietà.

L'esempio più semplice che illustra il ruolo che svolge lo scalare di Higgs è probabilmente il processo e^- + e⁺ → 2Z (v. fig. 4). Quando i due Z sono in stati di elicità zero, si ottengono le seguenti ampiezze per g = g′:

dove p₁ e p₂ sono i quadrimpulsi degli Z.

Un semplice calcolo mostra che

Troviamo di nuovo che il contributo dello scalare di Higgs è essenziale per cancellare i termini costanti quando e^- ed e⁺ hanno la stessa elicità.

In sintesi, il comportamento delle teorie di gauge spontaneamente rotte è, alle alte energie, abbastanza buono da portare alla rinormalizzabilità e da risolvere completamente i problemi dell'unitarietà della teoria convenzionale, che abbiamo illustrato nel È b. Il ragionamento si può capovolgere: imponendo il comportamento voluto per i grafici ad albero alle alte energie, si può derivare la struttura delle teorie di gauge spontaneamente rotte (v. Cornwall e altri, 1973).

3. Estensione a sei sapori. - Kobayashi e Maskawa (K-M) notarono (v. Kobayashi e Maskawa, 1973) che il modello di Salam e Weinberg con un campo fisico reale di Higgs e quattro sapori, ciascuno formato da leptoni e quarks, non poteva dar luogo alla violazione dell'invarianza CP - scoperta da Fitch e altri (v., 1964) nel 1964 - e non poteva perciò costituire una descrizione esauriente della realtà fisica. Per avere nella lagrangiana fasi non rimovibili che violino CP, si può far ricorso a diverse alternative; a) allargare il gruppo di gauge e accettare nella teoria dei nuovi campi di gauge (v., per es., Bég e Tsao, 1978); b) allargare il settore di Higgs (v., per es., Weinberg, 1976); c) aumentare il numero dei sapori dei fermioni in modo da avere almeno un'altra generazione di quarks e di leptoni; d) scegliere una combinazione di due o più delle suddette possibilità. Se il gruppo di gauge di S-W è considerato intoccabile e se si vuole una teoria in cui sia possibile la violazione di CP (e se, inoltre, non si vuole indagare più in profondità e domandarsi se CP sia rotta esplicitamente oppure spontaneamente), l'alternativa c) sembra la più elegante, se usata da sola - ed effettivamente la scelta di K-M cadde proprio su di essa. La conferma sperimentale venne dalla scoperta del leptone τ, da parte di Perì e altri (v., 1975; v. Perl, 1980), e della particella ipsilon, da parte di Lederman e altri (v., 1977); quest'ultima dimostra l'esistenza di un quinto quark.

L'insieme dei campi che occorre associare attualmente al modello di Salam e Weinberg può essere riassunto nella maniera seguente:

campi di gauge: W⁺, W^-, Z, γ,

(la parte hermitiana di ϕ⁽⁰⁾ sopravvive come campo fisico, mentre le altre parti sono assorbite nel meccanismo di Higgs),

quarks e leptoni destrogiri: tutti singoletti.

Gli apici su d, s e b indicano che i campi sono legati da una trasformazione unitaria ai campi di massa definita; più precisamente,

dove c_i = cos θ_i, s_i = sen θ_i (i = 1, 2 o 3) e δ è una fase che viola CP.

La matrice dell'equazione (71) è la generalizzazione a sei sapori della matrice di Cabibbo dell'equazione (8). Nel limite in cui la violazione di CP viene trascurata (δ = 0), si è determinato che i tre angoli del tipo di Cabibbo valgono (v. Bég e Sirlin, 1982)

dove X⁰ e Y⁰ denotano degli ‛errori grossi'. Per una valutazione di tali errori e per un'analisi delle difficoltà incontrate nel determinare θ₂ e θ₃ mediante i dati sperimentali, rimandiamo il lettore agli articoli citati in Bég e Sirlin (v., 1982).

4. Implicazioni sperimentali al livello albero. - Al livello senza anelli chiusi, o livello albero, il modello di S-W riproduce la fenomenologia consueta associata alle interazioni indotte da correnti cariche; inoltre, esso permette di fare delle previsioni sulle interazioni indotte da correnti neutre. Un'analisi sperimentale di quest'ultimo tipo di interazioni, iniziata nel 1973 (v. Hasert e altri, 1973), portò all'accettazione generale di questo modello.

Le quattro correnti del modello si possono scrivere nella forma

e

Qui Jρ^(y) è la corrente elettromagnetica, Jρ^(W±) sono le solite correnti cariche e Jρ^(Z) è la corrente neutra debole. Gli indici L in basso indicano, come al solito, la proiezione chirale levogira dei campi fermionici. I puntini indicano le generazioni più alte di quarks e di leptoni.

L'interazione mediata da Z si può scrivere, nel limite delle basse energie, nella maniera seguente:

dove

Per ottenere la seconda uguaglianza dell'equazione (79) ci siamo serviti del fatto che nel modello di S-W con solo doppietti di Higgs vale la relazione

m_Z cos θ_W = m_W (81)

(conosciuta anche sotto il nome di regola ΔI_deb = 1/2).

L'equazione (79) è ricca di contenuto e ha in sé un solo parametro libero, ossia sen² θ_W. Tra le quantità predette dalla teoria che sono già state misurate (v. Bég e Sirlin, 1974 e 1982) ricordiamo le seguenti.

a) Sezioni d'urto per i processi

(dove X sta per stati finali adronici).

b) Asimmetria nella diffusione anelastica profonda di elettroni polarizzati sul deuterio

(dove σ denota una sezione d'urto doppiamente differenziale).

c) Attività ottica del vapore di Bi atomico (ossia rotazione del piano di polarizzazione della luce laser che passa attraverso il vapore, dovuta agli effetti della violazione di parità nell'atomo di Bi).

d) Simmetria avanti-indietro nella reazione e⁺e^- → μ⁺μ^-. In ognuno di questi casi si ottiene un buon accordo tra teoria e osservazione per il valore

sen² θ_W ≈ 0,22, (86)

che corrisponde a

m_W ≈ 80 GeV, (87)

m_Z ≈ 90 GeV. (88)

Nella discussione delle correzioni radiative daremo gli errori legati a questi numeri.

5. Correzioni radiative a un anello. - Il fatto che le teorie di gauge spontaneamente rotte siano rinormalizzabili ha suscitato una rinascita di interesse per lo studio delle correzioni radiative elettromagnetiche e degli effetti deboli agli ordini più alti (v. Bég e Sirlin, 1974 e 1982). Tra le ricerche effettuate in tal senso citiamo: a) il riesame dei calcoli tradizionali; b) lo studio di nuovi problemi caratteristici delle teorie unificate delle interazioni deboli ed elettromagnetiche.

Due esempi del primo tipo di ricerche sono costituiti dagli studi delle correzioni radiative alle differenze di massa, all'universalità elettrone-muone, al decadimento dei muoni, al decadimento β e ad altri tipi di decadimenti semileptonici, e dai calcoli dei contributi deboli al momento magnetico anomalo del muone e alla diffusione fotone-fotone. Due esempi del secondo tipo di ricerche sono, invece, lo studio delle condizioni nelle quali è possibile dimostrare l'assenza di violazione di parità e di stranezza, all'ordine α, e il calcolo di processi proibiti agli ordini più bassi, come K_L → μ⁺ + μ^-.

Per illustrare alcuni concetti generali, soffermiamoci brevemente sulle correzioni all'ordine α al decadimento del μ. Poiché la teoria è rinormalizzabile, gli elementi di matrice del decadimento del μ devono essere finiti se espressi in termini delle costanti di accoppiamento rinormalizzate g_Weνe, g_Wμνμ e delle masse fisiche. La ragione di ciò è chiara: nelle teorie rinormalizzabili, i controtermini devono avere dimensioni canoniche ≤ 4; perciò qualsiasi divergenza residua nel decadimento del μ dopo la rinormalizzazione delle costanti di accoppiamento e delle masse violerebbe la rinormalizzabilità della teoria stessa, poiché per cancellarla sarebbe necessario un controtermine di dimensione canonica uguale a sei. Lo stesso ragionamento si può applicare al decadimento β e a qualsiasi ampiezza a quattro fermioni. Tuttavia, quando le teorie di gauge erano agli inizi, era importante e utile controllare la cancellazione di tali divergenze residue. Studi ulteriori condussero a una valutazione delle parti finite della correzione al decadimento del μ. Poiché in tale decadimento la massa del mesone vettoriale è molto più grande dell'impulso trasferito, le correzioni alle grandezze osservabili, come lo spettro dell'elettrone, differiscono appena dalle correzioni corrispondenti nella teoria locale; infatti le ulteriori correzioni radiative sono di ordine αm²μ/m²_W, che è assolutamente trascurabile al livello attuale di precisione sperimentale. Le correzioni alle quantità integrate, come la vita media e forse anche il parametro ξ (che misura l'asimmetria integrata), sono, in linea di principio, più interessanti delle altre; tuttavia, le correzioni alla vita media sono fisicamente importanti soltanto se si paragona il tasso di decadimento del muone con un secondo processo accuratamente misurato che permetta anch'esso una valutazione precisa delle correzioni radiative. La stima delle correzioni al rapporto G_ν/G_μ (G_ν è la costante di accoppiamento vettoriale nel decadimento β) nel modello di S-W a quattro sapori fornì dei risultati in discreto accordo con l'universalità di Cabibbo; tali valutazioni sono poi state estese anche alla versione a sei sapori del modello e anche per esse vale la conclusione qualitativa cui si era giunti in precedenza, ossia che è necessario includere le correzioni radiative a un anello perché rimanga valida l'universalità osservata delle interazioni deboli.

Per valutare alcune delle parti finite in tutte le applicazioni delle teorie di gauge che coinvolgono gli adroni, si fanno due ipotesi importanti: a) che i coefficienti dei termini dominanti nello sviluppo alle piccole distanze del prodotto T-ordinato di due correnti presentino un comportamento approssimativamente del tipo di quello della teoria di campo libero, per lo meno nella regione spaziale che dà il maggior contributo agli integrali sui momenti virtuali; b) che i termini di ordine α(m²/m²_W), dove m rappresenta una massa adronica tipica oppure la massa di un quark, siano di ordine G_F, anziché di ordine α, e possano perciò, nella maggior parte dei casi, essere trascurati. L'ipotesi a) è interessante, ma speculativa, e si può giustificare meglio, in una teoria asintoticamente libera delle interazioni forti, con l'ipotesi supplementare che il comportamento asintotico inizi a impulsi k ≪ m_W. Una caratteristica interessante di questi calcoli è che, in virtù di tali ipotesi, le correzioni al rapporto G_ν/G_μ sono le stesse che si avevano nei vecchi calcoli locali, con un taglio a Λ = m_Z. Poiché in questi modelli m_Z ≿ 74,6 GeV, si ottiene che le correzioni sono necessariamente molto grandi.

Lo studio delle correzioni radiative nelle teorie di gauge ha anche posto l'accento sul concetto di naturalezza delle simmetrie e delle relazioni all'ordine più basso. Una teoria di gauge spontaneamente rotta si dice strettamente rinormalizzabile se contiene tutti i possibili termini gauge-invarianti, di dimensione ≤ 4, costruiti con i campi fondamentali della teoria stessa e compatibili con aitre simmetrie della lagrangiana: una tale teoria contiene tutti i controtermini necessari per la rinormalizzazione. Si definisce artificiale una simmetria o una relazione che si ottiene all'ordine più basso in α per valori particolari dei parametri della teoria. Una simmetria o una relazione si dice invece naturale se vale all'ordine più basso per valori arbitrari dei parametri di una teoria di gauge strettamente rinormalizzabile. L'importanza di tale concetto sta nel fatto che, se una certa relazione naturale tra i parametri della teoria vale all'ordine più basso in α, le correzioni a questa relazione dovute agli ordini superiori sono calcolabili, poiché non ci sono controtermini possibili che possano modificarla. Un esempio semplice è fornito dalle correzioni all'universalità elettronemuone e dalla relazione e^{2 =} g²(1 − m²_W/m²_Z) + O(α) nel modello originale di S-W. In particolare, sono state studiate in dettaglio le deviazioni di ordine α dall'universalità elettrone-muone nei decadimenti leptonici dei mesoni W ed è stata messa in evidenza la relazione tra i risultati ottenuti e i teoremi sulla cancellazione delle singolarità di massa.

Un problema generale che si presenta in qualsiasi teoria che cerchi di unificare le interazioni elettromagnetiche e quelle deboli è rappresentato dalla possibilità di violazioni all'ordine α della parità, della stranezza e, probabilmente, anche del charm. Weinberg ha compiuto uno studio generale di questo problema, che si applica a modelli di gauge in cui le interazioni forti sono mediate da gluoni non abeliani (v. Weinberg, 1973) accoppiati alle correnti di un gruppo di gauge forte G_forte che commuta con il gruppo di gauge debole G_deb associato alle correnti elettromagnetiche e deboli.

All'ordine zero in α, in questa classe di teorie, le simmetrie approssimate delle interazioni forti (quali l'isospin, SU(3), SU(2)_L ⊗ SU(2)_R e così via) sono rotte soltanto dai termini di massa dei quarks. Inoltre Weinberg ha dimostrato che anche le correzioni di ordine α derivanti dalle interazioni deboli (da non confondere con quelle di ordine α(m²/m²_W) che si considerano di ordine G_F) si manifestano solo sotto forma di correzioni alla matrice di massa dei quarks. L'assenza di correzioni di ordine α alla parità, alla stranezza e al charm è dunque una conseguenza delle seguenti osservazioni: a) una matrice di massa arbitraria (che comporta in generale matrici γ₅) può essere diagonalizzata da trasformazioni unitarie indipendenti sui campi destrogiri e levogiri dei quarks; b) nella classe di teorie che stiamo analizzando tali trasformazioni lasciano invariati tutti gli altri termini nella lagrangiana delle interazioni forti. Sarà forse interessante notare che il modello delle interazioni forti di cui ci si è serviti nell'analisi che abbiamo discusso in precedenza delle correzioni ai decadimenti semileptonici è un particolare esempio della classe generale di modelli postulati da Weinberg (v., 1973) nella sua discussione della conservazione della parità e della stranezza.

Per comprendere l'importanza dell'analisi di Weinberg, bisogna tener presente che le correzioni radiative deboli all'ordine più basso denvanti da grafici di Feynman individualmente convergenti, in una gauge rinormalizzabile, sono necessariamente di ordine G_F; il fatto che esse non si possano mai promuovere all'ordine α segue immediatamente dal comportamento di tali grafici ad alto m_W, comportamento che è ~ (1/m²_W) a meno di potenze di ln m²_W. La possibilità che vi sia un effetto debole confrontabile con quelli elettromagnetici può verificarsi se ci si imbatte in grafici divergenti. In questo caso bisogna distinguere fra tre possibilità, ossia: a) che le divergenze da vari grafici non si cancellino a vicenda, ma possano essere assorbite in parametri aggiustabili (questa è la situazione tipica che si presenta in una teoria non naturale, situazione tutt'altro che soddisfacente dal punto di vista estetico); b) che il sistema sia vincolato in maniera tale che non si possano introdurre i controtermini necessari per assorbire le divergenze; in questo caso le divergenze derivanti da vari grafici di Feynman devono cancellarsi a vicenda. Le parti finite saranno perciò della forma α ln (m²/m²_W); se anche questi termini non si cancellano e coinvolgono violazioni della parità e della stranezza, la teoria dovrà presumibilmente essere scartata per motivi sperimentali; c) che il sistema abbia una simmetria più alta che permetta di eliminare semplicemente con una trasformazione tutti gli effetti deboli indesiderati di ordine a il fatto che le divergenze si cancellino a vicenda oppure no diventa dunque irrilevante. Questa è la situazione prospettata da Weinberg; nella sua analisi la simmetria più alta è quella chirale associata agli accoppiamenti tra gluoni e fermioni.

Nel paragrafo b, 1, abbiamo osservato che il rapporto Γ(K_L → μ⁺ + μ^-)/Γ(L_L → tutto) è molto piccolo. Il valore riportato nell'equazione (12) fa scartare automaticamente quei modelli in cui un mesone vettoriale neutro è accoppiato, all'ordine più basso, sia alla corrente adronica con ΔQ = 0, ΔS = 1, sia alla corrente leptonica neutra. Nei modelli in cui le correnti ΔQ = 0, ΔS = 1 non sono accoppiate all'ordine più basso, il processo K_L → μ⁺ + μ^- può ancora verificarsi attraverso gli effetti degli ordini superiori. L'effetto debole dominante nasce dalla sequenza (virtuale) K_L → W⁺W^- → μ⁺μ^-. Calcoli specifici e valutazioni di ordine di grandezza mostrano che in quei modelli che non incorporano il meccanismo GIM (v. Glashow e altri, 1970) il rapporto Γ(K_L → μ⁺ + μ^-)/Γ(K_L → tutto) è di ordine α² ≃ 10^-4, che è ancora troppo grande; ciò costituisce un forte indizio per ritenere che queste teorie non siano accettabili. Nelle teorie che incorporano il meccanismo GIM si trova, invece, Γ(K_L → μ⁺ + μ^-)/Γ(K_L → tutto) = O (αΔm²/m²_W)², dove Δm² è la differenza tra i quadrati delle masse dei quarks con charm e di quelli ordinari; questo valore è compatibile con risultati sperimentali, se Δm²/m²_W ≾ α. Questo risultato è importante anche in relazione ai tentativi recenti di originare il meccanismo di Higgs in una maniera dinamica (v. i contributi di Bég, 1980; v. Bég, 1981).

Recentemente sono stati fatti studi specifici sull'effetto delle correzioni radiative alla determinazione fenomenologica di sen² θ_W e dei valori precisi di m_W e di m_Z, due parametri che sono importanti per una verifica definitiva del modello di S-W. Per un'analisi dettagliata rimandiamo il lettore agli articoli citati in Bég e Sirlin, 1982; qui ci limiteremo soltanto a citare alcuni risultati:

Il dato sperimentale di partenza nell'equazione (89) è il rapporto tra le sezioni d'urto

dove N è un bersaglio isoscalare.

I valori numerici nelle equazioni (89-91) vanno confrontati con i valori citati in precedenza, ossia quelli delle equazioni (86-88).

3. Libertà asintotica.

L'attenzione rivolta alle teorie di gauge portò alla scoperta che le teorie di gauge non abeliane basate su gruppi di Lie semisemplici sono asintoticamente libere (v. Politzer, 1973; v. i contributi di Gross e Wilczek, 1973) e sono le uniche a esserlo; infatti nessun'altra teoria rinormalizzabile possiede questa proprietà (v. Coleman e Gross, 1973; v. Zee, Study of.., 1973). Sebbene la ricerca della libertà asintotica sia stata promossa dalla necessità di trovare una teoria realistica delle interazioni forti - senza questa libertà, infatti, non si può dare un fondamento al modello dei partoni rimanendo nell'ambito della teoria dei campi -, le sue conseguenze sulle interazioni deboli sono assai interessanti, e in effetti abbiamo già avuto modo di notarne alcune nel corso della nostra analisi degli effetti di ordine α.

Il comportamento asintotico delle teorie di campo rinormalizzabili è descritto sinteticamente dall'equazione del gruppo di rinormalizzazione (v. Gell-Mann e Low, 1954; v. Callan, 1970; v. Symanzik, 1970 e i contributi del 1971), che per le teorie con un solo campo è

dove Γ⁽ⁿ⁾_ASI è la Parte asintotica, nel senso che spiegheremo in seguito, della funzione di Green rinormalizzata a n punti, irriducibile per una particella (cioè che non si può separare in due parti connesse tagliando una sola linea interna); β(g) e γ(g) sono funzioni della costante di accoppiamento rinormalizzata, g, e m è la massa rinormalizzata, oppure, nel caso di particelle prive di massa, il valore dell'impulso euclideo al quale si rinormalizza la teoria.

Se si pone p_i = λqi⁰, dove i q_i⁰ sono momenti non eccezionali fissi, Γ⁽ⁿ⁾_ASI si ottiene per definizione dalla somma di tutti i termini dominanti per λ → ∞ nella funzione di Green esatta Γ⁽ⁿ⁾, trascurando i termini che decrescono più rapidamente di Γ⁽ⁿ⁾_ASI per potenze di λ, a qualsiasi ordine finito nella teoria delle perturbazioni; con questa definizione, si può derivare l'equazione (93) dalle equazioni di Callan e Symanzik (v. Gell-Mann e Low, 1954; v. Callan, 1970; v. Symanzik, 1970 e i contributi del 1971) della teoria. Una serie di momenti q_i⁰ viene detta non eccezionale se Γ⁽ⁿ⁾(g • λm; q1⁰) = O[(ln λ)^c] vale per λ → o a tutti gli ordini della teoria delle perturbazioni rinormalizzata, con c che rappresenta una costante che dipende dall'ordine. I momenti euclidei sono non eccezionali se non si annulla alcuna somma parziale dei momenti. Per quanto riguarda i momenti di Minkowski, invece, la situazione è più complessa (v. Symanzik, 1970 e i contributi del 1971).

La soluzione dell'equazione (93) si può scrivere nel modo seguente

dove t = ln λ, D è la dimensione (in unità di massa) di Γ⁽ⁿ⁾ e à è la costante di accoppiamento invariante o effettiva definita da

Perciò

Se β(g′) ha uno zero di ordine intero a g′ = g_f, è chiaro che à → g_f quando t → + ∞ (− ∞), se [β(g′)/(g′ − g_f)] 〈 0 (> 0) per tutti i g′ tra g e g_f. Se il limite g_f si ottiene per t → + ∞ (− ∞), si dice che esso è un punto fisso stabile ultravioletto (infrarosso) del gruppo di rinormalizzazione. (La struttura analitica di β(g) è tuttora ignota. A qualunque ordine finito della teoria delle perturbazioni, β è ovviamente un polinomio e gli zeri qui considerati sono sufficienti per la nostra discussione; si deve tuttavia essere consapevoli che le proprietà derivate dalla teoria delle pertubazioni possono rivelarsi alquanto fuorvianti). Se g è prossimo a uno zero stabile ultravioletto, il comportamento asintotico è dato da

purché l'integrale converga. Perciò il comportamento ultravioletto è controllato da λ^D-nγ(gf) oppure, equivalentemente, dalla dimensione anomala γ(g_f) valutata al punto fisso. In questo caso, si dice che la costante di accoppiamento g è nel campo di attrazione del punto stabile fisso ultravioletto g_f.

A qualsiasi ordine finito della teoria delle perturbazioni, β(g) ha uno zero all'origine, g = 0, corrispondente al limite del campo libero. Se [β(g′)/g′] 〈 0 (> 0) nell'intervallo (0, g), lo zero è ultravioletto (infrarosso) stabile. In due lavori separati, Politzer, da una parte, e Gross e Wilczek, dall'altra, fecero un'importante osservazione, cioè che per una vasta classe di teorie di gauge non abeliane l'origine è effettivamente un punto stabile ultravioletto (v. Politzer, 1973; v. Gross e Wilczek, Ultraviolet behavior..., 1973). In quel caso, quando λ → ∞, Γ(A%$Sn%I)%≈ λ^D, a meno di correzioni logaritmiche. (Nelle teorie asintoticamente libere, l'integrale nell'equazione (97) non converge: l'integrando si comporta come (1/t′) per t′ grande, per cui l'esponenziale contribuisce con un fattore (ln λ)^c in Γ(A%$Sn%I)%; v. Gross e Wilczek, Asymptotically free..., 1973; v. Georgi e Politzer, 1974). Perciò, a meno di tali correzioni, Γ⁽ⁿ⁾_ASI si avvicina al comportamento della teoria di campo libero, purché, naturalmente, g sia nel campo di attrazione dell'origine e non invece di qualche altro punto fisso stabile ultravioletto.

Le equazioni del gruppo di rinormalizzazione si possono applicare per studiare il comportamento per λ → 0 dei coefficienti C⁽ⁿ⁾(x, g) nello sviluppo operatoriale del prodotto delle correnti (v. Christ e altri, 1972), che, a sua volta, controlla le proprietà della diffusione inelastica profonda leptone-adrone. Il comportamento dell'annichilazione e⁺e^- ad alte energie è controllato soltanto dal coefficiente dell'operatore unità nel prodotto delle correnti elettromagnetiche e può essere anch'esso studiato mediante la tecnica del gruppo di rinormalizzazione.

Un'analisi della diffusione inelastica profonda dimostra che: a) con ogni probabilità l'ipotesi dell'invarianza di scala è violata dalle potenze di q², a meno che la teoria non sia asintoticamente libera (v. Parisi, 1973); b) le teorie asintoticamente libere presentano tale invarianza, a meno di correzioni logaritmiche (v. Gross e Wilczek, Asymptotically free..., 1973; v. Georgi e Politzer, 1974). Per l'annichilazione e⁺e^-, nelle teorie asintoticamente libere, il limite di invarianza di scala viene raggiunto esattamente ed è anche possibile calcolare la prima correzione all'ordine dominante (v. Appelquist e Georgi, 1973; v. Zee, Electron-positron..., 1973).

Non è perfettamente chiaro se gli effetti asintotici che abbiamo fin qui esposti abbiano una qualche relazione con l'invarianza di scala precoce che si osserva nelle reazioni e^- + N → e^- + ... e ν_μ + N → μ^- + ... . Ciononostante, lo sforzo di comprendere l'invarianza di scala nel contesto della teoria dei campi ortodossa ha condotto allo studio delle teorie asintoticamente libere delle interazioni forti. È chiaro, naturalmente, che lo studio della dinamica asintoticamente libera degli adroni è abbastanza interessante di per sé, da un punto di vista teorico, da sopravvivere alle possibili rotture dell'invarianza di scala alle energie accessibili ai nuovi acceleratori.

4. Teoria di gauge delle interazioni forti: cromodinamica quantistica.

a) Caratteristiche generali.

Un elegante procedimento per generare le interazioni forti in un modo asintoticamente libero consiste nell'associare una simmetria di gauge al grado di libertà di colore proprio dei quarks. La teoria di gauge SU(3)_C che si basa su tale procedimento ed è detta cromodinamica quantistica (QCD) (v. Politzer, 1974; v. Marciano e Pagels, 1978; v. Mueller, 1981) ha finito per essere universalmente accettata come l'unica teoria delle interazioni forti, sebbene molti problemi teorici debbano ancora essere risolti prima di poter asserire che tale teoria descriva tutti gli aspetti della fisica delle interazioni forti. Il fatto che la QCD sia stata accettata così rapidamente è dovuto alle sue qualità estetiche, oltre che a proprietà più tangibili che elencheremo in seguito. Elencheremo anche alcune delle ipotesi che si devono tuttora fare circa le soluzioni delle equazioni della QCD, perché queste siano conformi ai fatti osservati.

La teoria è definita dalla lagrangiana

dove

è il rotore di Yang e Mills dei campi dei gluoni Aμ^α (α = 1, 2,..., 8), f^αβδ sono le costanti di struttura del gruppo SU(3), f è l'indice di sapore dei fermioni e

è la derivata covariante nello spazio dei campi ψ. Questi ultimi si trasformano secondo la rappresentazione tridimensionale del gruppo di colore; λ^α/2 sono le matrici della rappresentazione corrispondente dell'algebra di SU(3):

Nelle equazioni (99) e (100), g₀ è una costante di accoppiamento. Infine, ℒ_G.F. e ℒ_F.P. nell'equazione (98) sono rispettivamente il termine che fissa la gauge e il termine corrispondente ai fantasmi di Faddeev e Popov (v., 1967): il primo deve essere specificato per quantizzare la teoria, mentre il secondo è necessario per derivare le corrette regole di Feynman. L'intera lagrangiana, compresi questi due ultimi termini, è invariante sotto le trasformazioni infinitesime di Becchi, Rouet e Stora (v., 1974).

La caratteristica più interessante della lagrangiana della QCD è che (con una sola notevole eccezione, di cui ci occuperemo in seguito) essa incorpora tutte le simmetrie conosciute delle interazioni forti, ossia: 1) la conservazione del numero barionico; 2) le simmetrie approssimate di isospin [SU(2)] e di SU(3). Queste diventano esatte rispettivamente nei limiti m_u = m_d e m_u = m_d = m_s; 3) la conservazione parziale delle correnti assiali (PCAC) e della simmetria chirale.

Nel limite m_f → 0, per tutti gli f; il gruppo di invarianza globale di ℒ si estende dall'U(1)_V del numero barionico al gruppo

G = U(1)_V ⊗ U(1)_A ⊗ SU(N_F)_L ⊗ SU(N_F)_R, (102)

dove N_F è il numero di sapori dei quarks. Ci occuperemo in seguito del fattore U(1)_A, dei problemi che esso pone e della maniera in cui questi si risolvono. Gli ultimi due fattori contengono i gruppi chirali, che abbiamo già incontrato nella fenomenologia delle interazioni forti, ossia SU(2)_L ⊗ SU(2)_R, SU(3)_L ⊗ SU(3)_R e così via. Questi gruppi sono generati dalle cariche (α = 1, ..., N²_F − 1)

dove F^α sono le matrici che rappresentano i generatori di SU(N_F) nella rappresentazione cui appartengono i campi ψ. Le cariche sono associate alle correnti conservate

Si noti che quando le masse m_f sono diverse da zero, le correnti assiali non sono più conservate, ma soddisfano ancora la definizione di Wilson (v. Bernstein e altri, 1960; v. Kuang-Chao Chou, 1961; v. Wilson, 1969) di conservazione parziale.

b) QCD perturbativa e fenomeni alle piccole distanze nella dinamica adronica.

Il gruppo di rinormalizzazione esprime una proprietà fondamentale delle teorie di campo rinormalizzabili, che si può parafrasare nella maniera seguente: se una quantità ammette uno sviluppo perturbativo nelle potenze di una costante di accoppiamento rinormalizzata g(μ₁)², lo sviluppo può sempre essere riespresso per mezzo di un'altra costante di accoppiamento rinormalizzata g(μ₂)²; in particolare, se nel problema esiste una distanza piccola ρ o un grande momento q ~ 1/ρ, si può usare, come parametro di sviluppo, à², cioè la costante di accoppiamento effettiva definita dall'equazione (95); se la teoria è asintoticamente libera, i primi termini dello sviluppo dovrebbero quindi bastare per approssimare la quantità analizzata. La QCD è perciò soprattutto adatta per descrivere i fenomeni adronici a piccole distanze, e in questo campo ha avuto un notevole successo. In tutte quelle situazioni in cui ha senso paragonare la teoria con i risultati sperimentali si è trovato che non esiste alcun conflitto.

Per la QCD con N_F sapori,

Perciò, se definiamo

dall'equazione (96) segue

La massa A è un parametro libero nella QCD perturbativa. D'ora in poi, ogni volta che vorremo ottenere un suo valore esplicito, prenderemo

Λ ≈ 300 MeV. (112)

I più grandi successi della QCD perturbativa sono stati i seguenti.

1. Le violazioni dell'invarianza di scala nella diffusione inelastica profonda leptone-adrone. La sezione d'urto differenziale per il processo

l(k_i) + N(p_i) → l(k_f) + adroni (113)

può essere scritta nella maniera seguente:

dove x = ∣ q² ∣/2 Mν, y = ν/E, q = k_i − k_f, M² = pi², k_i • p_i = EM e q • p_i = νM. I valori di x e di y consentiti dalla conservazione dell'energia e del momento sono dati dalle equazioni (114) e (115). F₁ e F₂ sono le consuete funzioni di struttura per le quali Bjorken aveva congetturato che fosse

F₂(x, y) ≡ F₂(x) (117)

F₁(x, y) ≡ F₁(x). (118)

Per spiegare il fatto che le funzioni di struttura sono indipendenti da y, fatto confermato da esperimenti effettuati a ∣ q² ∣ relativamente basso [~ (pochi GeV)²], Feynman e altri inventarono il modello a partoni. La QCD, invece, prevede una leggera dipendenza da y, tale però che sia

Gli esperimenti effettuati a valori maggiori di ∣ q² ∣ sono in accordo con la QCD (Mess e Wiik, 1982).

2. L'invarianza di scala nell'annichilazione e⁺e^-. La previsione della QCD per la sezione d'urto si può scrivere nella maniera seguente:

dove la sommatoria è estesa ai quarks di ogni sapore e la costante di accoppiamento effettiva è definita come nell'equazione (110), con q² = (energia nel c. d. m.)².

I risultati sperimentali ottenuti con l'anello di accumulazione PETRA (Mess e Wiik, 1982), a energie nel centro di massa ~O(30 GeV), sono in buon accordo con l'equazione (120); la presenza del termine (α_S/π) è suggerita dai dati, sebbene soltanto al livello di una deviazione standard.

3. I getti (jets) nell'annichilazione e⁺e^-. Il fenomeno e⁺e^- → due getti adronici, che si osserva, viene interpretato nella QCD come risultato del processo e⁺e^- → qö; lo spin 1/2 dei quarks richiede quindi una distribuzione angolare del tipo

dove θ è l'angolo che l'asse del getto forma con la direzione dei fasci e⁺e^- nel centro di massa. L'equazione (121) è ampiamente confermata dagli esperimenti (Mess e Wiik, 1982).

Il processo seguente, in ordine di complessità, nella QCD perturbativa è ovviamente e⁺e^- → qög (dove g indica un gluone), che dà origine a tre getti adronici; eventi a tre getti sono stati effettivamente osservati e analizzati, e si è trovato che le loro proprietà sono compatibili con la QCD (Mess e Wiik, 1982).

4. Le algebre anomale, le regole di somma per neutrini ecc. I commutatori delle componenti spaziali delle correnti di sapore, come, per esempio, Jm^α(x) = ψ-(x)γ_m (1/2) λ^αψ(x) (dove λ^α è una matrice nello spazio dei sapori), danno origine a un'abbondante messe di regole di somma. Tali regole sono tuttavia scarsamente attendibili, poiché i commutatori delle correnti, definiti dal procedimento di Johnson, Low e Bjorken (v. Johnson e Low, 1966; v. Bjorken, 1966), non coincidono con i commutatori che si ottengono mediante banali manipolazioni effettuate sugli operatori di campo nei modelli teorici più semplici, quale il modello con gluoni abeliano; si è però dimostrato che tale discrepanza sparisce nella QCD e che, in questo senso, tutta una classe di algebre anomale diventa normale (v. Bég, 1975).

L'esempio più noto di algebra che veniva un tempo considerata anomala è costituito dall'algebra associata a tre sapori (v. Feynman e altri, 1964): U(6) ⊗ U(6). La QCD permette di definire tale algebra (v. Bég, 1975) e le regole di somma ad essa associate, che, sia detto per inciso, sembrano essere soddisfatte sperimentalmente.

5. La risoluzione del problema dell'U_A(1). Questo problema (Gell-Mann, 1969) risale a un'epoca precedente l'introduzione della QCD e ha le sue origini nella conservazione della corrente assiale del numero barionico nel limite in cui SU(2)_L ⊗ SU(2)_R è una simmetria esatta delle interazioni forti. Quando la simmetria chirale viene realizzata nel modo di Nambu e Goldstone, ciò significa che nel limite di SU(2) ⊗ SU(2) ci dovrebbero essere quattro bosoni di Goldstone; quando la simmetria viene rotta dai termini di massa dei quarks, tutti e quattro dovrebbero acquistare delle masse paragonabili tra loro, mentre si osservano soltanto tre mesoni leggeri che approssimano i bosoni di Goldstone, ossia i pioni.

Al livello superficiale, tale problema si ripresenta nella QCD. Tuttavia, la corrente assiale del singoletto di sapore, corrente che è gauge-invariante, non è conservata nella QCD a causa dell'anomalia di Bell, Jackiw e Adier (v. Bell e Jackiw, 1969; v. Adier, 1969):

dove C è una costante numerica conosciuta. (Un fattore di g² - dove g è la costante di accoppiamento nuda della QCD - è stato assorbito in FFè). Il generatore delle trasformazioni U_A(1) soddisfa quindi la

e non è una costante del moto se l'integrale dell'equazione (123) è diverso da zero.

Ora FFè può essere espresso come una quadridivergenza ed è facile verificare che per qualsiasi configurazione del campo che possa essere realizzata nella teoria delle perturbazioni, attorno Aμ^α = 0, si ha ΔQ_{A =} 0. Per risolvere il problema dell'U_A(1) nella QCD, è necessario perciò controllare se esistano delle soluzioni non perturbative delle equazioni di campo di Yang e Mills che possano dare ΔQ_A ≠ 0. Soluzioni di questo tipo (v. ‛t Hooft, Symmetry breaking..., 1976; v. Callan e altri, 1978), dette ‛istantoni', sono state effettivamente trovate; gli istantoni sono caratterizzati da un numero quantico topologico, il cosiddetto numero di Pontrjagin, n:

La risoluzione del problema dell' U_A(1) sta a cavallo tra il campo ben noto della QCD perturbativa e quello relativamente incerto della QCD non perturbativa. Ci accingiamo ora a esaminare brevemente quest'ultima.

c) Prospettive della QCD non perturbativa.

Esiste un'intera classe di problemi da risolvere prima che si possa asserire che la QCD fornisca una descrizione completa dei fenomeni adronici; tra questi problemi, i principali sono i seguenti.

1. Il confinamento del colore e il confinamento dei quarks. Nella formulazione generalmente accettata, alla quale ci atteniamo, si considera SU(3)_C come una simmetria esatta della natura. Tutti gli adroni fisici sono ritenuti singoletti di SU(3)_C; perché tale immagine possa essere valida, è necessario che la QCD garantisca il confinamento permanente di tutti gli oggetti che portano un colore, siano essi gluoni o quarks. Tuttavia ciò non si verifica a ciascun ordine finito della teoria delle perturbazioni, né d'altra parte c'è alcuna ragione per cui debba verificarsi: si tratta di un fenomeno di portata relativamente lunga e alle grandi distanze g può diventare arbitrariamente grande, tanto da rendere inapplicabile la teoria delle perturbazioni.

Il confinamento ha il vantaggio di risolvere automaticamente il problema delle divergenze infrarosse, che in questo caso è assai più grave che nella QED.

2. La rottura spontanea della simmetria chirale nello spazio dei sapori. La simmetria chirale dei sapori, rotta spontaneamente - o, per dirla in altri termini, realizzata alla maniera di Nambu e Goldstone - nel limite m_f → 0, costituisce l'unica spiegazione razionale del successo dei teoremi sui pioni soffici proposti negli anni sessanta (v. Dashen, 1969 e 1971). La QCD deve, perciò, assicurare che le cariche definite dalle equazioni (102) e (103) soddisfino leggi di conservazione

ÓV^α = 0, ÓA^α = 0 (125)

e

ÓV^α ∣ 0> = 0, ÓA^α ∣ 0> ≠ 0, (126)

dove QV^α ≡ QR^α + QL^α, QA^α ≡ QR^α − QL^α. Se le cariche assiali conservate non annichilano il vuoto, devono esistere N²_F − 1 bosoni di Goldstone e i quarks devono avere una massa dinamica M, o massa di Nambu e Goldstone. Per comprendere che il meccanismo che porta all'equazione (126) è intrinsecamente non perturbativo, basta notare che M soddisfa un'equazione omogenea del gruppo di rinormalizzazione la cui soluzione nel limite di accoppiamento debole è

M ∝ μ exp (− c/g²), (127)

dove μ è il parametro di scala introdotto per definire le funzioni di Green della teoria, g è la costante rinormalizzata di accoppiamento della QCD e c è una costante positiva nota.

È possibile che le equazioni (126) e (127) valgano anche in presenza di istantoni (v. Callan e altri, 1978), ma su questo punto non tutti sono attualmente d'accordo. Nella sua analisi del problema della rottura spontanea della simmetria chirale, ‛t Hooft segue un metodo diverso (prospettato in una conferenza non pubblicata del 1979): egli considera dei fermioni privi di massa, sia elementari che composti, quali si avrebbero se la QCD scegliesse la realizzazione di Wigner e Weyl del gruppo chirale nello spazio dei sapori. Le anomalie di Beh, Jackiw e Adler (v. Belì e Jackiw, 1969; v. Adler, 1969) associate ai composti di quarks vengono poi identificate con le anomalie triangolari dei quarks: questa è una condizione del tutto plausibile per ogni teoria nella quale i nucleoni sono considerati come stati legati dei quarks. A queste condizioni sulle anomalie vanno aggiunte le cosiddette condizioni di ‛disaccoppiamento'.

La condizione di disaccoppiamento consiste nel richiedere che, se uno dei quarks è dotato di una grande massa associata alla corrente, tale cioè che il gruppo di sapori si riduca da SU(N_F)_L ⊗ SU(N_F)_R a SU(N_F − 1)_L ⊗ SU(N_F − 1)_R ⊗ U(1), tutte le particelle composte che contengono questo quark pesante diventino anch'esse pesanti, uscendo, perciò, o ‛disaccoppiandosi', dalla teoria. La formulazione di tale condizione, data da ‛t Hooft, parte dall'ipotesi tacita che la simmetria chirale rimanga valida anche se un quark diventa pesante: in altre parole, sia SU(N_F) che SU(N_F − 1)_L ⊗ SU(N_F − 1)_R ⊗ U(1) si realizzano entrambi nel modo di Wigner e Weyl, e le proprietà di trasformazione dei fermioni privi di massa sotto quest'ultimo gruppo non sono disturbate. Questa ipotesi si presta alle critiche per la semplice ragione che quando un quark diventa massiccio può benissimo dare inizio a una transizione di fase.

Fatte queste riserve, possiamo ora completare la nostra rassegna del metodo di ‛t Hooft: le due serie di condizioni danno luogo a un sistema algebrico che non ha soluzione, per cui si conclude che l'ipotesi iniziale sulla scelta della rottura spontanea della simmetria chirale nel settore dei sapori alla Nambu e Goldstone è errata. A prescindere dal verdetto finale che verrà dato sulla logica di ‛t Hooft, questa ha senz'altro portato a uno sviluppo assai interessante, ossia a una dimostrazione del fatto che la rottura spontanea del gruppo chirale, nella QCD con N_C colori, è possibile nel limite di N_C grande (v. Coleman e Witten, 1980). La validità di tale risultato per N_C = 3 deve essere tuttora considerata soltanto un'ipotesi. Si noti che anche f_π, ossia la costante di decadimento del pione, soddisfa un'equazione omogenea del gruppo di rinormalizzazione: la sua dipendenza da g è perciò identica a quella di M.

Passiamo ora a esaminare i termini di massa della lagrangiana. La massa m_f è quella che compare nei calcoli di algebra delle correnti e che, conformemente all'uso comune, si può chiamare ‛massa di corrente' (nella QCD, come anche nella QED, m_f ψ-_fψ_f è un operatore finito; la rinormalizzazione della massa è, perciò, moltiplicativa e banale e non faremo una distinzione esplicita tra massa nuda e massa rinormalizzata). La massa netta del quark, M_f, ossia la cosiddetta massa costituente, è una sovrapposizione della massa di corrente e di quella dinamica:

M_f = m_f + M + ... , (128)

dove i puntini indicano altri termini, quale la variazione della massa dinamica, provocata dalla presenza della massa di corrente.

In qualsiasi gauge specifica, una definizione precisa della massa dipendente dal momento del quark è data da

dove S′ è il propagatore rinormalizzato del quark. Si pensa che la componente dinamica di questa massa decresca rapidamente (ossia come una potenza di p) alle alte frequenze

mentre la componente di corrente varia soltanto in maniera logaritmica:

A è un parametro dinamico, mentre B può essere calcolato nella teoria delle perturbazioni. Le equazioni (130) e (131) permettono di chiamare M_f e m_f rispettivamente massa infrarossa e massa ultravioletta.

Se le m_f sono differenti da zero, i bosoni di Goldstone - che si possono identificare con i normali π, K e così via - acquistano massa. Naturalmente, il concetto di PCAC è assai utile per quei sapori per i quali m_f ≪ M. Dato che sappiamo che la PCAC è ben soddisfatta per i pioni, possiamo supporre che le masse costituenti dei quarks u e d ci forniscano una misura della massa dinamica M:

M ≈ 3f_π ≈ 300 MeV. (132)

L'equazione (132) fornisce la scala naturale della massa, Λ_C(≈ M), della QCD.

5. Il modello standard delle interazioni tra quarks e leptoni.

Gli sviluppi nella fisica teorica che abbiamo descritto nelle pagine precedenti vengono di solito riassunti con una terminologia divenuta ormai convenzionale.

Con l'espressione ‛QFD standard' intendiamo la teoria di gauge delle interazioni elettrodeboli tra quarks e leptoni, basata sul gruppo SU(2)_L ⊗ U(1) nell'ambito della metodologia canonica della QFD (ossia la rottura della simmetria alla maniera di Higgs e Kibble, con campi elementari di spin zero, per generare le masse, in particolare quelle dei campi di gauge accoppiati ai generatori rotti). La scelta delle rappresentazioni dei campi che compaiono nella teoria fa parte integrante della definizione della QFD normale. Il modello standard contiene dunque i quattro campi di gauge, W^±, Z e γ, un campo fisico di Higgs, ϕ, e tre generazioni di quarks e di leptoni.

Come abbiamo spiegato nel cap. 2, È d, i campi dei quarks con massa di corrente definita e i campi che si trasformano in maniera irriducibile sotto il gruppo di isospin debole non coincidono: questi ultimi sono quelli che compaiono nella lagrangiana al primo stadio di rottura della simmetria. È perciò necessaria una diagonalizzazione della matrice di massa dei quarks, la quale introduce nella teoria quattro parametri, ossia tre angoli del tipo di Cabibbo e una fase che viola CP (la stessa cosa avviene nel settore dei leptoni, se si attribuisce una massa ai neutrini). La QFD standard è dunque una teoria nella quale occorre determinare sperimentalmente i seguenti parametri: le sei masse dei quarks, le tre masse dei leptoni, le due masse dei campi di gauge, la massa del campo di Higgs, quattro angoli di mescolamento e la costante di struttura fine. Poiché possiamo, senza nulla perdere della generalità della teoria, scegliere le unità in maniera tale che una delle masse sia uguale a uno, si ha un totale di sedici parametri; dobbiamo però notare che tale conteggio è valido soltanto nell'ambito della teoria delle perturbazioni, mentre, come spiegheremo in seguito, gli effetti non perturbativi possono aggiungere un altro parametro.

Il modello standard è l'unione della QFD e della QCD, ossia la teoria basata sul gruppo di gauge SU(3)_C ⊗ SU(2)_L ⊗ U(1) con le assegnazioni dei campi alle rappresentazioni elencate più sopra.

Se CP non è un'invarianza esatta, la lagrangiana del modello standard conterrà, in genere, un termine supplementare (v., per es., Bég e altri, 1979) di dimensione 4:

dove F è il rotore di Yang e Mills del campo dei gluoni, Fè è il suo duale (v. eq. 122) e θ è un parametro sconosciuto. È assai facile dimostrare che δℒ non può contribuire ad alcun processo fisico, a nessun ordine della teoria delle perturbazioni. Nella QCD, tuttavia, gli effetti non perturbativi svolgono un ruolo essenziale; senza una ulteriore ipotesi non si può risolvere il ‛problema di CP forte', o, in altre parole, evitare di avere θ come parametro libero. A rigor di termini, vi sono due parametri del tipo di θ: uno per il gruppo SU(3)_L e un altro per SU(2)_L. Il modello normale è perciò caratterizzato da un totale di diciannove parametri, la maggior parte dei quali si ha nel settore della QFD. Le perplessità destate da tale eccesso di parametri sono all'origine di gran parte delle ricerche più recenti in questo campo.

6. Grande unificazione e sintesi SU(5).

I primi tentativi di andare al di là del modello standard, rimanendo tuttavia sempre nell'ambito della metodologia canonica, furono fatti già agli albori delle teorie di gauge: si trattava di includere il gruppo di gauge del modello in un gruppo semplice di rango ≥ 4, per combinare le interazioni forti, quelle elettromagnetiche e quelle deboli in una singola teoria grande unificata. Tra le numerose proposte allora avanzate, una ebbe subito maggior successo delle altre, ed è riuscita, almeno finora, a resistere alla prova del tempo: la sintesi SU(5) di Georgi e Glashow (v., 1974). Nell'analisi seguente della grande unificazione, della quale ci limiteremo a illustrare i concetti fondamentali, concentreremo la nostra attenzione proprio su questa proposta, poiché è la meglio definita.

Per farsi un'idea delle condizioni richieste al gruppo unificante SU(5), si tenga presente che, per ogni generazione di leptoni e di quarks, i campi di Fermi descrivono otto fermioni levogiri, sette fermioni destrogiri, otto antifermioni destrogiri e sette antifermioni levogiri. Georgi e Glashow proposero di porre i quindici oggetti levogiri di ogni generazione in una rappresentazione riducibile, somma diretta di due rappresentazioni irriducibili, una a cinque e l'altra a dieci dimensioni:

15 = 5* + 10 (134)

I vantaggi di tale schema sono i seguenti: 1) esso si riduce nel modo richiesto sotto SU(3)_C ⊗ SU(2)_L ⊗ U(1):

5* = (1, 2) ⊕(3*, 1), (135)

10 = (1, 1) ⊕ (3*, 1) ⊕ (3, 2), (136)

cosicché

(si tenga presente che la corrente debole si può considerare costruita a partire da fermioni levogiri oppure da antifermioni destrogiri); 2) esso è privo di anomalie.

Mediante una scelta opportuna dei parametri nel settore di Higgs - occorrono almeno 34 campi di Higgs, o addirittura 124 se si vuole rimuovere completamente la degenerazione nell'approssimazione ad albero -, si può fare in modo che la rottura spontanea della simmetria si verifichi in due passi successivi:

dove m_X ~ 10¹⁴ GeV. Nel primo passo è necessaria una rottura fortissima perché alcune transizioni veloci nel limite della simmetria del SU(5) - quale, ad esempio, la non conservazione del numero barionico - siano rallentate fino ai limiti imposti dall'osservazione.

Una conseguenza importante della grande unificazione è il fatto che il parametro nudo sen² θ0_W viene elevato dallo stato di costante non rinormalizzata infinita a quello di numero razionale definito. Per comprendere il fatto che sen² θ0_W è finito, basta scrivere sen² θ0_W = e0²/g²₂₀: poiché e₀ deve essere una combinazione lineare di g₁₀ e g₂₀, ossia delle costanti di accoppiamento dei sottogruppi SU(2)_L e U(1), e poiché la grande unificazione impone la condizione naturale g₁₀ = g₂₀ = g₃₀, ne consegue che il rapporto e²₀/g²₂₀ deve essere finito. Trovare il valore di sen² θ²_W è un semplice esercizio di teoria elementare dei gruppi e noi ci limiteremo perciò a riportare il risultato:

Formula

t₃ è la terza componente dell'isospin debole, Q è la carica elettrica di un fermione e n_g è il numero delle generazioni.

Il valore di sen² θ0_W è quello che si osserverebbe se SU(5) fosse una simmetria di gauge non rotta. In effetti, ci si avvicinerebbe a tale situazione se le energie fossero talmente grandi (≫ m_X) che si potesse trascurare la rottura di SU(5). Alle energie esplorate nei laboratori (≪ m_X), l'invarianza di SU(5) è, invece, malamente rotta: nell'intervallo m_W 〈 μ 〈 m_X il gruppo di gauge si riduce a SU(3)_C ⊗ SU(2)_L ⊗ U(1) e ci si deve attendere che le costanti di accoppiamento effettive dei tre sottogruppi varino in maniera diversa l'una dall'altra in tale intervallo, a causa di correzioni radiative molto grandi, di ordine [α ln (m_X/m_W)]ⁿ (n ≥ 1). In questo modello, le grandi differenze che si riscontrano tra gli accoppiamenti delle interazioni forti, di quelle deboli e di quelle elettromagnetiche sono dovute al fatto che i nostri esperimenti sono effettuati a energie molto al di sotto della scala di unificazione.

Un metodo potente per tener conto delle correzioni radiative è fornito dal gruppo di rinormalizzazione: tale metodo fu proposto inizialmente da Georgi, Quinn e Weinberg (v., 1974) e fu poi perfezionato da Marciano e Sirlin fino a includere le correzioni logaritmiche all'ordine superiore a quello dominante e gli effetti di ordine α (v. Marciano e Sirlin, 1981). Il risultato di tale analisi è, con buona approssimazione,

sen² θ_W = 0,218 + 0,004(N_H − 1), (141)

dove N_H è il numero di doppietti di Higgs leggeri (ossia con massa ≪ m_X). Per N_H ≤ 4, l'equazione (141) concorda perfettamente con i dati delle osservazioni.

Il calcolo della vita media del protone (v. Marciano e Sirlin, 1981) dà come risultato

τ_p = 10^-28±1(m_X in GeV)⁴, (142)

da paragonare all'attuale limite sperimentale (v. Cherry e altri, 1981)

τp^exp ≥ 6 × 10³⁰ anni. (143)

Se gli esperimenti ora in corso riveleranno l'esistenza del decadimento del protone (ad esempio, con τ_p ≤ 10³¹ ÷ 10³² anni), ciò costituirà un importantissimo successo per la grande unificazione basata su SU(5).

La terza previsione della sintesi SU(5) è che nel grande intervallo di energia 10² ÷ 10¹⁴ GeV vi sia un deserto privo di nuova fisica; molti studiosi, tra i quali anche l'autore del presente articolo, considerano tale aspetto assai implausibile.

Per esplorare la fisica che si apre alle energie dell'ordine di 10¹⁴ GeV ci si deve basare sulla cosmologia, per quanto riguarda i primi istanti successivi al big bang. Alle altissime temperature esistenti in quel momento dovevano aver luogo delle transizioni con violazione del numero barionico; nel caso che la violazione di CP sia abbastanza dura da resistere a tali temperature, le idee di Sakharov (v. Sakharov, 1967; v. Toussaint e altri, 1979) sulla genesi della asimmetria materia-antimateria nell'universo - a partire dalla configurazione simmetrica iniziale - potranno rivelarsi esatte. Tuttavia, a questo vantaggio potenziale notevolissimo della grande unificazione bisogna contrapporre la difficoltà rappresentata dalla probabile produzione di troppi monopoli magnetici superpesanti di ‛t Hooft e Polyakov (v. Poliakov, 1974; v. ‛t Hooft, 1974 e Magnetic charge..., 1976) nel periodo successivo alla creazione (v. Kibble, 1976; v. Preskill, 1979).

7. Critica della metodologia.

Una caratteristica della QFD convenzionale è la necessità di usare campi elementari di spin zero per stabilire la gerarchia delle simmetrie di gauge che determinano la fisica: questo modo di utilizzare il meccanismo di Higgs è stato usato nella maggior parte degli schemi che combinano la QFD e la QCD nell'ambito di una teoria grande unificata (GUT), ed è proprio ciò che abbiamo chiamato ‛metodologia canonica'. Il fatto che tale procedimento non sia del tutto soddisfacente risulta chiaro dalle seguenti osservazioni.

1. per stabilire una gerarchia di gruppi di gauge

G_n ⊃ G_n-1 ⊃ ... ⊃ G₁, (144)

a) si parte da un insieme di campi di Higgs; b) li si accoppia in maniera allo stesso tempo rinormalizzabile e invariante rispetto a G_n; c) si scelgono i parametri del potenziale di Higgs in modo tale che si abbia una rottura ‛spontanea' della simmetria, che produca dei bosoni privi di massa, i cui numeri e le cui proprietà di trasformazione corrispondano a quelli dei generatori rotti, cosicché possano essere tutti riassorbiti; infine d) si richiede che questa scelta di parametri fornisca una gerarchia di costanti di Goldberger e Treiman per gli ipotetici bosoni di Goldstone,

fn² > f²_n-1 > ... > f2², (145)

dove f_m indica simbolicamente la costante associata a quei bosoni che danno luogo a una rottura della simmetria da G_m a G_m-1; la gerarchia dell'equazione (145) porta, perciò, a quella dell'equazione (144) con G₁ non rotto al livello albero. In effetti, occorre verificare che questo edificio non crolli in presenza delle correzioni radiative o di effetti intrinsecamente non perturbativi; mentre le prime si possono calcolare, questi ultimi non si prestano ad alcun trattamento sistematico.

Se questo modello di rottura della simmetria si dimostrasse stabile anche dopo l'inclusione di effetti di ordine superiore, esso sarebbe ‛naturale'. Tuttavia, bisogna tener presente che, quando si introduce il campo elementare di Higgs, parole quali ‛spontaneo' - per descrivere una rottura della simmetria così accuratamente calibrata - e ‛naturale' si possono usare soltanto nel loro significato tecnico: la comprensione dei concetti espressi da tali aggettivi sfugge se ci si ferma al loro significato lessicale.

2. Nel modello standard, si parte da quattro campi reali con spin zero: tre di essi sono assorbiti nel meccanismo di Higgs, per cui rimane un solo campo fisico con spin zero. Ciò può sembrare economico, finché non ci si rende conto che sedici dei diciannove parametri indipendenti che caratterizzano il modello hanno origine nel settore di Higgs.

3. La situazione peggiora fino a diventare quasi drammatica se il modello standard viene incorporato in una teoria grande unificata.

Si consideri la sintesi SU(5), oggi di moda; la scelta più semplice di campi di Higgs che dà luogo alla catena

SU(5) → SU(3)_C ⊗ SU(2)_L ⊗ U(1) → SU(3)_C ⊗ U(1)_Q (146)

è quella di una rappresentazione 5 (complessa) e di una 24 (reale). Poiché quindici di tali campi dovranno essere assorbiti nel meccanismo di Higgs, restano diciannove campi fisici reali di Higgs. Il numero di parametri indipendenti è ventidue, superiore a quello del modello standard; di questi, ventuno hanno origine nel settore di Higgs. Purtroppo, la teoria con solo 5 + 24 campi di Higgs non pare basti a descrivere la realtà fisica: perché tutti i fermioni abbiano le masse indipendenti è necessario aggiungere una rappresentazione 45 (complessa); ciò darebbe un totale di 109 campi fisici di Higgs, con la corrispondente crescita del numero dei parametri.

Il tallone di Achille della realizzazione canonica di SU(5) è costituito dal problema della gerarchia dei gruppi di gauge. Vi sono due scale di massa distinte con (M²_W/M²_X) ~ 10^-24; per dar luogo a masse così disparate, i parametri del settore di Higgs, comprese le correzioni radiative, devono essere scelti con la precisione di una parte su 10²⁴. È chiaro che stiamo trattando di una caratteristica del modello che non è naturale, in alcun significato della parola.

Gruppi più grandi, quali SO(10) ed E₆, non portano alcun miglioramento, per quanto riguarda tali difficoltà; con E₆, per esempio, si deve partire da 650 campi di Higgs.

4. Wilson (cit. in Susskind, 1979) ha sottolineato una caratteristica insoddisfacente di tutte le teorie rinormalizzabili che hanno dei campi elementari di spin zero in quattro dimensioni: al contrario di tutte le altre divergenze, che sono logaritmiche, le autoenergie di particelle con spin zero divergono quadraticamente. La relazione tra masse nude e masse rinormalizzate è

μ² = μ²₀ − λΛ², (147)

dove Λ è un taglio ultravioletto e λ è il coefficiente del termine ϕ⁴ nella lagrangiana. Se, come suggerisce Salam (v., 1971), supponiamo che il taglio naturale si collochi in corrispondenza della massa di Planck, a Λ ~ 10¹⁹ GeV, la massa nuda, μ₀, dovrà essere scelta con la precisione di circa una parte su 10¹⁹, se vogliamo che μ sia dell'ordine di qualche GeV.

5. La libertà asintotica (v. Politzer, 1973; v. i contributi di Gross e Wilczek, 1973), che è una caratteristica molto interessante delle teorie di gauge basate su gruppi di Lie semisemplici, viene distrutta dalla presenza di campi elementari con spin zero.

La morale di ciò è dunque evidente: allorché si introducono nella lagrangiana dei campi di spin zero, si perdono irrimediabilmente alcune delle possibilità più interessanti che le teorie di gauge sembrano avere di avvicinarsi a una descrizione quantitativa delle interazioni tra le particelle elementari; in particolare sembra persa del tutto la semplicità della descrizione. Tale situazione impone che si riconsideri seriamente il suggerimento di scartare del tutto i campi elementari di Higgs per cercare di realizzare in maniera dinamica il meccanismo di Higgs (v. Bég e Sirlin, 1974; v. i contributi di Bég, 1980; v. Bég, 1981; v. Bég e Sirlin, 1982). Fino a oggi, però, non si dispone di alcun modello soddisfacente. Una caratteristica gradevole dello scenario dell'ipercolore, che è lo schema oggi più in voga, è la facilità con la quale esso fa rifiorire il deserto.

8. Problemi irrisolti; prospettive.

Abbiamo tracciato lo sviluppo della teoria delle particelle elementari durante gli ultimi dieci anni, con particolare riguardo alla nostra comprensione delle interazioni deboli. Nonostante progressi importanti, resi possibili dall'uso ragionato delle teorie di gauge nell'ambito concettuale fornito dalla teoria relativistica dei campi quantizzati, sussistono tuttora dei punti oscuri e dei problemi importanti che aspettano una soluzione. Nella nostra analisi abbiamo accennato ad alcuni di essi e di alcuni ci siamo occupati dettagliatamente; comunque, ci sembra opportuno riassumere brevemente le caratteristiche salienti di quelli che sembrano oggi i problemi principali.

1. Come abbiamo già ricordato nel cap. 5, il modello standard basato su SU(3)_C ⊗ SU(2)_L ⊗ U(1), con i suoi diciannove parametri liberi (o ventisei, se i neutrini hanno una massa), non si può considerare un modello di teoria fisica economica: esso ha uno scarsissimo potere di previsione, poiché, se è vero che è in accordo con i dati sperimentali nella regione limitata di energia che si può esplorare al momento attuale, non fornisce tuttavia una comprensione approfondita della dinamica, tale cioè da permetterci di fare un'estrapolazione attendibile alle energie più alte. Nel capitolo precedente ci siamo soffermati a lungo sui limiti della metodologia canonica; qualsiasi costruzione teorica che la utilizzi ne erediterà necessariamente i limiti. A questo problema, che sussiste da lungo tempo, ne va aggiunto un altro, che, negli ultimi tempi, è divenuto oggetto di analisi dettagliate: ci riferiamo al dibattito, tuttora in corso, sulla proliferazione dei fermioni elementari (v. tabella). La questione se una teoria che parte con ventiquattro fermioni possa, o meno, essere considerata una teoria di particelle elementari non può essere decisa semplicemente con il ragionamento; è chiaro, tuttavia, che la ricerca dell'economia nella descrizione della struttura della materia non ha avuto un grande successo. La questione non è, dunque, se si debba ricercare un'alternativa al modello standard, ma piuttosto quali siano le linee di ricerca che offrono le più grandi probabilità di fornire un'alternativa valida.

2. La grande unificazione, almeno nell'ambito di SU(5), oggi di moda, non porta miglioramenti reali ad alcuna delle difficoltà del modello standard: esso ci fornisce un valore per l'angolo rinormalizzato di Glashow, Salam e Weinberg, che è in accordo con le osservazioni, ma il prezzo che si paga è molto alto. Il numero dei parametri liberi, in effetti, cresce (sono ventidue nella versione minima, con neutrini privi di massa, e molti di più se si vogliono evitare le difficoltà derivanti dalle masse dei fermioni, aggiungendo un multipletto complesso con quarantacinque campi di Higgs) e cresce anche il numero di campi di spin zero finora non osservati. Inoltre, ci si presenta il problema di due scale di massa diverse, che differiscono l'una dall'altra di dodici ordini di grandezza: non si conosce alcuna ragione naturale che giustifichi tale gerarchia. Infine, c'è da domandarsi se un deserto esteso su un immenso intervallo di energia, 10² ÷ 10¹⁴ GeV, rappresenti una situazione fisica credibile.

3. Lo schema basato sull'ipercolore, per la rottura dinamica della simmetria e per la generazione di particelle composte di Higgs, fu proposto per risolvere i problemi posti dalla metodologia canonica; purtroppo, però, esso non è mai decollato veramente, e non si sa tuttora se si possano generare delle masse di corrente senza incorrere in difficoltà di qualche genere (v. Bég e Sirlin, 1982). Tuttavia, in assenza di rigorosi ‛teoremi di impossibilità, si può sperare che il problema possa essere superato con uno sforzo sufficiente.

4. I modelli fermionici composti rappresentano dei tentativi di risolvere il problema ddla proliferazione dei quarks e dei leptoni. Una delle difficoltà fondamentali, comune a un'intera classe di tali modelli, quelli che, peraltro, sembrano essere i più interessanti, è la loro incapacità di produrre le interazioni deboli dal principio di gauge a livello fondamentale, o livello della materia allo stato originale. La caratteristica essenziale dell'unificazione elettrodebole è costituita dal fatto che W^±, Z e γ si possono trattare nello stesso modo: tutti e quattro si comportano, per grandi momenti trasferiti, come campi di gauge privi di massa e forniscono, perciò, delle ampiezze sufficientemente convergenti da generare una teoria rinormalizzabile; è proprio in tale aspetto della formulazione canonica che sta il suo fascino estetico. La costruzione di schemi in cui γ è trattato in maniera differente dagli altri tre campi sembra non essere la strada giusta: ci troviamo anche qui in un campo in cui probabilmente non si è esercitata una sufficiente fantasia.

5. Al momento attuale, gran parte delle idee teoriche si basano su congetture relative al comportamento delle teorie del tipo della QCD nel settore non perturbativo (v. cap. 4, È c). I tentativi di dimostrare la validità di tali congetture, anche se rimanessero senza successo, sarebbero tuttavia utili, in quanto potrebbero aiutarci ad approfondire la nostra conoscenza nel settore.

6. Sarà utile ricordare che le nuove teorie non hanno finora risolto un vecchio problema della teoria delle interazioni deboli: perché nei decadimenti non leptonici vale la regola ∣ ΔI_forte ∣ = 1/2? Siamo passati dalle vaghe discussioni sul rafforzamento dell'ottetto al predominio del grafico ‛a pinguino' come possibile origine di tale rafforzamento (v. Bég e Sirlin, 1982), ma ciò non è certamente un gran passo in avanti.

7. La meta finale della fisica delle particelle è una descrizione unificata di tutte le interazioni: finché non si sarà riusciti a inserire nel quadro, in maniera convincente e rinormalizzabile, anche la gravità, la meta non potrà dirsi raggìunta.

(L'autore desidera ringraziare Judy Cuozzo e Carolyn Rhodes per l'aiuto prestato nella preparazione dell'articolo).

Bibliografia.

Abers, E., Lee, B. W., Gauge theories, in ‟Physical reports", 1973, IX, pp. 1-142.

Ademollo, M., Gatto, R., Nonrenormalization theorem for the strangeness-violating vector currents, in ‟Physical review letters", 1964, XIII, pp. 264-266.

Adler, S. L., Calculation of the axial-vector coupling constant renormalization in β decay, in ‟Physical review letters", 1965, XIV, pp. 1051-1055.

Adler, S. L., Axial-vector vertex in spinor electrodynamics, in ‟Physical review", 1969, CLXXVII, pp. 2426-2438.

Adler, S. L., Einstein gravity as a symmetry breaking effect in quantum field theory, in ‟Review of modern physics", 1982, LIV, p. 729 ss.

Appelquist, T., Georgi, H., e⁺e^- annihilation in gauge theories of strong interactions, in ‟Physical review", 1973, VIII, pp. 4000-4002.

Becchi, C., Rouet, A., Stora, R., The abelian Higgs Kibble model, unitarity of the S-operator, in ‟Physics letters", 1974, LII, pp. 344-346.

Bég, M. A. B., Electromagnetic induction of neutral lepton currents, in ‟Physical review", 1963, CXXXII, pp. 426-431.

Bég, M. A. B., Anomalous algebras and neutrino sum rules, in ‟Physical review", 1975, XI, pp. 1165-1170.

Bég, M. A. B., Dynamical Higgs mechanism and hyperhadron spectroscopy, in Recent developments in high energy physics. Proceedings of Orbis scientiae, 1980, Coral Gables (a cura di B. Kursunoglu, A. Perlmutter e L. F. Scott), New York 1980, pp. 23-42.

Bég, M. A. B., Dynamical symmetry breaking and hypercolor, in Proceedings of the XXth International conference on high energy physics, Madison, Wisconsin (a cura di L. Durand e L. Pondrom), New York 1980, pp. 489-492.

Bég, M. A. B., Composite models of quarks and leptons, dynamical symmetry breaking and hypercolour, in Proceedings EPS International conference on high energy physics, Lisbon, Portugal, 1981.

Bég, M. A. B., Bernstein, J., Sirlin, A., Questions pertaining to charge dependence of radiative corrections to superallowed fermitransitions, in ‟Physical review", 1972, VI, pp. 2597-2606.

Bég, M. A. B., Lee, B. W., Pais, A., Su(6) electromagnetic interactions, in ‟Physical review letters", 1964, XIII, pp. 514-517.

Bég, M. A.B., Maloof, D. J., Tsao, H. S., Strong P and T non invariances in a class of gauge theories, in ‟Physical review", 1979, XIX, pp. 2221-2226.

Bég, M. A. B., Singh, V., Splitting of spin-unitary spin supermultiplets, in ‟Physical review letters", 1964, XIII, pp. 418-421.

Bég, M. A. B., Sirlin, A., Gauge theories of weak interactions, in ‟Annual review of nuclear science", 1974, XXIV, pp. 379-449.

Bég, M. A. B., Sirlin, A., Gauge theories of weak interactions, in ‟Physics repoirts", 1982, LXXXVIII, p. 1 ss.

Bég, M. A. B., Tsao, H. S., Strong P and T noninvariances in a superweak theory, in ‟Physical review letters", 1978, XLI, pp. 278-281.

Behrends, R. E., Sirlin, A., Effect of mass splitting on the conserved vector current, in ‟Physical review letters", 1960, IV, pp. 186-187.

Bell, J., Jackiw, R., A PCAC puzzle: π⁰ → γγ in the σ-model, in ‟Nuovo Cimento", 1969, LX, pp. 47-61.

Bernstein, J. e altri, On the decay rate of the charged pion, in ‟Nuovo Cimento", 1960, XVII, pp. 757-766.

Bjorken, J. D., Application of the chiral U(6) ⊗ U(6) algebra of current densities, in ‟Physical review", 1966, CXLVIII, pp. 1467-1478.

Callan, C. G., Broken scale invariance in scalar field theory, in ‟Physical review", 1970, II, pp. 1541-1547.

Callan, C. G., Jr., Dashen, R., Gross, D. J., Toward a theory of the strong interactions, in ‟Physical review", 1978, XVII, pp. 2717-2763.

Carithers, W. C. e altri, Observation of the decay K0₁ → u⁺u^-, in ‟Physical review letters", 1973, XXX, pp. 1336-1340.

Cherry, M. L. e altri, Experimental test of baryon conservation: a new limit on the nucleon lifetime, in ‟Physical review letters", 1981, XLVII, pp. 1507-1510.

Christ, N., Hasslacher, B., Mueller, A., Light-cone behavior of perturbation, in ‟Physical review", 1972, VI, pp. 3543-3562.

Coleman, S., Gross, D., Price of axymptotic freedom, in ‟Physical review letters", 1973, XXXI, pp. 851-854.

Coleman, S., Weinberg, S., Radiative corrections as the origin of spontaneous symmetry breaking, in ‟Physical review", 1973, VII, pp. 1888-1910.

Coleman, S., Witten, E., Chiral-symmetry breakdown in large-N chromodynamics, in ‟Physical review letters", 1980, XLV, pp. 100-102.

Cornwall, J. M., Levin, D. N., Tiktopoulos, G., Uniqueness of spontaneously broken gauge theories, in ‟Physical review letters", 1973, XXX, pp. 1268-1270.

Dashen, R., Chiral SU(3) ⊗ SU(3) as a symmetry of the strong interactions, in ‟Physical review", 1969, CLXXXIII, pp. 1245-1260.

Dashen, R., Some features of chiral symmetry breaking, in ‟Physical review", 1971, III, pp. 1879-1889.

Faddeev, L.D., Popov, V. N., Feynamn diagrams for the Yang-Mills field, in ‟Physical letters", 1967, XXV, pp. 29-30.

Feynman, R. P., Gell-Mann, M., Theory of the Fermi interaction, in ‟Physical review", 1958, CIX, pp. 193-198.

Feynman, R. P., Gell-Mann, M., Zweig, G., Group U(6) ⊗ U(6) generated by current components, in ‟Physical review letters", 1964, XIII, pp. 678-680.

Fitch, V. e altri, Evidence for the 2π decay of the K0₂ meson, in ‟Physical review letters", 1964, XIII, pp. 138-140.

Friedman, D., Review of supersymmetry and supergravity, in Proceedings of the XIXth International confernece on high energy physics, Tokyo 1978, pp. 535-560.

Gell-Mann, M., Test of the nature of the vector interation in β decay, in ‟Physical review", 1958, CXI, pp. 362-365.

Gell-Mann, M., Symmetries of baryons and mesons, in ‟Physical review", 1962, CXXV, pp. 1067-1084.

Gell-Mann, M. e altri, Ameloration of divergence difficulties in the theory of weak interactions, in ‟Physical review", 1969, CLXXIX, pp. 1518-1527.

Gell-Mann, M., Low, F. E., Quantum electrodynamics at small distances, in ‟Physical review", 1954, XCV, pp. 1300-1312.

Georgi, H., Glashow, S. L., Unity of all elementary-particle forces, in ‟Physical review letters", 1974, XXXII, pp. 438-441.

Georgi, H., Politzer, H. D., Electroproduction scaling in an asymptotically free theory of strong interactions, in ‟Physical review", 1974, IX, pp. 416-420.

Georgi, H., Quinn, H., Weinberg, S., Hierarchy of interactions in unified gauge theories, in ‟Physical review letters", 1974, XXXIII, pp. 451-454.

Gerstein, S., Zeldovich, J., Meson corrections in the theory of beta decay, in ‟Journal of experimental and theoretical physics", 1956, II, pp. 576-582.

Glashow, S. L., Partial-symmetries of weak interactions, in ‟Nuclear physics. A", 1961, XXII, pp. 579ss.

Glashow, S. L., Iliopopulos, J., Maiani, L., Weak interactions with lepton-hadron symmetry, in ‟Physical review", 1970, II, pp. 1285-1292.

Goldstone, J., Salam, A., Weinberg, S., Broken symmetries, in ‟Physical review", 1962, CXXVII, pp. 965-970.

Greenberg, O. W., Spin and unitary-spin independence in a paraquark model of barions and mesons, in ‟Physical review letters", 1964, XIII, pp. 598-602.

Gross, D. J., Wilczek, F., Asymptotically free gauge theories, in ‟Physical review", 1973, VIII, pp. 3633-3652.

Gross, D. J., Wilczek, F., Ultraviolet behavior of non-abelian gauge theories, in ‟Physical review letters", 1973, XXX, pp. 1343-1346.

Gürsey, F., Radicati, L., Spin and unitary spin independence of strong interactions, in ‟Physical review letters", 1964, XIII, pp. 173-175.

Hasert, F. J. e altri, Search for elastic muon-neutrino-electron scattering, in ‟Physics letters", 1973, XLVI, pp. 121-124.

Heisenberg, W., Zur Theorie der Schauer, in der Höhenstrahlung, in ‟Zeitschrift für Physik", 1936, CI, pp. 533-540.

Heisenberg, W., Über die in der Theorie der elementarteilchen auftretende universelle Länge, in ‟Annalen der Physik", 1938, XXXII, pp. 20-33.

Higgs, P. W., Broken symmetries, massless particles and gauge fields, in ‟Physics letters", 1964, XII, pp. 132-133.

Higgs, P. W., Broken symmetries and the masses of gauge bosons, in ‟Physical review letters", 1964, XIII, pp. 508-509.

Hooft, G., 't, Renormalizable lagrangian for massive Yang-Mills fields, in ‟Nuclear physics", 1971, XXXVB, pp. 167-188.

Hooft, G., 't, Renomarlization of massless Yang-Mills fields, in ‟Nuclear physics", 1971, XXXIIIB, pp. 173-199.

Hooft, G., 't, Magnetic monopoles in unified gauge theories, in ‟Nuclear physics", 1974, LXXIX, pp. 276-284.

Hooft, G., 't, Magnetic charge quantization and fractionally charged quarks, in ‟Nuclear physics", 1976, CV, pp. 538-547.

Hooft, G., 't, Simmetry breaking through Bell-Jakiw anomalies, in ‟Physical review letters", 1976, XXXVII, pp. 8-11.

Hooft, G., 't Veltman, M., Regularization and renormalization of gauge fields, in ‟Nuclear physics", 1972, XLIV, pp. 189-213.

Johnson, K., Low, F. E., Current algebras in a simple model, in ‟Progress of theoretical physics", 1966, XXXVII-XXXVIII, pp. 74-93.

Kibble, T. W. B., Symmetry breaking in non-abelian gauge theories, in ‟Physical review", 1967, CLV, pp. 1554-1561.

Kibble, T. W. B., Topology of cosmic domains and strings, in ‟Journal of physics", 1976, IX, pp. 1387-1398.

Kobayashi, M., Maskawa, K., CP-violation in the renormalizable theory of weak interactions, in ‟Progress of theoretical physics", 1973, IL, pp. 652-657.

Kuang-chao chou, On the pseudovector current and lepton decays of baryons and mesons, in ‟Journal of experimental and theoretical physics", 1961, XII, pp. 492-497.

Lederman, L. e altri, Observation of a dimuon resonance at 9.5 Gev in 400 GeV proton-nucleus collisions, in ‟Physical review letters", 1977, XXXIX, pp. 252-255.

Lee, B. W., Renormalizable massive vector-meson theory. Perturbation theory of the Higgs phenomenon, in ‟Physical review", 1972, V, pp. 823-835.

Lee, B. W., Zinn-Justin, J., Spontaneously broken gauge symmetries I, II, III, in ‟Physical review", 1972, V, pp. 3121-3160.

Lee, B. W., Zinn-Justin, J., Spontaneously broken gauge symmetries IV, in ‟Physical review", 1973, VII, pp. 1049-1056.

Llewellyn-Smith, C., High energy behaviour and gauge symmetry, in ‟Physics lettes", 1973, XLVI, pp. 233-236.

Low, F. E., Current algebras and sum rules, in ‟Comments on nuclear and particle physics", 1968, II, pp. 15-17.

Marciano, W., Pagels, H., Quantum chromodynamics, in ‟Physical reports", 1978, XXXVI, pp. 137-276.

Marciano, W. J., Sirlin, A., Precise SU(5) predictions for sin² ϑW^exp, m_W, and m_Z, in ‟Physical review letters", 1981, XLVI, pp. 163-166.

Mueller, A., Perturbative QCD at high energies, in ‟Physical reports", 1981, LXXIII, pp. 237-368.

Parisi, G., Deep inelastic scattering in a field theory with computable large-momenta behaviour, in ‟Nuovo Cimento lett.", 1973, VII, pp. 84-88.

Perl, M. L., The tau lepton, in ‟Annual review of nuclear and particle science", 1980, XXX, p. 299 ss.

Perl, M. L. e altri, Evidence for anomalous lepton production in e⁺e^- annihilation, in ‟Physical review letters", 1975, XXXV, pp. 1489-1492.

Politzer, H. D., Reliable perturbative results for strong interactions, in ‟Physical review letters", 1973, XXX, pp. 1346-1349.

Politzer, H. D., Asymptotic freedom: an approach to strong interactions, in ‟Physical reports", 1974, XVI, pp. 129-180.

Polyakov, A. M., Particle spectrum in quantum field theory, in ‟Pis'ma Zhurnal éksperimental'noĭ i teoreticheskoĭ fiziki", 1974, XX, pp. 430-433.

Preskill, J., Cosmological production of superheavy magnetic monopole, in ‟Physical review letters", 1979, XLIII, pp. 1365-1368.

Sakharov, A. D., Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe, in ‟Pis'ma Zhurnal éksperimental'noĭ i teoreticheskoĭ fiziki", 1967, V, pp. 32-35.

Salam, A., Elementary particle theory, Proceedings of the Eight Nobel symposium, New York 1968.

Salam, A., Nonpolynomial lagrangians, renormalization and gravity, in Proceedings of the Coral Gables Conference (a cura di M. Dal Cin, G. J. Iverson e A. Perlmutter), New York 1971.

Salam, A., Ward, J. C., Electromagnetic and weak interactions, in ‟Physics letters", 1964, XIII, pp. 168-171.

Susskind, L., Dynamics of spontaneous symmetry breaking in the Weinberg-Salam theory, in ‟Physical review", 1979, XX, pp. 2619-2625.

Symanzik, K., Small-distance-behaviour in field theory and power counting, in ‟Communications in mathematical physics", 1970, XVIII, pp. 227-239.

Symanzik, K., Small-distance-behaviour analysis and Wilson expansion, in ‟Communications in mathematical physics", 1971, XXIII, pp. 49-86.

Symanzik, K., Small-distance behaviour in field theory, in ‟Springer tracts in modern physics", 1971, LVII, pp. 222-236.

Toussaint, D. e altri, Matter-antimatter accounting, thermodynamics, and black-hole radiation, in ‟Physical review", 1979, XIX, pp. 1036-1045.

Weinberg, S., A model of leptons, in ‟Physical review letters", 1967, XIX, pp. 1264-1266.

Weinberg, S., Current algebra and gauge theories. Non abelian gluons, in ‟Physical review", 1973, VIII, pp. 4482-4498.

Weinberg, S., Gauge theory of CP nonconservation, in ‟Physical review letters", 1976, XXXVII, pp. 657-661.

Weisberger, W., Renormalization of the weak axial-vector coupling constant, in ‟Physical review letters", 1965, XIV, pp. 1047-1051.

Wilson, K., Non-lagrangian models of current algebra, in ‟Physical review", 1969, CLXXIX, pp. 1499-1512.

Wu, C. S., The universal Fermi interaction and the conserved vector in β decay, in ‟Review of modern physics", 1964, XXXVI, pp. 618-632.

Yang, C.N., Mills, R. L., Conservation of isotopic spin and isotopic gauge invariance, in ‟Physical review", 1954, XCVI, pp. 191-196.

Zee, A., Electron-positron annihilation in stagnant field theories, in ‟Physical review", 1973, VIII, pp. 4038-4041.

Zee, A., Study of the renormalization group for small coupling constants, in ‟Physical review", 1973, VII, 3630-3636.

Zee, A., Grand unification and gravity, in Grand unification and related topics. Proceedings of the 1981 Kyoto summer school, Kyoto 1981.

Zimmerman, W., Problems in vector meson theories, in ‟Springer tracts in modern physics", 1969, L, pp. 143-156.