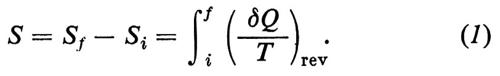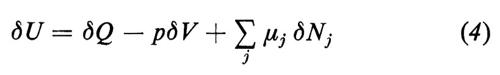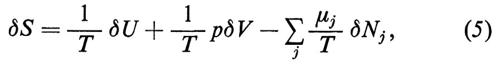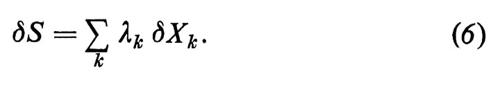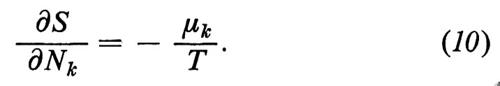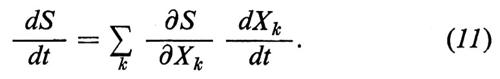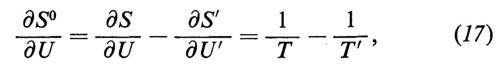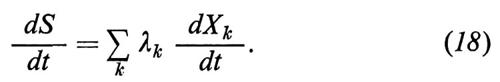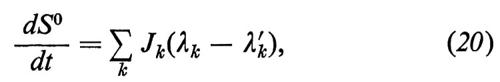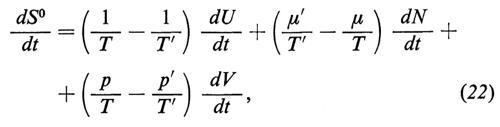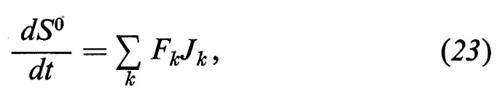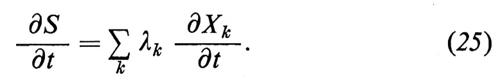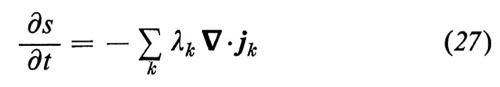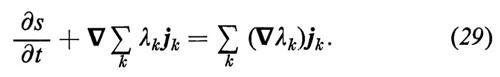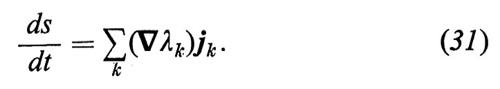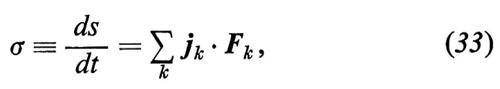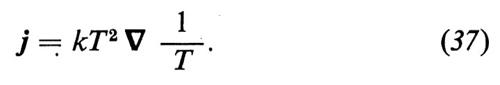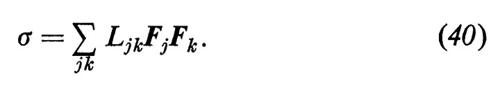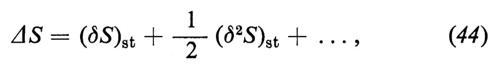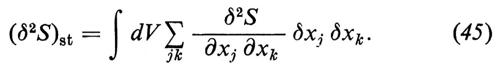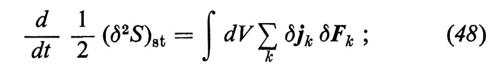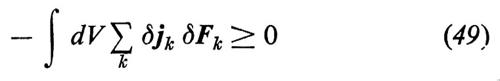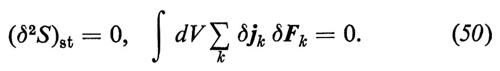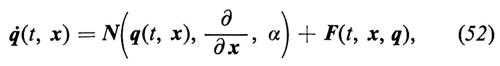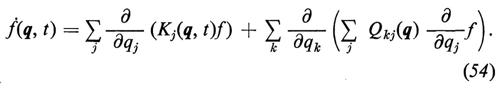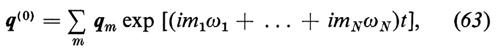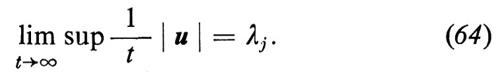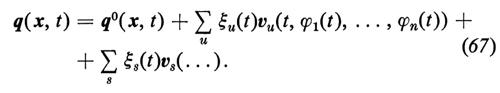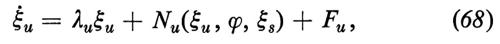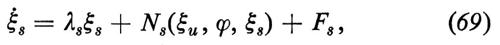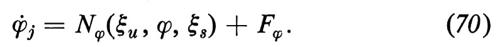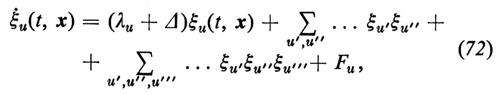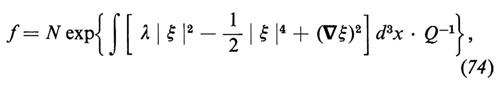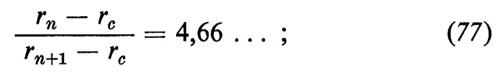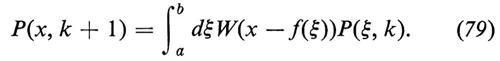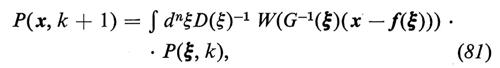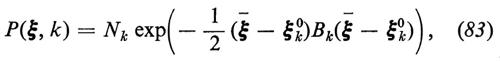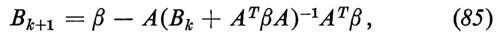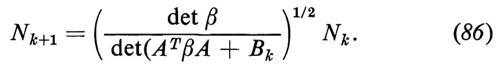Termodinamica irreversibile e sinergetica

Termodinamica irreversibile e sinergetica

di Hermann Haken

SOMMARIO: 1. Campo d'indagine della termodinamica irreversibile e della sinergetica. □ 2. Termodinamica irreversibile. Formulazione matematica. □ 3. Sinergetica: a) fenomeni tipici; b) fisica; c) ingegneria; d) chimica; e) biologia; f) scienze dei calcolatori; g) economia; h) ecologia; i) sociologia; l) caratteristiche comuni agli esempi sopra riportati. □ 4. I concetti fondamentali e gli strumenti matematici della sinergetica: a) concetti fondamentali e terminologia; b) impostazione matematica; c) costruzione di soluzioni di biforcazione per risolvere le equazioni non lineari (52); d) esempi; e) il caos. □ 5. Conclusione. □ Bibliografia.

1. Campo d'indagine della termodinamica irreversibile e della sinergetica.

La termodinamica, la termodinamica irreversibile e la sinergetica mirano a dedurre le leggi generali e i principî che regolano il comportamento macroscopico della materia a prescindere dalla natura dei suoi costituenti, atomi e molecole. Inoltre la sinergetica si occupa anche di fenomeni che esulano dal campo delle scienze naturali e rientrano in quelli dell'economia, dell'ecologia e della sociologia.

I concetti fondamentali della termodinamica sono la temperatura e il calore, per mezzo dei quali si può definire l'entropia (v. sotto). La prima legge della termodinamica esprime la conservazione dell'energia. L'energia, mentre può trasformarsi da una forma in un'altra (per esempio da meccanica in calore), non può, in un sistema chiuso, essere generata o annichilata in assoluto.

La seconda legge della termodinamica riguarda la direzione secondo cui possono svolgersi i processi di trasformazione di certi tipi di energia. In base a questa legge non si può costruire una macchina che lavori eseguendo cicli periodici il cui unico risultato sia la trasformazione di calore in energia meccanica (o d'altro tipo).

Nella sua formulazione generale, la seconda legge afferma che, se un sistema macroscopico, che non può scambiare calore con l'esterno, compie una trasformazione termodinamica, esiste una funzione delle variabili che ne definiscono lo stato termodinamico, la quale nella trasformazione non può decrescere e, quindi, raggiunge il valore massimo, fra quelli compatibili con i vincoli, in corrispondenza dello stato di equilibrio del sistema. Questa funzione è l'‛entropia', S, che fu introdotta, come concetto essenziale della termodinamica, da R. J. E. Clausius nel secolo scorso. La variazione di entropia S_f − S_i di un sistema, che subisca una trasformazione da uno stato iniziale i a uno stato finale f, è data dall'integrale, calcolato lungo una qualunque trasformazione ‛reversibile', del differenziale δQ/T, dove Q è il calore trasmesso al sistema alla temperatura T:

Su scala microscopica, dove le leggi fenomenologiche della termodinamica si deducono applicando la meccanica statistica ai componenti microscopici della materia, riveste un ruolo essenziale la concezione dell'entropia dovuta a L. Boltzmann (v., 1896-1898). Secondo questa concezione, se uno stesso stato macroscopico di un sistema può essere realizzato da W stati microscopici diversi, l'entropia del sistema è

S = k In W, (2)

dove k è una costante. La fig. 1 fornisce una visualizzazione del concetto di entropia di Boltzmann.

Le variazioni dell'entropia e i flussi che le determinano sono fondamentali anche nella termodinamica irreversibile e nella sinergetica, perché consentono di definire nella maggioranza dei casi il grado di irreversibilità delle trasformazioni subite dai sistemi macroscopici. Nell'ambito della termodinamica irreversibile (v. Boltzmann, 1896-1898; v. Thomson, 1854) si tenta di generalizzare i risultati della termodinamica classica a sistemi macroscopici che si discostino alquanto dall'equilibrio termico. In primo luogo si considerano quindi i fenomeni di trasporto e di rilassamento (v. figg. 2 e 3). Un esempio è dato dalla corrente elettrica, cioè dal fluire di cariche elettriche, come quelle degli elettroni, in un conduttore metallico. Per attrito interno, parte dell'energia cinetica degli elettroni si trasforma in calore; il processo è irreversibile, perché il fenomeno inverso non si verifica in natura: infatti non è possibile produrre una corrente elettrica riscaldando omogeneamente un conduttore. Nel corso di questi processi si produce entropia.

Concetti fondamentali della termodinamica irreversibile sono i ‛flussi' (per es. la corrente elettrica, la corrente di calore, la diffusione, ecc.), le ‛forze' (per es. le differenze di potenziale elettrico, di temperatura, di concentrazione di particelle, ecc.) e la ‛produzione di entropia'.

La sinergetica, invece, considera sistemi fisici, chimici e biologici lontani dall'equilibrio termico e cosi studia anche il verificarsi di fenomeni qualitativamente nuovi, che non possono aver luogo in sistemi che siano in equilibrio o prossimi all'equilibrio. Questi nuovi fenomeni comprendono oscillazioni (‛ritmi') di stati elettrici, chimici e biologici e formazioni di strutture (‛morfogenesi'). Numerosi esempi di questi processi saranno presentati nel cap. 3. Inoltre la sinergetica studia anche la formazione di strutture e di configurazioni in sistemi sociali, economici, ecologici, ecc.; ma, analogamente alla termodinamica e alla termodinamica irreversibile, anche la sinergetica punta alla scoperta e alla formulazione di leggi generali indipendenti dalla natura degli elementi che costituiscono i sistemi in esame.

2. Termodinamica irreversibile. Formulazione matematica.

La termodinamica irreversibile si basa sugli stessi concetti fondamentali di temperatura, T, e di quantità di calore, Q, che sono propri della termodinamica elementare. Assumere una temperatura definita significa postulare che il sistema in esame sia in equilibrio termico. Se un tale sistema è in contatto con l'ambiente che lo circonda, la sua entropia S può cambiare di una quantità

dove δQ è la quantità di calore scambiata reversibilmente.

Per la prima legge della termodinamica, che stabilisce la conservazione dell'energia in un sistema isolato, si può esprimere δQ tramite la variazione δU dell'energia interna, il lavoro pδV (p = pressione, V = volume) e le variazioni di energia dovute agli scambi di particelle. Distinguendo con l'indice j i numeri N_j di particelle di specie diverse, la variazione dell'energia dovuta alle reazioni che cambiano i valori di N_j è data dalla somma Σ_j δN_jμ_j, dove i μ_j sono i potenziali chimici. Pertanto è

e dalla (3) si ottiene la relazione di Gibbs

che può essere posta nella forma generale

Se si varia una sola delle variabili di S, lasciando le altre inalterate, si ha

e dalla (5) seguono in particolare le relazioni

Nel seguito studieremo processi nei quali gli X_k variano nel tempo t. Conseguentemente anche S dipende dal tempo ed è

Passiamo ora ad esporre la termodinamica irreversibile.

Si consideri un sistema suddiviso in singoli elementi di volume in ognuno dei quali esista un equilibrio termico locale tale da consentirci di definire, in particolare, una temperatura e un'entropia locali. Si assuma inoltre che gli elementi di volume siano accoppiati in modo che fra di essi possa avvenire uno scambio di energia e/o di materia. Date queste condizioni, l'entropia S del sistema è una funzione dello spazio x e del tempo t:

S = S(x, t). (12)

Volendo studiare in qual modo l'entropia vari per scambi di energia e di materia, si postula che essa sia una grandezza estensiva, cioè una grandezza definita in generale come segue. Supponendo, per semplicità, che il volume V sia suddiviso in due parti, V₁ e V₂, cioè che sia

V₁ + V₂ = V, (13)

per una variabile estensiva X, connessa a ognuna di esse, vale la relazione

X_V1 + X_V2 = X_V (14)

o semplicemente

X + X′ = X⁰, (15)

avendo posto X_V1 = X, X_V2 = X′ e X_V = X⁰. In particolare, essendo l'entropia una variabile estensiva, si ha

S + S′ = S⁰ (16)

Si tratta ora di vedere come vari l'entropia S⁰ quando cambia una delle variabili da cui dipende. Per esempio, se la variabile X è l'energia interna U, per la (8), si ha

avendo assunto δU⁰ = δU + δU′ = 0, cioè che il sistema sia isolato. In generale, per la (11) e la (7), le variazioni temporali di S sono date dalla

La derivata rispetto al tempo di una variabile estensiva X_k,

si chiama ‛flusso' di X_k. Per la (16) e la (18) si ha

essendo la somma estesa a tutte le variabili estensive da cui dipende S⁰. Le differenze

(λ_k − λ′_k) = F_k (21)

si chiamano ‛forze termodinamiche generalizzate' o ‛affinità'. Per esempio, per una trasformazione generica, limitandosi, per semplicità, a una sola specie di particelle, si ottiene

avendo tenuto conto delle (8), (9) e (10). Questa equazione esprime come l'entropia di tutto il sistema cambi se i due elementi di volume hanno temperature, pressioni e potenziali chimici diversi. Le grandezze dU/dt, ecc. devono essere determinate tramite altre relazioni (v. sotto).

Usando la (21) si può porre la (20) nella forma

che definisce la ‛produzione di entropia'. Questa relazione e altre ad essa connesse possono essere derivate facilmente anche per mezzi i cui parametri di stato varino con continuità. Indicando con ΔS l'entropia di un elemento di volume ΔV, la ‛densità di entropia', nel limite in cui ΔV sia sufficientemente piccolo, è definita dal rapporto

Denotiamo ancora con X_k le variabili estensive relative all'elemento di volume ΔV.

Onde derivare un'equazione di continuità per la densità di entropia, consideriamo come essa vari localmente nel corso del tempo; consideriamo cioè la derivata

Assumiamo ora che le quantità estensive X_k soddisfino un'equazione di continuità,

Ú_k + ∇ • j_k = 0, (26)

che sostituisce la (19). La (26) rappresenta una legge di conservazione per l'energia, per il numero di particelle o per altre grandezze. Per mezzo della (26), la (25) si trasforma nella seguente:

e poiché si ha

λ_{k ∇} • j_k = ∇(λ_k j_k) − j_{k ∇}λ_k, (28)

si può infine scrivere la (27) nella forma

Nella (29) l'espressione a primo membro ha la tipica forma di un'equazione di continuità. Da ciò deriva l'idea di interpretare la grandezza

come ‛flusso di entropia'. L'espressione a secondo membro della (29) si può interpretare come ‛intensità di produzione locale di entropia'. Si può cioè scrivere

Ponendo

∇λ_k = F_k, (32)

possiamo riscrivere la (31) come segue:

dove le F_k indicano le forze termodinamiche generalizzate.

Per poter ricavare dalla (33) o dalla (31) la produzione di entropia, si devono conoscere i flussi, il che richiede l'assunzione di ipotesi supplementari.

Le ipotesi consuete nella termodinamica irreversibile sono: a) i flussi a un istante determinato dipendono solo dalle affinità (o forze termodinamiche generalizzate) agenti in quell'istante; b) i processi sono lineari, nel qual caso i flussi sono proporzionali alle forze:

i coefficienti L_kj si chiamano ‛coefficienti di Onsager'. In prossimità dell'equilibrio termico vale la ‛relazione di reciprocità di Onsager'

L_kj = L_jk, (35)

enunciata come teorema di Onsager nel modo seguente: in prossimità dell'equilibrio termico la j-esima affinità produce nel k-esimo flusso un effetto lineare simmetrico a quello prodotto dalla k-esima affinità nel flusso j-esimo (v. Onsager, 1931). La (35) può essere dimostrata quando si assuma la reversibilità microscopica.

Un semplice esempio che illustra la relazione (34) è rappresentato dal flusso di calore j. Fenomenologicamente esso è connesso al gradiente della temperatura T dalla relazione

j = − k∇T, (36)

dove k è il coefficiente di conducibilità. La (36) si può scrivere anche come segue:

Confrontando la (37) con la (32) e con la (34), si può identificare

con l'affinità e

kT² (39)

con il coefficiente cinetico L₁₁.

Altri esempi sono forniti dalla legge di Ohm per la conduzione elettrica o dalla legge di Fick per la diffusione. Comunque, secondo la (34), si hanno diverse relazioni accoppiate fra vari processi di trasporto con coefficienti simmetrici in accordo con la (35). Inserendo la (34) nella (33) possiamo, d'altra parte, esprimere la produzione di entropia nella forma

La produzione totale di entropia di un sistema si ottiene integrando σ sull'intero volume:

P = ∫ σ dV. (41)

Alcune scuole di termodinamica irreversibile (v. Prigogine, 1947) hanno cercato di usare la produzione di entropia come criterio per decidere in quale direzione evolva un processo. Secondo il ‛principio della produzione minima di entropia', vale la diseguaglianza

dove il segno di uguaglianza corrisponde a uno stato stazionario. Quindi, per questo principio, negli stati stazionari la produzione di entropia deve essere minima. Tuttavia è da notare che questo principio è valido solo per una classe di sistemi puramente dissipativi nel dominio lineare molto prossimo all'equilibrio termico. Infatti esso proibirebbe anche oscillazioni temporali smorzate delle variabili di stato vicino all'equillibrio. Esempi che contraddicono il principio della produzione minima di entropia sono forniti dai circuiti elettrici con capacità e induttanze (v. i contributi di Landauer, 1975).

Un altro criterio evolutivo spesso discusso nella letteratura è quello detto dell'‛eccesso di produzione di entropia'. Consideriamo l'eccesso di entropia ΔS intorno a uno stato stazionario ‛di riferimento',

ΔS = S(x) − S(x_st), (43)

dove x e x_st sono parametri di stato rispettivamente dello stato in esame e dello stato di riferimento. Sviluppando la (43) intorno allo stato di riferimento, si ha

dove, in particolare, si può scrivere

Se lo stato di riferimento è uno stato di equilibrio, allora si ha

(δ²S)_st ≡ (δ²S)_eq ≤ 0. (46)

Si assume che questa relazione si possa estendere agli stati di non equilibrio, purché sussista l'equilibrio locale e quindi si abbia

(δ²S)_st ≤ 0. (47)

La derivata rispetto al tempo della (45) si può, dopo alcuni passaggi, mettere nella forma

l'integrale a secondo membro della (48) è chiamato ‛eccesso di produzione di entropia'. Corrispondentemente si afferma ('principio dell'eccesso di produzione di entropia': v. Glansdorff e Prigogine, 1971) che lo stato di riferimento è stabile se la (47) e la

valgono contemporaneamente. La (49) è una condizione sufficiente per la stabilità. La sua violazione è una condizione necessaria, ma non sufficiente, perché il sistema si discosti dallo stato di riferimento evolvendo verso regimi anche qualitativamente diversi. Se un sistema è soggetto a condizioni esterne ('controlli') diverse, S può considerarsi funzione di x e di tali condizioni. In questo caso ΔS e le grandezze che ne derivano descrivono come lo stesso ΔS e le altre grandezze varino al mutare dei controlli. Alle soglie del nuovo regime si prevede che le espressioni a primo membro della (47) e della (49) siano nulle, cioè sia

Mentre esistono casi in cui questo principio è applicabile, ve ne sono altri in cui non lo è. In particolare esso non fornisce informazioni su quanto possa accadere quando il sistema in esame si trova al punto di instabilità e oltre. In questi casi sono necessari metodi più potenti, appunto quelli forniti dalla sinergetica.

3. Sinergetica.

La sinergetica si occupa di sistemi composti da molti sottosistemi. Questi possono essere di natura molto diversa, come atomi, molecole, cellule, fotoni, organi, animali, o anche esseri umani. La sinergetica studia come la cooperazione di questi sottosistemi susciti strutture spaziali, temporali o funzionali su scala macroscopica, al cui livello queste strutture assumono proprietà che non sono presenti al livello dei sottosistemi. La sinergetica studia in particolare le situazioni nelle quali quelle strutture si manifestano in una forma autoorganizzata e cerca di scoprire i principî che governano questi processi di autoorganizzazione, indipendentemente dalla natura dei sottosistemi.

In quel che segue sono dapprima presentati alcuni fenomeni tipici del campo d'indagine della sinergetica, e poi delineati i concetti fondamentali e l'impostazione matematica della teoria.

a) Fenomeni tipici.

In questo capitolo sono presentati esempi tipici di transizioni disordine-ordine o ordine-ordine, in vari campi, dalla fisica alla sociologia. In teoria tutte le transizioni di fase di sistemi in equilibrio termico, come la transizione liquido-gas, la transizione ferromagnetica o l'instaurarsi della superconduttività, rientrano nella definizione generale dei processi studiati dalla sinergetica. D'altra parte questi fenomeni sono trattati approfonditamente dalla teoria delle transizioni di fase, in particolare, attualmente, mediante la tecnica del gruppo di rinormalizzazione. Perciò nella presente esposizione questi fenomeni non saranno trattati, mentre ci occuperemo di quei moderni sviluppi della sinergetica che la teoria delle transizioni di fase non considera.

b) Fisica.

Fluidi. - Si consideri uno strato fluido, soggetto alla gravità, contenuto in un recipiente di forma determinata, per esempio cilindrica o rettangolare.

Quando il fluido è riscaldato dal basso e la sua superficie superiore è mantenuta a una certa temperatura costante, nel liquido si stabilisce una differenza di temperatura. A causa di questa differenza di temperatura (gradiente di temperatura) si viene a creare un flusso di calore verticale. Se il gradiente di temperatura è piccolo, il trasporto di calore avviene a livello microscopico e nel fluido non è visibile alcun movimento macroscopico (v. fig. 4). Aumentando progressivamente il gradiente di temperatura, si giunge a un punto in cui, improvvisamente, in corrispondenza del cosiddetto ‛gradiente di temperatura critico', nel fluido si determina un movimento macroscopico (v. fig. 5): il liquido, trasportato verso l'alto da correnti ascensionali, giunto in superficie si raffredda e riscende seguendo analoghe correnti dirette verso il basso. Si instaura così un movimento circolare; il diametro dei cilindri formati dalle correnti convettive è dell'ordine dello spessore dello strato di fluido e in laboratorio può andare da alcuni millimetri a parecchi centimetri. Lo stesso fenomeno, con dimensioni di alcune centinaia di metri, si osserva in meteorologia (v. fig. 6).

Se in un recipiente rettangolare il gradiente di temperatura, che in unità adimensionali si misura mediante il numero di Rayleigh, è ulteriormente aumentato, i cilindri di corrente cominciano a oscillare e, per valori ancora più alti del numero di Rayleigh, si instaura un moto oscillatorio con parecchie frequenze. Infine compare un moto del tutto irregolare, detto ‛turbolenza' o ‛caos'.

Vi sono anche altri modi di evoluzione da uno strato quiescente alla turbolenza. Uno di questi è determinato dal cosiddetto ‛raddoppio di periodo': all'aumentare del numero di Rayleigh, si manifesta un movimento complesso, tale che, per ben definiti numeri di Rayleigh successivi, il valore del periodo del moto diventa ogni volta il doppio del precedente (v. fig. 7).

In recipienti cilindrici si possono osservare moti circolari concentrici oppure, se manca la simmetria rispetto al piano mediano orizzontale, configurazioni esagonali (v. flg. 8). Si verificano anche transizioni fra moti circolari ed esagonali e persino la coesistenza di questi due tipi di moti (v. fig. 9). Altre configurazioni possibili sono cerchi che tendono a disporsi in forme rettangolari e che quindi vengono a costituire un reticolo rettangolare (v. fig. 10).

Per numeri di Rayleigh elevati si forma una struttura a tappeto (v. fig. 11) con oscillazioni radiali. Molte configurazioni possono presentare anche un certo numero di imperfezioni (v. fig. 12).

Le instabilità appena descritte si chiamano instabilità di Bénard o ‛di convezione'.

Per ottenere risultati più chiaramente definiti, nei moderni esperimenti si sceglie un ‛rapporto di formato' (rapporto fra la dimensione orizzontale e quella verticale del recipiente) piccolo, cioè dell'ordine dell'unità. Per rapporti di formato più elevati le singole transizioni possono susseguirsi molto rapidamente o persino coesistere.

Fenomeni analoghi sono associati all'instabilità di Taylor. In questo caso si studia il moto di un liquido contenuto fra due cilindri coassiali, di cui quello interno ruota. Per basse velocità di rotazione, nel liquido si formano linee di corrente coassiali; al di là di una velocità di rotazione critica (misurata in numeri di Taylor, adimensionali), si instaura un moto ‛a cilindri', in cui il campo di velocità del liquido ha delle componenti orizzontali (v. fig. 13A). All'aumentare del numero di Taylor, i cilindri incominciano a oscillare con una (v. fig. 13B) o due (v. fig. 13C) frequenze fondamentali; talvolta si hanno schemi di frequenza ancora più complicati. Infine si instaura un moto turbolento (caotico) (v. fig. 13D).

In meteorologia e in astrofisica (per es. nello studio delle atmosfere dei pianeti) si incontrano ulteriori esempi di instabilità e di formazioni di configurazioni.

Laser. - I laser sono sorgenti luminose capaci di emettere luce coerente. Il termine ‛laser' è l'acronimo dell'espressione Light Amplification by Stimulated Emission of Radiation.

Nel laser, in genere, la luce è non soltanto amplificata, ma anche generata coerentemente. Un laser (v. fig. 14) è costituito da un materiale laser attivo, che può essere un cristallo di rubino, atomi di gas o molecole di colorante in soluzione; di solito ai due estremi del tubo che contiene il materiale attivo sono montati due specchi, che conferiscono un'elevata persistenza alle onde luminose emesse in direzione assiale (v. fig. 15) e selezionano le lunghezze d'onda in modo che siano emesse solo onde stazionarie con lunghezze d'onda discrete. Gli atomi laser attivi sono eccitati dall'esterno, per es. da un'intensa sorgente luminosa o da una scarica in un gas. Quando l'input di energia (o più precisamente di ‛potenza') è piccolo, il laser si comporta come una lampada comune (v. fig. 16A): esso emette singoli treni d'onda di luce. Questi treni d'onda derivano dalla ricombinazione casuale degli elettroni dei singoli atomi eccitati del materiale laser. In corrispondenza di un valore critico di questo input (‛intensità di pompaggio') i treni d'onda casuali vengono rimpiazzati da un'onda sinusoidale coerente di lunghezza quasi infinita (v. fig. 16B). Ciò indica che lo stato atomico interno del laser ha subito un drastico mutamento.

Incrementando ulteriormente l'intensità di pompaggio, in corrispondenza di un altro valore critico, l'emissione coerente può essere sostituita dall'emissione di impulsi laser ultracorti. Secondo la teoria, in determinate circostanze si può avere anche emissione di luce ‛caotica', cioè con ampiezze irregolari.

In una cavità ottica e all'interno della corrispondente larghezza di riga della transizione ottica possono essere presenti diversi modi (cioè onde con differenti lunghezze d'onda o differenti direzioni di propagazione). Lo studio della compatibilità di questi modi durante il funzionamento del laser è un problema molto importante. Se la riga è allargata in modo omogeneo e si usa una cavità ad anello, sopravvive un solo modo, tutti gli altri vengono eliminati. Invece in una cavità con onde stazionarie, per effetto di varie interazioni locali delle onde con gli atomi laser (il cosiddetto ‛spatial hole burning'), possono coesistere diversi modi. Analogamente, in una riga di larghezza non omogenea possono coesistere parecchi modi purché la loro distanza spettroscopica sia maggiore della larghezza omogenea della riga. Quando la coesistenza dei modi è possibile può verificarsi un agganciamento di frequenza, cioè diversi modi incominciano a oscillare in fase con intervalli di frequenza fissati. Se un laser è soggetto a un campo elettromagnetico esterno in risonanza o prossimo alla risonanza con la transizione ottica atomica, si può ottenere la bistabilità ottica, cioè il laser può funzionare in uno qualunque di due stati stabili. Un tale dispositivo può essere impiegato come elemento di logica o di memoria.

Per maggiori dettagli sulla fisica del laser v. ottica quantistica.

Plasmi. - Un plasma è un gas di atomi parzialmente o totalmente privati della loro nube elettronica, cioè di atomi ionizzati. In un plasma si osserva una grande varietà di instabilità, che in questo articolo non è il caso di elencare. In particolare, al variare delle condizioni del pompaggio esterno, non solo si raggiungono nuovi stati ordinati, ma il plasma può anche migrare da un'instabilità a un'altra o può subire un'instabilità violenta per cui uno stato di plasma collassa. La fig. 17 mostra un risultato teorico.

Fisica dello stato solido. - Diamo alcuni esempi di sistemi ove, al mutare delle condizioni esterne, si instaurano fenomeni qualitativamente nuovi.

1. L'oscillatore di Gunn. Se si applica una differenza di potenziale relativamente modesta a un campione di arseniuro di gallio (GaAs), vi si genera una corrente costante che obbedisce alla legge di Ohm. All'aumentare della differenza di potenziale, in corrispondenza di un suo valore critico, alla corrente costante si sostituiscono degli impulsi regolari. Con differenze di potenziale ancora più elevate si possono osservare anche impulsi irregolari (caos). Le correnti a impulsi brevi nella regione delle microonde si generano in quanto il GaAs ha diverse bande di conduzione e gli elettroni passano, per effetto tunnel, dalla banda di conduzione più bassa alla più alta quando l'intensità del campo cresce.

2. I diodi tunnel sono costituiti da semiconduttori drogati con ben definite impurità atomiche, in modo che le bande di energia (in particolare la banda di valenza e quella di conduzione) siano deformate (v. fig. 18). Quando si applica un campo elettrico al diodo, si genera una corrente tunnel e si possono ottenere diversi stati operativi del diodo tunnel (v. fig. 19).

3. Drastici mutamenti qualitativi su scala macroscopica si possono osservare anche in meccanica, per esempio nel caso di instabilità termoelastiche. Quando si deforma un solido oltre i limiti di elasticità, in corrispondenza di valori critici degli sforzi applicati, si possono verificare fenomeni qualitativamente nuovi, per esempio emissioni acustiche e altri fenomeni.

c) Ingegneria.

Ingegneria meccanica. - In ingegneria meccanica sono ben noti casi di sistemi che subiscono drastici mutamenti a livello macroscopico, in seguito al cambiamento dei parametri di controllo esterni. Ecco alcuni esempi: il flettersi di una sbarra sotto un peso, fenomeno trattato da Eulero (v. fig. 20); il crollo di un ponte soggetto a un carico eccedente un certo valore critico; le deformazioni di un guscio sottile, sottoposto a un carico omogeneo (v. fig. 21); in quest'ultimo caso si possono osservare configurazioni a esagoni o altri schemi di deformazione. Le instabilità meccaniche possono anche aver luogo in maniera dinamica: è questo il caso delle vibrazioni delle ali degli aerei.

Ingegneria elettronica. - Il presentarsi di oscillazioni elettriche o elettromagnetiche generate da oscillatori elettromagnetici autosostenentisi può anche essere visto come un modo di autoorganizzarsi del moto degli elettroni. Mentre in assenza di oscillazioni gli elettroni si muovono casualmente, essendo il loro moto connesso al rumore termico, date opportune condizioni esterne, si possono mantenere delle oscillazioni di correnti elettriche macroscopiche che percorrono il circuito elettronico. Nel caso di oscillatori accoppiati, si verificano vari fenomeni del tipo di quelli che abbiamo incontrato a proposito della fluidodinamica: aggancio delle frequenze, o caos, cioè emissione irregolare.

Di grande importanza è la questione se un sistema di oscillatori accoppiati possa ancora comportarsi come un insieme di oscillatori con frequenze individuali definite, o se in tal caso si presentino tipi di moto del tutto nuovi, per esempio un regime caotico (v. cap. 4).

d) Chimica.

Per quanto riguarda la chimica, la sinergetica si occupa di quei fenomeni in cui si manifestano configurazioni macroscopiche. Generalmente, quando determinati reagenti sono portati a contatto e ben rimescolati, ne deriva un prodotto finale omogeneo. Tuttavia, un certo numero di reazioni può presentare strutture temporali o spaziali o spazio-temporali; l'esempio più noto di questo tipo di reazioni è la reazione di Belousov-Chabotinsky, ottenuta mettendo insieme e rimescolando Ce₂(SO₄), KBrO₃, CH₂(COOH)₂ e H₂SO₄, con l'aggiunta di alcune gocce di ferroina (indicatore redox). Il preparato, messo in un reattore a vasca chiusa tenuto in continuo movimento, può presentare oscillazioni di composizione, come si può constatare osservando direttamente il mutamento di colore della composizione stessa, che passa periodicamente dal rosso al blu (v. fig. 22). In un sistema chiuso, cioè senza l'aggiunta di nuovi reagenti, queste oscillazioni finiscono per scomparire. D'altra parte, se si aggiungono continuamente nuovi reagenti e, contemporaneamente, si rimuovono i prodotti finali, le oscillazioni si possono mantenere indefinitamente. Oggigiorno si conoscono più di una dozzina di sistemi che mostrano oscillazioni chimiche. Variando la concentrazione iniziale di un reagente, si può dar luogo a tutta una serie di diversi tipi di comportamento, per esempio a un'alternanza di oscillazioni e di comportamenti caotici (v. fig. 23). Se le sostanze chimiche non vengono mescolate, possono svilupparsi configurazioni spaziali. La reazione di Belousov-Chabotinsky offre esempi di simili configurazioni nella forma di onde concentriche (v. fig. 24) o di spirali (v. fig. 25). Alcune reazioni oscillanti possono essere influenzate dalla luce (fotochimica), che può indurre o stati caotici o aggancio delle frequenze. Si prevede che i metodi e i concetti della sinergetica (v. sotto) potranno essere applicati alla chimica anche a livello molecolare, in particolare per lo studio del comportamento delle molecole biologiche. Ma queste applicazioni sono ancora in corso di sviluppo, per cui sarebbe prematuro parlarne in questa sede.

e) Biologia.

Morfogenesi. - Il problema centrale della morfogenesi è come facciano cellule inizialmente indifferenziate a sapere dove e in qual modo differenziarsi. Gli esperimenti indicano che questa informazione non è in possesso delle singole cellule fin dall'inizio, ma che una cellula appartenente a un tessuto riceve dall'ambiente circostante informazioni sulla sua posizione, in base alle quali poi si differenzia. Per esempio, se si trapianta una parte della testa di Hydra in un'altra regione del corpo, in questa regione si sviluppa una nuova testa, purché il luogo del trapianto sia abbastanza lontano dalla posizione originaria della testa; infatti, se il frammento di testa viene trapiantato in una zona troppo vicina a quella di origine, la testa non si riforma (per altri esperimenti v. fig. 26). In altri esperimenti su embrioni, il trapianto di una cellula da una regione centrale del corpo nella regione della testa fa sì che la cellula trapiantata si trasformi in una cellula dell'occhio. Questi esperimenti dimostrano che le cellule non ricevono l'informazione su come svilupparsi fin dall'inizio (per es. dal DNA), ma la ricevono in base alla posizione che occupano nel tessuto cui appartengono. Si suppone che l'informazione ‛posizionale' sia fornita da una ‛preconfigurazione' chimica che evolve come le configurazioni descritte nel paragrafo d. Queste formazioni di configurazioni si basano sulla cooperazione di reazioni e diffusione di molecole. In Hydra sono state trovate alcune sostanze chimiche che presumibilmente rivestono il ruolo di molecole che promuovono o inibiscono la formazione di teste o piedi. Il ruolo delle sostanze chimiche nella formazione di configurazioni risulta evidente nel processo di sviluppo di un piccolissimo fungo, il fungo mucoso (v. fig. 27). Di solito le cellule di questo fungo vivono separate le une dalle altre su un substrato; ma quando il nutrimento comincia a scarseggiare le cellule si aggregano, si differenziano e formano il fungo. Il processo di aggregazione è governato dall'emissione spontanea e rinforzata di adenosinmonofostato ciclico (cAMP). Attraverso l'interazione di produzione e diffusione di queste molecole sul substrato, si possono formare onde a spirale (v. fig. 28). Le singole cellule sono capaci di misurare il gradiente di concentrazione verso cui si muovono per mezzo di piccoli pseudopodi. Il cAMP interviene anche nei successivi processi di differenziazione delle cellule, ma il meccanismo in gioco non è ancora noto nei dettagli.

Dinamica delle popolazioni. - In questo settore i fenomeni da spiegare sono, fra gli altri, quelli dell'abbondanza e della distribuzione delle specie. Specie differenti che si nutrano esclusivamente dello stesso cibo entrano in competizione; in questo caso si applica la legge darwiniana della sopravvivenza del più idoneo (esiste una stretta analogia fra questo fenomeno e la competizione fra i modi di un laser). Se sono disponibili diverse risorse alimentari, allora diventa possibile la coesistenza di specie differenti.

Le specie possono mostrare oscillazioni temporali. All'inizio di questo secolo i pescatori dell'Adriatico notarono un mutamento periodico del numero di individui di certe popolazioni ittiche.

Queste oscillazioni dipendono dall'‛interazione' fra predatori e prede. Se i predatori mangiano troppe prede, il numero delle prede diminuisce e di conseguenza finisce per diminuire anche il numero dei predatori; questo fatto, a sua volta, favorisce un nuovo aumento del numero delle prede, che comporta un aumento conseguente del numero dei predatori; si determina così una variazione ciclica della popolazione. Analoghi mutamenti periodici interessano le popolazioni di lepri delle nevi e di linci canadesi (v. fig. 29). Altre popolazioni, come certe popolazioni di insetti, possono mostrare fluttuazioni caotiche del numero di individui che le compongono.

Evoluzione. - L'evoluzione può essere riguardata come un processo, più volte ripetuto, di formazione di nuove configurazioni macroscopiche (nuovi tipi di specie). I modelli dell'evoluzione delle biomolecole si basano su una formulazione matematica del principio darwiniano della sopravvivenza del più idoneo. Si postula che le biomolecole si moltiplichino per autocatalisi (o, in maniera più complessa, per catalisi ciclica entro ‛ipercicli': v. fig. 30). Si può mostrare che questo meccanismo produce selezioni, che, combinandosi con mutazioni, possono portare a un processo evolutivo.

Sistema immunitario. - Ulteriori esempi del comportamento di complessi sistemi biologici sono forniti dalla cinetica degli enzimi e da quella anticorpi-antigeni. Per esempio, nuovi tipi di anticorpi possono formarsi in conseguenza del fatto che alcuni anticorpi si comportano come antigeni; ciò conduce a una dinamica molto complessa dell'intero sistema.

f) Scienze dei calcolatori.

Riconoscimento di configurazioni da parte di macchine. - Il riconoscimento di configurazioni è un tipico processo sinergetico. Generalmente la configurazione da individuare è scomposta nei suoi elementi (primitives) (v. fig. 31). Nel riconoscimento digitale di configurazioni, a ogni elemento è associato un certo numero che definisce un punto in uno spazio pluridimensionale (v. fig. 32). Riconoscere una configurazione significa identificare, in questo spazio pluridimensionale, i punti che corrispondono a un ‛punto ideale' (che rappresenta la configurazione prototipo) posto a distanza minima dal punto osservato (v. fig. 33). Numerosi metodi sinergetici (v. sotto) possono essere applicati a questo problema.

Autoorganizzazione di calcolatori con particolare riguardo al calcolo in parallelo. - In questo caso il problema è quello di realizzare una rete di calcolatori in cui i sottoprogrammi che costituiscono un procedimento di calcolo siano distribuiti fra i singoli componenti della rete in maniera automatica (v. fig. 34), anziché tramite l'intervento di un calcolatore pilota (v. fig. 35). La distribuzione di compiti corrisponde a certe configurazioni del flusso di informazìone. Mentre i metodi della sinergetica bastano per trattare variazioni continue del processo di elaborazione globale, resta da effettuare ancora molta ricerca prima di poter risolvere il problema di come la rete di calcolatori possa affrontare compiti qualitativamente nuovi.

Affidabilità di sistemi composti da elementi non affidabili. - In genere i singoli elementi di un sistema, specialmente a livello molecolare, possono non essere affidabili a causa di imperfezioni, fluttuazioni termiche e altri fattori. Si sospetta che gli elementi del nostro cervello, i neuroni, siano di questo tipo. La Natura, tuttavia, ha imparato a costruire sistemi affidabili a partire da elementi non affidabili.

A mano a mano che le dimensioni dei componenti dei calcolatori diminuiscono, anche la loro affidabilità va diminuendo. Sorge allora il problema di come mettere insieme questi componenti in modo che il sistema totale operi in maniera affidabile. I metodi della sinergetica (v. sotto) permettono di escogitare sistemi di tal fatta.

Passiamo ora a presentare fenomeni studiati da discipline che esulano dal campo delle scienze naturali.

g) Economia.

In economia si assiste a mutamenti macroscopici drammatici. Un tipico esempio è il passaggio da una situazione di piena occupazione a una situazione di sottooccupazione. Un mutamento di certi parametri di controllo, come il tipo di investimenti - per esempio il passaggio a investimenti per la razionalizzazione della produzione anziché per il suo incremento -, può portare a un nuovo tipo di situazione economica, per esempio a uno stato di sottooccupazione. Sono anche state osservate oscillazioni fra questi due stati, oscillazioni spiegabili con i metodi della sinergetica. Un altro esempio di sviluppo di strutture macroscopiche è il passaggio da una società agricola a una società altamente industrializzata.

h) Ecologia.

Nell'ambito dell'ecologia, e discipline affini, si può assistere a drastici cambiamenti su scala macroscopica. Per esempio, nelle regioni montane, la variazione del clima con l'altitudine, fungendo da parametro di controllo, può dar origine a diverse fasce di vegetazione. Analoghe osservazioni valgono a proposito di diverse zone climatiche terrestri, che danno origine a diversi tipi di vegetazione. Altri esempi di mutamenti macroscopici sono forniti dal fenomeno dell'inquinamento: basta che il tasso di inquinamento aumenti anche di una piccolissima frazione perché si determini la scomparsa di intere popolazioni, per esempio di una popolazione di pesci in un lago.

i) Sociologia.

Gli studi dei sociologi indicano decisamente che la formazione della ‛pubblica opinione' (che può essere definita in vari modi) è un fenomeno collettivo, il cui meccanismo fondamentale è stato chiarito grazie agli esperimenti condotti da S. Asch (v., 1952). In questi esperimenti si chiede a una decina di persone di indicare quale fra tre segmenti di diversa lunghezza sia lungo quanto un quarto segmento, di riferimento. A parte un autentico soggetto dell'esperimento, tutti gli altri sono collaboratori dello sperimentatore, cosa che il vero soggetto ignora. In una prima fase gli assistenti dello sperimentatore danno la risposta corretta (e il soggetto dell'esperimento pure). Nelle fasi successive tutti gli assistenti danno una risposta errata e circa il 60% dei soggetti dell'esperimento dà a sua volta una risposta errata. Ciò mostra chiaramente come gli individui siano influenzati dalle opinioni altrui. Questi risultati sono stati confermati dagli esperimenti sul campo condotti da E. Noelle-Neumann (v., 1980). Il fatto che gli individui, all'atto di formarsi un'opinione, esercitino un'influenza reciproca rende il problema della formazione della pubblica opinione accessibile ai metodi e ai concetti della sinergetica. In particolare, in presenza di determinate condizioni esterne (situazione dell'economia, aumento delle tasse, ecc.), la pubblica opinione può subire drammatici mutamenti, il cui esito può essere persino una rivoluzione.

l) Caratteristiche comuni agli esempi sopra riportati.

In tutti i casi considerati i sistemi consistevano di moltissimi sottosistemi. Al mutare, anche in maniera non particolare, di determinate condizioni esterne (per es. la potenza in entrata in un laser, l'inquinamento, ecc.) i sistemi possono sviluppare nuovi tipi di configurazioni su scala macroscopica. Un sistema può passare da uno stato omogeneo, indifferenziato, quiescente a uno stato non omogeneo ma ben ordinato, oppure a uno fra molteplici stati ordinati possibili. Questi sistemi possono esser fatti funzionare in stati stabili differenti (bistabilità o multistabilità): perciò possono essere usati, per esempio, nei calcolatori come elementi di memoria (ogni stato stabile rappresenta un numero, per es. 0 o 1). Nello stato ordinato possono aver luogo oscillazioni di vario tipo con un'unica frequenza o basate su una molteplicità di frequenze (oscillazioni quasi periodiche). Il sistema può anche presentare moti casuali (caos). Inoltre possono formarsi diverse configurazioni spaziali, per esempio strutture a ‛nido d'ape', onde o spirali.

In senso più astratto, nei ‛sistemi' sociali, culturali o scientifici possono nascere e svilupparsi nuove configurazioni: idee, concetti, paradigmi. La sinergetica cerca di elaborare concetti generali e metodi matematici per affrontare questi problemi da un punto di vista unificato.

4. I concetti fondamentali e gli strumenti matematici della sinergetica.

a) Concetti fondamentali e terminologia.

I concetti fondamentali della sinergetica sono quelli di ‛sistema', ‛parametro di controllo', ‛instabilità', ‛parametro d'ordine' e ‛asservimento'. Questi concetti sono definiti come segue.

1. Sistemi. Molti elementi singoli possono interagire l'uno con l'altro e così formare un sistema. Per esempio, una molecola è un sistema composto di atomi, una cellula è un sistema composto di parecchi sottosistemi, come biomolecole, membrane, ecc., una società è un sistema composto di individui.

2. Parametri di controllo. Un sistema è soggetto a influenze esterne, come l'apporto (input) di energia, l'apporto di materia, la temperatura, ecc. Queste grandezze possono essere caratterizzate mediante certi numeri detti parametri di controllo.

3. Instabilità. Quando i parametri di controllo variano, i sistemi possono reagire in due modi diversi. In ‛condizioni normali' una piccola variazione di un parametro di controllo determina soltanto una piccola variazione del sistema, senza produrre uno stato macroscopico qualitativamente nuovo. Esistono, però, valori critici del parametro di controllo, in corrispondenza dei quali anche un minimo mutamento del valore del parametro provoca un drastico cambiamento dello stato macroscopico del sistema, per esempio l'insorgere di oscillazioni, di configurazioni spaziali, l'innesco di un processo di differenziamento cellulare, ecc.

4. Parametri d'ordine. Quando si è raggiunto un nuovo stato ordinato, o, in altre parole, un nuovo assetto qualitativo del sistema, non basta descrivere il sistema in termini dei suoi elementi microscopici, ma è necessario far ricorso a concetti nuovi. Il concetto di parametro d'ordine serve appunto a questo scopo: i parametri d'ordine, infatti, sono grandezze che descrivono lo stato macroscopico del sistema. Per esempio, nel caso di un'onda, la sua ampiezza ha il carattere di un parametro d'ordine. Descriveremo in seguito come i parametri d'ordine possano essere determinati in modo matematicamente rigoroso.

5. Asservimento. In corrispondenza di un punto di instabilità si possono definire diversi ‛modi' collettivi, ovvero diversi tipi di comportamento collettivo. Mentre alcuni di questi modi sono persistenti e coincidono con i parametri d'ordine, molti altri modi collettivi tendono a smorzarsi. (In seguito daremo una definizione precisa di modo ‛persistente' e ‛smorzato'). Il comportamento di questi modi smorzati è completamente governato dai parametri d'ordine, tanto che si può dire che questi modi sono ‛asserviti' ai parametri d'ordine. Secondo il principio di asservimento, nei punti di instabilità il comportamento del sistema nella sua totalità è governato da pochissimi gradi di libertà (i parametri d'ordine), mentre tutti gli altri gradi di libertà sono soppressi. Questi pochi gradi di libertà determinano il comportamento macroscopico del sistema totale.

Dal punto di vista metodologico, la sinergetica è collegata con molte discipline, come la termodinamica, la termodinamica irreversibile, la teoria generale dei sistemi, la teoria dinamica dei sistemi, la teoria delle biforcazioni, la teoria dei processi stocastici, la teoria dei gruppi, la teoria dell'informazione, ecc.

b) Impostazione matematica.

Un sistema come quelli considerati precedentemente può essere descritto mediante opportune variabili, che indicheremo coi simboli q₁, q₂, ..., q_n. Queste variabili possono anche dipendere, come succede nei fluidi, dalla coordinata spaziale x. Esempi di queste variabili sono: i campi di densità e di velocità nei fluidi o nei plasmi, la concentrazione di molecole in reazioni chimiche, l'intensità del campo elettrico, la polarizzazione atomica e l'inversione nei laser, il numero di specie di un certo tipo, il numero di persone con una determinata opinione politica, ecc.

Tutte le variabili q_j dipendono, in generale, dal tempo t. D'ora in poi riuniremo tutte queste variabili, che descrivono un sistema, in un vettore di stato:

(q₁(t), q₂(t), ..., q_n(t)) = q(t). (51)

Si postula che l'evoluzione temporale del sistema possa essere descritta da equazioni differenziali della forma

in cui N è una funzione non lineare dei suoi argomenti. Nei mezzi continui N può contenere derivate rispetto allo spazio e α è un parametro di controllo singolo o un insieme di siffatti parametri. Le forze fluttuanti F, che possono dipendere dal tempo t, dallo spazio x e, in alcuni casi, dalla variabile di stato q, tengono conto del rumore interno e di quello esterno. Se F è indipendente da q, le equazioni (52) hanno la forma di un'equazione di Langevin. Negli altri casi, le (52) devono essere sostituite da equazioni differenziali stocastiche, secondo il calcolo di Îto oppure di Stratonovich. Per descrivere l'evoluzione temporale del sistema, anziché le (52), si possono anche usare equazioni stocastiche, per lo più postulando che abbia luogo un processo di Markov. L'ipotesi che il processo sia markoviano implica che la probabilità P(q, t) di trovare il sistema in un certo stato q al tempo t dipende solo dalla distribuzione di probabilità nell'istante immediatamente precedente e non in quelli ancora precedenti. Sotto questa ipotesi si può derivare un'equazione di Chapman-Kolmogorov o una master equation della forma

Ñ(q, t) = LP(q, t), (53)

dove L è un operatore lineare che determina transizioni fra differenti stati q del sistema. Nel caso di un processo di Markov continuo, L diventa un operatore differenziale lineare che contiene derivate rispetto a q_j fino al second'ordine e la (53) assume la forma di un'equazione di Fokker-Planck:

I K sono detti ‛coefficienti di deriva', i Q coefficienti di diffusione.

In seguito mostreremo come si studi l'equazione (52). I risultati che si ottengono per mezzo dell'equazione (53) sono molto simili.

Il punto cruciale dell'intera impostazione consiste nello studio del comportamento del sistema nei punti di instabilità. In corrispondenza di questi punti le fluttuazioni sono essenziali e quindi devono essere incluse nell'analisi. Se le forze fluttuanti non sono troppo intense, si può procedere attraverso i tre passaggi seguenti.

1. Un'analisi lineare di stabilità senza fluttuazioni ci permette di definire modi stabili (smorzati) e instabili (non smorzati).

2. Si trasformano le equazioni (52), forze fluttuanti incluse, adottando nuove variabili basate sui modi definiti in 1.

3. Si esprimono tutte le ampiezze dei modi smorzati tramite quelle dei modi non smorzati o instabili (principio di asservimento), comprese le fluttuazioni.

Per semplicità, in un primo tempo non prenderemo esplicitamente in considerazione le variazioni spaziali; solo in un secondo momento includeremo questi effetti nella nostra analisi.

Analisi lineare di stabilità. - Supponiamo che per un certo valore α₀ del parametro di controllo α l'equazione

q•= N(q, α) (55)

possegga una soluzione stabile:

α₀ : q⁰(t, x, α₀). (56)

Supponiamo ora che questa soluzione possa essere estesa al caso che α assuma un valore diverso da α₀. Per esempio, al variare del parametro di controllo, un liquido può permanere in stato di quiete, o un laser può non agire ancora come produttore di luce coerente. Ma può accadere che in corrispondenza del nuovo valore di α la soluzione

q⁰(t, x, a) (57)

diventi instabile. Per poter studiare la stabilità o l'instabilità, facciamo la seguente ipotesi:

q = q⁰ + u, (58)

dove u rappresenta una piccola deviazione da q⁰. Inserendo la (58) nella (55), facendo uso della relazione

q• = N(q⁰, α) (59)

e tenendo conto del fatto che u è piccolo, si trova un'equazione lineare in u della forma seguente:

u = L(q⁰(t, x))u. (60)

Nella (60) L è un operatore lineare: per sistemi discreti, è una matrice e, per sistemi continui, è un operatore che agisce sulle variabili spaziali. Discuteremo per primo il caso in cui L non contenga derivate spaziali e q⁰ sia indipendente dallo spazio. Se il sistema è inizialmente in quiete, q⁰ ed L non dipendono dal tempo. Le soluzioni della (60) hanno la forma generale

u(t) = e^λt v, (61)

dove v è un vettore indipendente dal tempo, se i λ non sono degeneri. Se la parte reale di λ è non negativa, la (61) è detta instabile, se è negativa, stabile. Se q⁰ descrive un'oscillazione, cioè se è periodica, lo è anche L. In questo caso, in base al teorema di Floquet, la soluzione della (60) è

u(t) = e^λt v(t), (62)

dove v(t) è una funzione periodica, purché i λ non siano degeneri (altrimenti in v può comparire un numero finito di potenze di t).

Può darsi che q⁰ e quindi L siano quasi periodiche. In tal caso q⁽⁰⁾(t) ha la forma generale

dove si può supporre che i rapporti fra le frequenze ω_j siano irrazionali. Per quanto il problema di determinare la forma della soluzione u in questo caso non sia risolubile in generale, si riesce a trattare un certo numero di casi speciali importanti. Uno di questi, di particolare rilievo per il nostro problema, è il seguente.

Definiamo come segue gli esponenti caratteristici generalizzati:

Facciamo ora le seguenti ipotesi: che tutti gli esponenti caratteristici generalizzati λ_j differiscano l'uno dall'altro, che l'angolo formato da due diverse soluzioni u resti finito anche per t → ∞, e che sia soddisfatta la cosiddetta condizione di Kolmogorov-Arnold-Moser (KAM)

∣ ω₁k₁ + ω₂k₂ + ... + ω_Nk_N ∣ > K ∣ k ∣^-δ, (65)

dove i k_j sono numeri interi. Allora la soluzione della (60), con L quasi periodica, ha la forma

u(t) = e^λt v(t), (66)

dove v(t) è una funzione quasi periodica che ha la stessa struttura della (63). A questa soluzione si può dare una forma più dettagliata, se si considera il problema (60) come un caso particolare di quello in cui si sia ovunque sostituito ω_jt con ω_jt + ϕ_j. È allora possibile mostrare che v nella (66) diventa una funzione periodica dei parametri ϕ₁, ..., ϕ_n.

c) Costruzione di soluzioni di biforcazione per risolvere le equazioni non lineari (52).

I risultati del paragrafo b possono essere estesi al caso in cui L sia un operatore che agisce sulle variabili spaziali. In tal caso, in generale, L è un operatore ellittico che, unitamente alle condizioni al contorno, ammette un insieme di autosoluzioni spaziali. Le soluzioni dipendono dalla forma del contorno, rettangolare o circolare in due dimensioni, cubica o sferica in tre dimensioni, ecc. La dipendenza generale dal tempo, quale compare nella (61), nella (62) o nella (66), resta la stessa, ma le funzioni v sono ora anche funzioni delle coordinate spaziali.

Costruiamo la soluzione generale delle equazioni (52) completamente non lineari. Poniamo

Gli indici u ed s contraddistinguono i modi stabili e quelli instabili, quali sono stati definiti mediante l'analisi lineare di stabilità. Le ampiezze ξ e le fasi ϕ sono funzioni del tempo ancora ignote.

Introducendo la (67) nella (51) e proiettando sulle funzioni v, Si trovano equazioni per le ξ e le ϕ che hanno la seguente forma:

Le F sono proiezioni delle forze fluttuanti dell'equazione (52) sui coefficienti di sviluppo v. Purché tutte le quantità λ_s, abbiano parti reali negative e le ξ_u e gli N siano abbastanza piccoli, si possono esprimere le funzioni ξ_s univocamente ed esplicitamente mediante ξ_u, ϕ e F_u, cioè

ξ_s = ξ_s(ξ_u, ϕ, F_u). (71)

Questa è la forma matematica del principio di asservimento. Questa eliminazione si può conseguire o tramite una costruzione esplicita o attraverso teoremi di esistenza. Se si trascurano le fluttuazioni, il teorema della varietà centrale, il teorema della varietà lenta e le tecniche di eliminazione adiabatica sono contenuti come casi particolari in quest'impostazione. Inserendo la (71) nella (68) e nella (69) si ottiene un sistema chiuso di equazioni per ξ_u e ϕ soltanto. ξ_u e ϕ si chiamano parametri d'ordine e le loro equazioni ‛equazioni dei parametri d'ordine'. Nel caso di mezzi continui illimitati, gli autovalori costituiscono un continuo. Per aggirare le difficoltà matematiche che insorgono in corrispondenza del punto di instabilità, al posto della (67) si possono formare ‛pacchetti d'onda' sommando su valori discreti di un vettore d'onda k; si tiene conto dello spettro continuo lasciando che ξ_u e ξ_s diventino funzioni lentamente variabili dello spazio. In questo caso λ_u diventa un operatore differenziale che agisce sulla coordinata spaziale.

d) Esempi.

Illustriamo con alcuni esempi il contenuto delle equazioni dei parametri d'ordine e le loro soluzioni.

Equazioni di Ginzburg-Landau generalizzate. - Cominciamo da una q₀ indipendente dallo spazio e dal tempo e studiamo l'evoluzione di configurazioni spaziali. In un dominio illimitato le equazioni dei parametri d'ordine assumono la forma seguente:

dove i puntini indicano coefficienti costanti, F_u sono forze fluttuanti e Δ è l'operatore di Laplace. Queste equazioni si possono considerare come generalizzazioni delle equazioni di Ginzburg-Landau, valide per sistemi in equilibrio termico che presentano una transizione di fase, come superconduttori e ferromagneti. In particolare, nel caso di un unico parametro d'ordine e in assenza di termini quadratici in ξ_u, le equazioni (72) assumono la forma familiare dell'equazione di Ginzburg-Landau:

ξ = (λ + Δ)ξ − ξ³ + F. (73)

Dalle equazioni (72), del tipo di quella di Langevin, si può derivare un'equazione di Fokker-Planck. In certi casi di importanza pratica, i parametri d'ordine soddisfano il cosiddetto ‛principio del bilancio dettagliato', che permette di ottenere la soluzione stazionaria dell'equazione di Fokker-Planck. Nel caso della (73) questa soluzione è

dove N è un fattore di normalizzazione e ξ = ξ(x). f è identico al famoso funzionale di Ginzburg-Landau per sistemi in equilibrio termico prossimi ai punti di transizione di fase; tuttavia, in questo caso, si riferisce a sistemi lontani dall'equilibrio termico ed è stato derivato da principî primi.

Le equazioni (72) si applicano a sistemi molto diversi fra loro - fluidi, laser, reazioni chimiche che si trovino in prossimità del loro primo punto di transizione - e mettono in evidenza l'universalità del comportamento di questi sistemi a prescindere dalla natura specifica dei loro sottosistemi.

Biforcazione di Hopf in mezzi spazialmente omogenei (per esempio in un reattore a vasca chiusa in continuo movimento). - In prima approssimazione, le equazioni dei parametri d'ordine assumono la forma seguente:

ξ = (λ′ + iλ′′)ξ − aξ ∣ ξ ∣²(+ ...) + F, (75)

dove λ = λ′ + iλ′′ e ξ sono grandezze complesse. Il fuoco stabile presente per α = α₀ è ora sostituito da un ciclo limite, cioè da un moto periodico. Le fluttuazioni di F provocano piccole fluttuazioni di ampiezza e una diffusione di fase.

Biforcazione di tori. - Se i parametri di controllo cambiano ulteriormente, un ciclo limite può biforcarsi in un moto più complicato contenente parecchie frequenze (moto quasi periodico). Questo moto può essere rappresentato da una traiettoria di parametri d'ordine giacente su un toro (v. fig. 36). Variando ancora i parametri di controllo, un toro può biforcarsi in altri tori, anche di dimensione superiore. In certe condizioni, un toro può decadere in cicli limite. Inoltre i cicli limite possono biforcarsi in cicli limite di periodo doppio. Infine, può presentarsi una nuova classe di fenomeni: il caos.

e) Il caos.

Il termine ‛caos' è invalso come termine tecnico per indicare l'evoluzione temporale irregolare di un sistema descritto da equazioni completamente deterministiche (v. fig. 37). Queste equazioni possono essere equazioni differenziali o trasformazioni relative a istanti di tempo discreti. Già tre equazioni differenziali ordinarie del primo ordine con uno o due accoppiamenti non lineari fra le variabili possono dar luogo al caos. Analogamente per un'equazione differenziale del second'ordine con una non linearità e una forza pilota periodica si può presentare lo stesso effetto. A seconda dei valori dei parametri di controllo, può verificarsi un comportamento regolare, per esempio un moto periodico, o un comportamento caotico.

Descriviamo ora alcuni dei più tipici risultati relativi a processi discreti descritti da trasformazioni su un intervallo. Introduciamo degli istanti di tempo discreti, k = 1, 2, ..., e la trasformazione

x_k+1 = rx_k(1 − x_k) (76)

sull'intervallo 0 − 1. L'equazione (76) si può risolvere con un calcolatore. A seconda dei valori di r, si possono trovare diversi tipi di comportamento di x_k in funzione di k. All'aumentare di r, si ha dapprima una soluzione costante della (76), che è stabile. Questa soluzione poi si biforca, in corrispondenza di r₁, in una soluzione periodica, che, in corrispondenza di r₂, si biforca in soluzioni con frequenza doppia, ecc. Pertanto, ogni volta, in corrispondenza dei valori r₁, r₂, r₃, ... del parametro, si verifica un raddoppiamento del periodo (v. fig. 38). I valori in corrispondenza dei quali avvengono questi raddoppiamenti del periodo obbediscono a una semplice legge:

si può mostrare che il numero che compare nella (77) è una costante universale per una certa classe di trasformazioni che presentino un massimo e che soddisfino certe altre condizioni. Per r = r_∞, sopravviene il caos, che è poi interrotto da ‛finestre' di comportamento regolare se r vien fatto crescere ulteriormente.

Si possono derivare leggi generali se si utilizzano trasformazioni di tipo rumore della forma

x_k+1 = f(x_k) + η_k, (78)

in cui η_k è una variabile casuale. L'equazione (78) si può considerare come l'analoga, per istanti di tempo discreti, dell'equazione di Langevin per x(t), ú = g(x) + F(t), dove t è il tempo e F(t) è una forza casuale. Similmente si può costruire anche l'analoga di un'equazione di Fokker-Planck, nella forma di un'equazione di Chapman-Kolmogorov per la distribuzione di probabilità P(x, k):

Nella (79) f(x) è la funzione di trasformazione che compare nella (78) e W rappresenta la distribuzione di probabilità del rumore η.

La (79) può essere generalizzata al caso di molte variabili. Si ha

x_k+1 = f(x_k) + G(x_k)g_k (80)

e

dove D è il determinante di G. Le equazioni (79) e (81) possono essere risolte per iterazione nella forma di integrali sui cammini. Nel caso di trasformazioni lineari, cioè

f(x_k) = A x_k, (82)

la soluzione esatta dell'equazione (81) con D = cost. e W gaussiana è

con

È anche possibile generalizzare il principio di asservimento al caso dell'equazione di Chapman-Kolmogorov (81). Tramite l'ipotesi

P(ξ_u, ξ_s, k) = h(ξ_s ∣ ξ_u, k) g(ξ_u, k), (87)

si può derivare un'equazione integrale per il solo g. In questo modo molti dei risultati precedenti, validi per equazioni continue, possono essere resi validi per equazioni discrete. Inoltre diventa possibile ottenere una visione generale del fenomeno per tutti i valori dei parametri di controllo, come r, il che permette di derivare regole di scala per differenti regioni dei parametri di controllo. In particolare, in un certo numero di casi, al crescere dei parametri di controllo, si trovano regimi periodici o multiperiodici che si alternano a regimi caotici.

5. Conclusione.

I risultati presentati in questo scritto mostrano che sistemi molto diversi, che interessano svariati campi - la fisica, la chimica, la biologia, l'economia, la sociologia -, possono essere trattati facendo ricorso agli stessi principî.

Quando mutano le condizioni esterne descritte dai parametri di controllo, improvvisamente possono formarsi in modo autoorganizzato nuove strutture, di solito altamente ordinate. I metodi della sinergetica permettono di trattare tutti questi differenti sistemi esattamente nello stesso modo, grazie ai concetti di parametro d'ordine e di asservimento.

Un confronto fra i concetti della termodinamica e della termodinamica irreversibile, da una parte, e quelli della sinergetica, dall'altra, ne mette in luce la fondamentale differenza. In termodinamica svolge un ruolo centrale l'entropia, una grandezza ‛statica', come risulta chiaramente dalla relazione di Boltzmann. La termodinamica irreversibile si basa ancora largamente sul concetto di entropia e tiene conto delle variazioni nel tempo dei sistemi solo in modo molto globale. La sinergetica si basa su un principio dinamico: è la specifica variazione temporale di modi collettivi che porta alle varie configurazioni dei sistemi non in equilibrio.

Bibliografia.

Arnold, L., Lefever, R. (a cura di), Stochastic nonlinear systems in physics, in Springer series in synergetics (a cura di H. Haken), vol. VIII, Berlin-Heidelberg-New York 1981.

Asch, S. E., Social psychology, New York 1952.

Becker, R., Theory of heat, Berlin-Heidelberg-New York 1967.

Blumenfeld, L.A. (a cura di), Problems of biological physics, in Springer series in synergetics (a cura di H. Haken), vol. VII, Berlin-Heidelberg-New York 1981.

Boltzmann, L., Vorlesungen über Gastheorie, 2 voll., Leipzig 1896-1898.

Callen, H. B., Thermodynamics, New York 1960.

De Groot, S. R., Mazur, P., Non-equilibrium thermodynamics, Amsterdam 1962.

Della Dora, J., Demongeot, J., Lacolle, B. (a cura di), Numerical methods in the study of critical phenomena, in Springer series in synergetics (a cura di H. Haken), vol. IX, Berlin-Heidelberg-New York 1981.

Glansdorff, P., Prigogine, I., Thermodynamics of structure, stability and fluctuations, New York 1971.

Güttinger, W., Eikemeier, H. (a cura di), Structural stability in physics, in Springer series in synergetics (a cura di H. Haken), vol. IV, Berlin-Heidelberg-New York 1979.

Haase, R., Thermodynamics of irreversible processes, Reading, Mass., 1969.

Haken, H., Cooperative phenomena in systems far from thermal equilibrium and in nonphysical systems, in ‟Review of modern physics", 1975, XLVII, 1, pp. 67-121.

Haken, H., Synergetics, an introduction, in Springer series in synergetics (a cura di H. Haken), vol. I, Berlin-Heidelberg-New York 1977, nuova ed. 1978.

Haken, H. (a cura di), Synergetics. A workshop, in Springer series in synergetics (a cura di H. Haken), vol. II, Berlin-Heidelberg-New York 1977.

Haken, H. (a cura di), Pattern formation by dynamic systems and pattern recognition, in Springer series in synergetics (a cura di H. Haken), vol. V, Berlin-Heidelberg-New York 1979.

Haken, H. (a cura di), Dynamics of synergetic systems, in Springer series in synergetics (a cura di H. Haken), vol. VI, Berlin-Heidelberg-New York 1980.

Haken, H. (a cura di), Chaos and order in nature, in Springer series in synergetics (a cura di H. Haken), vol. XI, Berlin-Heidelberg-New York 1981.

Haken, H., Graham, R., Synergetik, die Lehre vom Zusammenwirken, in ‟Umschau in Wissenschaft und Technik", 1971, VI, pp. 191-195.

Klimontovich, Y. L. (a cura di), The kinetic theory of electromagnetic processes, in Springer series in synergetics (a cura di H. Haken), vol. X, Berlin-Heidelberg-New York 1982.

Kubo, R., Thermodynamics, Amsterdam 1968.

Landau, L. D., Lifschitz, E. M., Statistical physics, in Course of theoretical physics, vol. V, London-Paris 1952.

Landauer, R., Stability and entropy production in electrical circuits, in ‟Journal of statistical physics", 1975, XIII, pp. 1-16.

Landauer, R., Inadequacy of entropy and entropy derivatives in characterizing the steady state, in ‟Physical review", 1975, AXII, pp. 636-638.

Landsberg, P. T., Thermodynamics, New York 1961.

Meixner, J., Reik, H. G., Thermodynamik der irreversiblen Prozesse, in Handbuch der Physik. Encyclopaedia of physics (a cura di S. Flügge), vol. III, 2, Berlin-Heidelberg-New York 1959.

Münster, A., Statistical thermodynamics, vol. I, Berlin-Heidelberg-New York 1969.

Nicolis, G., Irreversible thermodynamics, in ‟Reports on progress in physics", 1979, XLII, pp. 225-268.

Noelle-Neumann, E., Die Schweigespirale, München 1980.

Onsager, L., Reciprocal relations in irreversible processes I., in ‟Physical review", 1931, XXXVII, pp. 405-426.

Pacault, A., Vidal, C. (a cura di), Synergetics far from equilibrium, in Springer series in synergetics (a cura di H. Haken), vol. III, Berlin-Heidelberg-New York 1979.

Prigogine, I., Étude thermodynamique des processes irréversibles, Liège 1947.

Prigogine, I., Introduction to thermodynamics of irreversible processes, New York 1955.

Prigogine, I., Non-equilibrium statistical mechanics, New York 1962.

Thomson, W., On a universal tendency in nature to the dissipation of mechanical energy, in ‟Proceedings of the Royal Society of Edinburgh", 1854, III, p. 139.

Zubarev, D. N., Non-equilibriums statistical thermodynamics, New York-London 1974.