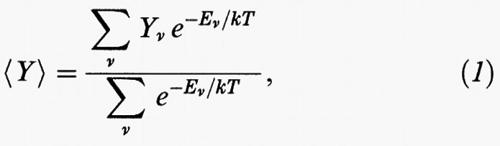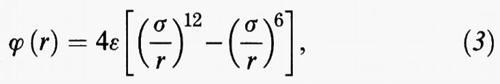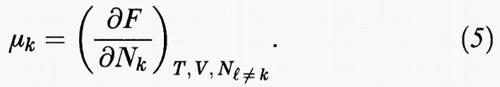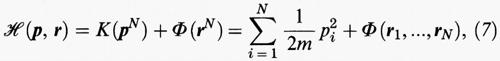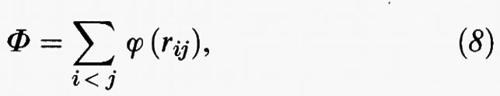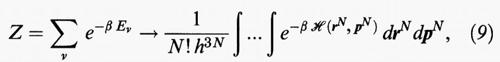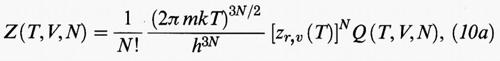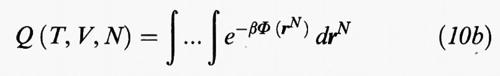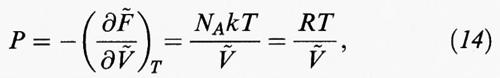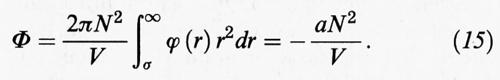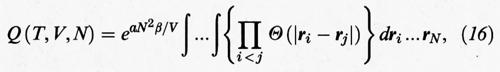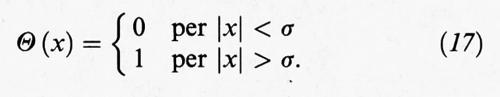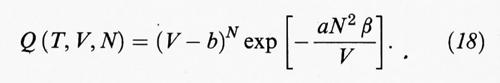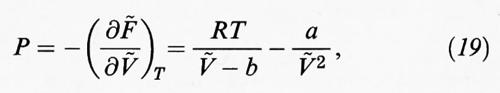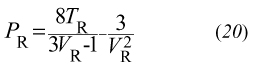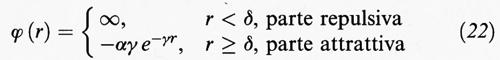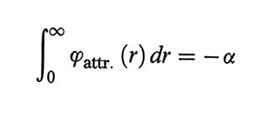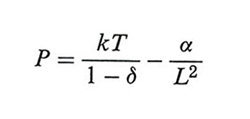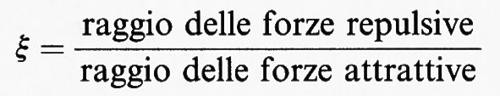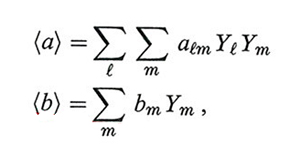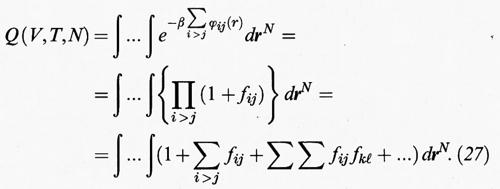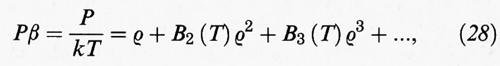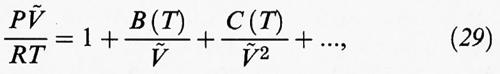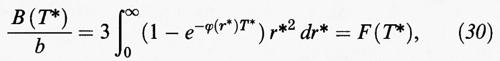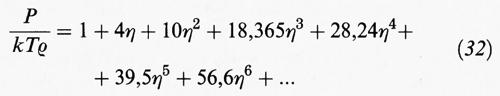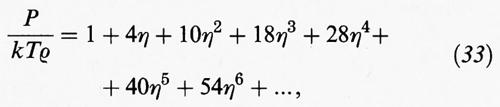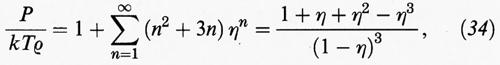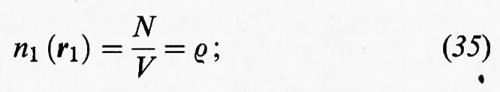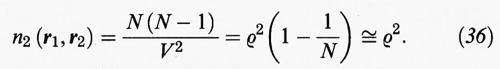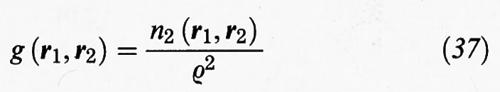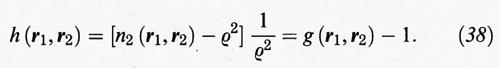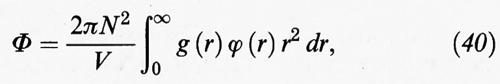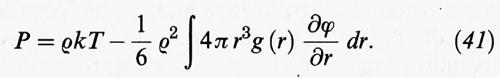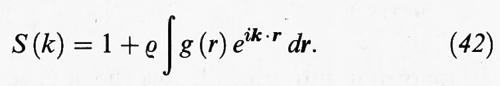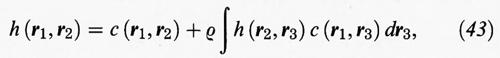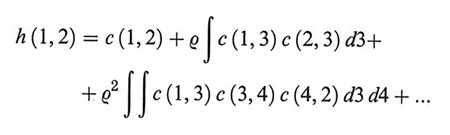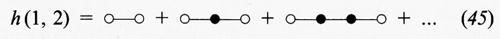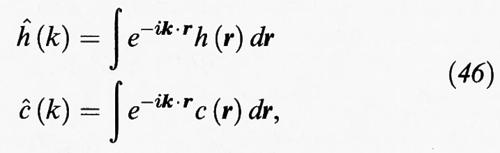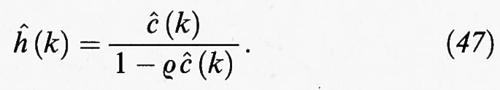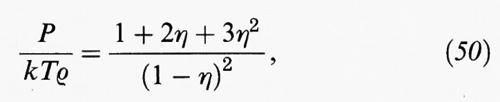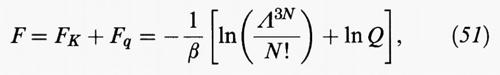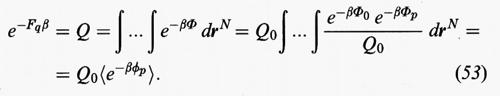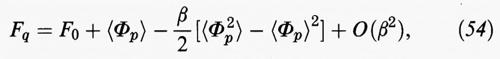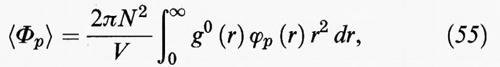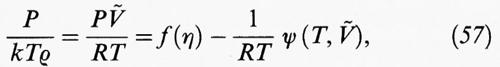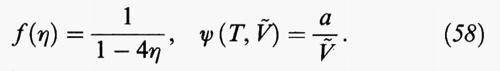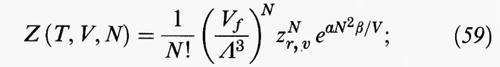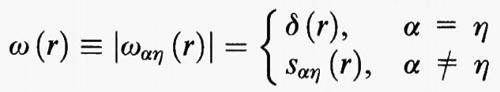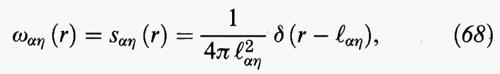Termodinamica molecolare

Termodinamica molecolare

SOMMARIO: 1. Modelli molecolari e proprietà termodinamiche.  2. Presupposti per valutare le proprietà termodinamiche. 3. Teoria di van der Waals. 4. Sviluppo viriale. 5. Impiego delle funzioni di distribuzione.  6. Metodi perturbativi.  7. Estensione della teoria di van der Waals alle molecole complesse.  8. Impiego delle funzioni di distribuzione per fluidi con molecole complesse.  9. Conclusioni. □ Bibliografia.

1. Modelli molecolari e proprietà termodinamiche

La termodinamica molecolare si propone di studiare gli stati di equilibrio della materia utilizzando in larga misura le informazioni attualmente disponibili sulla configurazione geometrica delle molecole e sulla natura delle forze della loro interazione reciproca, dette forze intermolecolari. Pertanto essa costituisce una sintesi della termodinamica classica, di quella statistica e della chimica-fisica molecolare, ma ha ormai acquistato un respiro e una caratterizzazione tali da poter rivendicare una ben definita autonomia.

La termodinamica molecolare trova ovviamente piena motivazione scientifica non solo in quanto si propone di comprendere alcuni aspetti delle proprietà della materia, ma anche in quanto essa risponde ad alcuni problemi posti dallo sviluppo di talune moderne tecnologie. Di notevole importanza risulta, ad esempio, il ruolo che essa occupa nella predizione della distribuzione dei componenti presenti nelle diverse parti omogenee, o fasi (gas, liquidi, solidi), di un sistema eterogeneo in condizioni di equilibrio. La ricaduta delle conoscenze così ottenute è stata utilizzata nella progettazione e nello sviluppo dei processi di separazione, nella caratterizzazione dei materiali costituiti da miscele di sostanze in cui sono presenti dispersioni con più fasi, nello studio della distribuzione dei componenti dell'atmosfera fra le diverse fasi in essa presenti (gas, liquidi in gocce, particelle solide), nello studio della distribuzione degli idrocarburi nei giacimenti petroliferi e così via.

I diversi stati di aggregazione della materia sono schematicamente rappresentati, a livello sia macroscopico che microscopico, nella fig. 1. In un diagramma pressione-densità vengono riportate le linee che separano le regioni di coesistenza di due fasi in equilibrio; la linea tratteggiata indica invece una particolare isoterma - detta isoterma critica - che passa per un punto, al confine fra le fasi liquida e gassosa, in corrispondenza del quale presenta un flesso orizzontale. Nei diversi riquadri vengono mostrate alcune simulazioni, condotte su molecole sferiche, che evidenziano sia la loro distribuzione in un determinato istante, sia la loro traiettoria per un particolare intervallo di tempo.

Tali simulazioni costituiscono un significativo risultato dell'applicazione dei calcolatori alla descrizione del comportamento della materia. Si considerano dei sistemi modello costituiti da alcune centinaia di molecole, contenuti in un determinato volume e si effettua la media fra diverse loro distribuzioni, o configurazioni, costruite a caso (v. fig. 2) compatibilmente con le caratteristiche degli oggetti stessi (ad esempio, molecole rappresentate da sfere dure non possono compenetrarsi). Il valore medio all'equilibrio, detto ‛canonico', di una grandezza osservabile Y viene valutato come segue:

in cui k è la costante di Boltzmann, T la temperatura assoluta ed E_ν l'energia di una generica configurazione ν. Per un fluido di sfere dure tutte le possibili configurazioni hanno la stessa energia, per cui il termine esponenziale è uguale a zero, se esiste una sovrapposizione fra le sfere, o a 1 in caso contrario. Ne consegue che la media assume la seguente semplice forma:

essendo M il numero di configurazioni prese in esame.

A questo approccio a carattere puramente stocastico, che utilizza il metodo Monte Carlo, si affianca come alternativa la dinamica molecolare che, viceversa, simula in modo deterministico il movimento delle molecole mediante le equazioni della meccanica, che integrate a partire da assegnate condizioni iniziali danno le traiettorie molecolari.

I metodi di simulazione hanno ormai raggiunto un elevato grado di sofisticazione, soprattutto per quanto concerne la forma e le interazioni degli oggetti che rappresentano le molecole, e ci offrono un quadro dettagliato del comportamento microfisico della materia. Essi non ci affrancano però dalla necessità di formulare un quadro concettuale che ci permetta di prevedere quali siano gli stati stabili della materia in particolari condizioni di temperatura, pressione e composizione, e di valutarne i valori delle diverse grandezze termodinamiche.

Nella presente trattazione limiteremo la nostra analisi ai fluidi, ovvero ai liquidi, ai gas e alle loro miscele. Per poter procedere è anzitutto necessario definire alcuni opportuni modelli molecolari, prendendo in considerazione la struttura geometrica delle molecole e la forma delle loro interazioni reciproche.

Un fluido viene definito ‛semplice' se è costituito da un insieme di molecole tali che la funzione che esprime la loro energia di interazione - chiamata potenziale intermolecolare - sia di tipo ‛centrale', ovvero dipenda unicamente dalla distanza r fra i centri di massa delle molecole stesse. In senso stretto, rientrano in questa definizione solo i fluidi costituiti da gas monoatomici; in realtà appartengono ai fluidi semplici anche l'azoto, il metano, l'ossigeno, ecc., le cui molecole sono piccole, in senso relativo, e compatte.

Il più semplice modello molecolare è quello delle sfere dure, che hanno un diametro uguale a σ e un potenziale nullo per r ≫ σ, e tendente all'infinito per r ≤ σ (dove r è la distanza tra le sfere). Pur essendo poco realistico, come vedremo, questo modello si rivelerà molto utile per mettere in evidenza alcune importanti caratteristiche dei fluidi.

Una descrizione più corretta del potenziale intermolecolare è fornita dalla fig. 3A. Per r → ∞ il potenziale tende a zero, poiché si annulla l'energia di interazione fra le molecole stesse. A distanze elevate prevale l'interazione attrattiva - dovuta, secondo un modello formulato da F. W. London, all'interazione fra i dipoli oscillanti associati ai moti degli elettroni rispetto ai nuclei. Viceversa, a piccole distanze prevale la repulsione dovuta alla sovrapposizione delle nuvole elettroniche. La funzione che descrive il potenziale è caratterizzata da due parametri, σ ed ε, che rappresentano, rispettivamente, la distanza in corrispondenza della quale essa si annulla e il valore minimo che essa assume. Entrambi gli aspetti precedenti sono compendiati nella seguente espressione:

nota come potenziale di Lennard-Jones. L'interazione attrattiva risulta inversamente proporzionale alla sesta potenza della distanza, in accordo col menzionato modello di London, mentre l'interazione repulsiva viene posta come inversamente proporzionale alla dodicesima potenza della distanza.

Il potenziale centrale non risulta adeguato per le molecole nelle quali siano presenti dei legami eteroatomici, che generano nelle molecole dei momenti dipolari permanenti. In questo caso l'interazione elettrostatica fra i due dipoli dipende dall'orientazione relativa delle molecole stesse.

Per molecole aventi una struttura complessa, come ad esempio quelle di un idrocarburo di elevato peso molecolare o al limite di un polimero, l'interazione può essere decomposta nella somma dei diversi contributi relativi forniti dai gruppi atomici o dai singoli atomi presenti nella molecola. In conclusione, per agevolare la trattazione è opportuno classificare i fluidi sulla base delle caratteristiche delle molecole di cui sono costituiti, secondo lo schema riportato nella tab. I.

2. Presupposti per valutare le proprietà termodinamiche

In condizioni di equilibrio la valutazione delle proprietà termodinamiche viene effettuata attraverso la funzione di ripartizione canonica (v. meccanica statistica, vol. IV), definita come segue:

La somma è estesa a tutti gli stati quantici del sistema, aventi ciascuno energia E_ν; inoltre β = 1/kT, dove k è la costante di Boltzmann e T la temperatura assoluta.

La funzione energia libera di Helmholtz, F, è legata alla funzione di ripartizione Z attraverso la semplice relazione logaritmica riportata nello schema della tab. II, nella quale viene anche illustrato come la funzione energia libera permetta di calcolare le più comuni grandezze termodinamiche.

In una miscela di più componenti - che indicheremo con gli indici k, l, m  - la funzione Z (T, V, N) dipende anche dal numero N_k di molecole di ciascuno dei componenti stessi. Il potenziale chimico del k-esimo componente si ricava allora come segue:

La sua conoscenza è il prerequisito che permette di individuare le condizioni di equilibrio di un sistema nel quale siano presenti più fasi, che indicheremo con le lettere greche α, β, ... Infatti all'equilibrio vale la condizione di Gibbs, in base alla quale il potenziale chimico di ciascun componente deve avere lo stesso valore nelle diverse fasi presenti nel sistema:

La relazione precedente mette in evidenza il ruolo del potenziale chimico nell'individuare le condizioni di equilibrio relativamente al trasporto di materia, un ruolo equivalente a quelli svolti dalla temperatura nel caso dell'equilibrio termico e dalla pressione in quello dell'equilibrio meccanico.

In forma hamiltoniana l'energia totale di un fluido costituito da un numero N di molecole (N è uguale al numero di Avogadro N_A per una mole) si esprime come segue:

dove r_i e p_i sono i vettori che indicano rispettivamente la posizione e la quantità di moto dell'i-esima molecola, avente massa m. K è l'energia cinetica e Φ quella potenziale; quest'ultima in prima approssimazione può essere ottenuta sommando le energie potenziali di interazione delle diverse coppie di molecole nel modo seguente:

dove r_ij indica la distanza fra i loro centri.

Ciò premesso, è possibile dimostrare che la sommatoria attraverso la quale si valuta la funzione di ripartizione si può approssimare mediante un integrale sullo spazio delle fasi definito dalle coordinate e dalla quantità di moto delle singole molecole, come segue:

essendo dr^N = dr₁dr₂ ... dr_N, dp^N = dp₁dp₂ ... dp_N, mentre dr = dx dy dz indica l'elemento di volume. I fattori N! e h^3N tengono conto rispettivamente dell'indistinguibilità delle molecole e del fatto che lo spazio delle fasi rispetto al quale si effettua l'integrazione, in base alla meccanica quantistica, risulta diviso in cellette di volume h³.

Se nella (9) si sostituisce l'espressione (7) di ℋ, e si integra rispetto alle quantità di moto, si ottiene:

dove

viene chiamato integrale delle configurazioni.

Infine z_r,_v (T) rappresenta il contributo dovuto ai moti vibrazionali e rotazionali delle molecole, schematizzati nella fig. 4. La sua forma dipende dalle caratteristiche specifiche della molecola in esame. Tuttavia, in generale, non dipende dal volume del sistema e pertanto non contribuisce a determinarne il comportamento di stato, per cui non verrà per ora considerato esplicitamente.

In un gas perfetto non esistono interazioni fra le molecole, per cui Φ = 0, e quindi Q = V^N. In base alle relazioni della tab. II si ricava:

F = NkT [3Λ - 1 + ln N - ln V + ln z_r,_v (T)], (11)

dove Λ = h/(2π mkT)^1/2, e inoltre è stata legittimamente utilizzata l'approssimazione: ln N! ≅ N ln N - N. (12)

In generale se, come indicato nella tab. II, si deriva rispetto al volume l'espressione dell'energia libera e si eguaglia il risultato così ottenuto alla pressione cambiata di segno, si ottiene una relazione del tipo: P = f (T, V, N), (13), che costituisce l'equazione di stato del sistema in esame. Così, nel caso particolare di un gas perfetto, riferendoci a una mole, si ottiene:

dove la tilde indica il valore molare di una grandezza estensiva; R = N_Ak = 8,3145 J/mol K (che è la costante universale dei gas).

3. Teoria di van der Waals

La determinazione dell'equazione di stato dei fluidi reali richiede la conoscenza di una forma esplicita dell'integrale delle configurazioni Q (T, V, N). Il suo calcolo per sistemi di particelle interagenti costituisce in generale un problema di grande difficoltà, che può essere affrontato solo utilizzando opportune approssimazioni o particolari accorgimenti. Un approccio semplificato è quello di valutare l'energia potenziale cui è soggetta una molecola dalla media delle interazioni con quelle circostanti, ponendo che queste abbiano una distribuzione uniforme compatibile con la densità del fluido stesso. In altri termini, si assume che ciascuna molecola risulti soggetta a un campo medio di energia potenziale e che tale campo non venga alterato dall'influenza delle interazioni fluttuanti che si manifestano a corto raggio.

Assumiamo che il potenziale intermolecolare abbia la forma illustrata nella fig. 3B, in cui si assimilano le molecole a sfere dure di diametro σ, fra le quali si manifesta una forza attrattiva. L'energia potenziale Φ del fluido si può allora valutare seguendo lo schema illustrato nella fig. 5. Si considera infatti l'interazione di una molecola centrale con quelle contenute in una crosta sferica di volume 4πr²dr, assumendo che la loro distribuzione sia uniforme. Si integra quindi su tutto il volume per valutare l'interazione con tutte le molecole presenti nel sistema. In realtà, poiché la distanza entro la quale si manifesta tale interazione è piccola rispetto alle dimensioni del sistema, risulta legittimo estendere l'integrazione all'infinito per evitare di tener conto dell'andamento del potenziale alle pareti del recipiente. Per ottenere Φ è necessario moltiplicare il numero di molecole per N e dividere per 2 allo scopo di non contare due volte la stessa interazione. Si ottiene:

L'integrale è sicuramente convergente se ϕ (r) ∝ r^-n, con n > 3, e il suo valore è negativo.

Se si sostituisce la precedente espressione dell'energia potenziale in quella dell'integrale delle configurazioni, si ricava:

dove Θ (x) è la funzione a gradino definita come segue:

L'integrale che compare nell'espressione precedente può essere calcolato con esattezza solo per i sistemi monodimensionali di lunghezza L, e si ottiene (L - Nδ)^N/N!

Non si conosce la soluzione esatta per i sistemi a più di una dimensione; è però possibile proporne un'espressione approssimata mediante semplici considerazioni. Indichiamo anzitutto con b = (2/3) πσ³N = b₀ N il cosiddetto ‛covolume', che rappresenta, come illustrato nella fig. 6, il volume non accessibile alle molecole per la loro impenetrabilità dovuta alla parte ‛dura' del potenziale. Se V è grande rispetto a b, il valore dell'integrale si avvicina a V^N e si ricade nel caso del gas perfetto. Viceversa, se i due volumi sono dello stesso ordine, l'integrale tende rapidamente a zero. Tenendo conto di tutto ciò si può allora adottare la seguente formula, che costituisce una generalizzazione di quella ricavata per un fluido monodimensionale:

Se tale formula viene utilizzata per la valutazione della funzione di ripartizione Z (T, V, N), e quindi dell'energia libera, si ricava infine la seguente equazione di stato:

avendo posto N = N_A.

L'equazione di stato così ottenuta è stata proposta nel 1873 da J. D. van der Waals nella sua tesi di dottorato dal significativo titolo Sulla continuità fra gli stati liquido e gassoso. Infatti le isoterme che a essa corrispondono hanno gli andamenti illustrati nella fig. 7. A temperature elevate si avvicinano all'andamento dell'iperbole equilatera corrispondente a un gas perfetto, mentre esiste una temperatura ‛critica' in corrispondenza della quale l'isoterma presenta un flesso orizzontale. Per temperature inferiori le isoterme presentano un andamento sinuoso che permette di individuare, in base a una costruzione proposta da Maxwell e illustrata nella stessa fig. 7, la coesistenza tra le fasi liquida e gassosa.

La lezione presentata da van der Waals quando gli fu conferito il premio Nobel, nel 1910, conteneva le seguenti espressioni, che sembrano sancire la nascita della termodinamica molecolare: ‟È perfettamente chiaro che in tutti i miei studi ero assolutamente convinto della reale esistenza delle molecole, che non ho mai considerato come finzioni della mia immaginazione o semplici effetti dovuti a centri di forza. Al contrario, le ho considerate come corpi realmente esistenti". Per apprezzare il significato di questo brano si deve tenere presente che al tempo in cui van der Waals stava sviluppando la sua teoria i concetti di atomo e molecola non erano del tutto accettati dal mondo scientifico.

I parametri a e b dell'equazione di stato si possono mettere in relazione con i valori critici dei parametri di stato T_c, Ç_c, e P_c mediante le relazioni

impiegando le quali l'equazione di stato può essere riscritta in forma ridotta:

essendo P_R = P/P_c, T_R = T/T_c e V_R = Ç/Ç_c. L'equazione precedente non contiene parametri specifici di particolari fluidi e riflette una legge generale - la cui validità supera la stessa equazione di van der Waals che l'ha ispirata - nota come ‛legge degli stati corrispondenti'. Tutti i fluidi risultano descrivibili dalla stessa equazione di stato, purché espressa mediante le variabili ridotte P_R, V_R e T_R. In realtà, la precedente affermazione è rigorosamente valida solo per i fluidi semplici il cui potenziale di interazione è di tipo centrale.

È interessante osservare che è possibile migliorare in modo significativo la descrizione del comportamento di stato dei fluidi, mediante una piccola modifica dell'equazione (19), riscrivendola nella forma

nota come equazione di Redlich e Kwong (RK). Ovviamente i valori numerici dei parametri a e b differiscono da quelli corrispondenti alla (19) stessa.

Il processo di condensazione previsto dalla teoria di van der Waals è stato l'oggetto di un'analisi approfondita, iniziata nel 1961 da Kac, Uhlenbeck e Hemmer (v., 1963) e sviluppata successivamente da altri autori. Per esaminare questo aspetto è necessario osservare che alcune funzioni termodinamiche, come ad esempio l'energia libera, subiscono delle brusche variazioni in corrispondenza di una transizione di fase e pertanto perdono la loro analiticità. Se consideriamo la forma (4) della funzione di ripartizione, ciò non può verificarsi, a temperature diverse da zero, per sistemi costituiti da un numero finito, se pur molto elevato, di particelle. Si può ovviare all'inconveniente studiando il loro comportamento al cosiddetto limite termodinamico, corrispondente a V → ∞ e N → ∞, per ρ = V/N finito.

Consideriamo ora un fluido monodimensionale costituito da N molecole che si muovono su un segmento di lunghezza L e che interagiscono con un potenziale come quello illustrato nella fig. 3B. L'interazione viene espressa nella forma seguente:

tale per cui l'integrale

risulta indipendente dal parametro γ che ne caratterizza il raggio d'azione.

Per il sistema così definito, l'integrale delle configurazioni può essere calcolato esattamente anche al limite termodinamico; per valori finiti di γ non presenta transizioni di fase, in accordo con le ricerche che erano già state condotte sui sistemi monodimensionali. Tuttavia, se si valuta il limite del comportamento del fluido per γ → 0, rendendo così le forze intermolecolari molto deboli ma con raggio d'azione tendente all'infinito, si ricava la seguente equazione di stato di van der Waals:

che presenta una transizione di fase. La zona di coesistenza fra liquido e vapore risulta descritta da una isoterma orizzontale compatibile con la regola di Maxwell. Questo sorprendente risultato è stato successivamente esteso ai sistemi tridimensionali da E. R. van Kampen, J. L. Lebowitz e R. Penrose.

In conclusione, se si esprimono le funzioni termodinamiche mediante il rapporto

al limite termodinamico, per ξ ≪ 1, si prevede il fenomeno della condensazione e l'esistenza di un punto critico compatibilmente con la teoria di van der Waals. Questo risultato giustifica il successo della teoria, dovuto essenzialmente al criterio euristico di separare l'effetto delle forze attrattive da quello delle forze repulsive.

Infine ricordiamo che van der Waals ha proposto anche un approccio molto efficace per lo studio delle miscele a più componenti attraverso il concetto di fluido equivalente. La loro descrizione viene infatti condotta studiando il comportamento di stato di uno pseudo-fluido i cui parametri a e b dipendono dalla composizione mediante opportune regole di mescolamento, quali:

dove Y_l  e Y_m sono le frazioni molari dei componenti in gioco, espresse dal rapporto fra il numero delle loro molecole e il numero totale di molecole presenti nel sistema, e a_lm = √a_la_m.

Per miscele di più componenti l'equilibrio tra le fasi si determina, in accordo con la (6), imponendo l'eguaglianza fra i potenziali chimici, a loro volta valutati dall'espressione dell'energia libera mediante l'equazione (5). Seguendo questa impostazione si ottiene un sistema di equazioni algebriche non lineari le cui incognite sono le frazioni molari di ciascun componente nelle diverse fasi tra di loro in equilibrio.

4. Sviluppo viriale

Un metodo per calcolare l'integrale delle configurazioni è stato formulato da Joseph Mayer e Maria Göpper Mayer (v., 1940). Introducendo l'opportuna funzione, detta di Mayer,

f_ij = e^-βϕij(r) - 1, (26)

si può scrivere l'integrale delle configurazioni al modo seguente:

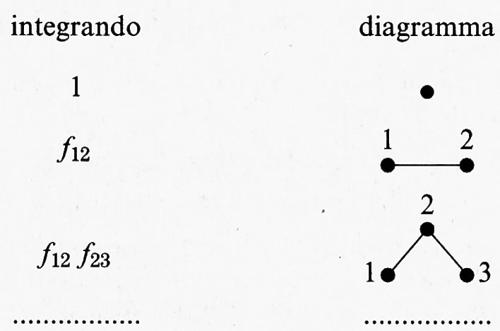
Il calcolo dei diversi termini presenti nella precedente espressione risulta agevolato dall'impiego di opportuni diagrammi. Se si indica con:

a ciascun termine dello sviluppo corrisponde un diagramma, come indicato nel seguente schema:

Risulta allora possibile individuare, come illustrato nella fig. 8, una successione di gruppi, o clusters, di molecole, contenenti tutti i possibili diagrammi che connettono, in modo diretto o indiretto, un determinato numero di punti. La trattazione dei coniugi Mayer offre le regole per valutare il contributo di ciascuno di tali gruppi all'integrale delle configurazioni. Si può osservare che tale impostazione presenta un'analogia con quella introdotta da R. P. Feynman nella soluzione dei complessi integrali funzionali della elettrodinamica quantistica e successivamente applicata nelle indagini sulle interazioni fra le particelle elementari. Questo fatto non deve stupire poiché il calcolo di Q (T, V, N) condotto su tutte le configurazioni costituisce un integrale funzionale.

La precedente trattazione porta a un'equazione di stato che ha la forma di uno sviluppo in serie di potenza della densità:

dove ρ = N/V è la densità molecolare. In forma diversa si può scrivere come segue:

una relazione nota come ‛equazione di stato del viriale', introdotta per la prima volta da H. Kamerlingh Onnes nel 1901. I diversi coefficienti viriali

B (T) = N_AB₂ (T), C (T) = N²_AB₃ (T), ...

riflettono rispettivamente le interazioni fra gruppi di due, tre, e così via, molecole. In particolare, se consideriamo un fluido con un potenziale intermolecolare di tipo centrale del tipo ϕ (r) = ε (r/σ), come ad esempio il potenziale di Lennard-Jones (3), si ricava la seguente espressione del secondo coefficiente viriale:

dove b è il covolume precedentemente definito, e

Nella fig. 9 viene riportato un confronto unificato tra il secondo coefficiente viriale, calcolato impiegando il potenziale di Lennard-Jones, e i valori sperimentali per una serie di molecole aventi una configurazione compatta, quali i gas rari, l'azoto, il metano. Purché si calibrino opportunamente i valori dei parametri ε e σ, si ottiene un eccellente accordo fra dati sperimentali e valori calcolati. Questo risultato costituisce una conferma della validità della legge degli stati corrispondenti per molecole soggette a un potenziale centrale. Calcoli analoghi sono stati condotti anche per il terzo coefficiente viriale. Purtroppo lo sviluppo del viriale, anche se viene arricchito di un numero sempre maggiore di termini, non converge in corrispondenza di elevate densità dei liquidi. Questo risultato mette in evidenza la necessità di affrontare il problema della continuità fra gli stati gassoso e liquido secondo un diverso approccio.

Prima di intraprendere una nuova strada è importante ricordare che, per sistemi di sfere dure, è stato possibile estendere i calcoli sino al settimo coefficiente viriale. Se invece della densità ρ si utilizza la cosiddetta frazione di impacchettamento,

data dal prodotto del volume di una molecola per la densità molecolare, l'equazione di stato del viriale assume la forma seguente:

Valori esatti (o pseudo-sperimentali) del comportamento di stato di un sistema di sfere dure sono stati ottenuti mediante metodi di simulazione con il calcolatore: ne sono risultati i punti riportati nella fig. 10. Per ottenere una soddisfacente descrizione di tali dati è necessario impiegare uno sviluppo viriale di almeno cinque termini.

Carnahan e Starling (v., 1972) hanno euristicamente proposto di correggere arbitrariamente l'equazione del viriale come segue:

rappresentabile con una serie infinita:

la quale converge verso un'espressione compatta che simula in modo eccellente i dati pseudo-sperimentali ottenuti al calcolatore. Grazie al precedente accorgimento, si dispone attualmente di un'equazione che descrive con grande precisione il comportamento di stato di un sistema costituito da sfere dure.

5. Impiego delle funzioni di distribuzione

Le funzioni di distribuzione molecolare specificano la probabilità di trovare alcune serie definite di molecole in particolari posizioni dello spazio. Il loro impiego ha pertanto lo scopo di evidenziare in che modo le forze intermolecolari determinino la struttura di un fluido.

Dato un sistema di N molecole, indichiamo con n₁ (r₁) la probabilità di trovare una di esse nella posizione r₁ indipendentemente da tutte le altre, con n₂ (r₁, r₂) la probabilità di trovare una molecola in r₁ e una in r₂ indipendentemente dalle altre, e così via. In un fluido isotropo vale la relazione

invece, per un fluido costituito da molecole puntiformi prive di interazioni,

È opportuno introdurre le due funzioni seguenti:

Se indichiamo con r la distanza fra le due molecole situate in r₁ e r₂ si può anche scrivere:

h (r) = g (r) - 1. (39)

La g (r), chiamata funzione di distribuzione radiale, moltiplicata per ρ fornisce il valore della densità a una distanza r da una generica molecola presa come riferimento; essa riflette la struttura locale del sistema e ha per i gas, i liquidi e i solidi i tipici andamenti illustrati nella fig. 11. L'importanza di tale funzione si riscontra anche nel fatto che essa ci offre la possibilità di valutare le proprietà termodinamiche dei fluidi. In particolare, nell'ipotesi che valga la (8), la loro energia potenziale si può esprimere come segue:

in accordo con lo schema riportato nella fig. 5. Si può osservare che la relazione precedente è simile alla (15), salvo che per l'introduzione della funzione di distribuzione radiale allo scopo di tenere conto della distribuzione non uniforme delle molecole dovuta alle fluttuazioni di densità che si manifestano alle piccole distanze.

Inoltre si dimostra che la pressione del sistema può essere espressa nella forma:

Quest'ultima relazione ci permette di determinare l'equazione di stato di un fluido impiegando direttamente la funzione di distribuzione radiale, senza utilizzare l'energia libera secondo lo schema della tab. II.

La funzione di distribuzione radiale può essere determinata sperimentalmente operando secondo lo schema illustrato nella fig. 12. Un fascio di raggi X o di neutroni viene collimato, reso monocromatico e quindi diretto sul campione; mediante un rivelatore si misura l'intensità della radiazione diffratta e da questa, mediante un'opportuna normalizzazione, si risale al fattore di struttura S (k), che dipende dal numero d'onda k = 2π/λ della radiazione incidente di lunghezza d'onda λ. La S (k) è legata alla g (r) dalla seguente relazione:

L'integrale al secondo membro non è altro che la trasformata di Fourier della g (r). Invertendo la trasformata si risale quindi alla funzione di distribuzione radiale.

La h (r) viene invece chiamata funzione di correlazione totale e riflette in che misura la densità locale viene influenzata da una molecola che si trova a una distanza r dal punto considerato. Per distanze elevate la h (r) tende ad annullarsi perché sparisce ogni traccia di correlazione e la distribuzione relativa delle molecole risulta del tutto casuale.

La funzione di correlazione totale può essere espressa anche mediante un'equazione integrale proposta nel 1917 da L. S. Ornstein e F. Zernike, utilizzando una funzione di correlazione diretta c (r) che agisce a corto raggio:

dove (r₁, r₂), (r₁, r₃) ... indicano le posizioni di una coppia di punti. La (43) costituisce una relazione di tipo convolutivo, perché per iterazione fornisce una serie di infiniti termini, nella quale non compare la h (r):

dove i numeri indicano le coordinate di particolari molecole. Mediante opportuni diagrammi la h (1, 2) può essere rappresentata attraverso la somma delle catene di interazioni che influenzano la correlazione fra le molecole 1 e 2:

I cerchi bianchi indicano le molecole 1 e 2, i cui differenziali non compaiono negli integrali, e i cerchi neri le altre molecole.

La (44) costituisce un'equazione integrale che può essere trasformata in una relazione algebrica se si impiegano le trasformate di Fourier,

da cui si ottiene

Questa relazione non è però sufficiente per ricavare delle espressioni esplicite per le due funzioni di correlazione h (r) e c (r): è necessario infatti disporre di un'ulteriore relazione, detta ‛di chiusura'. Fra quelle proposte, ricordiamo le seguenti, introdotte con criteri essenzialmente euristici:

HNC (Hypernetted Chain):

c (r) = - βϕ (r) + h (r) - ln [h (r) + 1], (48)

Percus e Yevick:

c (r) = {1 - e^{βϕ (r)}} [h (r) + 1], (49)

dove ϕ (r) indica, al solito, il potenziale intermolecolare. Nella fig. 13 vengono illustrati alcuni andamenti della funzione di correlazione diretta c (r), corrispondenti alle diverse proposte di chiusura precedentemente indicate.

La relazione di Percus e Yevick (v., 1957) risulta più accurata delle altre e per un sistema di sfere rigide permette di ottenere un'espressione analitica della funzione di distribuzione in eccellente accordo con i dati ottenuti mediante simulazione. Da tale funzione di distribuzione, applicando la (41), si ricava la seguente equazione di stato,

che porta a risultati confrontabili con quelli ottenuti dalla menzionata equazione di Carnahan-Starling.

6. Metodi perturbativi.

Il potenziale intermolecolare rappresentato nella fig. 3 presenta una parte ‛dura' corrispondente alle distanze inferiori al minimo, e una parte ‛soffice' che prevale a distanze superiori. Sulla base di questa osservazione, R. W. Zwanzig (v., 1954) ha suggerito che la struttura di un fluido denso sia essenzialmente determinata dalla parte dura dell'interazione, e che la parte soffice eserciti un'azione correttiva di minore rilevanza, dovuta essenzialmente alle forze attrattive. Questa situazione si riscontra in particolare a temperature relativamente elevate, in corrispondenza delle quali l'energia cinetica delle molecole è a sua volta elevata, mentre il parametro β risulta piccolo.

Per formalizzare tale ipotesi è opportuno anzitutto osservare che l'energia libera può essere scomposta nella somma di due contributi:

il primo dei quali, F_K, deriva dall'energia cinetica delle molecole. F_q viene chiamata energia libera configurazionale ed è connessa con l'integrale delle configurazioni (11) dal cui calcolo, come abbiamo visto, emergono gli aspetti più significativi del comportamento di stato dei fluidi.

Ciò premesso, per calcolare F_q è opportuno scindere il potenziale intermolecolare nella somma di due termini, in accordo con l'ipotesi di Zwanzig; l'energia potenziale del sistema si potrà a sua volta scrivere come segue:

Φ = Φ₀ + Φ_p. (52)

Il primo termine corrisponde a un sistema di riferimento, opportunamente scelto, mentre il secondo costituisce un termine perturbativo. Ne consegue:

In sostanza la Q risulta espressa dall'integrale delle configurazioni del sistema di riferimento moltiplicato per il valore medio canonico dell'esponenziale dell'energia perturbativa exp (-βΦ_p), valutato impiegando la funzione di distribuzione del sistema di riferimento.

È opportuno riscrivere la relazione precedente in una forma di più agevole interpretazione e impiego, effettuando uno sviluppo della F_q rispetto al parametro β, il cui valore, come abbiamo visto, sancisce il limite di validità del metodo perturbativo. Si ottiene:

dove F₀ indica l'energia libera del sistema di riferimento, mentre il terzo termine al secondo membro rappresenta il valore medio delle fluttuazioni dell'energia potenziale.

Se, ad esempio, in prima approssimazione si limita lo sviluppo ai primi due termini, è sufficiente addizionare a F₀ il valore medio dell'energia perturbativa, che a sua volta può essere valutato dalla funzione di distribuzione radiale come segue:

in cui g⁰ (r) è la funzione di distribuzione radiale del fluido di riferimento e ϕ_p (r) la parte perturbativa del potenziale intermolecolare.

In sostanza, sulla base della precedente trattazione, se si dispone di un opportuno sistema di riferimento di cui siano ben note le caratteristiche, è relativamente facile calcolare l'energia libera configurazionale di un particolare fluido. La scelta più immediata cade su un sistema costituito da sfere dure le cui caratteristiche, come è stato illustrato nei capitoli precedenti, sono attualmente ben note. Se come primo esempio consideriamo un fluido costituito da molecole il cui potenziale intermolecolare ha la forma mostrata nella fig. 3B, le sfere dure rappresentano ovviamente il più adeguato sistema di riferimento, mentre la ϕ_p (r) è rappresentata dalla coda attrattiva del potenziale stesso, che in base alla teoria di London risulta inversamente proporzionale alla sesta potenza della distanza. Anzitutto, assumiamo per semplicità che le molecole siano uniformemente distribuite nello spazio, per cui la g⁰ (r) si identifica con la funzione a gradino

g⁰ (r) = Θ (r - σ). (56)

È facile dimostrare che seguendo questa impostazione si ricava l'espressione dell'energia libera ottenuta con la teoria di van der Waals, che pertanto costituisce il primo esempio di applicazione di un metodo perturbativo allo studio dei fluidi. L'analisi svolta permette di migliorare tale teoria, se si tiene conto che in realtà anche per un sistema di sfere dure la funzione di distribuzione radiale non è espressa dalla funzione a gradino, ma segue l'andamento illustrato nella fig. 11. Sviluppando tale approccio si ricava un'equazione di stato che ha la seguente struttura:

dove f (η) può essere espressa mediante una delle equazioni di stato precedentemente descritte, ovvero la (34) o la (50), per rappresentare il comportamento di stato di un sistema di sfere dure. Il secondo termine al secondo membro rappresenta invece il contributo perturbativo dovuto alle forze attrattive. La (57) costituisce una generalizzazione dell'equazione di van der Waals, che viene ricuperata se si pone

La trattazione precedente rappresenta comunque un'applicazione semplificata dei metodi perturbativi, sia perché tale è la forma del potenziale intermolecolare, sia perché si è tenuto conto solo del primo termine dello sviluppo in serie dell'energia libera. In realtà la teoria ha avuto ampi sviluppi e per tale scopo sono stati presi in considerazione diversi sistemi di riferimento, costituiti, ad esempio, da corpi duri aventi varie strutture geometriche (dischi, ellissoidi, sigari, ecc.) in modo da simulare con sempre maggiore dettaglio la forma geometrica delle molecole.

Un ulteriore sviluppo riguarda la descrizione delle molecole polari per le quali è stato scelto, ad esempio, un riferimento costituito da molecole apolari interagenti con un potenziale di Lennard-Jones, considerando l'interazione fra i dipoli quale termine perturbativo. L'applicazione alle miscele ha permesso di descrivere con accuratezza il loro diagramma di fase, includendo anche la regione critica, come appare dagli esempi riportati nelle figg. 14 e 15.

In realtà tali indagini hanno messo in rilievo l'importanza dei parametri che caratterizzano il potenziale intermolecolare, ovvero ε e σ per il potenziale di Lennard-Jones, nella descrizione del comportamento dei fluidi e delle loro miscele. In particolare, se essi sono noti per determinati componenti e si vuole descrivere la miscela, è necessario disporre di accurate regole mediante le quali risulti possibile valutarne i valori corrispondenti alle interazioni fra molecole o gruppi molecolari diversi. Solitamente si ricorre alla media aritmetica per le σ e a quella geometrica, opportunamente corretta, per gli ε, anche se esistono regole di ‛mescolamento' più elaborate. Si tratta comunque di un aspetto sul quale sono necessarie ulteriori indagini teoriche, attualmente in corso.

7. Estensione della teoria di van der Waals alle molecole complesse

In accordo con la teoria di van der Waals nella sua forma originale, la funzione di ripartizione di un fluido può essere scritta come segue:

V_f = (V - b) viene chiamato volume libero e rappresenta il volume accessibile al centro di massa di una molecola che si muove nel volume V che confina il fluido. Se si impiega la definizione (31) di frazione di impacchettamento, è facile dimostrare che il volume libero si può riscrivere anche come segue:

V_f = V (1 - 4η), (60)

da cui risulta che V_f tende a zero per η = 0,25.

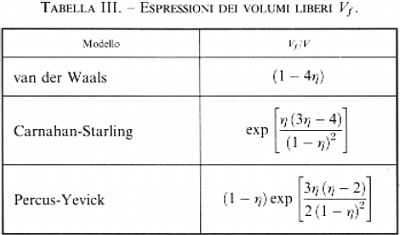
Mediante i metodi perturbativi è stato messo in rilievo come la teoria di van der Waals possa essere migliorata utilizzando delle espressioni che descrivono in modo più accurato il comportamento di stato del fluido di riferimento costituito da sfere dure. Questo risultato si raggiunge anche utilizzando la precedente espressione della funzione di ripartizione, purché si attribuisca a V_f una forma diversa da quella originariamente proposta da van der Waals. Nella tab. III ne vengono riportate alcune, corrispondenti ai modelli di particolari equazioni di stato.

Per poter fare un confronto significativo fra tali espressioni è opportuno prendere come riferimento il volume V₀ = Nσ³/√−2 che corrisponde al massimo impacchettamento che può essere raggiunto da un fluido di sfere dure. Indichiamo inoltre con ρè = ρ/ρ₀ = η/0,74 il rapporto fra la densità del fluido e il suo valore in corrispondenza del massimo impacchettamento, che ovviamente deve essere compreso fra 0 e 1. Nella fig. 16 vengono riportati gli andamenti di V_f/V₀ in funzione di ρ per due dei tre modelli riportati nella tab. III. Si può osservare che mentre il modello Percus-Yevick tende correttamente a zero quando ρè tende all'unità, quello di van der Waals risulta vistosamente inaccurato, poiché la curva di (V_f/V₀) taglia l'ascissa per un valore di ρè pari a 0,338. Tale inaccuratezza si deve attribuire all'arbitrarietà delle ipotesi attraverso le quali è stata formulata la (18).

Ciò premesso si può osservare che nell'ambito del modello precedente le molecole sono in un certo senso assimilate a oggetti interagenti ma privi di struttura, poiché i loro movimenti vibrazionali e rotazionali non vengono influenzati dall'ambiente che circonda le molecole stesse. Pertanto essi sono del tutto indipendenti dal volume del sistema e non determinano la forma dell'equazione di stato. Ovviamente questa ipotesi è rigorosamente vera per i gas monoatomici, come ad esempio l'argon, costituisce un'approssimazione ragionevole per piccole molecole poliatomiche, ma è inadeguata per le molecole di grandi dimensioni, come ad esempio gli idrocarburi con più di 10 atomi di carbonio o, al limite, i polimeri.

Ricordiamo che una molecola costituita da n atomi possiede 3n gradi di libertà, 3 dei quali sono associati ai moti traslazionali e contribuiscono alla funzione di ripartizione con i fattori indicati con Λ. I rimanenti gradi di libertà sono distribuiti fra tre moti rotazionali - che hanno luogo attorno ad assi ortogonali con origine nel centro di massa della molecola - e i moti vibrazionali.

I. Prigogine ha avanzato l'idea che, nel caso delle molecole poliatomiche, il contributo alla Z (V, T, N) dovuto ai moti rotazionali e vibrazionali potesse essere fattorizzato nel prodotto di due termini:

z_r,_v = z_int (T) z_ext (ρ). (61)

Il primo corrisponde ai moti interni nella molecola e pertanto dipende dalla sola temperatura, mentre il secondo corrisponde ai moti esterni e dipende dalla densità. Il numero totale di gradi di libertà esterni verrà indicato con 3c; ovviamente, per le molecole monoatomiche c = 1, mentre per le altre c > 1. In sostanza il parametro c riflette l'entità con cui le rotazioni e le vibrazioni di una molecola risultano influenzate dalla presenza delle molecole a essa vicine e pertanto rappresenta la flessibilità delle molecole.

Per ottenere un'accettabile espressione di z_ext si deve tenere conto che per ogni valore di c devono verificarsi le seguenti condizioni al contorno:

per V → ∞

per V → V₀

dove V₀ è il volume corrispondente a un completo impacchettamento delle molecole. La prima di tali relazioni è necessaria per poter recuperare l'equazione di stato dei gas perfetti quando il volume diviene molto elevato. La seconda riflette invece il fatto che quando le molecole sono impacchettate nel modo più denso possibile tutti i gradi di libertà esterni risultano bloccati, perché la molecola non può esercitare alcun tipo di moto. Si può allora osservare che entrambe le condizioni precedenti risultano soddisfatte se si pone

tenendo presente che al massimo impacchettamento il volume libero deve essere ovviamente nullo.

La sostituzione dell'espressione precedente in quella della funzione di ripartizione permette di sviluppare un modello più generale che viene contraddistinto con l'acronimo PHCT (Perturbed Hard-Chain Theory, ovvero teoria delle catene dure perturbate). Essa fornisce un'equazione di stato che si estende dai fluidi costituiti da molecole semplici a quelli formati da molecole complesse, in un intervallo di densità che va dal gas perfetto ai liquidi con massimo impacchettamento, come illustrato nella fig. 17. Nell'ambito di tale modello, di cui esistono diverse varianti a seconda delle espressioni impiegate per V_f e per l'integrale che esprime l'interazione attrattiva, c viene considerato un parametro semiempirico, ovvero esso deve essere valutato sulla base dei dati sperimentali. Ad esempio, se prendiamo in considerazione gli idrocarburi tale parametro vale 1 per il metano, 1,91 per l'esano e 2,55 per il dodecano, e pertanto aumenta regolarmente con la lunghezza della molecola.

8. Impiego delle funzioni di distribuzione per fluidi con molecole complesse

Nella fig. 18 viene illustrato il ruolo della struttura molecolare sulle funzioni di distribuzione. Viene infatti evidenziato come la funzione di distribuzione radiale si deforma nel passaggio da un fluido monoatomico a un fluido costituito da molecole biatomiche che hanno una distanza di legame uguale a ℓ〈 σ. Nel primo caso i massimi della g (r) sono ben definiti e modulati dal diametro σ delle molecole, mentre nel secondo si manifesta la presenza di un flesso in corrispondenza di una distanza pari alla somma σ + ℓ, dove ℓ  è la distanza interatomica nelle molecole. La situazione diviene ovviamente sempre più complicata all'aumentare della complessità molecolare.

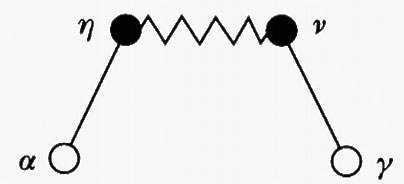
Riferiamoci ora alla fig. 19, nella quale vengono riportate due molecole poliatomiche M ed M′ che interagiscono fra di loro. È opportuno individuare in ciascuna di esse alcuni particolari gruppi o ‛siti' di interazione, indicati rispettivamente con α, η e ν, γ, e con origine nel loro atomo centrale. Si possono allora definire due tipi di funzione di distribuzione radiale,

essendo r la distanza fra i centri interagenti. Queste due funzioni si riferiscono rispettivamente a interazioni corrispondenti a siti che si trovano su molecole diverse e a siti che si trovano sulla stessa molecola.

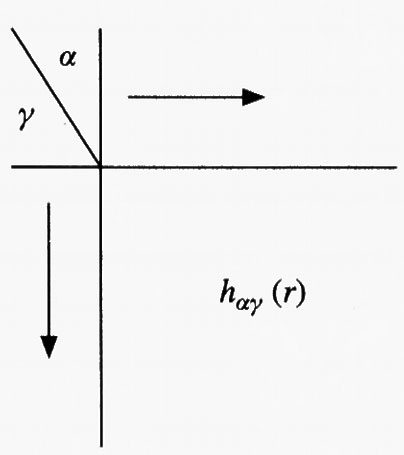
Anche in questo caso si può introdurre una funzione di correlazione totale fra due generici siti α e γ, fra i quali esistono catene di interazioni inter- e intramolecolari del tipo

dove il tratto continuo indica una interazione intramolecolare, mentre quello seghettato si riferisce all'interazione fra siti appartenenti a molecole diverse. Nello schema precedente sono coinvolte due molecole cui appartengono rispettivamente i gruppi γ, ν e α, η.

Ricordiamo ora l'equazione (43), formulata per fluidi semplici. In forma concisa può essere riscritta come segue:

h (r) = c (r) + ρ c * h (r), (65)

dove con l'asterisco si indica il prodotto di convoluzione. La relazione precedente può essere generalizzata a fluidi contenenti molecole poliatomiche riscrivendola nella forma seguente,

h = ω * c * ω + ρ * ω * c * h (66)

h, c e ω indicano delle opportune matrici di correlazione i cui elementi riflettono le diverse interazioni fra i gruppi nei quali sono state scomposte le molecole. Ad esempio, h (r) costituisce la matrice di correlazione totale sito-sito, avente la forma:

Analogamente:

c (r) ≡ ∣C_αγ (r)∣

è la matrice di correlazione diretta sito-sito, mentre

è la matrice di correlazione diretta intramolecolare, dove δ (r) indica la funzione di Dirac.

Grazie alle precedenti definizioni risulta possibile generalizzare l'equazione (43), estendendo la teoria delle funzioni di distribuzione dei fluidi semplici a quelli costituiti da molecole complesse. A tale scopo si scrive:

h (r) = ω * c * ω (r) + ρ * ω * c * h (r), (67)

dove la correlazione complessiva fra due siti viene descritta come se si propagasse attraverso una catena di correlazioni dirette.

Per poter procedere è però necessario valutare gli elementi delle matrici di correlazione diretta. Osserviamo anzitutto che gli elementi delle ω (r), per α = η, e quindi r = 0, sono uguali all'unità. Per α ≠ η, si può invece porre

dove ℓ_αη, è la distanza fra gli atomi centrali α ed η. La relazione precedente esprime essenzialmente il fatto che la funzione di correlazione intramolecolare è rappresentata da un picco che si trova a distanza  ℓ_αη dall'atomo di riferimento, ma localizzato su un generico punto della superficie di una sfera di raggio  ℓ_αη.

Più difficile è la valutazione degli elementi c_αγ (r) della matrice di correlazione diretta intermolecolare. Un modo di procedere è quello di impiegare una funzione di r che simuli l'andamento dell'equazione di Percus-Yevick (49), che, come abbiamo visto, costituisce la migliore chiusura sino ad ora proposta dell'equazione (43) per fluidi semplici. Il metodo ora descritto viene solitamente contraddistinto con la sigla RISM (Reference Interaction Site Model) proposta da D. Chandler (v., 1987).

Una situazione di particolare interesse è quella corrispondente a molecole con un nocciolo duro, assimilabili a una catena di sfere connesse fra di loro, e ciascuna corrispondente a un particolare sito. Il loro studio con il metodo RIMS porta a funzioni di distribuzione ed equazioni di stato corrispondenti a quelle precedentemente descritte per fluidi costituiti da sfere rigide. Dal punto di vista operativo si procede naturalmente utilizzando nell'equazione integrale (67) la trasformata di Fourier, e si giunge a un'equazione matriciale del tipo:

ĥ (k) = ῶ (k) ĉ (k) [1 - ρ ωé (k) cé (k)]^-1 ῶ (k). (69)

Tralasciando i dettagli, riportiamo a scopo illustrativo alcuni dei risultati ottenuti applicando il metodo descritto. Nella fig. 20 vengono mostrate le funzioni di distribuzione radiale calcolate per la molecola simmetrica dell'azoto e per molecole asimmetriche. In entrambi i casi i risultati ottenuti per diverse coppie di atomi sono in ottimo accordo con quelli ricavati dalla simulazione numerica con il metodo Monte Carlo.

Con questo approccio vengono attualmente affrontati problemi concernenti la struttura di liquidi formati da molecole complesse, inclusi i sistemi polimerici.

9. Conclusioni

La trattazione sviluppata nei capitoli precedenti mette in rilievo il ruolo della termodinamica molecolare nelle indagini sulle proprietà di equilibrio dei fluidi. Attraverso le funzioni di distribuzione essa offre inoltre la possibilità di approfondire le caratteristiche strutturali dei liquidi costituiti da molecole complesse. Le ricerche attuali sono infatti in larga misura focalizzate sullo studio dei sistemi polimerici e delle loro miscele, con lo scopo di individuarne i limiti di stabilità, oltre i quali hanno luogo processi di smiscelamento. Un ulteriore sviluppo di tali ricerche riguarda la termodinamica delle interfasi fluido-solido, attraverso l'approfondimento dei processi di adsorbimento. In particolare, l'interesse è volto ai materiali aventi una porosità regolare dovuta a una ben definita configurazione geometrica, quali le zeoliti. Un altro aspetto, che è stato solo sfiorato ma che meriterebbe attenta considerazione, riguarda le regioni critiche e supercritiche. È noto infatti che in prossimità delle temperature critiche relative sia alla fase gas-liquido che allo smiscelamento fra due fasi liquide si manifesta un comportamento peculiare espresso da leggi universali che possono essere individuate mediante la tecnica del ‛gruppo di rinormalizzazione' (v. transizioni di fase, vol. VIII).

Anche la zona immediatamente al di sopra della temperatura critica relativa alla transizione gas-liquido risulta di interesse per la ricaduta che essa può avere relativamente a una particolare tecnologia di estrazione detta ‛supercritica'.

Nella presente trattazione è stata data particolare enfasi all'impiego delle equazioni di stato anche per la descrizione delle miscele, poiché si tratta dell'approccio più moderno e per certi aspetti più efficace per affrontare tali problematiche. In questa impostazione acquistano particolare rilevanza le indagini sulle forze intermolecolari, soprattutto per quanto concerne le interazioni fra molecole diverse, poiché forniscono informazioni essenziali per ogni indagine che si proponga di descrivere le proprietà di equilibrio della materia.

BIBLIOGRAFIA

Balescu, R., Equilibrium and nonequilibrium statistical mechanics, New York 1975.

Barker, J. A., Henderson, D., What is ‟liquid"? Understanding the states of matter, in ‟Reviews of modern physics", 1976, XLVIII, pp. 587-671.

Beret, S., Prausnitz, J. M., Perturbed hard-chain theory, in ‟American Institute of Chemical Engineers journal", 1975, XXI, pp. 1123-1132.

Carnahan, N. F., Starling, K. E., Intermolecular repulsions and the equation of state for fluids, in ‟American Institute of Chemical Engineers journal", 1972, XVIII, pp. 1184-1189.

Carrà, S., Termodinamica, Torino 1990.

Carrà, S., Morbidelli, M., Thermodynamic aspects of multicomponent adsorption processes on zeolites, in ‟International review in physical chemistry", 1987, VI, pp. 351-365.

Chandler, D., Equilibrium theory of polyatomic fluids, in The liquid state of matter: fluids, simple and complex (a cura di E. W. Montroll e J. L. Lebowitz), Amsterdam-New York 1982, pp. 275 ss.

Chandler, D., Introduction to modern statistical mechanics, New York 1987.

Donohue, M. D., Prausnitz, J. M., Perturbed hard-chain theory for fluid mixtures, in ‟American Institute of Chemical Engineers journal", 1978, XXIV, pp. 849-860.

Flory, J. P., Statistical thermodynamics of liquid mixtures, in ‟Journal of the American Chemical Society", 1965, LXXXVII, pp. 1834-1838.

Green, H. S., The molecular theory of fluids, Minneola, N. Y., 1969.

Hildebrand, J. H., Scott, R. L., The solubility of nonelectrolytes, Minneola, N. Y., 1950.

Hirschfelder, J. O., Curtiss, C. F., Bird, R. B., Molecular theory of gases and liquids, New York 1954.

Kac, M., Uhlenbeck, G. E., Hemmer, P. C., On the van der Waals theory of the vapor-liquid equilibrium, in ‟Journal of mathematical physics", 1963, IV, pp. 216-247.

Lifshitz, I. M., Grosberg, A. Y., Khokhlov, A. R., Some problems of the statistical physics of polymer chains with volume interaction, in ‟Reviews of modern physics", 1978, L, pp. 683-713.

Mayer, J. E., Göpper Mayer, M., Statistical mechanics, New York 1940.

Morbidelli, M., Carrà, S., Employment of vapor-pressure data in the description of vapor-liquid equilibrium with direct method, in ‟American Institute of Chemical Engineers journal", 1981, XXVII, pp. 673-679.

Percus, J. K., Yevick, G. J., Analysis of classical statistical mechanics by means of collective coordinates, in ‟Physical review", 1957, CX, pp. 1-13.

Prausnitz, J. M., Lichtenthaler, R. N., Azevedo, E. G. de, Molecular thermodynamics of fluid-phase equilibria, Englewood Cliffs, N. J., 1986.

Reed, T. M., Gubbins, K. E., Applied statistical mechanics: thermodynamic and transport properties of fluids, New York 1973.

Rowlinson, J. S., Liquids and liquid mixtures, London 1969².

Rushbrooke, G. S., Equilibrium theories of the liquid state, in Physics of simple liquids (a cura di H. V. N. Temperley, J. S. Rowlinson e G. S. Rushbrooke), Amsterdam 1968, pp. 26-58.

Sandler, S. I., The generalized van der Waals partition function. I. Basic theory, in ‟Fluid phase equilibria", 1985, XIX, pp. 233-257.

Soave, G., Equilibrium constants from a modified Redlich-Kwong equation of state, in ‟Chemical engineering science", 1972, XXVII, pp. 1197-1203.

Vera, J. H., Prausnitz, J. M., Generalized van der Waals theory for dense fluids, in ‟Chemical engineering journal", 1972, III, pp. 1-13.

Whalen, J. W., Molecular thermodynamics: a statistical approach, New York 1991.

Zwanzig, R. W., High-temperature equation of state by a perturbation method, in ‟Journal of chemical physics", 1954, XXII, pp. 1420-1426.