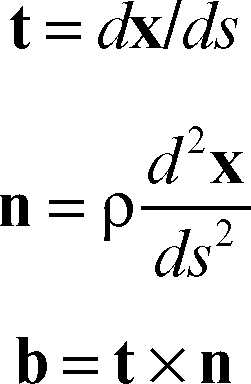terna intrinseca

terna intrinseca

terna intrinseca in geometria, relativamente a una curva dello spazio assegnata mediante equazioni parametriche e assumendo come parametro la sua ascissa curvilinea s, è la terna costituita dal versore tangente t (parallelo alla retta tangente al sostegno della curva nel punto geometrico considerato), dal versore normale n (che individua la normale principale alla curva in quel punto) e dal versore binormale b della curva in quel punto (perpendicolare ai precedenti). Essi sono così definiti

dove ρ è il raggio di curvatura e × indica il prodotto vettoriale. I tre vettori, associati a ogni punto in cui la curva sia differenziabile due volte, dipendono dall’ascissa curvilinea s e forniscono rispettivamente la direzione della curva in quel punto, la sua flessione (o prima curvatura) e la sua torsione (o seconda curvatura). Il piano individuato dai versori tangente e normale è il piano osculatore della curva, il piano individuato dai versori tangente e binormale è detto piano rettificante, mentre il piano individuato dai versori normale e binormale è il piano normale alla curva (→ Frenet, formule di). La terna {t, n, b} è detta triedro di Frenet (oppure anche triedro fondamentale o principale): è una base ortonormale, descrive localmente la curva ed è utile nello studio del moto di un punto materiale vincolato a muoversi lungo tale curva.