test

test

Procedura per determinare se una particolare ipotesi statistica (➔) sia o meno consistente con l’evidenza empirica (➔ anche stimatore), anche chiamata ipotesi nulla e indicata con H₀. L’obiettivo finale della procedura è quello di decidere se rifiutare o meno H₀.

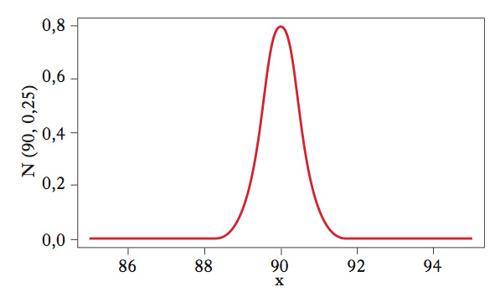
Ipotesi nulla e regione di rifiuto

Oltre all’ipotesi nulla si può specificare anche un’ipotesi alternativa, H₁, che descrive quale particolare insieme di deviazioni dalla prima sia rilevante per l’analisi. Un t. dell’ipotesi nulla H₀ è costituito da 3 elementi. Una statistica T, chiamata statistica test (➔ statistica); una partizione dell’insieme dei possibili valori di T in due regioni: la regione R di valori che non sono in accordo con l’ipotesi nulla, chiamata regione di rifiuto, e il suo complemento, o regione (intervallo) di non rifiuto (➔ rifiuto, intervallo di); una regola decisionale che rifiuta l’ipotesi nulla se il valore osservato di T cade nella regione R e non rifiuta in caso contrario. Il complemento della regione di rifiuto è a volte chiamata regione di accettazione. Si tratta però di una terminologia impropria e fuorviante: come ricorda K.R. Popper, il fatto di non rifiutare l’ipotesi nulla non significa in generale che questa sia vera. Per illustrare un t. statistico, si prenda in considerazione un’ipotesi sulla media di una popolazione con varianza nota. Si consideri specificatamente l’ipotesi che la percentuale di promossi nelle prime classi delle scuole superiori sia del 90%. L’ipotesi nulla si scrive quindi H₀:μ=90. Un’ipotesi di questo tipo, che specifica un unico valore per il parametro di interesse, è chiamata ipotesi semplice. La naturale alternativa a questa è l’ipotesi bidirezionale H₁:μ≠90, anche se sono possibili alternative diverse. Si supponga di osservare la percentuale di studenti promossi in un campione di 32 scuole ottenendo la media campionaria x̄=89. Se la popolazione ha distribuzione gaussiana (➔ gaussiana, distribuzione) di varianza nota σ²=8, allora, sotto l’ipotesi nulla (cioè se l’ipotesi nulla è vera), la statistica X̄ ha una distribuzione gaussiana di media μ=90 e varianza σ²/32=1/4. Di conseguenza, sotto l’ipotesi nulla, l’insieme di valori di X̄ meno verosimili sono quelli più lontani dalla media μ=90 poiché a essi corrisponde una probabilità più bassa di essere osservati. La regione di rifiuto è quindi l’insieme dei valori di X̄ per i quali la distanza ∣X̄−90∣ supera una soglia prefissata, cioè R={X̄:∣X̄−90∣>c}. La soglia c è chiamata valore critico del test. A valori critici diversi corrispondono regioni di rifiuto diverse.

Probabilità di errore

Quando si effettua un t. statistico c’è sempre la possibilità di commettere un errore rifiutando un’ipotesi nulla vera (errore di prima specie), oppure non rifiutando un’ipotesi nulla falsa (errore di seconda specie). Per es., per puro effetto del caso, potrebbero essere state selezionate 32 scuole con una percentuale eccezionalmente bassa di promossi. Un criterio per scegliere la regione di rifiuto di un t. è quello di fissare la probabilità di errore di prima specie a un livello dato α. Scelto α, detto anche livello di significatività o semplicemente livello del t., si determina il valore critico c risolvendo l’equazione P(X̄∈R∣H₀ è vera)=P(∣X̄−90∣>c=α). Valori tipici per α sono α=0,1; 0,05; 0,025; 0,01. Aumentando c diminuisce la probabilità di errore di prima specie, ma cresce quella di seconda specie, poiché si riduce l’area della regione di rifiuto. La regione complementare a R, cioè R^c={X̄:∣X̄−90∣≤c}, è un intervallo di confidenza (➔ confidenza, intervallo di) al livello di copertura 1−α, dove α è il livello di significatività del test. Un approccio diverso, che ribalta la logica nella definizione della regione di rifiuto (pur portando allo stesso risultato) è basato sul calcolo del p-value, o valore p. Invece di calcolare il valore critico, si calcola il livello di significatività del t. con valore critico c=∣x̄−μ∣, dove  è il valore osservato (nell’esempio, c=∣89−90∣=1). La probabilità corrispondente è il p-value p. Si rifiuta l’ipotesi nulla se il p-value è inferiore al livello di significatività α. In entrambi gli approcci, per calcolare la regione di rifiuto è necessario conoscere la distribuzione di probabilità della statistica test sotto l’ipotesi nulla (nell’esempio X̄ è normale con media 90 e varianza 1/4). Quando questo non sia possibile, si possono cercare approssimazioni basate sulla distribuzione asintotica della statistica test (➔ asintotica, distribuzione), oppure usare altri metodi come il bootstrap (➔ bootstrap, metodo). La probabilità di rifiutare correttamente l’ipotesi nulla è chiamata potenza del test. È generalmente indicata con β e si ha quindi che 1−β è la probabilità di errore di seconda specie. La potenza del t. è usata per il confronto tra due t. di pari significatività (➔ efficienza statistica). Si possono anche sottoporre a verifica ipotesi nulle più complesse, dette ipotesi composite, che non sono limitate a un unico valore del parametro. Talvolta, inoltre, le ipotesi possono riguardare più parametri. Se nel caso di un’unica ipotesi la regione di non rifiuto è tipicamente un intervallo, nel caso di ipotesi multiple la regione di non rifiuto è un insieme multidimensionale.

Test parametrici e non parametrici

I t. possono essere parametrici, cioè basati su un modello parametrico, o non parametrici. Tra i t. del primo tipo si ricordano il t. T (➔ T, test), il t. F (➔ F, test), il t. del chi-quadro (➔ chi quadro, test), e i test basati sulla funzione di verosimiglianza (➔). Tra i t. non parametrici vanno menzionati quelli detti distribution free, cioè tali che la distribuzione di probabilità della statistica t. (sotto l’ipotesi nulla) sia indipendente dalla distribuzione della popolazione, come il t. di Kolmogorov-Smirnov (➔ adattamento, test di), il t. dei ranghi di Wilcoxon, e il t. di Wald-Wolfowitz.