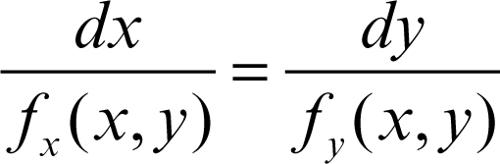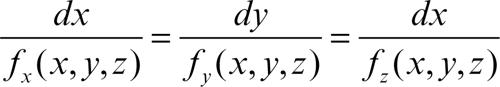traiettoria ortogonale
traiettoria ortogonale
traiettoria ortogonale in analisi, per una famiglia di linee piane F, linea Г che interseca ortogonalmente le linee di F. Per esempio, le traiettorie ortogonali della famiglia di parabole di equazione y 2 − cx = 0 sono date dalle ellissi appartenenti alla famiglia di equazione x 2 + y 2/2 – c = 0 e inoltre dalla retta di equazione y = 0. Se le linee di F sono le linee di livello di una funzione ƒ, e sono quindi descritte dalle equazioni implicite ƒ(x, y) = C, la linea Г è soluzione dell’equazione differenziale
che esprime il parallelismo tra la tangente a Г e la normale alla linea ƒ = C, individuata dal → gradiente di ƒ. Per esempio, le traiettorie ortogonali alla famiglia di iperboli x 2 − y 2 = C sono le iperboli della famiglia xy = k. Analogamente, nello spazio la linea Г si chiama traiettoria ortogonale alle superfici della famiglia ƒ(x, y, z) = C se soddisfa il sistema differenziale
Tipico è il caso delle linee di forza di un vettore conservativo, che sono ortogonali alle linee (superfici) equipotenziali.