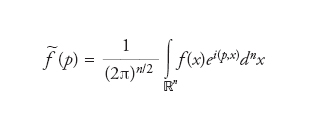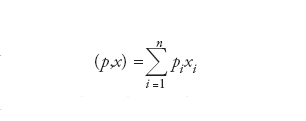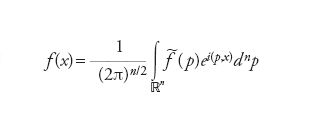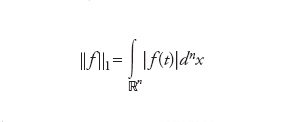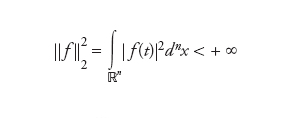trasformata di Fourier

trasformata di Fourier

Una trasformazione integrale che mappa una funzione a valori complessi f(x):ℝⁿ→ℂ nella sua corrispondente trasformata di Fourier (detta anche funzione spettrale o dai fisici spettro di frequenza) f ∼(p):ℝⁿ→ℂ, definita dall’integrale di Fourier

formula

dove

[2] formula

indica l’usuale prodotto scalare in ℝⁿ. La trasformata di Fourier ammette un’operazione inversa, ovvero

[3] formula.

Condizione sufficiente per l’esistenza della trasformata di Fourier di una funzione f(x) (ossia perché l’espressione in [1] abbia significato) è l’esistenza dell’integrale

[4] formula.

È questa la norma dello spazio di Banach L¹(ℝⁿ,ℂ) delle funzioni sommabili su ℝⁿ; non è difficile dimostrare che per f(x) sommabile la funzione f∼(p) è almeno continua e ∣∣ff∼(p)∣∣_∞=sup∣f∼(p)∣≤∣∣f∣∣₁. Per questa ragione (ricordando le proprietà di additività dell’integrale) la trasformata di Fourier può essere vista come operatore lineare continuo da L¹(ℝⁿ,ℂ) a C(ℝⁿ,ℂ). L’esistenza dell’inversa (ossia dell’integrale [3]) non è però garantita poiché la funzione ff∼(p) non è necessariamente sommabile. Anche nel caso

[5] formula

l’integrale in [1] esiste, ma inoltre ∣∣f∼(p)∣∣₂=∣∣f(x)∣∣₂: la trasformata di Fourier definisce un operatore lineare isometrico (e dunque sempre invertibile) dello spazio di Hilbert L²(ℝⁿ,ℂ) delle funzioni a quadrato sommabile in sé. Dalla definizione è immediato verificare che la trasformata di Fourier di una funzione (sommabile) ha alcune caratteristiche: (a) se f(x) ha valori reali allora f∼(p)=f∼(−p); (b) se f(x) ha valori immaginari f∼(p)=−f∼(−p); (c) (∂f/∂x_i)=P_i f∼(p) (se le derivate parziali esistono). Quest’ultima proprietà è di fondamentale importanza teorica e pratica. Da un lato essa ci dice (sotto opportune ipotesi) che più una funzione è liscia (derivabile) più velocemente la sua trasformata di Fourier si avvicinerà a zero quando ∣∣x∣∣→±∞, dall’altro è chiaro che permette di trasformare equazioni differenziali per funzioni in equazioni algebriche per le loro trasformate di Fourier. È possibile estendere la trasformata di Fourier anche a funzioni generalizzate (distribuzioni) e caratterizzare queste ultime proprio per mezzo della velocità con cui le loro trasformate divergono quando ∣∣x∣∣→±∞. Una tecnica questa che si è rivelata essenziale anche in fisica, dove la trasformata di Fourier descrive la trasformazione tra impulsi e posizione.

→ Liquidi; Stocastica