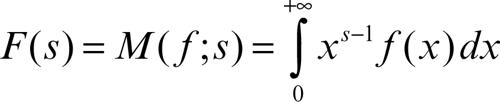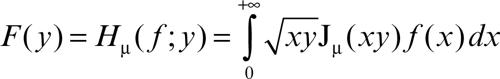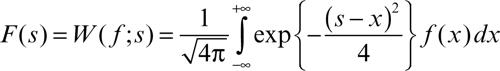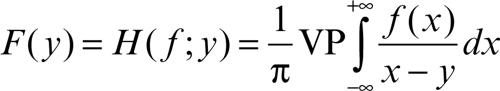trasformata integrale
trasformata integrale
trasformata integrale tecnica di soluzione per equazioni differenziali lineari, sovente alle derivate parziali; si basa su un cambiamento di incognita dato da un integrale definito contenente un parametro, che diviene la nuova variabile indipendente. Le due trasformate più famose sono quelle ottenute con la trasformazione di → Fourier e con la trasformazione di → Laplace, ma molte altre sono state introdotte per affrontare altri casi, differenti per geometria e condizioni al contorno. Per tutte queste trasformazioni esiste una teoria classica, in cui le funzioni si suppongono regolari e integrabili (in senso generalizzato), e una teoria moderna, in cui si opera con funzioni in opportuni spazi funzionali, del tipo spazi di → Sobolev o spazi di distribuzioni (per esempio, contenenti la δ di → Dirac; si veda → distribuzioni, teoria delle). Non si entrerà qui nei dettagli, ma ci si limiterà a dare formule generali, senza indicare le relative ipotesi.
La struttura generale comune a tutte le trasformate integrali è la seguente: sono dati due intervalli I e J (limitati o illimitati) e un nucleo K: I × J → R; la trasformata F(y) = T(ƒ, y) della funzione ƒ: I → R è allora data dall’integrale
e risulta una funzione J → R (non necessariamente definita su tutto J; in alcuni casi le funzioni e le trasformate sono a valori in C). La trasformazione è sempre un operatore lineare; caso per caso, mediante integrazione per parti, si stabiliscono regole per la trasformata della derivata o per il prodotto di ƒ(x) per alcune classi di funzioni, come le potenze xn, gli esponenziali o altre. Essenziale è la possibilità di avere una formula di inversione, che permetta di tornare dalla F alla ƒ, usualmente nella forma
con K−1nucleo di inversione. Molto utili si rivelano formule per trattare i prodotti di → convoluzione, o generalizzazioni del teorema di Plancherel (→ Fourier, trasformazione di). Per le applicazioni pratiche esistono poi tavole più o meno ampie delle trasformate delle principali funzioni (si vedano le tavole delle trasformazioni delle principali funzioni).
Le principali trasformate integrali, oltre alle già citate trasformate di Fourier (con le varianti trasformata seno e coseno) e di Laplace (con la variante bilatera) sono:
• la trasformata di Mellin
utile per lo studio di equazioni che si riducono all’equazione di → Eulero, e in particolare per l’equazione di → Laplace in domini a forma di angolo; il nome deriva da quello del matematico finlandese R.H. Mellin;
• la trasformata di Hankel di ordine reale µ
in cui Jµ è la funzione di → Bessel di prima specie e ordine µ. Essa è impiegata per risolvere equazioni differenziali alle derivate parziali in coordinate cilindriche. Esistono varianti di questa trasformata che fanno uso delle cosiddette funzioni di Bessel modificate; il nome deriva da quello del matematico tedesco H. Hankel; questa trasformata è anche riportata in letteratura come trasformata di Fourier-Bessel;
• la trasformata di Weierstrass
impiegata per lo studio di problemi relativi all’equazione del → calore.
Una classe particolare di trasformate integrali è data dalle cosiddette trasformate di convoluzione, in cui il nucleo ha la forma K(x, y) = G(y − x), e quindi la trasformazione corrisponde al prodotto di convoluzione G ∗ ƒ. Tra queste, un posto significativo ha la trasformata di Hilbert, definita da
dove il simbolo VP indica il valore principale dell’integrale (→ integrale, valore principale di Cauchy di un).
In senso lato, possono essere considerate trasformate integrali anche le successioni dei coefficienti di Fourier generalizzati di una funzione: la variabile y assume per esse valori interi e la formula di inversione, invece di essere data da un integrale, è rappresentata da una serie (→ Fourier, serie di).