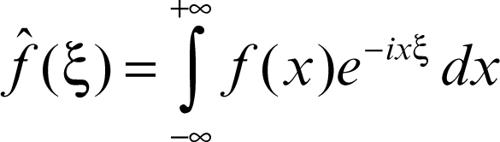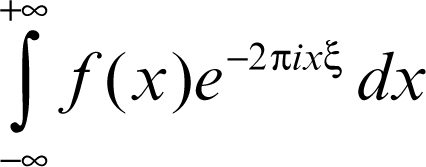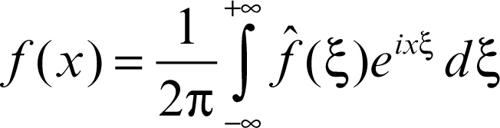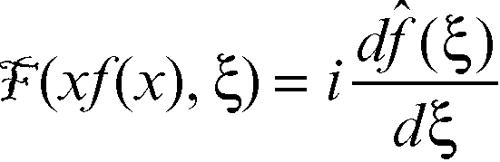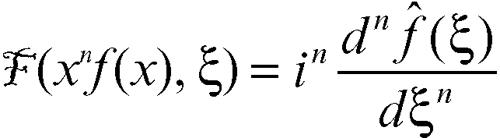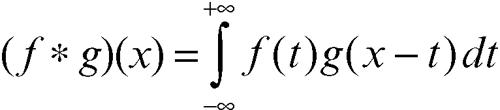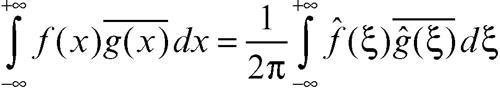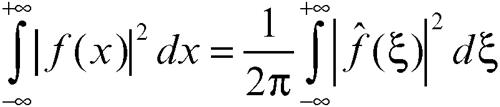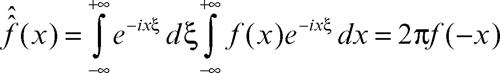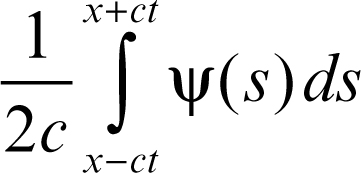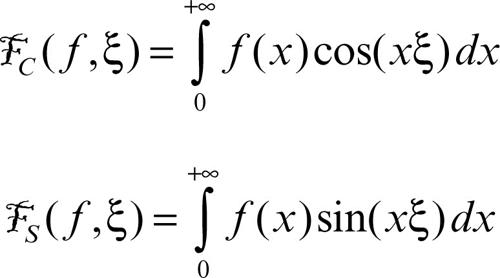Fourier, trasformazione di

Fourier, trasformazione di

Fourier, trasformazione di relazione corrispondente allo sviluppo in serie di Fourier nel caso di funzione non periodica definita su tutto R. Si supponga innanzitutto che la funzione ƒ appartenga a L¹(R). La sua corrispondente nella trasformazione di Fourier, detta trasformata di Fourier di ƒ, è definita dall’integrale

Talvolta la trasformata di Fourier è definita utilizzando delle normalizzazioni mediante

o

che rendono le formule più simmetriche. La definizione tradizionale è tuttavia la più usata nelle applicazioni.

Anche la notazione ha diverse varianti: la più comune è

quanto alle lettere (ovviamente ininfluenti dal punto di vista matematico perché si tratta di corrispondenze tra funzioni e una funzione non dipende dal nome assegnato alla variabile indipendente), si usano spesso λ al posto di ξ (preferibile invece perché corrispondente greco di x) e, nelle applicazioni della teoria dei segnali, t (tempo) al posto di x e ω (pulsazione) al posto di ξ; talvolta si utilizza addirittura j per indicare l’unità immaginaria. Si noti peraltro che nella notazione

la

è lettera specifica per indicare la trasformazione di Fourier, mentre la dipendenza funzionale da ƒ deve essere resa esplicita: anzi, sarebbe più corretto scrivere

non essendo la lettera x in alcun modo significativa; mentre scrivendo

la lettera ƒ che designa la funzione viene mantenuta, indicandosi la trasformazione col segno di circonflesso. La funzione

risulta continua e infinitesima per ξ tendente a ±∞ (→ Riemann-Lebesgue, lemma di). Nota la trasformata, è possibile calcolare la funzione ƒ mediante la formula di inversione

dove l’integrale va inteso nel senso del valore principale (→ integrale, valore principale di un) e l’uguaglianza vale sotto le stesse ipotesi dei teoremi sulle serie di Fourier.

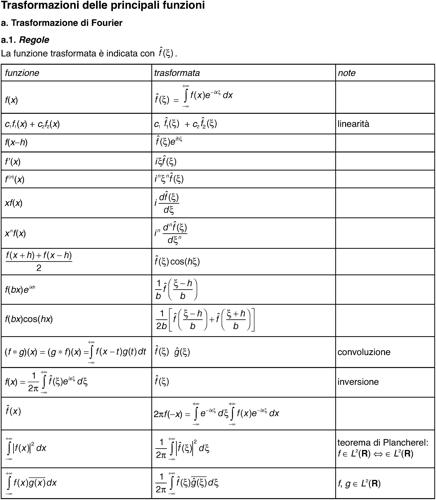
Valgono inoltre le seguenti proprietà:

e, in generale,

e, in generale,

dove la convoluzione (f ∗ g)(x) delle due funzioni f e g è definita dall'integrale

e, in particolare,

(→ Plancherel, teorema di)

(se tali integrali esistono).

Le formule d) ed e) valgono rispettivamente sotto l’ipotesi supplementare che anche le funzioni ƒ ⁽ⁿ⁾(x) e xⁿƒ(x) ∈ L¹(R). Da esse si deduce che quanto più è regolare la funzione ƒ, tanto maggiore è l’ordine di infinitesimo di f̂, e, viceversa, quanto più è alto l’ordine di infinitesimo di ƒ, tanto più regolare è f̂. Il teorema di Plancherel, indicato come proprietà g) e valido se le due funzioni ƒ e g ∈ L²(R), mostra invece che la trasformata di Fourier (a meno del fattore 1/(2π)) è una isometria tra L² e L²; poiché L¹ ∩ L² è denso in L², si può così estendere la definizione di trasformata di Fourier a tutto L²(R). In tal caso però viene a cadere il lemma di Riemann-Lebesgue, non essendo le funzioni di L² in genere né continue né infinitesime per x → ∞. Un altro caso in cui i due spazi, delle funzioni e delle loro trasformate, coincidono è quello delle funzioni a decrescenza rapida (→ distribuzione).

Tra le applicazioni della trasformata di Fourier è di primaria importanza lo studio delle equazioni differenziali lineari alle derivate parziali: infatti, la formula d) consente di ridurre una derivazione al prodotto per una variabile e quindi di ridurre il numero di variabili rispetto a cui l’incognita è derivata.

Per esempio, se si studia il problema di Cauchy u(x, 0) = φ(x), u_t(x, 0) = ψ(x) per l’equazione della corda vibrante di lunghezza infinita u_tt = c²u_xx, si può calcolare la trasformata di Fourier dell’incognita u, considerando t come parametro. Posto dunque

si avrà

mentre per la d)

L’equazione

è ora un’equazione differenziale ordinaria, a coefficienti costanti, per cui la soluzione del problema di Cauchy, che si trasforma a sua volta in

è esplicitamente calcolabile, e risulta:

Il primo addendo, trasformando il coseno in (e^ictξ + e^−ictξ)/2 mediante le formule di Eulero e utilizzando la b), risulta la trasformata di [φ(x − ct) + φ(x + ct)]/2. Per il secondo addendo si può notare che sin(cξt)/(cξ) è uguale a

con χ funzione caratteristica dell’intervallo [−ct, ct] e ottenere che esso è la trasformata della convoluzione di tale funzione con il dato iniziale ψ(x), e quindi dell’integrale

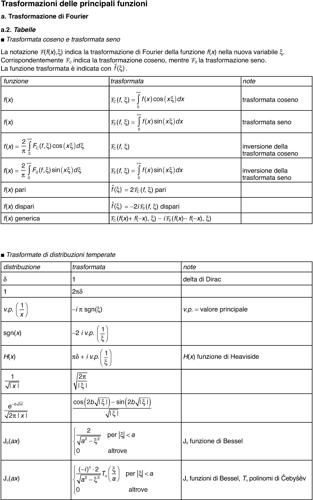
Nelle applicazioni si utilizzano frequentemente anche le cosiddette trasformata coseno e trasformata seno di Fourier. Esse sono definite rispettivamente dagli integrali:

Grazie alla formula di Eulero si verifica subito che se ƒ(x) è una funzione pari su R, allora risulta

mentre se ƒ è dispari si ha

potendosi nel caso generale scrivere:

Nelle applicazioni dunque, l’uso delle trasformate coseno e seno ha il vantaggio di evitare sempre il campo complesso (si vedano le tavole delle trasformate delle principali funzioni).