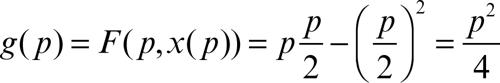Legendre, trasformazione di
Legendre, trasformazione di
Legendre, trasformazione di trasformazione che associa a una data funzione una nuova funzione che ha come argomento la derivata della funzione iniziale. Si considerino una funzione ƒ(x) convessa e un numero p. Introdotta la funzione F(p, x) = px − ƒ(x), che rappresenta, a meno del segno, la distanza verticale tra il grafico di ƒ(x) e la retta per l’origine di coefficiente angolare p, si identifica per ogni valore di p il punto x(p) per il quale la F ha un massimo. La convessità di ƒ(x) assicura che, se tale punto esiste, è unico. Si definisce trasformata di Legendre della ƒ(x) la funzione g(p) = F(p, x(p)). La condizione su x(p) corrisponde alla condizione
ossia p = ƒ′ (x). Se per un certo valore di p non esiste alcun valore di x che sia un massimo di F, allora quel valore di p è al di fuori del dominio della funzione trasformata g(p). Per effettuare operativamente la trasformazione, dopo aver trovato la derivata della funzione, la si inverte in modo da esprimere x come funzione di ƒ′ (x) e si sostituisce tale valore in F. Per esempio, sia ƒ(x) = x 2, allora p = 2x da cui x(p) = p/2, che sostituito nella F fornisce la funzione trasformata:
La trasformata di Legendre è un’involuzione, ossia applicata due volte da l’identità. Inoltre se g(p) e ƒ(x) sono l’una la trasformata di Legendre dell’altra, sussiste la disuguaglianza ƒ(x) + g(p) ≥ xp, detta disuguaglianza di Young, dal nome del matematico inglese W.H. Young.
La trasformata di Legendre in n variabili è definita in modo del tutto analogo, sostituendo però a x e p due vettori x = (x1, x2, …, xn) e p = (p1, p2, …, pn). La funzione trasformata è g(p) = maxx[(x, p) − ƒ(x)], dove (x, p) indica il loro prodotto scalare e
Una funzione di n variabili può anche essere trasformata parzialmente limitando l’operazione sopra descritta a un sottoinsieme di m variabili e ottenendo una funzione trasformata il cui argomento è il vettore di componenti (p1, p2, …, pm, xm+1, …, xn).
In meccanica analitica, la trasformata di Legendre parziale consente di passare dalla funzione → lagrangiana alla funzione → hamiltoniana
limitando la trasformazione alle variabili (le derivate rispetto al tempo delle coordinate) e scrivendole come funzione delle variabili p (i momenti coniugati delle coordinate). La trasformata di Legendre è anche usata in termodinamica per ottenere, a partire dall’energia interna, gli altri potenziali termodinamici: l’entalpia, l’energia libera e l’energia di Gibbs.