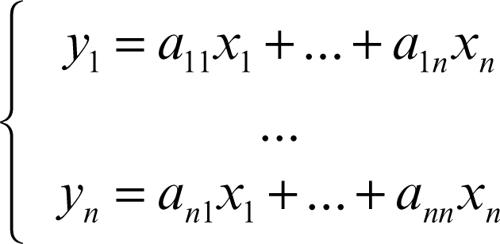trasformazione lineare

trasformazione lineare

trasformazione lineare in algebra lineare, altra locuzione per → applicazione lineare, cioè applicazione ƒ tra due spazi vettoriali V e W su un campo K tale che per ogni coppia di elementi λ, μ appartenenti a K e per ogni coppia di vettori v₁, v₂ ∈ V risulta ƒ(λv_i + μv₂) = λƒ(v₁) + μƒ(v₂). La trasformazione si dice trasformazione lineare invertibile se è un isomorfismo; se W coincide con V è un automorfismo. Se V è uno spazio vettoriale di dimensione finita n, se {e₁, …, e_n} è una sua base, se (x₁, …, x_n) sono le coordinate di un arbitrario vettore x di V e (y₁, …, y_n) sono le coordinate del vettore y = ƒ(x), allora le coordinate di y sono espresse da

o, equivalentemente, in forma matriciale y = Ax, in cui la matrice

è detta matrice della trasformazione lineare nella base {e₁, …, e_n} ed è non singolare (cioè tale che det(A) ≠ 0, e quindi invertibile) se e solo se la trasformazione lineare è invertibile; la sua matrice inversa A⁻¹ è la matrice della trasformazione inversa ƒ ⁻¹ L’insieme stesso di tali matrici quadrate di ordine n su un campo forma un gruppo rispetto all’operazione di prodotto righe per colonne, detto gruppo lineare generale di ordine n su K (→ gruppi classici). Se K è il campo dei numeri reali, si ha il gruppo ortogonale reale se la matrice A è ortogonale (AA^T = A^TA = I); il gruppo speciale ortogonale reale (gruppo delle rotazioni) se il determinante di A è uguale a 1 (le trasformazioni ortogonali con determinante uguale a −1 sono dette simmetrie e non formano un gruppo); se A è una matrice di permutazione si ha il gruppo simmetrico di grado n e il relativo sottogruppo delle permutazioni di classe pari è detto gruppo alterno.