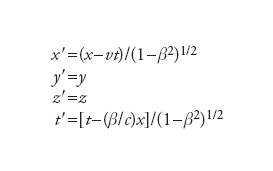trasformazioni di Lorentz

trasformazioni di Lorentz

Trasformazioni lineari delle coordinate nello spazio-tempo di Minkowski che lasciano inalterata la distanza tra due eventi. Indicando con x,y,z,t e con x′,y′,z′,t′ rispettivamente le coordinate di due eventi, esse si possono scrivere nel seguente modo:

dove β=v/c. Affinché le trasformazioni siano reali, deve valere la condizione β≤1, cioè v≤c: in altri termini, la velocità di un corpo (rispetto a un qualsiasi riferimento galileiano) non può mai superare la velocità della luce. Dalle trasformazioni di Lorentz si deducono, nell’ambito cinematico, tre fatti fondamentali: la relatività della contemporaneità, la contrazione delle lunghezze (o contrazione di Lorentz), la dilatazione dei tempi. La relatività della contemporaneità si esprime nel seguente modo: due eventi risultano contemporanei rispetto a due osservatori che si muovano l’uno rispetto all’altro di moto traslatorio rettilineo uniforme soltanto se i due eventi si verificano nello stesso posto. La contrazione delle lunghezze consiste nel fatto che la lunghezza di un segmento valutata da un osservatore che sia in moto rispetto a essa risulta minore di quella che misurerebbe un osservatore in quiete rispetto al segmento. Precisamente, se AB è un segmento fisso rispetto all’osservatore O ed l ne è la lunghezza misurata da O, la sua lunghezza l′ misurata da O′ vale l′=l(1−β²)^1/2〈l. Un treno in corsa, per es., ha per un osservatore a terra lunghezza minore di quella che gli attribuisce un osservatore che si trovi sul treno. Questo effetto non è apprezzabile alle velocità ordinarie, cioè molto inferiori alla velocità della luce. La durata di un fenomeno misurata da un osservatore in moto risulta invece maggiore di quella misurata da un osservatore in quiete (dilatazione dei tempi): indicando con ∆t′ e ∆t le due durate, si ha ∆t′=∆t(1−β²)^1/2.

→ Astrofisica delle alte energie