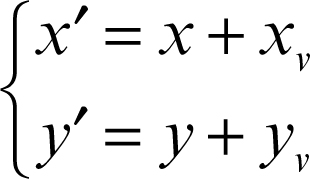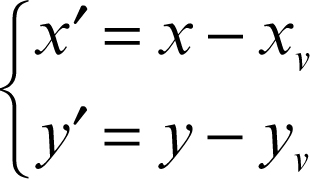traslazione

traslazione

traslazione corrispondenza biunivoca in sé della retta, del piano o dello spazio che a ogni punto P associa un punto P' tale che la direzione. il verso e la lunghezza del segmento orientato

risultino costanti. Informalmente, una traslazione è un movimento rigido che “sposta” tutti i punti di uno stesso tratto, nella stessa direzione e nello stesso verso. Dal punto di vista formale, la traslazione è definita come la trasformazione che, fissato un vettore v, associa a ogni punto P il punto P' = P + v. La traslazione è una isometria diretta; se v ≠ 0, è priva di punti uniti, altrimenti coincide con l’identità e tutti i punti risultano uniti. Il prodotto di due traslazioni è una traslazione avente per vettore la somma dei vettori delle traslazioni componenti. Le traslazioni del piano formano un → gruppo abeliano rispetto all’operazione di composizione di trasformazioni e formano anche uno spazio vettoriale bidimensionale su R, isomorfo a R². Una traslazione può essere considerata come caso limite di una rotazione il cui centro è all’infinito.

Nel piano, riferito a un riferimento cartesiano Oxy, una traslazione di vettore v = (x_v, y_v) ha equazioni:

dove (x, y) e (x', y' ) sono, rispettivamente, le coordinate di P e del suo trasformato P' rispetto allo stesso riferimento Oxy.

Se per esempio nel piano si effettua una traslazione di vettore v(1, 3), le coordinate del punto P' corrispondente del punto P(x, y), sempre in rapporto al riferimento Oxy, sono P' (x + 1, y + 3).

Se anziché una trasformazione dei punti del piano, si effettua una traslazione degli assi del riferimento cartesiano Oxy di vettore v = (x_v, y_v), le coordinate di un punto P(x, y) nel nuovo riferimento Ox'y' sono:

Pertanto, in una traslazione degli assi del riferimento Oxy di vettore v(1, 3), il punto P, nel nuovo riferimento traslato rispetto a Oxy, ha coordinate P(x − 1, y − 3).