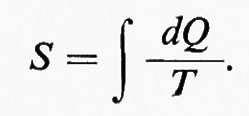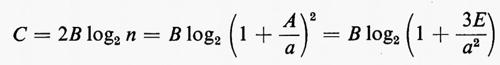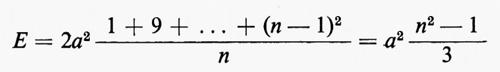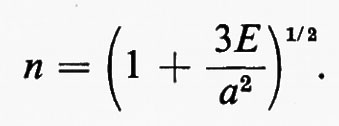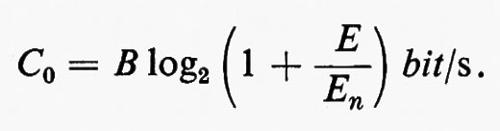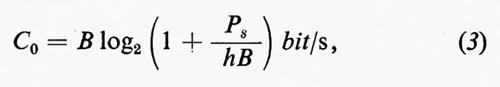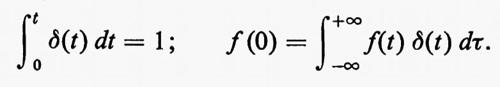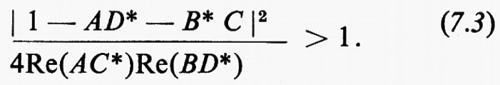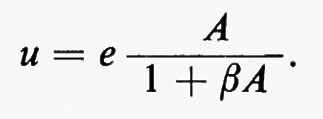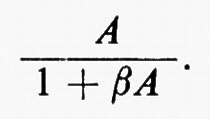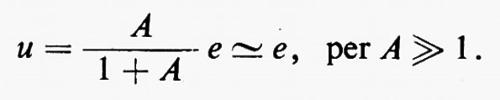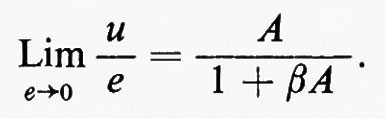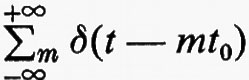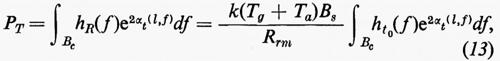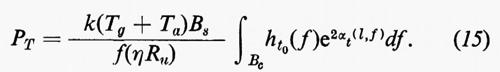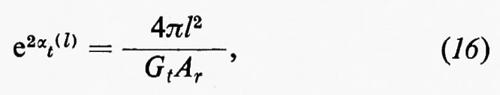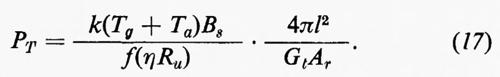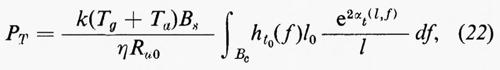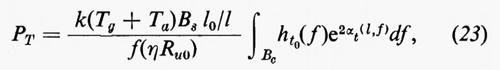Informazione, trattamento e trasmissione della

Informazione, trattamento e trasmissione della

di Francesco Carassa e Emilio Gatti

Informazione, trattamento e trasmissione della

sommario: 1. Introduzione. 2. Quantità di informazione e codificazione. 3. Rappresentazione dei segnali in forma numerica e in forma analogica. 4. Caratteristiche di trasmissione dei sistemi di telecomunicazioni. 5. Trasmissione dei segnali fonici e dei segnali visivi. 6. Propagazione. 7. Disturbi di trasmissione. 8. Amplificazione (con cenni sulle funzioni di trasferimento). 9. La retroazione. 10. Cenni di automatica. 11. Modulazione e demodulazione. 12. Sistemi di trasmissione: a) sistema con una sola tratta; b) sistemi con più tratte; c) reti di comunicazione e commutazione. □ Bibliografia.

1. Introduzione

L'acquisizione, la trasmissione, la conservazione e la presentazione dell'informazione sono elementi essenziali della vita del mondo e sono resi possibili dall'esistenza di appropriati linguaggi stabiliti dalla natura (come per es. quelli per mantenere i caratteri di una specie o quelli per modificare gli stimoli trasmessi dai nostri sensi al cervello) o creati dagli uomini per sviluppare la loro vita di relazione e per accedere a quella grande memoria organizzata che si chiama cultura (v. anche radiotelevisione).

L'elettronica, fornendo i mezzi più idonei al trattamento dell'informazione, ha dato un contributo determinante allo studio del concetto stesso di informazione e alla ricerca di una definizione scientifica della quantità di informazione recata da un messaggio.

2. Quantità di informazione e codificazione

Cominciamo col definire come istruzione elementare (o istruzione binaria) quella che determina la scelta fra due sole alternative possibili che possono essere indicate per esempio con le cifre binarie 0 e 1. La quantità di informazione di un certo messaggio, facente parte di un insieme di messaggi possibili del quale siano note le caratteristiche statistiche, può essere allora data dal minimo numero (statistico medio) di istruzioni elementari da impartire a una opportuna macchina, comunque complicata, affinché essa possa riprodurre, con la qualità desiderata, il messaggio stesso. La macchina ipotizzata potrebbe essere per esempio una ‛macchina parlante' azionata da una sequenza di istruzioni binarie: in questo caso la misura della quantità di informazione I recata da un messaggio fonico sarebbe data dal minimo numero statistico medio di istruzioni binarie necessarie alla macchina per riprodurre il messaggio stesso (la media statistica va intesa come media sull'insieme dei messaggi che si prevede possano essere trasmessi).

In forma matematica la quantità di informazione può essere espressa, nel caso in cui i messaggi possibili siano M, e cioè m₁, m₂, ... m_M, con rispettive probabilità P_m1, P_m2, P_mM, dalla relazione

che, nel caso particolare di equiprobabilità dei messaggi (probabilità di ogni messaggio pari a 1/M), si riduce a

I=log₂M.

Il significato di tale espressione è evidente nel caso in cui M sia una potenza di 2, per es. M=2^N. Si ha infatti I=N ed N è appunto il numero di istruzioni necessarie per isolare il singolo messaggio dall'insieme degli M messaggi possibili, ciò che può essere fatto dimezzando ripetutamente, per N volte, l'insieme dei messaggi e scegliendo via via delle due classi (di M/2, M/2², ... M/2^N=M/M=1 elementi) quella che contiene il messaggio.

La quantità di informazione è stata definita in modo da essere additiva: infatti, accoppiando ciascuno degli M messaggi equiprobabili a ciascun messaggio di un'altra serie di Q messaggi equiprobabili, il complesso di messaggi diversi è MQ e pertanto la quantità di informazione complessiva log₂(MQ) è pari alla somma delle quantità di informazione log₂M+log₂Q portate dalle due classi singolarmente.

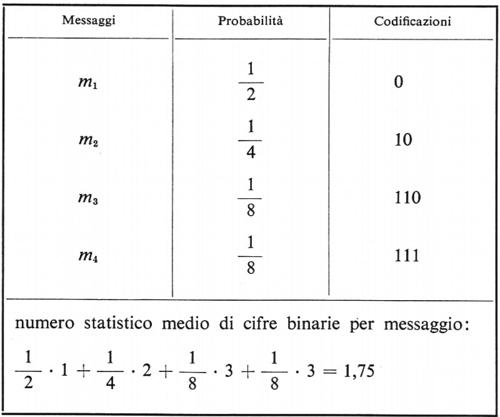
Ritorniamo all'esempio precedente di M=2^N e supponiamo che l'insieme sia formato da quattro messaggi equiprobabili; il numero N di istruzioni binarie occorrenti per individuare ciascun messaggio risulta allora eguale a 2 e i quattro messaggi possono essere completamente individuati, e cioè possono essere ‛codificati', con le seguenti quattro coppie di cifre binarie: 00, 01, 10, 11. Nel caso di messaggi non equiprobabili la quantità di informazione recata da ciascuno di essi è mediamente inferiore a log₂ M, come si può constatare notando che il numero minimo statistico medio di istruzioni binarie necessarie per isolare un messaggio dall'insieme dei messaggi possibili è minore di quello corrispondente al caso di equiprobabilità. Infatti, riprendendo l'esempio di quattro messaggi, ma attribuendo a questi probabilità diverse, come indicato nella tabella, si può mostrare che la codificazione più conveniente è quella in cui i messaggi sono codificati non con un numero costante di cifre binarie, ma seguendo la regola di attribuire le successive cifre a gruppi equiprobabili di messaggi: con la prima cifra si scevera tra il messaggio m₁ di probabilità 1/2 e i restanti messaggi m₂, m₃, m₄ (di probabilità complessiva 1/4 + 1/8 + 1/8=1/2), con la seconda si scevera tra m₂ e il gruppo di due messaggi m₃ e m₄, e infine con la terza fra m₃ e m₄; cosicché i messaggi più probabili risultano codificati da un numero più piccolo di cifre binarie.

Si vede dalla tabella che in questo modo il numero statistico medio di cifre binarie, o bits (da binary digits), per messaggio, si è ridotto dal valore 2 (corrispondente alla codificazione a numero costante di cifre binarie) al valore 1,75. Tale valore anzi, nell'esempio particolare scelto, è uguale alla quantità di informazione ricavabile dalla (1) per il caso in esame e quindi la codificazione scelta è quella ottima, cioè è quella che corrisponde al minimo numero statistico medio di istruzioni binarie per messaggio. (Si noti che la codificazione scelta, pur riducendo al minimo le istruzioni, permette ancora di distinguere fra loro i successivi messaggi di una sequenza; questi infatti terminano tutti con la cifra 0 ad eccezione dell'ultimo caratterizzato da tre 1 consecutivi. Tenendo presente questa regola, risulta definita in modo univoco la segmentazione di una qualsiasi sequenza di cifre binarie; per es., data la sequenza 101101111100 è immediato decidere per la seguente segmentazione: 10/110/111/110/0).

È interessante osservare la connessione del concetto di informazione sopra definito con quello di entropia, quale misura del grado di incertezza della configurazione microscopica di un sistema macroscopico. È ben nota in meccanica statistica la definizione di entropia:

S=klog_eW=−klog_ep,

dove k è la costante di Boltzmann e W è, nel linguaggio di Plank, il numero di complessioni, ovvero di configurazioni microscopiche distinguibili equiprobabili, ciascuna di probabilità p = 1/W. L'introduzione in meccanica statistica della costante k di Boltzmann nella definizione di S e l'impiego del logaritmo naturale è una scelta di convenienza per far coincidere l'entropia così definita con quella definita, in base a ragionamenti termodinamici macroscopici, mediante la

A questo riguardo, e in particolare per la rimozione del paradosso del diavoletto di Maxwell mediante il concetto di informazione, rimandiamo ai lavori di Brillouin.

I messaggi si presentano spesso come sequenze di messaggi elementari: è di rilevante interesse il caso in cui ciascuno dei messaggi elementari sia tratto dallo stesso insieme di messaggi possibili; ciò accade, per esempio, nel linguaggio scritto in cui ogni simbolo o lettera è tolto dallo stesso alfabeto. Riferendoci a questo caso si deve osservare che l'informazione di una sequenza di n simboli è n volte l'informazione di ciascuno di essi, solo se questi sono statisticamente indipendenti, ovvero se l'occorrenza di ciascun simbolo non è condizionata dall'occorrenza di determinati simboli precedenti. Se invece esiste una dipendenza statistica, l'informazione mediamente portata da un simbolo in un messaggio lungo, è minore di quella recata dal simbolo stesso singolarmente. Per la lingua italiana, messe in conto le dipendenze statistiche di una lettera dalle precedenti e, naturalmente, la diversa frequenza (cioè la diversa probabilità) delle lettere stesse, l'informazione recata da ogni lettera si riduce al 40% rispetto a quella che si avrebbe in un linguaggio dove le lettere fossero equiprobabili e statisticamente indipendenti. Per la lingua inglese detto rapporto è del 32%.

Nel caso delle telescriventi sono usati 32 simboli diversi, ciascuno dei quali viene trasmesso con 5 bits, come se i simboli fossero equiprobabili e statisticamente indipendenti; di conseguenza le telescriventi sono in grado di trasmettere non solo le sequenze di un determinato linguaggio, ma qualsiasi sequenza: per esempio, messaggi cifrati. (Quando una telescrivente è usata per una determinata lingua, la codificazione non è quindi ottima, ma si ha una certa ‛ridondanza', cioè l'informazione trasmessa è maggiore di quella necessaria per individuare il simbolo; la ridondanza non è però generalmente inutile perché può servire a correggere automaticamente - mediante l'uso di opportune apparecchiature - gli errori che si verificano durante la trasmissione, oppure può aiutare il ‛ricevitore umano', che conosce grammatica e sintassi della lingua, a correggere molti degli errori, o delle interruzioni, di un segnale recante un messaggio).

3. Rappresentazione dei segnali in forma numerica e in forma analogica

Sinora abbiamo parlato di sorgenti ‛discrete' di messaggi: cioè di sorgenti che emettono messaggi (o sequenze di messaggi) scelti fra un numero finito di messaggi possibili. Rientrano in questa categoria, oltre agli scritti, tutti i segnali che rappresentano numeri, per esempio i segnali destinati alla trasmissione di informazioni tra calcolatori elettronici, al controllo numerico di impianti o all'acquisizione di dati. In particolare può essere citato il caso, sempre possibile, in cui i messaggi vengono rappresentati mediante sequenze di simboli binari; la trasmissione viene allora frequentemente attuata associando ai due stati rappresentativi due forme d'onda eguali e di segno opposto; per esempio il segnale può essere del tipo illustrato nella fig. 1, in cui in ogni intervallo di tempo riservato a un simbolo binario (1 oppure 0) la corrente ha un determinato verso. In realtà molte sorgenti continue (cioè in grado di emettere un numero infinito di messaggi) sono associate a un organo ‛quantizzatore'. Un caso tipico può essere quello in cui il messaggio sia la misura di una grandezza fisica, per esempio di una temperatura. La temperatura può assumere tutti i valori di un certo intervallo e può essere rappresentata elettricamente da una corrente proporzionale a essa, ottenuta mediante un adeguato ‛trasduttore': la grandezza continua in esame è in tal caso rappresentata analogicamente. Se invece della temperatura si prende come messaggio la sua lettura numerica sulla scala graduata di un termometro (limitandosi per es. a due sole cifre significative), il numero dei messaggi possibili diventa finito e la grandezza continua originaria risulta rappresentata numericamente. La rappresentazione numerica comporta necessariamente un ‛errore di quantizzazione' che è tanto più piccolo quanto più grande è il numero di cifre usato; pertanto con un adeguato numero di cifre si può rendere questo errore più piccolo del massimo errore tollerabile dall'utilizzatore. D'altra parte la quantizzazione può far conseguire vantaggi di particolare rilevanza nella tecnica delle telecomunicazioni quando si mettano in conto i disturbi di trasmissione (v. sotto, cap. 7).

4. Caratteristiche di trasmissione dei sistemi di telecomunicazioni

In pratica una sorgente, discreta o continua, emette sequenze di messaggi, che debbono essere inviati sotto forma di segnali elettrici, su un supporto fisico costituito da un insieme di apparecchiature e di mezzi trasmissivi (canale); sorge quindi il problema di sapere: a) in quanto tempo può essere trasmesso un certo messaggio da un certo canale; b) quale insieme di apparecchiature va predisposto per trasmettere un certo messaggio in un certo tempo.

La scelta della durata di trasmissione del messaggio è possibile soltanto quando il messaggio stesso possa essere memorizzato e poi letto dalla memoria con velocità qualsiasi; questa possibilità non è sempre concessa e anzi vi sono importanti casi in cui il messaggio va trasmesso con lo stesso ritmo con cui è generato. In molte applicazioni interessa non solo la durata di trasmissione di un messaggio, ma anche il ritardo con cui esso è reso disponibile all'utente. Questo ritardo è sempre presente anche quando non si predispongano organi di memoria e il messaggio venga trasmesso con lo stesso ritmo con cui è generato: infatti i mezzi di trasmissione a distanza sono caratterizzati da una velocità finita di propagazione, cioè sono inevitabilmente essi stessi organi di memoria temporanea. Si può definire ‛trasmissione in tempo reale' quella che avviene in tempi piccoli a confronto del tempo di elaborazione da parte degli utilizzatori (esseri umani o calcolatori); in altre parole quando i due utilizzatori sono messi in grado di comunicare fra loro senza che la presenza del ritardo condizioni in modo essenziale il colloquio.

È interessante osservare che la propagazione per via elettromagnetica nel vuoto (e in pratica nella maggior parte dei mezzi di trasmissione) avviene con velocità tale che, anche alle massime distanze possibili tra due punti sulla Terra, o in prossimità di questa, il tempo di trasmissione è ancora abbastanza piccolo (dell'ordine del decimo di secondo) per soddisfare la sopra citata condizione per la trasmissione in tempo reale fra esseri umani. Una caratteristica fondamentale che determina la durata minima di trasmissione di un messaggio attraverso un certo canale è la ‛larghezza di banda' di quest'ultimo, ossia l'intervallo di frequenza delle componenti spettrali del segnale che questo riesce a trasmettere dalla sua entrata alla sua uscita.

Consideriamo, come primo riferimento, l'importante caso ideale in cui la caratteristica di trasmissione dell'apparecchiatura sia quella rappresentata nella fig. 2, tale cioè da trasmettere inalterate in ampiezza tutte le componenti con frequenza da 0 a f_c, sfasandole di un angolo ϕ proporzionale ad f (cioè ritardandole di un tempo τ costante per tutte). Se immaginiamo che un determinato segnale (o simbolo) sia rappresentato da un certo impulso (v. fig. 3A), alla cui ampiezza P è affidata l'informazione da trasmettere, osserviamo che al diminuire della durata δ di tale impulso, l'impulso all'uscita dell'apparecchiatura (v. fig. 3B) tende a una forma costante che non dipende dalla forma dell'impulso di eccitazione (salvo che per l'ampiezza Q proporzionale all'area dell'impulso di eccitazione), ma dalla caratteristica di trasmissione dell'apparecchiatura. Come è noto dalla teoria delle trasformate di Fourier, la forma d'onda della fig. 3B, che è la risposta all'impulso da parte di un sistema avente la caratteristica di trasmissione rappresentata nella fig. 3, è caratterizzata dalla presenza di zeri a intervalli di 1/(2f_c) secondi intorno al centro dell'impulso principale. Se ne deduce che, attraverso il sistema con larghezza di banda B=f_c−0=f_c, è possibile trasmettere simboli indipendenti alla velocità di 2f_c simboli al secondo. Infatti, con questa velocità, due generici simboli successivi si presentano all'uscita come nella fig. 4, e l'ampiezza di ciascuno di essi può essere letta in corrispondenza del suo massimo dove tutti gli altri impulsi hanno ampiezza zero.

In generale si può dire che, in un certo intervallo di tempo t, per un sistema di larghezza di banda B, sono disponibili 2Bt parametri indipendenti con cui definire le forme d'onda trasmissibili. Per evitare che piccole variazioni della velocità di trasmissione, ovvero della caratteristica di fig. 2, possano dar luogo a forti interferenze fra i simboli, e in considerazione anche della difficoltà di ottenere caratteristiche di trasmissione abbastanza vicine a quella ideale, si preferiscono in pratica soluzioni sub-ottime, con caratteristiche d'ampiezza di andamento meno brusco (v. fig. 5A), che hanno forme d'onda d'uscita con ondulazioni meno accentuate (v. fig. 5B).

Il teorema del campionamento, derivante dal fatto già citato che, in un tempo t, il segnale uscente da un sistema con banda B è caratterizzato da 2Bt parametri indipendenti, assicura che un segnale di banda finita B è completamente definito dai suoi campioni purché questi si susseguano con frequenza non inferiore a 2B.

La fig. 6 mostra in A un segnale continuo e in B il suo spettro: lo stesso segnale dopo campionamento e il relativo spettro sono mostrati nella fig. 6, C e D.

Il nuovo spettro contiene quello del segnale originale e quindi quest'ultimo può essere sempre ricostruito con un filtro che abbia caratteristica d'ampiezza del tipo visto nella fig. 5 (tale caratteristica è riportata nella fig. 6D) e caratteristica di fase proporzionale alla frequenza nella banda del segnale originario. Si noti che nella fig. 6 si è assunta una frequenza f₀ di campionamento sensibilmente superiore al minimo teorico 2f_c per avere un intervallo di frequenza f_c÷(f₀−f_c), privo di componenti spettrali del segnale, che permetta di usare un filtro reale, con caratteristica d'ampiezza che cada a zero in modo non brusco entro il suddetto intervallo.

Da quanto precede risulta che un segnale con banda limitata può essere trasmesso mediante suoi campioni, presi con frequenza maggiore o, nell'ipotesi di filtro ideale, uguale al doppio della banda del segnale. Tali campioni possono essere trasmessi in forma analogica, cioè come impulsi successivi di diversa ampiezza (per esempio, nel caso più semplice, come impulsi di ampiezza proporzionale all'ampiezza istantanea del segnale), e in questo caso la minima banda di trasmissione è pari alla banda del segnale e la trasmissione dei campioni con banda 0÷f_c equivale alla trasmissione del segnale non campionato; oppure in forma numerica, trasmettendo, nell'intervallo tra un campione e il successivo, la serie di impulsi che rappresenta, ad esempio in codice binario, con un conveniente numero K di cifre, il valore numerico dell'ampiezza del campione stesso (nel caso binario gli impulsi possono avere due sole ampiezze, come in fig. 1) e allargando del fattore K la banda per consentire la trasmissione di questi impulsi con frequenza di ripetizione Kf_c.

5. Trasmissione dei segnali fonici e dei segnali visivi

Si è accennato (v. sopra, cap. 3), parlando dei segnali continui, ai segnali ‛naturali', derivati dalla misura di una grandezza fisica. Nella pratica, i più importanti segnali di questa classe sono i segnali utilizzati nella comunicazione umana diretta e recepiti dai nostri sensi; tra questi segnali, occupa il primo posto per importanza e diffusione il segnale fonico che viene trasformato in segnale elettrico (v. elettronica, capp. 4 e 11) mediante un trasduttore acustico-elettrico (microfono) e successivamente ritrasformato in segnale fonico mediante un trasduttore elettrico-acustico (per esempio un altoparlante). Grande importanza ha anche il segnale visivo per il quale sono utilizzati trasduttori fotoelettrici per tradurre in segnale elettrico la luminanza dei vari punti delle immagini da trasmettere, e trasduttori elettroluminescenti per l'operazione inversa.

La trasmissione dei segnali per la comunicazione umana comporta problemi notevolmente più complessi di quelli che si incontrano nella comunicazione fra automi e in particolare fra calcolatori. In quest'ultimo caso si tratta infatti di segnali originariamente in forma numerica, e praticamente l'unico aspetto che ne caratterizza la ‛qualità' di trasmissione è la possibilità di errori nei simboli ricevuti. Al contrario i segnali per la comunicazione umana diretta implicano aspetti qualitativi, non facilmente definibili perché legati ai giudizi soggettivi dei vari individui: per esempio nel caso del segnale telefonico, la voce riprodotta in ricezione deve essere non soltanto comprensibile, ma anche gradevole e dovrebbe possibilmente conservare quelle sfumature significative che coloriscono il linguaggio parlato consentendo il riconoscimento dell'interlocutore.

A causa della difficoltà di dare a questi requisiti un valore quantitativo, il problema di valutare il contenuto d'informazione del segnale fonico naturale risulta estremamente complesso. Il problema si semplifica se si richiede la sola intelligibilità del discorso: infatti in questo caso il contenuto di informazione è quello stesso del corrispondente linguaggio scritto. Come si è già detto, nella lingua italiana la quantità di informazione recata mediamente da ogni lettera è ridotta al 40% dei 5 bits necessari per individuare una lettera dell'alfabeto presa singolarmente; la quantità di informazione di ogni lettera è quindi di circa 2 bits. Poiché parlando si pronunciano parole corrispondenti a circa 15 lettere al secondo, il ritmo di emissione dell'informazione mediante la voce (ai fini della pura intelligibilità) è intorno ai 30 bit/s. Se invece si vogliono conservare in modo soddisfacente le varie caratteristiche della voce cui s'è prima accennato, occorre tenere presente che il canale per la connessione diretta fra microfono e ricevitore telefonico deve lasciar passare almeno la banda fra 300 e 3.400 Hz; ciò comporta, nel caso di trasmissione campionata, una frequenza di campionamento di 8.000 Hz e, nel caso di trasmissione numerica, un ritmo di 64.000 bit/s, essendosi trovato che, sempre per il soddisfacimento dei requisiti citati, occorrono 8 cifre binarie per campione. Se, dunque, in luogo di quest'ultimo semplice sistema di trasmissione, si disponesse al terminale trasmittente di una macchina automatica cui dettare, e a quello ricevente di una macchina automatica capace di leggere, sarebbe possibile un risparmio di circa 2.000 volte nel ritmo di trasmissione con soppressione quasi totale della ridondanza; tale sistema, che peraltro toglierebbe ogni colorito originario alla conversazione, sarebbe estremamente complicato. Un'accurata indagine delle caratteristiche della voce ha permesso di giungere a soluzioni intermedie rappresentate dalle apparecchiature denominate ‛vocoders' (voice coders), con le quali il ritmo di trasmissione necessario per il segnale fonico può essere ridotto a qualche migliaio di bits al secondo.

Anche il segnale televisivo, ottenuto ‛scandendo' l'immagine per righe, è un segnale fortemente ridondante, perché tutti i circa 400.000 punti che definiscono l'immagine televisiva sono analizzati 25 volte al secondo, come se tra loro non esistesse alcuna correlazione spaziale e temporale. In tale ipotesi la massima frequenza che occorre trasmettere è di 5 MHz e questa è appunto la banda del segnale televisivo adottata in Italia e nei vari paesi d'Europa. Poiché la notevole estensione della banda di frequenza da trasmettere (più di mille volte superiore a quella del segnale telefonico) vincola fortemente la diffusione di questo importante tipo di informazione, è evidente l'interesse di ridurre la larghezza di banda del segnale televisivo a spese della ridondanza di quest'ultimo, certamente notevole perché in realtà grandi aree delle immagini da trasmettere hanno luminanza uniforme e inoltre molte parti di un'immagine restano inalterate passando all'immagine successiva.

6. Propagazione

La trasmissione dei segnali elettrici è ottenuta mediante la propagazione di onde elettromagnetiche. Queste possono essere guidate da linee bifilari o coassiali e, a frequenze più elevate (microonde), da guide d'onda o addirittura (nel campo del visibile) da fibre ottiche; oppure possono essere irradiate mediante un'antenna trasmittente, o radiatore, e lasciate propagare nello spazio fino all'antenna ricevente, o captatore.

Propagazione delle onde guidate. - Nel caso delle onde guidate la potenza viaggiante decresce esponenzialmente con la distanza; pertanto l'attenuazione, cioè il rapporto espresso in unità logaritmiche (neper, decibel) fra le potenze di segnale all'inizio e alla fine di un determinato percorso è proporzionale alla lunghezza del percorso stesso; in più, nei mezzi attualmente usati in pratica (linee bifilari e coassiali, v. fig. 7, A e B) e, in generale, in tutti i sistemi di guida dove si abbiano correnti longitudinali, l'attenuazione è proporzionale alla radice quadrata della frequenza a causa del cosiddetto ‛effetto pelle', cioè della penetrazione, dipendente dalla frequenza, dell'onda nei conduttori di guida. Questo fatto ha portato a ridurre la banda di trasmissione allo stretto necessario. Le linee bifilari vengono usate come ‛linee aeree' montate su apposite palificazioni, oppure come ‛linee in cavo', nel qual caso esse sono contenute, in numero anche elevato, nello stesso cavo. Le linee bifilari hanno il difetto di produrre un campo elettromagnetico che si estende intorno ai due conduttori e causa accoppiamenti con le linee adiacenti; tali accoppiamenti aumentano con la frequenza e rendono raro l'uso di questo mezzo trasmissivo al di sopra di qualche centinaio di chilohertz. A frequenze superiori conviene usare la linea coassiale che è completamente schermata. La guida d'onda a sezione circolare usata nel modo TE₀₁ (v. fig. 7C) offre il grande vantaggio di presentare un'attenuazione che, anziché crescere, decresce con la frequenza; ciò è dovuto al fatto che nel modo TE₀₁ si hanno soltanto correnti trasversali che decrescono con la frequenza. Nella pratica, la non perfetta levigatezza delle pareti della guida fa sì che l'attenuazione, al di là di certe frequenze, ricominci a crescere; comunque guide sperimentali a sezione circolare, con diametro di 5 cm, hanno mostrato la possibilità di trasmettere, con attenuazione dell'ordine di 1÷2 dB/km, l'enorme intervallo di frequenze fra 30 e 100 GHz. Queste guide d'onda appaiono già oggi competitive rispetto alle linee coassiali sui percorsi di grande traffico. Circa le fibre ottiche è ancora prematuro fare previsioni, per quanto esse sembrino poter presentare caratteristiche molto interessanti: nel settembre 1974 sono state ottenute attenuazioni di soli 1÷2 dB/km su lunghezze di alcune centinaia di metri.

Propagazione delle onde irradiate

Quando, invece di onde guidate, si usano onde irradiate, l'attenuazione cresce con la distanza in modo assai diversificato. Nel caso in cui la propagazione avvenga nel vuoto, la potenza decresce con il quadrato della distanza e cioè molto più lentamente che nel caso delle onde guidate. Questo si verifica praticamente anche nell'aria omogenea (e cioè ben rimescolata) fino a frequenze di circa 10 GHz, che ancora non subiscono assorbimenti da parte dei gas dell'atmosfera e delle precipitazioni; occorre però che non si sentano gli effetti degli ostacoli, che sono rappresentati soprattutto dalla Terra con le sue varie caratteristiche (montagne, laghi, monti, costruzioni, vegetazioni, ecc.).

La trasmissione senza ostacoli si attua in pratica nei collegamenti fra Terra e spazio e cioè nei collegamenti con altri corpi celesti, con satelliti artificiali, o con veicoli per l'esplorazione spaziale. In questi casi, usando antenne direttive puntate verso lo spazio (v. fig. 8), l'effetto dei corpi su cui l'antenna è appoggiata può essere reso trascurabile. Va però ricordato che la Terra è circondata da una zona ionizzata (ionosfera) provocata dall'azione delle radiazioni ultraviolette emesse dal Sole sulle molecole dell'atmosfera; questa zona impedisce alle onde elettromagnetiche di frequenza più bassa di uscire dall'ambito terrestre. Un tipico andamento della densità elettronica N con l'altezza è riportato nella fig. 9: in essa si nota la presenza di più di un massimo (per cui si parla di ‛strati' ionizzati).

La densità elettronica varia molto nel tempo e dipende dall'ora del giorno, dalla stagione e dal ciclo delle macchie solari. Le particelle cariche (elettroni e ioni positivi) presenti nella ionosfera vengono messe in moto dalle forze esercitate su di esse dal campo elettromagnetico dell'onda in transito; di conseguenza, si produce sia una certa dissipazione di potenza dell'onda, sia una diminuzione della costante dielettrica e quindi dell'indice di rifrazione del mezzo. Questa diminuzione è tanto più sensibile quanto maggiore è la densità elettronica (variabile col tempo e con l'altezza) e quanto più bassa è la frequenza dell'onda elettromagnetica. Entrando nella ionosfera, le onde elettromagnetiche, di determinata frequenza f, incontrano quindi un indice di rifrazione n, variabile con l'altezza, e il loro percorso (‛raggio') si incurva; se ψ₀ è l'angolo di incidenza del raggio con la ionosfera, l'angolo ψ in un punto qualunque della traiettoria nella ionosfera è legato all'indice di rifrazione n e a ψ₀ dalla relazione:

n cos ψ=cos ψ₀.

Poiché entrando nella ionosfera n va decrescendo, anche ψ diminuisce e, se si raggiunge un punto in cui ψ=0, il raggio viene rimandato verso la Terra (raggio indicato con linea continua nella fig. 10). Affinché questo accada, occorre che sia

n=cos ψ₀. (2)

Dato che, a parità di densità elettronica, l'indice di rifrazione diminuisce all'abbassarsi della frequenza, quanto più grande è l'angolo di incidenza, tanto più bassa è la frequenza per cui la (2) viene soddisfatta; per frequenze così basse da annullare n, si ha riflessione verso Terra anche per incidenza normale (ψ₀=π2). Per frequenze supenori l'indice di rifrazione non si annulla più e la riflessione ha luogo solo per angoli d'incidenza ψ₀ abbastanza piccoli, mentre per angoli più grandi le onde elettromagnetiche non si riflettono, ma seguono un percorso del tipo di quello indicato dalla linea a tratti della fig. 10. D'altra parte esiste un angolo di incidenza minimo dovuto al fatto che una emissione non può provenire dalla Terra con angolo di incidenza minore di quello corrispondente a radiazione radente (percorso a tratti e punti della fig. 10). Le onde elettromagnetiche di frequenza superiore a circa 30 MHz attraversano in ogni caso la ionosfera e possono quindi essere usate nei radiocollegamenti spaziali. Al di sopra dei 10 GHz si cominciano a verificare le già citate attenuazioni dovute ai gas e alle gocce d'acqua contenute nell'atmosfera; l'effetto maggiore è quello della pioggia, che come si vede nella fig. 11, cresce al crescere della frequenza e dell'intensità della pioggia. Gli scrosci violenti hanno fortunatamente estensione limitata, così che nei collegamenti fra Terra e spazio e viceversa si può operare per ‛diversità di posizione' installando, in luogo di una sola, due postazioni terrestri distanti fra loro una decina di chilometri, per poter scegliere di volta in volta la posizione più favorevole.

Per i radio-collegamenti fra punti a terra, la conformazione della Terra e la presenza della ionosfera giocano un ruolo fondamentale. Per frequenze inferiori a 30 MHz si possono realizzare collegamenti mediante propagazione lungo la superficie terrestre, anche superandone la curvatura, ma solo la riflessione ionosferica può consentire collegamenti fino alle massime distanze intercontinentali.

Quando le onde elettromagnetiche giungono al ricevitore secondo entrambi i percorsi ionosferico e superficiale, oppure attraverso la sola riflessione ionosferica, ma con percorsi multipli, possono insorgere fenomeni interferenziali che provocano variazioni dell'intensità del segnale in funzione sia del tempo, sia della frequenza; perché le variazioni con la frequenza siano piccole entro la banda occupata dal segnale, è necessario che le componenti che interferiscono abbiano fase relativa poco variabile con la frequenza: ciò si verifica se la banda del segnale è piccola rispetto all'inverso delle differenze di ritardo. Poiché per radio-collegamenti per riflessione ionosferica tali differenze possono essere dell'ordine del millisecondo, la banda di trasmissione non può superare in questo caso qualche migliaio di hertz.

Le onde di frequenza inferiore a 30 MHz non sono idonee alla trasmissione di grandi quantità d'informazione, perché l'intervallo di frequenze disponibili è modesto, la distorsione spettrale è notevole per segnali a banda larga e il pericolo di interferenze limita l'uso delle medesime frequenze per attuare più collegamenti simultanei in una stessa zona. I collegamenti radio per la trasmissione di grandi quantità di informazione, ivi incluso il segnale televisivo, si devono pertanto sviluppare a frequenze superiori a 30 MHz. Queste si propagano bene soltanto entro l'orizzonte ottico del trasmettitore, mentre, oltre l'orizzonte, la propagazione può ancora avvenire per diffrazione o per diffusione (diffusione ionosferica fra 30 e 60 MHz, diffusione troposferica a frequenze superiori), ma con attenuazione rapidamente crescente con la frequenza e con la distanza. I collegamenti a grande distanza sono pertanto attuati in generale mediante successive rice-trasmissioni tra postazioni in visibilità (o quasi) una dell'altra. Anche per questi collegamenti si possono verificare percorsi multipli: alle frequenze inferiori al gigahertz essi sono dovuti a interferenze fra raggio diretto e raggio riflesso sul suolo; alle frequenze più elevate la riflessione sul suolo diventa meno importante (salvo che su specchi d'acqua), perché la rugosità del terreno diventa confrontabile con la lunghezza d'onda, e la possibilità di percorsi multipli è determinata dalle irregolarità dell'indice di rifrazione nella troposfera. Rispetto al caso della propagazione ionosferica, le differenze di ritardo sono molto più piccole a causa della brevità del percorso e le distorsioni spettrali diventano apprezzabili solo se si opera con bande di trasmissione di decine di megahertz e con distanze superiori al centinaio di chilometri.

In generale la distribuzione statistica dell'intensità di segnale nel caso di più contributi, tutti di intensità fra loro confrontabile e con fasi casuali e indipendenti, è la distribuzione di Rayleigh (v. fig. 12); essa si riscontra in pratica nella propagazione per percorsi multipli nella ionosfera e anche in quella a microonde, su percorsi in visibilità, come caso limite al crescere della frequenza e della distanza.

7. Disturbi di trasmissione

Il progetto di qualsiasi sistema di trasmissione deve tendere a fornire all'estremo ricevente un segnale di qualità accettabile, deve cioè ridurre a un'entità sufficientemente piccola gli effetti dei disturbi di trasmissione.

Oltre al disturbo di origine termica, inevitabile in natura, sono presenti in pratica molti altri disturbi. Di questi alcuni sono additivi e indipendenti dal segnale trasmesso: sono cioè disturbi che il sistema di trasmissione sovrappone al segnale. La fig. 13 illustra, a titolo d'esempio, i disturbi captati, a frequenze superiori a 100 MHz, da un'antenna puntata con diversi angoli di elevazione; si nota il caso dei collegamenti terrestri (ϕ≃0⁰) e quello di un'antenna puntata allo zenit (ϕ=90⁰). Altri disturbi sono strettamente dipendenti dal segnale trasmesso: si tratta soprattutto di distorsioni del segnale che possono essere ‛armoniche', cioè provocate dalla presenza di dispositivi non lineari, o ‛spettrali', cioè provocate dal fatto che le caratteristiche di ampiezza e di fase del sistema di trasmissione non sono quelle ideali, indicate nella fig. 2. Altri disturbi, infine, sono dovuti a interferenze da parte dei segnali trasmessi da altri sistemi.

Come si è già accennato, il problema fondamentale della trasmissione è quello di trasmettere il segnale con sufficiente fedeltà in presenza dei disturbi di cui si è parlato. Shannon ha mostrato che su un canale disturbato è teoricamente possibile trovare un metodo di trasmissione (codificazione) tale da assicurare una fedeltà assoluta (probabilità d'errore nulla) finché il ritmo di trasmissione dell'informazione, in bits al secondo, non superi un certo valore massimo C₀ detto capacità limite del canale.

Immaginiamo, per semplicità, di avere un canale con disturbo additivo capace di assumere soltanto due possibili valori ±a e consideriamo un segnale campione, o simbolo, di ampiezza A positiva o negativa. È evidente che se si divide l'ampiezza totale 2 A in gradini di ampiezza appena maggiore di 2 a si hanno A/a gradini e si possono trasmettere n=1+A/a ampiezze diverse senza che il disturbo possa produrre errori (v. fig. 14). Pertanto la quantità d'informazione trasmissibile per simbolo è log₂ (1+A/a) e la quantità d'informazione massima trasmissibile senza errori in una banda di frequenza B nell'unità di tempo è

L'ultima espressione si è ottenuta introducendo l'energia media statistica corrispondente alle ampiezze +a, −a, +3a, −3a, ..., −(n−1)a, supposte equiprobabili. Si ha infatti:

da cui

Nel caso, più comune nella pratica, di rumore additivo gaussiano (che è tra l'altro la situazione limite che si incontra quando, eliminate tutte le altre possibili cause di disturbo, si abbia a che fare col solo rumore termico), il rumore raggiunge, sia pure con probabilità fortemente decrescente, valori comunque alti, ed è evidente che, per quanto grande si faccia l'ampiezza dei gradini considerati nella fig. 14, non si potrebbe mai riuscire a operare con errore sempre nullo, come nel caso precedente. Shannon ha però mostrato che l'operazione con probabilità d'errore nulla è ancora raggiungibile con una codificazione più complessa di quella sopra considerata. Se, invece di prendere un singolo simbolo, come nel caso precedente, si considera un intero insieme di simboli (2Bt simboli tra loro indipendenti in un intervallo di tempo t), si può immaginare che il segnale complessivo, costituito dai 2Bt simboli, sia rappresentato da un punto in uno spazio n-dimensionale con n=2Bt anziché in uno spazio monodimensionale come nel caso della fig. 14. Supponiamo che siano A₁, A₂, ..., A_n le ampiezze degli n simboli costituenti il segnale e che l'energia media statistica di ciascun simbolo sia -A-_i² = E_d = costante. La distanza dall'origine del punto rappresentativo del segnale nello spazio n-dimensionale è

r_s=√-A-₁-²-+-A-₂-²-+-•-•-•-+-A-_n-² ,

che, per n molto grande, diventa

r_s=√-E-_d-=-√-E,

se si indica con E l'energia del segnale. I punti rappresentativi dei segnali stanno quindi sulla superficie di un'ipersfera con raggio pari alla radice dell'energia del segnale (costante per tutti i possibili segnali). Indichiamo con a₁, a₂, ..., a_n, le ampiezze del rumore in corrispondenza degli n simboli, e l'energia media statistica di ciascun campione di rumore sia --a-_i²=E_nd=costante. La distanza dall'origine del punto rappresentativo del solo rumore nello spazio n-dimensionale è

r_n=√-a-₁-²-+-a-₂-²-+-•-•-•-+-a-_n-²- -=√-n-E-_nd=√-E-_n,

dove con E_n si è indicata l'energia totale del rumore. La formula indica che i punti rappresentativi del solo rumore stanno su un'ipersfera con raggio pari alla radice dell'energia di rumore (costante per tutti i campioni di rumore considerati). Quando si riceve segnale misto a rumore, l'energia è E +E_n e il punto rappresentativo è contenuto in un'iperfersfera di raggio √-E-+-E-_n. Se tutti i punti che stanno in un ipersfera di rumore di raggio √-E-_n, centrata intorno al punto S rappresentativo del segnale, sono interpretati come segnale S e non vengono assegnati a nessun altro segnale, il segnale sarà sempre interpretato correttamente nonostante il rumore additivo. Naturalmente il numero totale di segnali distinguibili non può essere maggiore del rapporto fra il volume della ipersfera di raggi √-E-+-E-_n e quello dell'ipersfera di raggio √-E-_n. Cioè, ricordando che il numero di simboli n è pari a 2Bt, il numero massimo di segnali trasmissibili in un tempo t su un canale di banda B non può essere maggiore di:

e quindi la quantità d'informazione trasmissibile al secondo (ritmo di trasmissione) non può superare il valore limite:

Sostituendo al rapporto fra le energie quello fra le potenze si può scrivere:

in cui P_s è la potenza media di segnale e h è la densità spettrale di potenza del rumore. La formula (3) è stata ricavata come valore non superabile del ritmo di trasmissione con errore sempre nullo; si può mostrare, grazie ad alcune considerazioni sulle proprietà delle ipersfere, che il valore C₀ è effettivamente raggiungibile. Finché il ritmo di trasmissione è minore di C₀, è sempre possibile, sul canale di banda B, con potenza ricevuta di segnale P_s e densità spettrale di potenza del rumore h, trovare un codice opportuno, tale da far avvenire la trasmissione con probabilità d'errore arbitrariamente piccola (codificazione ottima); quando il ritmo di trasmissione supera C₀ la trasmissione senza errori è impossibile e anzi la probabilità d'errore diviene molto grande.

Come si vede dalla (3), allargando la banda si può, a pari C₀, ridurre la potenza del segnale che diventa minima per B tendente a infinito; al limite si ha:

P_smin=C₀hlog_e2. (4)

Ne consegue che l'energia minima necessaria per trasmettere un bit vale

E_bmin=hlog_e2

ossia, ricordando che per il rumore termico è h=kT (v. eletttronica, cap. 5, È e):

E_bmin=kTlog_e2. (5)

Le operazioni pratiche di codificazione, miranti a rendere il segnale meno vulnerabile ai disturbi, secondo le indicazioni di Shannon, consistono sostanzialmente nell'introdurre ridondanza artificiale nei segnali trasmessi, così da renderli più distinguibili anche in presenza di rumore (si veda la fine del cap. 2). In tal modo, a parità di qualità del segnale reso all'utente e a parità di rumore all'ingresso del ricevitore, è possibile comunicare con una potenza di segnale più piccola. Tuttavia la capacità di canale C₀ è un limite praticamente irraggiungibile e per avvicinarsi ad essa occorre, nel caso di rumore additivo gaussiano, codificare blocchi molto lunghi di simboli, ossia mettere in gioco memorie di grande capacità. La conoscenza del limite teorico permette tuttavia di impostare correttamente lo studio dei sistemi pratici e di valutarne l'efficienza. Oggi sono già disponibili metodi di codificazione che spesso permettono di contenere gli scostamenti della capacità di canale dalla capacità limite C₀ entro valori dello stesso ordine delle tolleranze di progetto.

Si noti che nel cap. 5 abbiamo esaminato la possibilità di ridurre la ridondanza propria dei segnali, riducendo conseguentemente il ritmo di trasmissione richiesto (e dunque la banda del canale), mentre in questo capitolo consideriamo la possibilità di incrementare artificialmente la ridondanza (aumentando la banda necessaria) per ottenere una minore vulnerabilità al rumore. Le due operazioni possono coesistere (v. fig. 15), poiché la ridondanza aggiunta dalla codificazione è generalmente assai più efficiente di quella propria del segnale nei riguardi del rumore sul particolare canale considerato.

8. Amplificazione (con cenni sulle funzioni di trasferimento)

Una delle operazioni base nel trattamento dell'informazione è la cosiddetta ‛amplificazione', che riproduce alcune delle caratteristiche essenziali di un dato segnale e che contemporaneamente conferisce al segnale d'uscita una potenza maggiore di quella d'ingresso (v. elettronica, fig. 3). I principi fondamentali e i dispositivi su cui sono basati gli amplificatori sono trattati nell'articolo elettronica; nel presente articolo se ne esamineranno le caratteristiche ‛esterne' interessanti ai fini del trattamento e della trasmissione dell'informazione.

Nella maggior parte delle applicazioni si richiede che il segnale d'uscita sia, per quanto possibile, simile a quello d'ingresso, cioè che i due segnali siano legati fra loro da una semplice relazione di proporzionalità; vi sono però anche casi in cui si desidera che il segnale d'uscita sia legato a quello d'ingresso tramite anche altri operatori lineari, come integratori o derivatori. Infine la relazione desiderata fra segnale d'uscita e segnale d'ingresso può anche essere non lineare, per es. logaritmica, quadratica, ecc. Nella pratica si ricorre all'amplificazione tutte le volte che si vuole portare un segnale (che si suppone di piccola potenza, come, per esempio, un segnale ricevuto da un trasmettitore lontano, oppure un segnale prelevato da un sistema fisico in modo da produrre su di esso la minima perturbazione possibile) a un livello di potenza sufficiente per comandare in modo adeguato un determinato organo d'uscita o per consentire ulteriori trattamenti del segnale stesso, senza che il suo contenuto d'informazione subisca sostanziali degradazioni per effetto dei disturbi.

L'amplificatore può essere rappresentato mediante il blocco A di fig. 16 dove si è messa in evidenza, oltre che il segnale d'ingresso e quello d'uscita, rappresentati, per esempio, da due tensioni variabili nel tempo v₁(t) e v₂(t), anche la potenza P che deve essere immessa nell'amplificatore da una sorgente esterna d'energia per associare al segnale d'uscita v₂(t) una potenza maggiore di quella associata al segnale d'ingresso v₁(t). Normalmente l'indicazione relativa a P viene omessa, sottintendendola. La classe più importante di amplificatori è quella degli amplificatori lineari che rientrano a loro volta nella classe dei doppi bipoli lineari. Per questi la variabile d'uscita v₂(t) si ottiene da quella d'ingresso v₁(t) mediante un operatore lineare. Secondo quanto espresso dalla fig. 17 questo operatore effettua la convoluzione del segnale v₁(t) a cui è applicato, con una funzione h(t), detta ‛risposta caratteristica'. Quest'ultima può essere interpretata fisicamente come l'uscita dell'amplificatore quando questo sia eccitato ‛a percossa' da un segnale v₁(t) (v. fig. 18) che, per Δτ→0, si riduca alla funzione impulsiva δ(t) di Dirac, per la quale valgono, come è noto, le relazioni:

Con tali ipotesi per v₁(t), l'integrale di convoluzione di fig. 17 fornisce per v₂(t), la funzione h(t) stessa. In generale l'espressione di fig. 17 indica che il segnale d'uscita v₂(t) può essere costruito, data la supposta linearità del sistema, mediante la somma delle risposte v₁(t)dt•h(t−τ) a percosse elementari v₁(τ)dτ, date al sistema dal segnale d'ingresso v₁(τ), dall'istante zero (prima del quale si hanno v₁(τ)dτ identicamente nulle) sino al tempo τ=t a cui si osserva l'uscita.

Alla relazione causa-effetto espressa nella fig. 17 si può dare una rappresentazione più semplice, molto utilizzata in elettronica, facendo corrispondere, per il noto teorema di Borel, al prodotto integrale il semplice prodotto delle corrispondenti trasformate di Laplace; si ha così:

V₂(p)=H(p)V₁(p),

dove le tre grandezze V₂, V₁ e H sono funzioni della variabile complessa p=α+jω. Di H(p), detta ‛funzione di trasferimento' del sistema considerato, si può dare una rappresentazione intuitiva nel caso di segnali sinusoidali smorzati o esaltati, rappresentabili in forma complessa (dando significato fisico alla sola parte reale) mediante funzioni del tipo V(α+jω) e^(α+jω)t con α e ω costanti. In questo caso la funzione H(α+jω) specifica, col suo modulo e la sua fase, l'attenuazione e lo sfasamento del segnale d'uscita V(α+jω) e^(α+jω)t (effetto) rispetto al segnale d'ingresso V₁(α+jω) e^(α+jω)t (causa). Il fatto che i sistemi lineari eccitati con funzioni del tipo K e^(α+jω)t rispondano (a meno di transitori) con funzioni caratterizzate dallo stesso esponenziale e^αt e dalla stessa pulsazione ω e che, eccitati a percossa, vibrino liberamente con forme d'onda del tipo ΣA_i e^pit, è di fondamentale importanza: ad esso corrisponde il fatto che i sistemi lineari si possono rappresentare mediante equazioni differenziali lineari.

Si osserva infine che le forme d'onda sinusoidali di continuo uso in elettrotecnica sono un caso particolare di queste funzioni sinusoidali modulate, ottenuto ponendo la costante reale α eguale a zero e considerando le sole pulsazioni ω.

Lo studio delle funzioni di trasferimento e la caratterizzazione dei sistemi per loro tramite è uno dei capitoli più importanti e fecondi dell'elettronica. Non possiamo addentrarci in questo argomento, ma ci limiteremo a dire con Guillemin che le funzioni di trasferimento H(p) e le corrispondenti risposte impulsive h(t), a partire dalle quali sono state introdotte, costituiscono il ‛bread and butter' dell'ingegnere elettronico e il linguaggio base di conversazione in questo campo della tecnica.

Ritorniamo ora all'amplificatore per darne una rappresentazione più completa che metta in evidenza le variabili coniugate alle tensioni v₁(t) e v₂(t) e cioè le correnti i₁(t) e i₂(t) (assorbite ed erogate dall'amplificatore), indispensabili per considerazioni energetiche (v. fig. 19): al segnale d'ingresso è infatti associata la potenza v₁(t)i₁(t) e a quello d'uscita la potenza v₂(t)i₂(t). (Per le tensioni v e le correnti i si deve specificare un senso, scelto arbitrariamente, in cui esse sono da considerare come positive; tale senso viene usualmente indicato da frecce. Nel caso della fig. 19 sono considerate come positive le tensioni applicate alle due coppie di morsetti di ingresso e d'uscita quando il potenziale del morsetto 1 è superiore a quello del morsetto 1′ e analogamente per i morsetti 2 e 2′; sono da considerare positive le correnti che entrano nel morsetto 1 e quelle che escono dal morsetto 2). Prendendo ancora in esame il caso dell'amplificatore lineare, le variabili d'uscita possono essere espresse mediante quelle d'ingresso tramite operatori lineari A, ℬ, C, D, analoghi all'operatore precedentemente considerato (v. fig. 17). Passando anche in questo caso alle corrispondenti trasformate di Laplace, si ottengono, nel dominio delle frequenze complesse, p, le relazioni:

V₂(p)=A(p)V₁(p)+B(p)I₁(p)

I₂(p)=C(p)V₁(p)+D(p)I₁(p) (6)

che legano le due variabili del segnale d'uscita a quelle del segnale d'entrata e che sono le relazioni più generali di un doppio bipolo lineare. Naturalmente le variabili dipendenti possono essere scelte in vario modo tra le quattro variabili V₁, V₂, I₁, I₂, secondo il particolare problema da affrontare.

Nello studio dei circuiti elettronici, considerati lineari per piccole variazioni dei segnali applicati all'ingresso, sono molto usate le relazioni equivalenti alle (6), esplicitate nei tre modi mostrati nella fig. 20, dove sono messe in luce diverse grandezze caratteristiche dell'amplificatore (o più in generale del doppio bipolo). (Come si vede dallo schema rappresentato nella figura stessa, dette grandezze sono state definite considerando come positive le correnti entranti nei morsetti 1 e 2 del doppio bipolo. Si noti che questa convenzione relativa al senso positivo scelto per la corrente i₂ è l'opposta di quella precedentemente scelta nella fig. 19). Naturalmente tutte le grandezze riportate nelle relazioni della fig. 20 vanno considerate funzioni della variabile complessa p=α+jw. Nelle tabelle a fianco delle relazioni sono definite le relative funzioni di trasferimento. In pratica non è sufficiente specificare i quattro parametri che definiscono un amplificatore lineare secondo una delle tabelle della fig. 20, ma occorre anche indicare la cosiddetta ‛dinamica', cioè le ampiezze massime delle variabili in gioco (tensioni e correnti) perché l'amplificatore possa essere considerato lineare, o alternativamente l'ammontare delle ‛distorsioni' per una determinata ampiezza delle variabili. In secondo luogo occorre specificare quanto ‛rumore' l'amplificatore sovrapponga al segnale. Questo rumore ha diverse origini fisiche: rumore termico (prodotto da elementi dissipativi a temperatura maggiore dello zero assoluto), rumore granulare dovuto alla natura della corrente portata da elettroni con carica quantizzata, ecc. (Questi argomenti sono trattati nel cap. 5 di elettronica, dove viene introdotta la temperatura di rumore che è il parametro adatto a caratterizzare un amplificatore sotto questo aspetto).

Condizione perché un doppio bipolo possa funzionare da amplificatore, o più in generale sia un doppio bipolo attivo, è che esistano delle pulsazioni p=α+jw non smorzate (a≥0) per le quali la potenza uscente complessivamente sia positiva; sia cioè, nella simbologia delle (6):

Re(V₂I₂*−V₁I₁*)> 0; (7)

dove Re sta per ‛parte reale di...' e le grandezze complesse coniugate sono indicate con asterisco.

Affinché la condizione (7) sia soddisfatta, è necessario che sia almeno soddisfatta una delle tre seguenti condizioni fra i coefficienti A, B, C, D:

Re(AC*) > 0 (7.1)

Re(BD*) > 0 (7.2)

Le condizioni (7.1) e (7.2) esprimono il fatto che i morsetti di uscita sono in grado di erogare potenza rispettivamente con i morsetti d'ingresso aperti o in cortocircuito; la (7.3) esprime il fatto che un opportuno circuito passivo, che accoppi i morsetti di uscita con quelli di ingresso, mettendo in atto quella che si usa chiamare una ‛reazione positiva', può consentire l'erogazione di energia da parte del doppio bipolo a determinate pulsazioni (dipendenti dal circuito passivo e dal doppio bipolo attivo considerato), anche con segnale d'ingresso nullo. È su questo principio che funzionano generalmente gli oscillatori.

Conviene, a questo proposito, ricordare che gli oscillatori, adatti a generare segnali periodici (normalmente ad alta frequenza), sono l'organo fondamentale dei trasmettitori e forniscono i segnali sinusoidali usati per le operazioni di modulazione e demodulazione di cui si parlerà nel cap. 11.

Come già detto, le funzioni di trasferimento, che abbiamo introdotto parlando degli amplificatori, sono d'impiego generale in tutti i sistemi lineari; esse in particolare sono alla base dello studio delle reti elettriche, schematizzabili mediante combinazioni di parametri attivi (come quelli che compaiono negli amplificatori sopra considerati) e passivi (come le resistenze, le induttanze e le capacità). Nella fig. 21 sono riportati i simboli convenzionali di questi elementi passivi e le relazioni operazionali tra le tensioni e le correnti ai loro morsetti. La schematizzazione di elementi fisici con elementi concentrati ideali di questo tipo è possibile sino a quando le dimensioni dell'elemento fisico sono molto piccole rispetto alle lunghezze d'onda associate ai segnali da trattare.

Nella fig. 22 è riportata, a titolo d'esempio, una rete passiva costituita con detti elementi; si tratta di un cosiddetto ‛filtro passa basso', ottenuto con due induttanze e due capacità e caratterizzato dalle sue funzioni di trasferimento y₁₁, y₂₂ , y₁₂, y₂₁, calcolate applicando i principi di Kirchhoff e le relazioni fra tensioni e correnti indicate nella fig. 21 per i vari elementi che compongono la rete.

9. La retroazione

Abbiamo occasionalmente accennato (v. sopra, cap. 8) al concetto di reazione positiva, per mostrare come si possa, mediante un amplificatore, generare oscillazioni elettriche, o come in un intero sistema l'informazione possa, con un canale di ritorno, essere portata a influire nuovamente sulla sorgente. La considerazione degli effetti della presenza di anelli chiusi di circolazione di segnali, cioè di ‛retroazione', è così importante e così feconda di risultati (non solo per quanto riguarda gli oscillatori) che è opportuno, anche in questa stringata sintesi, cercare di svilupparla ulteriormente (v. fig. 23).

Consideriamo un amplificatore, caratterizzato per semplicità da una sola funzione di trasferimento A che leghi la tensione d'uscita a quella d'entrata, e supponiamo che il suo ingresso sia alimentato da una differenza di due segna- li: uno esterno e, di comando, e uno βu ricavato dal segna- le d'uscita u tramite una opportuna funzione di trasferimento β. All'ingresso dell'amplificatore sarà presente il segnale e−Βu e potremo scrivere che il segnale d'uscita vale

u=A(e−βu),

da cui

La funzione di trasferimento dell'amplificatore si è cioè modificata a causa della reazione ed è passata da A a

Per il campo di pulsazioni per cui βA≫1, la funzione di trasferimento approssima 1/β e pertanto risulta praticamente indipendente da quella A dell'amplificatore. Se β, come spesso avviene, è determinata da un circuito elettrico passivo di grande stabilità, vengono così a essere minimizzate sia le variazioni nel tempo delle caratteristiche dell'amplificatore, sia le distorsioni da esso introdotte (che possono essere pensate come prodotte da una variazione di A con l'ampiezza del segnale). L'intuizione rende immediatamente conto di queste proprietà della reazione: ogni scarto di βu dal segnale di comando e provoca un segnale di errore (e+βu) che, amplificato per A, porta u al corretto valore che minimizza lo scarto stesso; tale scarto, al limite, diventa nullo se l'amplificatore ha guadagnato A infinito, cioè se è capace di produrre un segnale di uscita u finito con un ingresso (e−βu) infinitesimo. Per semplicità consideriamo la più semplice reazione consistente nel riportare l'uscita all'ingresso (β=1):

L'amplificatore diventa cioè un fedele copiatore con tensione d'uscita u uguale alla tensione di ingresso e. La potenza associata al segnale di uscita u può però essere molto maggiore di quella associata a e: così, per esempio mediante un segnale di tensione con associate potenze di microwatt possiamo comandare, con rigorosa proporzionalità, la velocità di rotazione di un asse di un rullo di laminatoio con associate potenze di centinaia di chilowatt. Ma in generale un amplificatore, che si reaziona nell'intento di conseguire una funzione di trasferimento pari a circa 1/β nella banda passante, resta un amplificatore o diventa un oscillatore? Per poter rispondere a questa domanda bisogna osservare l'uscita quando il segnale di ingresso tende a zero, cioè il limite del rapporto u/e per e tendente a zero. Risulta:

Quando tale limite va a infinito significa che possono esistere segnali di uscita senza che alcun segnale sia applicato all'ingresso e i valori di p per cui ciò si verifica (le p_i=α_i+jω_i sono le radici dell'equazione 1+β(p)A(p)=0) specificano la natura ditali segnali di uscita: essi possono essere dei transitori che si estinguono nel tempo (tutti gli α_i minori di zero) o dei segnali che crescono col tempo (qualche α_i maggiore di zero). Nel primo caso si tratterà di un sistema stabile (cioè di un amplificatore con guadagno prossimo a 1/β per il campo di frequenze di lavoro per cui ∣βA∣≫1); nel secondo di un circuito instabile che può essere un oscillatore o un circuito a scatto. Occorrono particolari cautele nello studio dell'andamento della funzione β(p), se si vuole costruire un amplificatore per cui ∣β(p)A(p)∣ sia molto maggiore di 1 in una larga banda e per cui non si manifestino indesiderate oscillazioni (tutti gli α_i>0). Nel caso invece in cui si consideri un oscillatore o un circuito a scatto, i transitori propri del circuito, corrispondenti a radici con parte reale positiva, determineranno un transitorio crescente che, dopo un certo tempo, sarà stabilizzato per effetto della non linearità del sistema oppure porterà quest'ultimo a distruzione. Il fatto che questo transitorio sia oscillante o aperiodico dipenderà dal rapporto tra il valore della parte immaginaria jω_i delle radici p_i e quello della corrispondente parte reale α_i.

Un oscillatore quasi sinusoidale si avrà quando l'equazione [1+β(p)A(p)]=0 ha, come uniche radici con parte reale positiva, una sola coppia di radici complesse coniugate con ∣±jω_i∣≫α_i. Le non linearità, sempre presenti nei sistemi fisici quando le oscillazioni superano una certa ampiezza, fanno sì che la forma d'onda generata sia, a regime, quasi sinusoidale, mentre all'inizio del funzionamento (inserzione dell'oscillatore) essa ha il caratteristico andamento sinusoidale crescente proprio della pulsazione p_i=α_i+jω_i, con α_i>0 (v. fig. 24).

10. Cenni di automatica

Lo studio dei sistemi con retroazione, cui abbiamo appena accennato per il caso di sistemi lineari, diviene assai complesso passando ai sistemi non lineari, o a sistemi in cui si desiderano controllare contemporaneamente più variabili, o infine a sistemi in cui si debba tener conto della variabilità dei parametri del sistema da controllare.

Il ramo dell'elettronica che si è sviluppato a partire dai concetti di retroazione è detto ‛automatica' e le sue applicazioni vanno dal controllo degli impianti industriali ai piloti automatici degli aerei, al controllo dei missili teleguidati. La circolazione dell'informazione, tipica dei sistemi a retroazione, può comportare nella catena di reazione complesse forme di elaborazione, a volte effettuate in tempo reale da calcolatori elettronici.

Si noti che gran parte delle attività umane è regolata da meccanismi di reazione: la semplice operazione di prendere un oggetto con la mano comporta un meccanismo di retroazione sui muscoli motori da parte dell'informazione visiva elaborata dal cervello; quest'ultimo, istante per istante, fornisce il segnale di errore determinato dalla situazione spaziale mano-oggetto.

La scienza dell'automatica ha recentemente allargato i suoi orizzonti e ha fornito il punto di partenza (e importanti metodi di analisi e di sintesi) per lo sviluppo della ‛scienza dei sistemi' in cui si considerano le modalità di regolazione e di autoregolazione di grandi sistemi, meccanici, economici, sociali, in base alle informazioni accessibili sul loro stato e alle possibili modalità di intervento (controllabilità dei sistemi).

11. Modulazione e demodulazione

Per la trasmissione di segnali conviene spesso trasferire un segnale dalla sua banda di frequenza originaria a un'altra (modulazione); il processo inverso avviene in ricezione dove si ricostruisce, dal segnale modulato, il segnale originario (demodulazione). Storicamente questo trasferimento del segnale in una banda diversa da quella originaria è stato richiesto dalla necessità di trasmettere informazioni mediante onde radio: in quel caso si trattava di affidare il segnale da trasmettere, generalmente a bassa frequenza, come il segnale telefonico, a un'onda portante a radiofrequenza mediante, appunto, un processo di modulazione.

I tipi fondamentali di modulazione di un'onda sinusoidale sono quelli di ampiezza e di fase: se il segnale d'informazione da trasmettere (segnale modulante) è rappresentato dalla funzione s(t), e la portante sinusoidale non modulata è cos(ω_pt+ϕ_p), i due tipi di modulazione sono definiti dalle seguenti formule, rispettivamente per la modulazione d'ampiezza e per quella di fase:

m_a(t)=s(t) cos(ω_pt+ϕ_p); (8)

m_῍(t)=cos[ω_pt+ϕ_p+ϕ(t)]. (9)

Nella (9) relativa alla modulazione di fase, se ϕ(t)=ks(t), si ha la modulazione di fase propriamente detta, mentre, se ϕ(t)=k∫s(t), si ha la modulazione di frequenza: quest'ultima denominazione deriva dal fatto che in questo caso lo scarto della frequenza istantanea f(t) rispetto alla frequenza della portante f_p è proporzionale al segnale s(t). (Si ricorda al riguardo che, per una generica onda rappresentata da cos x(t), viene definita come pulsazione istantanea la derivata x′(t) dell'argomento x(t). Di conseguenza, nel caso dell'onda m_῍(t)=cos[ω_pt+ϕ_p+k∫s(t)dt], la pulsazione istantanea è ω(t)=ω_p+ks(t) e questo mostra la suddetta relazione di proporzionalità).

Un altro tipo di modulazione è quello, illustrato nel cap. 4, ottenuto mediante il campionamento del segnale s(t) che viene sostituito da una successione di suoi campioni aventi spaziatura T₀≤1/2f₀. Come si è visto (v. fig. 6), lo spettro di questo segnale è la ripetizione dello spettro originario di s(t) centrato attorno alle frequenze nf₀=n/T₀ (con n=1,2...). Se la banda B=f_c è tale che 2B≤1/T_o, un opportuno filtro passa-banda centrato attorno alla frequenza nf₀=n/T₀ e con banda passante eguale a f_c, e quindi minore o uguale a f₀/2, alimentato dal segnale campionato, attua una modulazione che trasla lo spettro originario, centrandolo attorno alla frequenza nf₀; si raggiunge così lo stesso risultato che si otterrebbe modulando direttamente in ampiezza una portante sinusoidale di frequenza nf₀. Infatti l'analisi del segnale con modulazione di una portante sinusoidale (formule 8 e 9) mostra che il segnale stesso viene a interessare una banda di frequenze centrata rispetto a ω_p e di larghezza dipendente, in modo diverso secondo il tipo di modulazione, dalla banda del segnale modulante s(t) (v. fig. 25).

Va esplicitamente notato che la modulazione è un'operazione non lineare: per esempio la modulazione d'ampiezza e quella a campionamento, di cui abbiamo parlato, si ottengono come risultato dell'operazione prodotto del segnale modulante s(t) per un segnale sinusoidale sen(ω_pt+ψ), nel primo caso, e, nel secondo, per un segnale periodico

che rappresenta una sequenza di impulsi unitari equispaziati.

In base alla (8) un sistema di trasmissione con modulazione di ampiezza può essere attuato come nella fig. 26: il modulatore e il demodulatore sono due moltiplicatori; per il funzionamento del demodulatore è richiesta in ricezione una oscillazione perfettamente coerente con la portante di trasmissione, o, più precisamente con la portante di trasmissione sfasata dell'ammontare corrispondente al ritardo introdotto dal sistema di trasmissione (tra modulatore e demodulatore). Se si suppone che al segnale si sovrapponga, prima della demodulazione, un disturbo con densità spettrale di potenza h costante, si trova che il rapporto rumore-segnale R_u all'uscita del demodulatore (definito come rapporto fra la potenza del rumore che cade nella banda del segnale e la potenza del segnale stesso) è identico a quello R_i all'entrata del demodulatore (con la convenzione che anche all'entrata del demodulatore la potenza del rumore venga misurata in una banda eguale a quella del segnale modulante). Questo significa che in un sistema di trasmissione ideale (avente attenuazione indipendente dalla frequenza e densità spettrale di potenza del rumore pure indipendente dalla frequenza) non si ha alcuna differenza di prestazione fra il trasmettere il segnale in ‛banda base' (e cioè senza trasportarlo in un intervallo diverso di frequenze) e il trasmetterlo modulando in ampiezza un'opportuna portante. Quando invece della modulazione di ampiezza si consideri quella di fase, si ha

essendo Φ_e la deviazione quadratica media di fase. Se questa è maggiore di 1 si ha un miglioramento nel rapporto rumore-segnale fra entrata e uscita del demodulatore. Questo vantaggio è ottenuto a spese della maggiore banda occupata dal segnale modulato in fase. Come indicato anche dalla formula di Shannon, tutti i sistemi di modulazione (o codificazione) efficienti ottengono un miglioramento nel rapporto rumore-segnale a spese della banda occupata. Dispositivi con tubi elettronici e transistori (v. elettronica), oltre che per la funzione di amplificatori lineari, si prestano, se inseriti in opportuni circuiti, anche per effettuare le operazioni non lineari richieste per la modulazione e la demodulazione.

12. Sistemi di trasmissione

I sistemi per la trasmissione a distanza dei segnali sono costituiti da un appropriato mezzo trasmissivo cui vengono associate apparecchiature elettroniche intermedie e terminali.

Si è già detto che il problema fondamentale dei sistemi di trasmissione è quello di rendere il segnale a distanza in modo economico e con un ammontare di disturbo tollerabile. Si è in particolare accennato (v. sopra, cap. 7) a due tipi fondamentali di disturbi: disturbi additivi indipendenti (in particolare rumore termico ed elettronico) e distorsioni (distorsioni spettrali e distorsioni armoniche). Anche nel presente capitolo verranno considerati solo questi disturbi, trascurando per semplicità la presenza di interferenza, ciò che in realtà è lecito soltanto quando si usino mezzi trasmissivi schermati (linee coassiali, guide d'onda) e collegamenti a microonde altamente direttivi e opportunamente configurati.

a) Sistema con una sola tratta.

Si supponga inizialmente che il sistema di trasmissione sia costituito da una sola tratta (v. fig. 27A) e cioè da un mezzo trasmissivo di una certa lunghezza cui siano collegate apparecchiature terminali di trasmissione e di ricezione. Nella figura si è indicato con n_g(t) il rumore uscente dal mezzo trasmissivo, la cui densità spettrale di potenza h_ng è definita dalla temperatura di rumore T_g del generatore equivalente all'uscita del mezzo trasmissivo, e con n_a(t) il rumore generato nel ricevitore, riportato all'ingresso di quest'ultimo, con la procedura seguita nella definizione di temperatura equivalente di rumore T_a di un amplificatore (v. elettronica, cap. 5). Assumeremo per semplicità che T_g e T_a siano costanti con la frequenza nella banda B_c del segnale ricevuto, benché tale assunzione non sia molto realistica quando il segnale ha banda relativa grande (e cioè è grande il rapporto tra frequenza massima e frequenza minima).

In linea di principio si può pensare di suddividere il trasmettitore e il ricevitore in due parti, come indicato nella fig. 27B; nel trasmettitore si ha innanzitutto un'apparecchiatura per la codificazione (e/o modulazione) dei segnali da trasmettere, che nei casi più completi può includere un sistema per la riduzione di ridondanza (o codificazione della sorgente) e un sistema per la codificazione di trasmissione (e/o modulazione) efficiente nei riguardi dei disturbi di trasmissione (v. fig. 15). Un'apparecchiatura atta a svolgere le operazioni inverse, cioè la decodificazione (e/o demodulazione) costituisce l'ultima parte del ricevitore.

Facciamo l'ipotesi, comoda per la trattazione successiva, che l'apparecchiatura di decodificazione venga definita effettuando il sezionamento r in un punto in cui la densità spettrale di un rumore sia costante; questo comporta nelle nostre assunzioni che sia costante con la frequenza l'amplificazione A_R. (Tale amplificazione sarà, inoltre, sufficientemente elevata così che le sorgenti di rumore presenti nel decodificatore possano trascurarsi). Assumiamo poi che le apparecchiature di codificazione (e/o modulazione) e di decodificazione (e/o demodulazione) siano costruite per funzionare correttamente anche quando connesse direttamente l'una con l'altra (per esempio a scopo di prova). Con queste ipotesi, il sistema fra i terminali t e r deve comportarsi, in tutta la banda B_c del segnale codificato, come un sistema lineare ideale (v. fig. 2) con attenuazione zero e con rumore con densità spettrale costante. Poiché il mezzo trasmissivo ha in generale attenuazione α_t variabile con la frequenza e fase che si scosta dall'andamento ideale proporzionale alla frequenza, il requisito che il sistema fra t e r sia ideale con attenuazione zero impone che il complesso degli amplificatori di trasmissione e di ricezione eguagli le caratteristiche del mezzo trasmissivo. Mentre l'equalizzazione di fase può essere più o meno arbitrariamente distribuita fra trasmettitore e ricevitore, l'equalizzazione dell'attenuazione, che si esprime con la relazione

A_T(f)+A_R=α_t(f), (11)

va invece distribuita tenendo conto del rumore additivo. Se P_r=P_t è la potenza di segnale prefissata in r e per il corretto funzionamento del demodulatore-decodificatore occorre in r un rapporto rumore-segnale R_r=P_nr/P_r non superiore a R_rm, si deve avere in condizioni limite P_nr=P_rR_rm, ossia:

k(T_g+T_a)B_se^2AR=P_rP_rm, (12)

la quale fissa l'amplificazione di ricezione A_R e quindi in base alla (11) quella in trasmissione A_T(f) una volta che T_g+T_a sia noto (come nel caso dei sistemi di modulazione - v. sopra, cap. 11 - la potenza di rumore all'entrata del demodulatore-decodificatore viene convenzionalmente misurata in una banda pari alla banda B del segnale originario non codificato). Se la densità spettrale di potenza del segnale in r è h_r(f)=h_t(f), l'analoga densità in R è h_R(f)=h_r(f)/e^2AR e perciò la potenza che l'amplificatore di trasmissione dev'essere in grado di erogare è

avendo indicato con h_t0(f)=h_r(f)/P_r=h_t(f)/P_t la densità spettrale normalizzata del segnale codificato. Poiché la potenza necessaria in trasmissione è, al di sopra di un certo valore, uno dei fattori più importanti, è interessante sottolineare nella (13) che, poiché detta potenza è inversamente proporzionale al rapporto rumore-segnale in ricezione, è opportuno lavorare (con adeguati margini di sicurezza) nelle condizioni di massimo rapporto rumore-segnale tollerabile, come sopra ipotizzato. Conviene inoltre rendere più bassa possibile la temperatura T_g+T_a•T_g è quasi sempre un dato del problema, T_a dipende invece (v. elettronica, cap. 5) dalla scelta e dal progetto dell'amplificatore di ricezione. Se per quest'ultimo è possibile prendere anche in considerazione amplificatori speciali come quelli parametrici (v. elettronica, cap. 9), è da tenere in conto che il loro costo è elevato e quindi la scelta di P_T e T_a (a parità di α_t) non può che discendere da un'ottimizzazione economica. Non vi è comunque convenienza a ridurre T_a molto al di sotto di T_g, per cui la convenienza di usare amplificatori speciali è praticamente limitata ai sistemi spaziali, in relazione al basso valore di T_g ottenibile da un'antenna puntata verso il cielo (v. fig. 13).

Passiamo ora a considerare, nella (13), l'influenza di α^t e cioè dell'attenuazione del mezzo trasmissivo.

Nella trasmissione su linee (bifilari o coassiali) l'attenuazione è una funzione della frequenza rapidamente crescente (più precisamente è proporzionale alla radice quadrata della frequenza; v. sopra, cap. 6) cosicché si ha interesse a trasmettere i segnali nella zona di frequenze più basse; in questo modo peraltro l'attenuazione del mezzo varia notevolmente nella banda del segnale e l'amplificazione deve provvedere a una forte esaltazione delle componenti a frequenze elevate. Nei sistemi a microonde, invece, la banda occupata dal segnale è sempre piccola rispetto alla frequenza centrale, cosicché sia nel caso di trasmissione con onde irradiate, sia in quello di trasmissione con onde guidate, l'attenuazione può considerarsi costante con la frequenza entro la banda del segnale. In questo caso l'amplificazione di trasmissione e quella di ricezione sono costanti con la frequenza.

Nella (13) compare il rapporto massimo accettabile R_rm fra potenza di rumore e potenza di segnale nel punto r. Si deve osservare che in realtà R_rm non è un dato del problema, poiché il progettista è in grado di scegliere il sistema di codificazione-modulazione. Il vero dato è il massimo rapporto rumore-segnale R_u accettabile all'uscita del sistema e cioè all'uscita del decodificatore-demodulatore; tale rapporto, opportunamente definito, rappresenta infatti i requisiti di qualità per il segnale reso all'utente. Poiché il rumore uscente è, almeno per una frazione η, dipendente dal rumore entrante, si può scrivere

R_r=f(ηR_u), (14)

in cui f(ηR_u) dipende dal metodo di codificazione adottato. (Mentre la frazione ηP_nu del rumore uscente P_nu dipende, come ipotizzato, dal rumore additivo in ricezione, la frazione (1-η)P_nu è dovuta essenzialmente ai contributi di disturbo delle apparecchiature di codificazione e di decodificazione; è particolarmente importante, per questo aspetto, il caso in cui il codificatore trasformi un segnale analogico in un segnale numerico; il rumore (1−η)P_nu è in tal caso il rumore di quantizzazione - v. sopra, cap. 3 - che è deliberatamente introdotto nel processo di codificazione allo scopo di rendere grande la funzione f(ηR_u), ossia di rendere il segnale codificato meno sensibile al rumore dovuto alla trasmissione). In queste condizioni la (13) diventa:

La (15) mette in evidenza i vantaggi di usare un metodo di modulazione o codificazione efficiente che consenta di operare, a parità di R_u, con un R_r all'ingresso del decodificatore-demodulatore più elevato (alto valore di f(ηR_u)); d'altra parte questo vantaggio viene ottenuto, nei metodi di codificazione efficienti, con un aumento di B_c che non è sempre accettabile, sia perché la banda può essere una risorsa preziosa (come può accadere nelle radiotrasmissioni), sia perché, se α_t cresce rapidamente con la frequenza, l'integrale a secondo membro della (15) cresce al crescere di B_c. Vantaggi anche nei riguardi della banda possono ottenersi usando nel codificatore una riduzione di ridondanza (codificazione della sorgente) prima di provvede- re alla codificazione di trasmissione, ma ciò crea complicazioni nelle apparecchiature, il cui costo va messo ovviamente in conto.

All'estremo opposto delle complicazioni citate è il caso di trasmissione diretta, in cui il segnale viene trasmesso senza alcuna modulazione o codificazione (v. fig. 28). In luogo delle apparecchiature di modulazione e codificazione si hanno semplicemente delle apparecchiature lineari aventi lo scopo eventuale di far assumere allo spettro di rumore uscente l'andamento più opportuno ai fini ad esempio di rendere minima la potenza trasmessa. (Ciò implicherà un certo andamento della funzione h_r(f) e quindi di h_t(f)).

Le considerazioni che si possono fare sulla trasmissione diretta valgono anche per la trasmissione con modulazione d'ampiezza, per quanto detto nel cap. 11.

Come esempio di applicazione delle considerazioni svolte si può prendere quello di una sonda spaziale che debba trasmettere dati scientifici rilevati nello spazio profondo. In questo caso si ha grandissimo vantaggio a ridurre la potenza di trasmissione poiché un trasmettitore potente contribuisce grandemente alla massa del veicolo che a sua volta determina il costo del lancio. È quindi necessario ridurre i vari fattori a secondo membro della (15), facendo anche ricorso ad apparecchiature di terra molto costose, poiché questi costi additivi vanno comparati con gli elevati costi additivi che si avrebbero altrimenti nella costruzione del veicolo. Se la trasmissione si effettua a frequenze inferiori a 10 GHz la propagazione avviene all'incirca come nello spazio libero (v. sopra, cap. 6) e si ha:

in cui G_t è il guadagno dell'antenna trasmittente, dovuto alla concentrazione del fascio irradiato rispetto al caso di radiazione uniforme in tutte le direzioni, e A_r è l'area equivalente di captazione dell'antenna ricevente. La (15) diventa:

Il guadagno dell'antenna di bordo G_t è limitato dalle dimensioni dell'antenna e dalla precisione del suo puntamento verso terra.

Un esempio in proposito è dato dal Mariner inviato nel 1973 a esplorare Venere e Mercurio (v. fig. 29).

L'antenna trasmittente ha in questa sonda un guadagno di 360 (25,6 dB) (cui corrisponde un'apertura di ±4°) alla frequenza di lavoro di circa 2,3 GHz; si può contare su una precisione di puntamento di circa 2° e, nelle condizioni peggiori, su un guadagno di 275.

Per l'antenna di terra si è invece adottato un paraboloide della stazione della NASA a Goldstone (California). Si tratta di un paraboloide con diametro di 64 m, cui corrisponde un'area equivalente di circa 1.700 m². Quest'ultima antenna ha il vantaggio di una bassa temperatura equivalente di rumore T_g (circa 40 °K con angolo di elevazione di 10°).

Si è potuto quindi usare con vantaggio un amplificatore di ingresso al ricevitore di tipo maser, con temperatura di rumore T_a=15 °K. Il segnale da trasmettere è un segnale visivo: si tratta infatti di fotografie della superficie di Mercurio. Il metodo di modulazione prescelto è di tipo numerico: la fotografia è definita da 704×945 punti, di ciascuno dei quali si può trasmettere la luminanza in 256 livelli di grigio dal nero al bianco. Ciò significa la trasmissione di 8 simboli binari per punto e quindi di 5•10⁶ simboli binari per fotografia. Il disturbo complessivo è costituito dal disturbo di quantizzazione, dovuto al numero finito dei livelli di grigio trasmissibili, che non dipende pertanto da R_r, e dal disturbo dovuto alla trasmissione, proporzionale alla probabilità di errore che dipende da R_r. Se non si effettuasse alcuna codificazione speciale ma si trasmettessero soltanto i vari simboli binari ottenuti dal segnale, con pura modulazione d'ampiezza (per esempio ampiezza A per il simbolo 1, ampiezza −A per il simbolo 0), la probabilità d'errore sarebbe data dalla fig. 30 in funzione del rapporto all'entrata fra energia per simbolo e metà della densità spettrale di rumore.

In realtà nella sonda considerata si utilizza un codice che dà una probabilità di errore di 5•10^-3 con un rapporto fra energia per bit e densità spettrale di rumore pari a 2 (3dB), con un vantaggio di 2,2dB rispetto alla trasmissione senza codifica. Ciò significa che deve aversi R_r=2/T essendo T l'intervallo intercorrente fra i simboli, ossia 1/T la frequenza di cifra. Introducendo nella (17) i vari valori citati e per l la distanza da Mercurio, si ottiene:

Nel Mariner la potenza utile in trasmissione è 8,3 W, col che la (18) fornisce T=2,18•10^-4 s, 1/T=4.600 bit/s. (In realtà, l'intervallo tra i simboli è stato assunto di 2,47•10^-4 s). Il sistema può quindi trasmettere una fotografia in circa 22 minuti. Dalla formula (5) di Shannon sappiamo d'altra parte che con un'espansione di banda infinita si potrebbero trasmettere senza errori, con la stessa potenza, C=13.000 bits al secondo. Confrontando questo numero col precedente si può dedurre il vantaggio conseguibile con una codificazione ottima.

b) Sistemi con più tratte.

In pratica si ha assai frequentemente a che fare con collegamenti appartenenti a una rete di comunicazione. Per esempio, la rete telefonica mondiale è costituita da un insieme assai complesso di collegamenti che, attraverso centri di commutazione di vario rango, consentono di congiungere fra loro due utenti qualsiasi. Ne consegue che un collegamento effettivo è costituito in genere da più collegamenti in cascata (v. fig. 31).

Si assuma che i vari collegamenti presi isolatamente diano luogo ai rapporti rumore-segnale R_uA=P_nuA/P_uA, R_uB=P_nuB/P_uB, ecc., rispettivamente nei punti A, B, ...; si connetta A con A′, R con B′ ..., facendo sì che le potenze di segnale immesse in A′, B′, ... restino eguali a quelle che erano originariamente immesse nei collegamenti isolati. Il segnale uscente in B avrà ancora potenza P_uB, mentre, se i contributi di rumore dei singoli collegamenti sono fra loro incorrelati, la potenza del rumore in B sarà P_nuBA+P_nuB, in cui P_nuB è la potenza di rumore propria del collegamento A′B (quella già presente nel collegamento isolato) e P_nuBA è la potenza di rumore del collegamento 0A trasferita in B. Il rapporto rumore-segnale complessivo in B sarà:

essendo l'ultima eguaglianza dovuta al fatto che, nel passaggio da A a B, sia il segnale che il rumore subiscono la stessa amplificazione.

In generale per un sistema di k collegamenti in cascata si ha:

Se dunque il requisito di qualità, che deve essere soddisfatto sul collegamento della massima lunghezza possibile l_o, richiede un certo rapporto R_u0, occorrerà che i rapporti rumore-segnale dei singoli collegamenti siano tali che la loro somma non superi R_u0. Ciò conduce, almeno sui collegamenti a grande distanza, a richiedere che il rapporto rumore-segnale sia proporzionale alla lunghezza e precisamente che su un collegamento di lunghezza generica l si abbia

(Si osservi che alla (19) si è pervenuti assumendo che ogni tratta sia in generale costituita nel modo completo indicato in fig. 27B e che il rumore P_nu sia tutto generato nelle varie tratte considerate. Se così non fosse, e cioè si avesse una parte di rumore associata al segnale che non si va accumulando di tratta in tratta, la formula (19) resterebbe tuttora valida nei riguardi del solo rumore che si va accumulando; per esempio, se il codificatore include un convertitore di segnale analogico in segnale numerico, è inutile ripetere in ogni tratta il passaggio analogico-numerico e viceversa producendo ogni volta rumore di quantizzazione; basta fare l'operazione una sola volta rispettivamente all'inizio e alla fine del collegamento, in modo che il rumore di quantizzazione non si accumuli più. Con le notazioni del punto precedente soltanto una frazione del rumore uscente sarà dunque dovuta all'accumulo da parte delle varie tratte).

In queste condizioni la formula (15) relativa alla potenza da trasmettere su un collegamento di lunghezza l si modifica come segue:

Si applichi innanzitutto questa formula a un collegamento con trasmissione diretta, o con modulazione di ampiezza, per il quale si abbia, in fig. 28, H(f)=costante e quindi sia f(x)=x. La (21) diventa:

dalla quale si ricava che in tutti i casi pratici la P_T risulta una funzione crescente di l; a maggior ragione ciò accade nel caso più generale in cui debbasi applicare la (21), poiché con i sistemi di codificazione efficiente la f(x) varia con x in modo, anche notevolmente, più lento che nel caso di semplice proporzionalità. Dalla fig. 30 per esempio si ricava che la probabilità d'errore e quindi la potenza del rumore dovuto agli errori (rumore di trasmissione) decresce circa esponenzialmente al crescere del rapporto segnale-rumore all'ingresso. Quindi, per ottenere un certo rapporto segnale-rumore all'uscita di un collegamento di lunghezza totale l₀, può essere conveniente, o addirittura indispensabile, spezzare il collegamento in tratte parziali di lunghezza l, poiché ciò riduce la potenza necessaria sulla singola tratta; quest'effetto è particolarmente sentito con i mezzi trasmissivi con propagazione guidata, per i quali la potenza varia all'incirca esponenzialmente con la lunghezza (v. sopra, cap. 6). Per i motivi visti, i collegamenti a grande distanza con onde guidate sono tutti ottenuti con molte tratte, essendo le tratte tanto più brevi quanto più è forte l'attenuazione per unità di lunghezza.

Nell'importante esempio dell'uso di linee coassiali le tratte sono tanto più brevi quanto più sono alte le frequenze in gioco.

Nel caso di trasmissione telefonica, i singoli canali telefonici vengono affiancati in frequenza (trasmissione multipla a divisione di frequenza) mediante modulazione di ampiezza con banda laterale unica. La banda assegnata a ciascun canale è 4 kHz così che la banda occupata sarebbe teoricamente 4N kHz, se N è il numero dei canali. In realtà la banda è più grande perché, per comodità di attuazione delle apparecchiature, i canali vengono riuniti in gruppi d'ordine sempre maggiore e adeguatamente separati in frequenza in modo da facilitarne il prelievo mediante filtri. Inoltre la frequenza minima viene tenuta a un valore tale che il rapporto tra frequenza massima e frequenza minima non sia troppo elevato.

Attualmente sulle linee coassiali con diametro di 9,5 mm sono in servizio sistemi che trasmettono 960 canali telefonici (frequenza massima 4 MHz) per coppia coassiale, con tratte lunghe 9 km. (Una coppia coassiale serve per i due sensi di trasmissione: si hanno cavi con 2 coppie e cavi con molte coppie, per es. una decina). Vi sono poi sistemi che trasmettono 2.700 canali telefonici (frequenza massima 12 MHz) per coppia coassiale, con tratte lunghe 4,5 km; infine sono stati sviluppati, con alcune prime installazioni, sistemi per 10.800 canali (frequenza massima 60 MHz) per coppia coassiale, con tratte lunghe 1,5 km.

È da notare che i sistemi considerati possono trasmettere in ciascun canale telefonico anche segnali telegrafici o dati; si possono anche sostituire, a gruppi di canali telefonici, segnali numerici ad alta velocità.

Per avere qualche idea più quantitativa dei parametri in gioco si consideri che la linea coassiale da 9,5 mm attenua alla massima frequenza usata nel sistema a 10.800 canali circa 18 dB/km, ossia 27 dB sulla tratta di 1,5 km. Poiché su un percorso di qualche migliaio di chilometri l'attenuazione raggiunge, alla predetta frequenza, decine di migliaia di decibel, dev'essere mantenuta molto precisa l'amplificazione che deve compensare quest'attenuazione entro detti limiti, anche in presenza di variazioni di attenuazione dovute a variazioni di temperatura (l'attenuazione cambia del 2‰ per grado centigrado).

Le apparecchiature di linea, che si trovano fra una tratta e l'altra, sono dunque amplificatori controllati; detti amplificatori corrispondono all'amplificatore di ricezione e a quello di trasmissione della fig. 27B, messi fra loro in cascata.

La linea coassiale viene oggi prevista anche per trasmissioni in forma numerica. Se, come spesso accade, il segnale di tipo numerico deriva da un segnale originariamente analogico, si hanno, come già più volte ricordato, due tipi principali di disturbo: il rumore di quantizzazione e il rumore dovuto agli errori di trasmissione. Generalmente si attribuisce quasi tutto il rumore totale al rumore di quantizzazione, poiché una riduzione del rumore di quantizzazione richiede un aumento del numero di cifre binarie per campione e quindi una complicazione maggiore delle apparecchiature e una maggiore larghezza di banda; la riduzione del rumore dovuto agli errori è invece ottenibile con piccolo aumento della potenza trasmessa (v. fig. 30). Come si è già messo in evidenza, dovendosi fare un collegamento a più tratte, il rumore dovuto agli errori di trasmissione si accumula di tratta in tratta (formula 21), mentre il rumore di quantizzazione si accumula soltanto quando si fa la conversione analogico-numerica e quella inversa.

La soluzione preferibile sarebbe quella di quantizzare una volta per tutte all'inizio del collegamento e fare l'operazione inversa soltanto all'arrivo. Ma ciò sarà realizzabile solo quando si potrà effettuare qualsiasi percorso in forma numerica; questa possibilità, se pur rappresenta una delle attuali tendenze, è ancora lontana, cosicché un percorso completo è in generale ottenuto mediante successioni di trasmissioni analogiche e di trasmissioni numeriche. Per tale motivo il numero di cifre binarie per campione viene scelto superiore a quello che sarebbe necessario per una trasmissione numerica integrale. In particolare in telefonia si usano, come si è detto, 8 cifre binarie per campione contro le 6 o 7 che sarebbero necessarie se si quantizzasse una sola volta.

Se si lascia alle sole apparecchiature terminali il compito di effettuare le operazioni di codificazione e di decodificazione, il sistema di trasmissione vero e proprio viene a essere semplicemente un sistema per la trasmissione, con un certo tasso d'errore massimo, di un segnale numerico avente una certa velocità (in simboli binari al secondo). Lo schema delle apparecchiature di linea è illustrato nella fig. 32. È importante avere in ogni apparecchiatura intermedia lungo la linea i circuiti per la decisione e la rigenerazione del segnale numerico perché, se si provvedesse a una semplice amplificazione eliminando il rigeneratore, si sommerebbero lungo la linea i rapporti R_r anziché i rapporti R_u e si dovrebbe scrivere, invece della (21), la seguente:

che darebbe un risultato identico alla (21) solo se fosse f(x)=x; poiché in realtà la f(x) varia con x più lentamente, la potenza richiesta dalla (23) sarebbe molto maggiore di quella richiesta dalla (21).

Si è già detto come l'espansione di banda, e in particolare quella ottenuta con una trasmissione numerica binaria, che per un verso migliora la funzione f(x), rechi invece svantaggi a causa dell'attenuazione rapidamente crescente con la frequenza (nell'integrale a secondo membro della formula). Per tale motivo potranno essere prese in considerazione sulle linee coassiali trasmissioni con numerazione di ordine superiore al binario (per es. trasmissione quaternaria).

L'adozione della trasmissione numerica sulle linee verrà probabilmente fatta non per motivi di vantaggio nella potenza (o nella lunghezza di tratta), ma perché il segnale numerico può essere facilmente elaborato, può rappresentare qualsiasi tipo di segnale, si presta particolarmente bene a essere trasmesso sui mezzi trasmissivi del futuro (ponti radio a frequenza elevatissima, guide d'onda, fibre ottiche) e consente la multiplazione a divisione di tempo e la commutazione a divisione di tempo (v. sotto, È c). Nel sistema a divisione di tempo i segnali vengono trasmessi in forma campionata e l'intervallo corrispondente a un periodo di campionamento viene suddiviso fra gli N segnali che si vogliono trasmettere, assegnando loro intervalli di tempo adiacenti. Si presta particolarmente bene allo scopo la trasmissione dei campioni in forma numerica, poiché in questo caso si ottiene una notevole protezione del segnale dalla deformazione degli impulsi causata da distorsioni spettrali. Nel caso comune di trasmissione telefonica, che usa 8 simboli binari per campione a una frequenza di campionamento di 8•10³, la velocità di cifra teorica del segnale multiplo è evidentemente 64N•10³ simboli binari al secondo. Nel caso di 10.800 canali telefonici (la capacità già vista per la trasmissione in forma analogica), la velocità risulterebbe dunque di poco inferiore a 10⁹ simboli binari per secondo e cioè al limite dell'attuale tecnologia elettronica.

Per chiudere l'argomento della trasmissione su linea coassiale occorre infine menzionare lo sviluppo che hanno avuto i sistemi in cavo sottomarino dopo che l'evoluzione della tecnica ha permesso l'adozione di amplificatori sommersi.

Il primo sistema telefonico transatlantico in cavo è del 1956 con un cavo per ciascuna direzione; esso poteva tra- smettere 36 canali telefonici nei due sensi con amplificatori a tubi elettronici spaziati di circa 67 km. Attualmente si dispone di sistemi sottomarini in cavo con capacità di trasmissione di 845 canali telefonici e amplificatori a transistori spaziati di 18 km. Nel cavo sottomarino (come in quello terrestre) l'adozione del transistore è stata vantaggiosa non solo per l'affidabilità ma anche per il consumo di potenza (gli amplificatori debbono essere telealimentati, esclusivamente dalle estremità, dallo stesso cavo usato per la trasmissione).

Nel campo della trasmissione guidata, la guida d'onda nel modo TE₀₁ (v. fig. 7C) sembra di prossimo uso commerciale. La guida è caratterizzata da un'attenuazione molto bassa e non molto variabile nella gamma da 30 a 100 GHz circa. L'enorme larghezza di banda disponibile e la presenza di distorsioni spettrali dovute alla propagazione a molti modi, rendono la trasmissione di tipo numerico particolarmente adatta a questo mezzo trasmissivo. Si prevede l'uso di più onde portanti ciascuna modulata da un segnale numerico ad altissima velocità, per esempio dell'ordine di 10⁹ simboli binari al secondo, come si è precedentemente accennato in questo stesso paragrafo. La capacità complessiva di una guida d'onda del tipo menzionato può pertanto essere dell'ordine di varie centinaia di migliaia di canali telefonici; a poco più di un migliaio di canali telefonici può sostituirsi un canale televisivo.

Nelle guide d'onda si trae partito dalla disponibilità di componenti allo stato solido capaci di generare potenza alle onde millimetriche (v. elettronica, capp. 10 e 12): è previsto un passo di ripetizione di circa 20 km.

Grande interesse pratico si prevede pure per le trasmissioni a frequenze luminose in fibra ottica.

Accanto ai sistemi di trasmissione su onde guidate, vanno considerati i sistemi con onde irradiate. Essi sono evidentemente gli unici possibili nelle comunicazioni con mezzi mobili; ma anche per i collegamenti fra punti fissi offrono soluzioni molto convenienti.

Come si è già detto nel cap. 6, le onde con frequenza inferiore a circa 30 MHz offrono la possibilità di collegamenti anche a grande distanza fra punti a terra non in visibilità, ma permettono di trasmettere bande modeste.

Alle frequenze più elevate, che offrono bande assai più grandi, la propagazione può avvenire soltanto fra punti in visibilità, perché al di là dell'orizzonte il segnale si attenua rapidamente con la distanza.

Per tale motivo i collegamenti terrestri a microonde a grande distanza fra punti fissi (ponti radio), che operano attualmente con frequenze fra 1 e 10 GHz, vengono attuati mediante successive tratte in cascata; a differenza peraltro dei sistemi su linea, la potenza necessaria, finché esiste la visibilità fra i terminali, cresce lentamente con la distanza cosicché la lunghezza di tratta viene generalmente spinta al limite della visibilità. Servendosi di torri si possono raggiungere facilmente distanze intorno ai 50 km e, utilizzando rilievi naturali e montagne, sono possibili collegamenti in visibilità su distanze ben maggiori, come il collegamento fra continente e Sardegna che è di circa 240 km. In questi casi peraltro vi sono limitazioni di banda a causa delle distorsioni spettrali dovute ai percorsi multipli nella troposfera. Poiché l'attenuazione di tratta varia nel tempo (con un valore mediano prossimo a quello dello spazio libero), soprattutto a causa dei percorsi multipli di propagazione (v. fig. 12), il progetto deve tenere in conto la statistica dell'attenuazione di tratta, in modo che le interruzioni di servizio o i periodi di servizio insoddisfacente abbiano piccolissima probabilità, praticamente dello stesso ordine di quella dei guasti delle apparecchiature. Gli attuali ponti radio a microonde operano con modulazione angolare (modulazione di fase o di frequenza), trasmettendo segnali televisivi o segnali telefonici multipli a divisione di frequenza.

La modulazione angolare adottata usa piccola deviazione di fase che, pur non offrendo vantaggi nei riguardi del rumore (v. la 10), li offre nei riguardi della costanza del segnale demodulato di fronte alle variazioni dell'attenuazione di percorso, e nei riguardi della sostanziale invulnerabilità del segnale alle distorsioni armoniche. Ciò è particolarmente importante per gli amplificatori di trasmissione (generalmente tubi a onde progressive) che possono lavorare in saturazione.

Le apparecchiature dei moderni ponti radio sono del tipo illustrato nella fig. 33: le apparecchiature intermedie provvedono ad amplificare il segnale trasferendolo a una frequenza più bassa di quella delle microonde per semplificare il problema del filtraggio e agevolare l'attuazione di amplificatori a transistori; inoltre la frequenza di uscita è diversa da quella di entrata allo scopo di evitare i disturbi derivanti dall'accoppiamento fra antenna trasmittente e antenna ricevente.

A seconda dei tipi, i ponti radio di grande capacità attualmente in servizio possono trasmettere su ciascuna onda portante, cioè su ciascun canale radio: a) 960 canali telefonici (o, in alternativa, un canale televisivo); b) 1.800 canali telefonici; c) 2.700 canali telefonici (in questo caso, per es., l'intervallo in frequenza fra i diversi canali radio è di 40 MHz). La fig. 34 illustra appunto la canalizzazione a radio frequenza raccomandata internazionalmente per questi ponti radio: si hanno 8 coppie di canali radio (nella fig. 33 è indicato come una di queste coppie venga usata per attuare un canale radio bilaterale) che possono essere tutte usate sullo stesso ponte radio con le stesse antenne e con differenti apparecchiature per ciascuna coppia.

Il sistema a 2.700 canali può dunque offrire su ciascun percorso 2.700×8=21.600 canali telefonici. In realtà solo 6 canali radio vengono adoperati simultaneamente, mentre i rimanenti 2 vengono tenuti come riserva ‛attiva'. Detta riserva serve sia a far fronte ai guasti delle apparecchiature sia ai più profondi affievolimenti di propagazione, i quali hanno piccolissima probabilità di verificarsi simultaneamente su due diversi canali radio.

Un ponte radio particolare è quello che usa il satellite artificiale come stazione intermedia nello spazio, così da ottenere la visibilità anche con stazioni terrestri a grande distanza. La postazione più conveniente del satellite è quella geostazionaria, ottenibile mediante orbita equatoriale a 36.000 km d'altezza; in questo caso il satellite appare fisso all'osservatore terrestre e il collegamento è assicurato con continuità e con orientamento dell'antenna, tanto più fisso quanto più precisa viene mantenuta la posizione del satellite. Il ponte radio attraverso satellite viene progettato con caratteristiche generali analoghe a quelle dei ponti radio terrestri, salvo le seguenti considerazioni: a) le due tratte che costituiscono il sistema mediante satellite sono enormemente più lunghe, ma hanno il vantaggio che su di esse la propagazione avviene come in spazio libero; b) l'apparecchiatura di bordo deve essere semplice e con la minore potenza possibile, mentre a terra, dove è accettabile una certa complicazione, si usano trasmettitori potenti, grandi antenne e ricevitori con bassissimo rumore.

Poiché tre satelliti distribuiti lungo l'orbita geostazionaria sono sufficienti a coprire l'intera superficie terrestre (escluse le calotte polari), ogni satellite si presta all'attuazione di tutti i collegamenti fra i punti a terra che cadono nella regione di visibilità del satellite; si pone pertanto il problema dell'accesso multiplo al satellite da parte di più stazioni a terra; nei sistemi attuali l'accesso multiplo è ottenuto a divisione di frequenza, nel senso che si hanno diversi canali radio (di varia capacità) assegnati alle singole stazioni.

Recentemente, in aggiunta ai canali radio assegnati in modo permanente alle varie stazioni, è stato introdotto un sistema di assegnazione su domanda; si sono stabilite certe frequenze portanti, ciascuna modulata da un canale telefonico, che vengono lasciate a disposizione generale e attribuite solo quando se ne faccia richiesta. Ciò consente un'assai migliore utilizzazione della capacità disponibile, specie nel caso di stazioni con piccolo traffico, le quali possono richiedere l'assegnazione del canale solo quando giunge una chiamata; naturalmente il sistema è dotato di un controllo che permette un'assegnazione immediata.

Il più recente satellite messo in servizio dall'Intelsat, il Consorzio Internazionale per le Comunicazioni mediante Satelliti, è l'Intelsat IV (v. tavola), che ha una massa in orbita di 750 kg ed è capace di trasmettere, a seconda dei modi di operazione, da 3.000 a 9.000 circuiti telefonici. Attualmente (1974) si hanno due satelliti di questo tipo in servizio sull'Atlantico, uno in servizio sul Pacifico e uno in servizio sull'Indiano.

Nel prossimo futuro è da prevedere un forte aumento di traffico nei sistemi mediante satellite, in relazione non soltanto all'aumento di traffico sui percorsi intercontinentali, ma anche all'applicazione dei satelliti ai servizi ‛regionali'; sistemi di questo tipo sono stati già attuati in Canada e negli Stati Uniti. È previsto anche un sistema preoperativo europeo. In questo tipo di servizio è compresa la distribuzione, e successivamente la diffusione, semidiretta (alle antenne di comunità) o diretta, dei programmi televisivi.

Anche per i collegamenti terrestri a microonde è da prevedere un ulteriore incremento.

In relazione agli sviluppi citati, i problemi relativi ai ponti radio a microonde del futuro, sia terrestri sia mediante satelliti, sono soprattutto i seguenti.

1. Utilizzare nel modo migliore possibile le gamme di frequenza attualmente disponibili: ciò significa sia usare al meglio i canali radio realizzabili su un certo percorso (utilizzando opportuni metodi di modulazione ed eventualmente, quando l'economia lo consenta, metodi di riduzione della ridondanza; per i satelliti è anche importante l'estensione dell'accesso multiplo a domanda), sia riusare il più possibile delle volte le stesse frequenze nell'attuare diversi percorsi; per quest'ultimo aspetto la direttività delle antenne ha un ruolo molto importante e assume caratteristiche di particolare rilievo nel caso dei satelliti, mediante l'introduzione di antenne ‛multifascio' e cioè con molti fasci di captazione e di radiazione, in modo da suddividere la regione servita in varie sub-regioni, ciascuna operante con un fascio che utilizza le stesse frequenze degli altri fasci; al limite, si può pensare di arrivare a utilizzare un fascio molto stretto per ciascuna stazione da servire. La procedura ora indicata consente anche di ridurre al minimo la potenza del satellite, ma richiede a bordo un'apparecchiatura di commutazione simile, in piccolo, a una centrale telefonica (v. sotto, È c), per consentire l'instradamento delle comunicazioni da un fascio agli altri.

2. Utilizzare nuove gamme di frequenza: sono queste le frequenze al di sopra di 10 GHz per le quali si verificano attenuazioni atmosferiche, in particolare dovute alla pioggia. Le caratteristiche statistiche dell'attenuazione da pioggia sono oggetto di ricerche in tutto il mondo; è certo che per i ponti radio terrestri si dovranno usare tratte molto più brevi delle attuali; per i collegamenti con satelliti la situazione è più favorevole, sia perché il tratto che può essere interessato dalla pioggia è più breve relativamente all'intero collegamento, sia perché è più facile in questi sistemi trarre partito dalla limitata estensione dei temporali, predisponendo due o più postazioni a terra in una stessa località e operando con quella non sottoposta a pioggia intensa.

3. Utilizzare metodi di trasmissione di tipo numerico. Anche nei ponti radio la tendenza verso la trasmissione numerica si farà sentire e infatti i ponti radio a frequenze superiori a 10 GHz la utilizzeranno certamente in forma molto estensiva; nei collegamenti mediante satelliti la trasmissione numerica consentirà tra l'altro l'accesso multiplo a divisione di tempo che sfrutta meglio la potenza di bordo, poiché il tubo a onda progressiva finale può essere assai più spinto verso la saturazione.

c) Reti di comunicazione e commutazione

Nella trasmissione a distanza i segnali d'informazione sono destinati a volte a un'intera collettività (distribuzione di segnali fonici e visivi) a volte a specifici utenti. Quest'ultimo è il caso più frequente (telefonia, telegrafia, trasmissione di dati, ecc.) e viene messo in pratica attuando reti di comunicazione cui ciascun utente può connettersi, quando lo desideri, per inviare messaggi a uno qualsiasi degli altri utenti. L'esempio più cospicuo di questa possibilità è rappresentato dalla rete telefonica mondiale, i cui rami sono costituiti dai sistemi di trasmissione oggetto del È b. La determinazione della conformazione di una rete e il dimensionamento dei suoi rami vengono fatti tenendo conto delle correnti di traffico da smaltire. Si tratta di un dimensionamento statistico, fatto in modo da rendere molto piccola la probabilità che una determinata connessione non possa essere effettuata al momento desiderato. Naturalmente di fronte a un traffico rapidamente crescente detto dimensionamento va fatto in funzione delle previsioni del traffico. Nei punti nodali della rete sono predisposti sistemi di commutazione atti a effettuare la connessione nella direzione desiderata. Nel caso della commutazione telefonica, e più in generale nel caso di commutazione ‛di circuito', l'apparecchio dell'utente chiamante deve essere connesso all'apparecchio chiamato per la durata della conversazione. Invece nel caso telegrafico o di trasmissione di dati la commutazione può essere ‛di messaggio'; cioè il messaggio, munito di tutti i dati di indirizzo, può essere memorizzato e successivamente inviato nella direzione voluta appena possibile, con una probabilità preassegnata che il ritardo complessivo di trasmissione non superi un certo valore. Sia nel caso di commutazione di circuito, sia in quello di commutazione di messaggio esisteranno più strade alternative per raggiungere il destinatario e queste andranno progressivamente esaminate dagli organi di controllo con un certo ordine di priorità.

Un esempio di sistema di commutazione di circuito è dato da una centrale telefonica urbana (v. fig. 35). A essa fanno capo linee di utente e giunzioni verso altre centrali. La centrale comprende una rete di commutazione e un sistema di controllo. Quest'ultimo, nelle realizzazioni più moderne, è un elaboratore elettronico. La rete di commutazione usa un insieme di relè capaci di chiudere contatti in opportuni punti di incrocio, come è illustrato nel semplice esempio della fig. 36; si tratta in questo caso di un sistema con M ingressi ed N uscite che può rappresentare in particolare un sistema con M linee (entranti o uscenti) ed N linee interne per consentirne la reciproca connessione (v. fig. 37). In quest'ultimo caso, se N=M/2, la rete si dice ‛non-bloccante' dato che è sempre possibile effettuare la connessione fra due qualsiasi utenti liberi. Una rete non-bloccante è quasi sempre esuberante, se il numero degli utenti è grande e/o il traffico su ogni linea è piccolo. Quest'ultima condizione è sempre verificata per le linee di utenti privati, per le quali, anche nel periodo di massimo traffico, l'occupazione è dell'ordine di qualche percento del tempo. Diversa è la situazione per le linee usate come giunzioni, sulle quali il traffico viene concentrato. (Un concentratore può essere attuato in linea di principio con la rete della fig. 36 in cui si abbiano M linee entranti a basso traffico e N>M linee uscenti a traffico più elevato).

La configurazione della fig. 37, sia per rete bloccante (N>M/2) che per rete non-bloccante (N=M/2), usa, a parità di prestazioni, un numero di incroci molto maggiore di quello strettamente necessario, che è ottenibile mediante configurazioni a più stadi. Un esempio di rete a due stadi è riportato nella fig. 38. In queste configurazioni il numero dei contatti da chiudere per effettuare una certa connessione è notevolmente più grande, ma il numero totale dei punti d'incrocio, ossia dei relè, è molto più piccolo.

Il sistema di controllo della fig. 35 deve ad esempio provvedere alle seguenti operazioni: a) passare in rassegna con sufficiente frequenza tutti gli ingressi di linea alla centrale per determinare le eventuali richieste di servizio (per una linea di utente la richiesta di servizio è determinata dal sollevamento, da parte dell'utente, del microtelefono); b) connettere una memoria alla linea chiamante per riceverne le istruzioni (per es.: numeri composti col disco combinatore); c) esaminare le possibili strade interne per effettuare la connessione nella direzione voluta; d) esaminare se la linea cui ci si deve connettere è libera; e) effettuare la connessione.

Nella sua attività il sistema di controllo deve anche provvedere a inviare e ricevere informazioni sia verso utenti (per es. il segnale punto-linea che dice all'utente che la memoria è stata connessa alla sua linea e che quindi l'utente può comporre il numero desiderato, il segnale di occupato, il segnale di chiamata), sia verso le altre centrali.

Un tipo di rete di commutazione che potrà avere interessanti sviluppi nel futuro è la rete a divisione di tempo. Un semplice schematico esempio è dato dalla fig. 39, analoga alla fig. 37. I relè sono sostituiti da interruttori veloci a semiconduttore, che permettono di sfruttare il principio del campionamento e della multiplazione a divisione di tempo. Si ricorda in proposito che detto principio assicura che la connessione fra due utenti può essere fatta anche non con continuità, ma per brevi intervalli, purché questi si susseguano regolarmente alla frequenza di campionamento (8.000 Hz nel caso della telefonia). Tenendo conto di quanto sopra, lo schema di fig. 39 contiene una sola linea interna che viene messa a disposizione per le varie connessioni in intervalli diversi del periodo di campionamento. Se quest'ultimo è diviso in intervalli, il sistema equivale a quello della fig. 37 con N linee interne. Naturalmente il numero dei punti di incrocio è ridotto a 1/N. Si stanno oggi studiando sistemi integrati di trasmissione e commutazione a divisione di tempo; in questo caso nella centrale, che deve disporre, oltre che di interruttori veloci, anche di memorie, giungono e partono segnali a divisione di tempo; la centrale provvede a inserire i vari campioni (espressi in forma numerica) di un segnale multiplo entrante negli appropriati intervalli di tempo dei segnali multipli uscenti.

bibliografia.

Brillouin, J., Science and information theory, New York 1956.

De Castro, E., Fondamenti di comunicazioni elettriche, Bologna 1967.

Fano, R. M., Transmission of information, Cambridge, Mass.-New York 1961.

Lucky, R. W., Salz, J., Weldom, E. J., Principles of data communication, New York 1968.

Pierce, J. R., La teoria dell'informazione, Milano 1972.

Shannon, C. E., Weaver, W., The mathematical theory of communication, Urbana 1949, 1963² (tr. it.: La teoria matematica delle comunicazioni, Milano 1971).

Wozencraft, J. M., Jacobs, I. M., Principles of communication engineering, New York 1965.