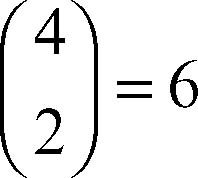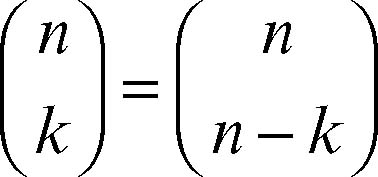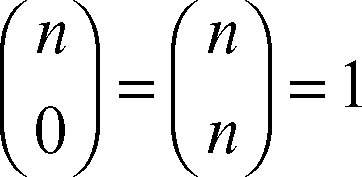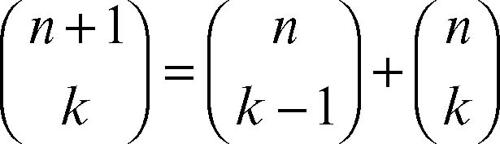Tartaglia, triangolo di
Tartaglia, triangolo di
Tartaglia, triangolo di o triangolo aritmetico o triangolo di Pascal, nel calcolo combinatorio, configurazione triangolare di numeri naturali che fornisce, per ogni valore di due numeri naturali n e k, il valore del coefficiente binomiale
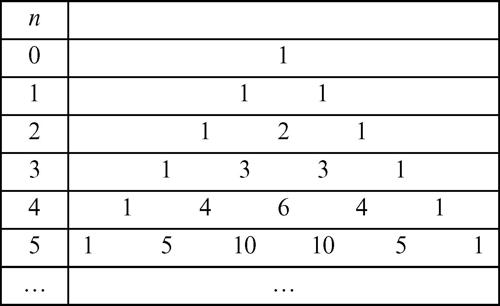
È formato da infinite righe, di cui le prime sono:
Il valore di
è il (k + 1)-simo numero della riga n. Così, per esempio:
perché è il terzo numero sulla riga 4. Vale comunque l’uguaglianza
che indica che in ogni riga i termini equidistanti dagli estremi sono uguali tra loro. Di conseguenza:
L’uguaglianza
indica inoltre che, su ogni riga, ogni termine, esclusi gli estremi che valgono costantemente 1, è pari alla somma dei due termini che si trovano immediatamente sopra di esso.
Il triangolo di Tartaglia fornisce i coefficienti dello sviluppo della potenza n-esima di un binomio (→ Newton, binomio di). È noto anche come triangolo di Pascal perché il filosofo e matematico francese B. Pascal trattò di questo triangolo nel suo Traité du triangle arithmétique.