trigonometria
trigonometria
Dalla scienza dei triangoli alla fisica e alla musica
La trigonometria è quella parte della matematica che si occupa delle relazioni tra lati e angoli in un triangolo. Nacque nell’antichità per viaggiare orientandosi con la posizione del Sole o delle stelle. Successivamente, però, i suoi concetti e strumenti si sono rivelati utili per altri, imprevedibili scopi
Le proprietà del triangolo
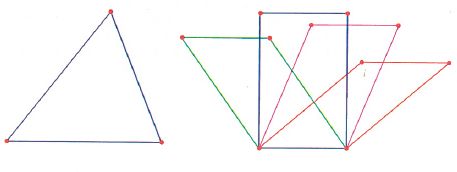
Il triangolo è il poligono con il minor numero di lati ed è fondamentale per lo studio della geometria poiché ogni altro poligono può essere scomposto in più triangoli (v. fig.). Inoltre, il triangolo è indeformabile e infatti, se si inchiodano tre assi, la struttura così realizzata è rigida, mentre una struttura costruita con quattro assi tende a deformarsi, piegandosi lateralmente (v. fig.).
L’indeformabilità del triangolo dipende dalla stretta relazione tra le misure dei suoi lati e quelle dei suoi angoli. Grazie a esse si definiscono le relazioni fondamentali della trigonometria, la branca della matematica che permette di determinare angoli e lati di un triangolo, una volta che ne siano noti alcuni elementi.
Relazioni tra lati e angoli in un triangolo
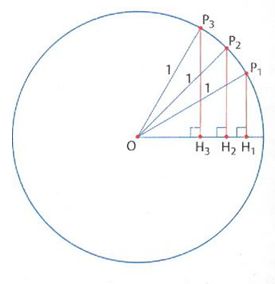
All’interno di una circonferenza di raggio unitario, consideriamo alcuni triangoli rettangoli con ipotenusa di uguale lunghezza, come per esempio i tre triangoli OH1P1, OH2P2, OH3P3 in figura. Se si modifica l’angolo di vertice O, si modifica di conseguenza la lunghezza del cateto opposto.
Si determina così una legge di corrispondenza tra angoli e cateti; per esempio:
HÔP = 30° → HP = H1P1 = 1/2
HÔP = 45° → HP = H2P2 = √2/2 ≈ 0,7071
HÔP = 60° → HP = H3P3 = √3/2 ≈ 0,8660
Il cateto associato all’angolo opposto è chiamato seno dell’angolo. Si dice così, per esempio, che «il seno di 30° è 1/2» e si scrive sen(30°)= 1/2.
Funzioni goniometriche
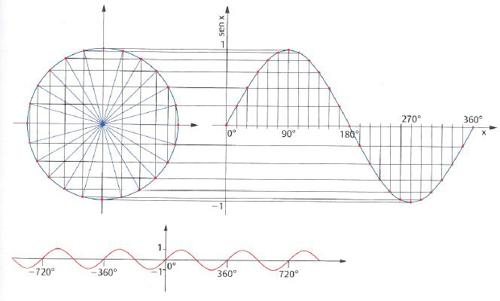
La precedente definizione può essere generalizzata. Considerati tutti i possibili angoli con vertice nel centro di una circonferenza di raggio unitario, si associano a essi i cateti opposti come sono ‘visti’ da tali angoli. Il grafico che mette in relazione questa corrispondenza si costruisce riportando sull’asse orizzontale le diverse ampiezze degli angoli e sull’asse verticale i corrispondenti valori del seno. Si può notare che sen(90°)=1, sen(180°)= 0 e che, quando l’angolo è maggiore di 180° ma minore di 360°, il seno corrispondente è negativo.
Viene così definita una funzione – la funzione seno – che a ogni numero reale fa corrispondere un valore compreso tra 21 e 11. Poiché proviene dalla misura di angoli (gònion in greco), tale funzione è detta funzione goniometrica.
Analogamente è possibile ottenere un’altra funzione goniometrica, quella del coseno, la quale rappresenta la relazione tra l’angolo e il cateto adiacente. Il grafico della funzione goniometrica coseno è ‘spostato in avanti’ – il termine tecnico è traslato – rispetto a quello della funzione seno di una certa quantità lungo l’asse orizzontale.
Per il teorema di Pitagora applicato al triangolo rettangolo che ha qui ipotenusa unitaria, la somma dei quadrati dei cateti, ossia del quadrato del seno e del quadrato del coseno, deve valere 1: questa è una relazione fondamentale della trigonometria.
Funzioni e relazioni trigonometriche permettono di risolvere numerosi problemi geometrici anche di utilità pratica, come rilevare le distanze tra punti inaccessibili o determinare la rotta durante la navigazione.
Dalla geometria alla descrizione di fenomeni fisici
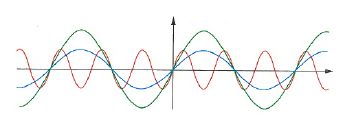
Le funzioni goniometriche, nate dallo studio dei triangoli, sono periodiche, cioè si ripetono uguali a intervalli uguali. Per esempio, se si ‘percorre’ più volte la circonferenza, a ogni giro i valori del seno si ripetono uguali con una determinata frequenza e si ottiene una curva, detta sinusoide (v. fig.).
Molti sono i fenomeni naturali periodici: il più evidente è la rotazione terrestre che permette di scandire i giorni in periodi di 24 ore. Per tale motivo, le funzioni goniometriche sono utilizzate per descrivere fenomeni fisici che presentano oscillazioni ondulatorie periodiche (onde e oscillazioni), per esempio i segnali elettromagnetici attraverso i quali si diffondono informazioni via radio e televisione.
Anche il suono si produce attraverso oscillazioni periodiche dell’aria: è oscillando che la corda di una chitarra emette un suono, che può avere minore o maggiore volume o produrre una nota di diversa altezza (v. fig.).
Dal punto di vista fisico ciò corrisponde a funzioni periodiche di ampiezze o frequenze diverse.