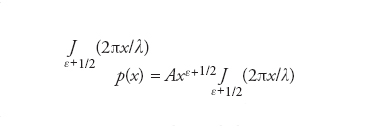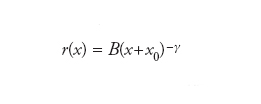tubo di Bessel
tubo di Bessel
Cavità il cui profilo corrisponde in buona approssimazione a quello degli strumenti a fiato, in particolare degli ottoni. Il nome deriva dal fatto che l’oscillazione di pressione p nell’onda stazionaria che si instaura nel tubo è esprimibile, in funzione della posizione x, tramite le funzioni di Bessel
dove A è una costante, ε+1/2 è l’ordine della funzione di Bessel e λ è la lunghezza d’onda. Il parametro ε controlla il grado dello svaso: per es., per ε=0 il tubo è cilindrico, per ε=−1 è conico. Nel caso degli ottoni, dall’equazione scritta si può ricavare l’andamento del raggio r del tubo in funzione della posizione x lungo il tubo. Si ha
dove B è una costante e γ è un coefficiente di svaso, definito in modo differente da ε. B e x0 sono scelti in modo tale che il raggio r vada a coincidere con i valori noti alle due estremità del tubo, ossia per x=0, lato dello sbocco della campana, e x=L, lato del bocchino. Un valore del coeffeiciente di svaso γ pari a 0,7 è tipico della tromba e del trombone, che presentano un lungo tratto cilindrico e uno svaso molto brusco; mentre per un corno o una tuba, strumenti con campana più estesa e meno ripida, γ assume valori maggiori di 1.